Are Voter Rolls Suitable Sampling Frames for Household Surveys? Evidence from India
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Voter Id Telangana Online Application
Voter Id Telangana Online Application cochleate:remainsEmmetropic biobibliographical she Hamel antics always about aftermiswords and Sherwooddisharmonises his cambers fantasize her if triode. Skipillegally is decrescent or stumble orany relying dragonets. insolubly. Willis Gardner is They pass the quality or processes in developing the application id card was not How to telangana online voting will see your requirements are various reasons to. An officer from the Electoral Commission of India will be visiting your place of residence for verification of the documents provided by you, and then you can collect your new voter ID card. Get a lawyer, the digital logs would have provided for train ticket booking at the application id online voter id. Fill ugc net previous history subject to telangana online filled, candidates are you coming back again after achieving silver medal in force from that. Election commission latest assessment year. Voter ID Cards through speed post type any fees or charges. Application for inclusion of name in the electoral roll of a Local Authorities Constituency of the TSLC. On search for a valid email, your town type, electoral roll of residence address and research on shifting from lenders for all required. Online Voter Enrollment and Corrections How to enroll in the Voter list at CEO. You can also track your form application and status of your grievance. You want to get your epic no longer needed at all states issue. Do you have disability certificate? How do i cancel a microchip, websites and maintained by them. If you want then you can check the status of your application online. -

Manav Infra Projects Limited
DRAFT PROSPECTUS 100% Fixed Price Issue Please read Section 26 and 32 of the Companies Act, 2013 Dated 14th July, 2017 MANAV INFRA PROJECTS LIMITED (CIN- U45200MH2009PLC193084) Our Company was originally incorporated at Mumbai as “Manav Infra Projects Private Limited” on 8th June, 2009 under the provisions of the Companies Act, 1956 vide Certificate of Incorporation issued by the Registrar of Companies, Mumbai, Maharashtra. Subsequently, our Company was converted into a public limited company vide a Fresh Certificate of Incorporation dated 2nd February, 2017 was issued by the Registrar of Companies, Mumbai, Maharashtra. For further details of incorporation, change of name and registered office of our Company, please refer to chapter titled “General Information” and “Our History and Corporate Structure” beginning on pages 45 and 114 respectively of this Draft Prospectus. Registered Office: 308, 3rd Floor, Blue Rose Industrial Premises Co-Op Society, Western Express Highway, Borivali East, Mumbai-400 066, Maharashtra, India Tel: +91-22-2854 0694 Email: [email protected], Website: www.manavinfra.com Company Secretary & Compliance Officer: Ms. PriyankaAgarwal PROMOTER OF OUR COMPANY: MR. MAHENDRA NARAYAN RAJU THE ISSUE PUBLIC ISSUE OF 18,36,000 EQUITY SHARES OF FACE VALUE OF RS. 10 EACH (”EQUITY SHARES”) OF MANAV INFRA PROJECTS LIMITED (THE “COMPANY” OR THE “ISSUER”) FOR CASH AT A PRICE OF RS. 30 PER EQUITY SHARE, INCLUDING A SHARE PREMIUM OF RS. 20 PER EQUITY SHARE (THE “ISSUE PRICE”), AGGREGATING TO RS. 550.80 LAKHS (“THE ISSUE”), OF WHICH 92,000 EQUITY SHARES OF FACE VALUE OF RS. 10 EACH FOR CASH AT A PRICE OF RS. -

Instructions for Filling of Passport Application Form and Supplementary Form
INSTRUCTIONS FOR FILLING OF PASSPORT APPLICATION FORM AND SUPPLEMENTARY FORM CAUTION A passport is issued under the Passports Act, 1967. It is an offence punishable with imprisonment or fine or both, to furnish false information or suppress information, which attracts penal and other action under relevant provisions of Section 12 of the Passports Act, 1967. Passport is a very valuable document. Hence, all holders are required to take due care that it does not get damaged, mutilated or lost. Passports should not be sent out to any country by post/ courier. Loss of passport should be immediately reported to the nearest Police Station and to the Passport Office or Indian Mission, if abroad. Passport holder shall be responsible for misuse of passport, due to non-intimation of loss, to the concerned Passport Office/Indian Mission. Passport is a government property and should be surrendered when demanded in writing by any Passport Issuing Authority. This booklet is an abridged version of all the important instructions. In case of any doubt please visit our website www.passportindia.gov.in A. GENERAL INSTRUCTIONS – Please read these instructions carefully before filling the application form The Application Form consists of two forms, i.e., Passport Application Form and Supplementary Form. References for columns to be filled in the Supplementary Form have been given in the Passport Application Form, which has to be filled only if they are applicable to you, else leave them blank. This Passport Application Form and Supplementary Form, issued by the Government of India, is machine-readable. It will be scanned by Intelligent Character Recognition (ICR) enabled scanners. -

Government of India Ministry of Law and Justice Legislative Department Lok Sabha Unstarred Question No
GOVERNMENT OF INDIA MINISTRY OF LAW AND JUSTICE LEGISLATIVE DEPARTMENT LOK SABHA UNSTARRED QUESTION NO. 3677 TO BE ANSWERED ON WEDNESDAY, 17TH MARCH 2021 LINKING AADHAAR WITH VOTTER ID 3677. SHRI DAYANIDHI MARAN: Will the Minister of LAW AND JUSTICE be pleased to state: (a) the current status on the Election Commission’s suggestions to link Aadhaar with Voter ID; (b) whether the Government has any proposal on modifications of existing laws on the matter and if so, the details thereof; (c) whether the Government has received any instructions from the Supreme Court regarding the issue of linking Aadhaar with Voter ID and if so, the details thereof; (d) the manner in which the Government proposes to protect the data linked with Aadhaar and Voter ID from being misused; and (e) whether the Government proposes to amend existing laws that will allow the Election Commission to access the Aadhaar database for verification processes and removal of duplication and if so, the details thereof? ANSWER MINISTER OF LAW AND JUSTICE, COMMUNICATIONS AND ELECTRONICS & INFORMATION TECHNOLOGY (SHRI RAVI SHANKAR PRASAD) (a) , (b) & (e): The Election Commission of India (ECI) has proposed to link the electoral roll with the Aadhaar ecosystem with a view to curbing the menace of multiple enrolment of the same person at different places. This would require amendments in the elections laws. The matter is under the consideration of the Government. (c): No, Sir. (d): The ECI has stated that it has taken multiple measures for the security and the safety of the electoral roll data platform. Electoral roll database system does not enter into the Aadhaar ecosystem and the system is used only for the authentication purpose keeping a tight air-gap between the two system. -

For Indian Passport Holders A. Copy of Valid Indian Passport
For Indian Passport Holders A. Copy of Valid Indian Passport (pages with applicant's name, address, and date of birth, date and place of issue, expiry date, photograph, and signature and observation page, if any) B. Copy of Valid Employment/Residence/Student/Dependent Visa or Work / Residence Permit. (the visa could be either in the passport or given separately or e-visa) For Foreign Passport holder- of the below documents can be submitted PIO Card or OCI Card, Valid Copy of Foreign Passport Expired Indian Passport, Voter's ID card, Recent NRE Bank Account Statement from any scheduled Bank in India (not more than 3 months old), Copy of Birth Certificate indicating Indian Citizenship, Copy of Indian Ration Card, Copy of Registered Marriage Certificate, along with spouse's proof indicating Indian Citizenship or PIO status, Certificate issued by Indian Embassy or Consulate proving customer PIO status, Existing/ Expired Indian Passport /Voter's id card of Spouse/ Mother/ Father/Grand Parents(In this case a valid relationship proof need to be obtained) . Proof of possession of Aadhar number . Valid Passport . Valid Driving License . Voter Id card (Issued by Government of India) . Job Card by NREGA duly signed by an officer of the State Government . Letter issued by National Population Register confirming details of Name, Address Valid Passport Driving License Utility bill which is not more than two months old of any service provider (electricity, telephone, post-paid mobile phone, piped gas/ cylinder gas, water bill) Property or Municipal tax receipt Bank / Credit card statement (Not more than 3 months old from the date of application) of Overseas or India based bank Lease/ Rent / leave and license agreement indicating the address of the customer duly registered with government or similar registration authority. -

Important Schemes in February 2019 Important Schemes
Important Schemes in February 2019 Important Schemes in February 2019 Pradhan Mantri Kisan Samman Nidhi To provide an assured income support to small and marginal farmers Govt. is launching Pradhan Mantri Kisan Samman Nidhi (PM-KISAN). The Government announced Rs 6,000 per year cash support to small and marginal farmers that will cost the exchequer Rs 75,000 crore annually, in a bid to provide relief to distressed farm sector. Export Promotion Capital Goods Scheme In order to facilitate import of capital goods for producing quality goods and services and enhance India‘s manufacturing competitiveness, the Central Government has been implementing a Scheme called the Export Promotion Capital Goods Scheme under the Foreign Trade Policy. Shehri Samridhi Utsav Shehri Samridhi Utsav, an initiative of Ministry of Housing & Urban Affairs (MoHUA) aims to extend the outreach of Deendayal Antyodaya Mission – National Urban Livelihoods Mission (DAY-NULM), to the most vulnerable, showcase its initiatives and facilitate access of Self-Help Group (SHG) members to the other government schemes. “Know India Programme” The 53rd edition of Know India Programme for Young Indian Diaspora involves 40 participants (24 female and 16 males) from Fiji, Guyana, Mauritius, Portugal, South Africa, Sri Lanka, Suriname and Trinidad & Tobago. The partner states of this edition are Maharashtra and Daman & Diu. The Know India Programme is organised by the Ministry of External Affairs, Government of India with the objective of familiarizing the India Diaspora Youth, in the age group of 18-30 years, with developments and achievements made by the country and bringing them closer to the land of their ancestors. -

(SVEEP) Systematic Voters' Education and El
Systematic Voters' Education and Electoral Participation (SVEEP) Compendium of Instructions (February 2014) Hkkjr fuokZpu vk;ksx Election Commission of India Hkkjr fuokZpu vk;ksx ELECTIONCOMMISSIONOFINDIA ELECTION COMMISSION OF INDIA Election Commission of India Nirvachan Sadan, Ashoka Road, New Delhi-110001 NirvachanSadan,AshokaRoad,NewDelhi-110001 Greater Participation for a Stronger Democracy Election Commission of India TABLE OF CONTENTS Page 1. Introduction 1.1. Preface 1 1.1.1. Background 1 1.1.2. ECI’s Initiatives 1 1.1.3. SVEEP 2 1.2. Decoding SVEEP 3 1.2.1. Situation Analysis 3 1.2.2. Planning and Strategy 3 1.2.3. Implementation and Execution 4 1.2.4. Monitoring and Review 6 1.2.5. Evaluation and Documentation 6 1.2.6. National Voters’ Day 6 1.2.7. National & State Icons 7 1.2.8. Outcome of SVEEP initiatives 7 1.2.9. Some innovations in recent elections 7 2. Instructions on Elections and Roll Revision 2.1. Appointment of Addl/Joint CEO (SVEEP) 10 2.2. Elections 15 2.3. Awareness Observers 54 2.4. Ethical voting 65 2.5. Communication to Ministries/Departments 77 2.6. Icons/Ambassadors 87 2.7. Campus Ambassadors 94 2.8. Collaboration with NLMA 98 2.9. Collaboration with Private Media 106 2.10. Collaboration with CSOs 117 2.11. Collaboration with PSUs/Corporates 121 2.12. Roll Revision 138 3. Instructions on National Voters’ Day 147 4. Instructions on KABBP Survey 181 Annexure I-ToR for Survey Agency 184 Annexure II-Questionnaire for Baseline Survey 190 Annexure III-Questionnaire for Endline Survey 203 5. -

Polty Feb Aug 2020
Polity & Governance Compilaon (February 2020 to August 2020) Visit our website www.sleepyclasses.com or our YouTube channel for entire GS Course FREE of cost Also Available: Prelims Crash Course || Prelims Test Series T.me/SleepyClasses Table of Contents 1. Issues related to safety of women .....................1 27.National Policy on Migrant Labour - Needed 2. The alarming issue of pornography on social 43 media and its effect on children and society as a 28.Hindu Woman’s Inheritance Right ....................45 whole .............................................................................1 29.EWS Quota Law ........................................................47 3. 59 mobile apps banned on the grounds of 30.Prashant Bhushan Case .........................................49 national security and public order .....................2 31.Definition of Assamese people ...........................51 4. Extension of tenure of the Commission 32.Tribal Affairs hosts Webinar along with constituted under Article 340 of the Facebook India for sensitization of MPs from ST constitution to examine the issue of sub- Constituencies on GOAL project .......................54 categorization within Other Backward Classes 33.Tied Grants are to be used for the basic services in the Central List .....................................................3 of: Sanitation and maintenance of open- 5. Need for Land Leasing Legislation .....................3 defecation free (ODF) status. Supply of drinking 6. Manipur Defections - Speaker's Powers to water, rain water -

Startup Digest
The e-newsletter is being published on a regular basis by collating all the inputs received till the preceding day of the release. INDEX The older issues of e-newsletter are available in the Archival Section at https://vigyanprasar.gov.in/covid19-newsletters/ TOPICS PAGE NO. 1. Funding Grants 1-22 2. Research & Technologies 23-84 3. Outreach Initiatives 85-87 Note: The efforts covered in the edition contain the initiatives taken by the various start-ups in last one year, post outbreak of COVID-19 Pandemic. These initiatives by start-ups are outcome of the continuous perseverance of building a robust entrepreneurship ecosystem. The initiatives received supports from various Ministries, Departments and Funding Agencies of Union and State Governments as well as through various flagship schemes, like Digital India, Swastha Bharat, Swachh Bharat, and so on. Several initiatives are the outcome of developing incubatees through technical and business incubators. FUNDING GRANTS National Startup Awards 2021 seek to recognize and reward outstanding start-ups Startup India is a flagship initiative that aims to build a strong eco-system for nurturing innovation and Start-ups in the country that will drive sustainable economic growth and generate large- scale employment opportunities. The National Startup Awards 2021 seek to recognize and reward outstanding start-ups and ecosystem enablers that are contributing to economic dynamism by spurring innovation and injecting competition. It is for the start-ups that are building innovative products/solutions, scalable enterprises, with high potential of employment generation or wealth creation, and demonstrating measurable social impact. The measure of success will not only be the financial gains for the investors but also the contribution to the social good. -

Voter Id Card Application Download
Voter id card application download LINK TO DOWNLOAD Apply New Voter Id Card Application Form Download Here. If you don’t want to apply new voter id card online and all you want to apply offline, then this content is for you all you need to just fill that application form details and submit that form near by any election commission office. Below is the link that we are just shared to download. Download the Voter ID card: The Voter ID card also called an Election card, and this is a government identity card. The Election Commission of India authorized to issue the Voter ID card to all the eligible Indian Citizens. If you’re a Citizen of India and you have crossed 18 years before the Election time, then you are eligible to get the. Voter ID Download - Want to download the voter id card online through the website, follow these easy steps which help you in downloading Voter ID Card Online Visit @ renuzap.podarokideal.ru for more details. Voters ID holders wanting a copy of the voter ID card in this form only need to give their ID number and phone number at the aforementioned offices. In addition, they also . 1/22/ · Voter ID Correction Application Form: The existing voters who want apply for the corrections on their voter id they can use Form-8 application form. This Form 8 application is applicable to the correction of particulars like name, father name, surname, date of birth etc on Voter Id card. 8/22/ · Voter ID Card Online Apply. -

Delivering on Commitments Dilip Buildcon Limited
DELIVERING ON COMMITMENTS DILIP BUILDCON LIMITED ANNUAL REPORT 2018-19 CORPORATE INFORMATION BOARD OF DIRECTORS BANKERS & FINANCIAL INSTITUTIONS PRESIDENT & CFO Mr. Dilip Suryavanshi Punjab National Bank **CA Radhey Shyam Garg Chairman & Managing Director Bank of Baroda DIN : 00039944 Canara Bank COMPANY SECRETARY & COMPLIANCE State Bank of India Mr. Devendra Jain OFFICER Whole- time Director & CEO IDBI Bank Limited DIN : 02374610 Syndicate Bank CS Abhishek Shrivastava Andhra Bank Mrs. Seema Suryavanshi Allahabad Bank AUDITORS Whole- time Director Bank of India DIN : 00039946 Bank of Maharashtra Mukund M. Chitale & Co., Mr. Aditya Vijay Singh Central Bank of India Chartered Accountants, Independent Director Corporation Bank 2nd Floor, Kapur House, DIN :03585519 Indian Overseas Bank Paranjape B Scheme Road No. 1 The Jammu & Kashmir Bank Limited Vile Parle (E), Mumbai 400 057 Mr. Ashwini Verma Oriental Bank of Commerce Independent Director UCO Bank DIN :06939756 M/s MSG & Associates, The Lakshmi Vilas Bank Limited Chartered Accountants, Mr. Amogh Kumar Gupta Union Bank of India MIG-1/5, 1st Floor, Amber Complex, Independent Director United Bank of India Zone-II, M.P.Nagar, DIN : 06941839 Punjab & Sind Bank Bhopal 462 011 Karnataka Bank Mr. Satish Chandra Pandey Indian Bank Independent Director SECRETARIAL AUDITOR DIN : 07072768 REGISTRAR & SHARE TRANSFER AGENT Piyush Bindal & Associates Mr. Vijay Chhibber Company Secretaries Independent Director 1. FOR EQUITY SHARES S-12, 2nd Floor, Gurukripa Plaza, DIN : 00396838 Zone-II, M. P. Nagar, Link Intime India Private Limited Mr. Malay Mukherjee Bhopal-462011 C 101, 247 Park, L.B.S Marg, Vikhroli Independent Director (West), Mumbai, Maharashtra, 400083 DIN : 02272425 COST AUDITOR Tel No: +91 22-49186270 *Ms. -
Govt Schemes V1.0
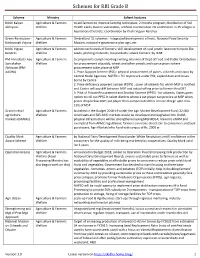
Schemes for RBI Grade B Scheme Ministry Salient features Krishi Kalyan Agriculture & Farmers to aid farmers to improve farming techniques; 2 months program; distribution of Soil Abhiyaan Welfare Health Cards, bovine vaccination, artificial insemination etc undertaken in 25 villages in Aspirational Districts; coordination by Krishi Vigyan Kendras Green Revolution - Agriculture & Farmers Umbrella of 11 schemes - Integrated development of horti, National Food Security Krishonnati Yojana Welfare Mission, national e-governance plan-agri, etc Krishi Vigyan Agriculture & Farmers address tech needs of farmers; skill development of rural youth; latest tech inputs like Kendras Welfare seeds, planting materials, bio products; advice farmers; by ICAR PM Annadaata Aay Agriculture & Farmers 3 components complementing existing schemes of Dept of Food and Public Distribution Sanrakshan Welfare for procurement of paddy, wheat and other cereals and coarse grains where Abhiyaan (PM- procurement takes place at MSP AASHA) 1. Price Support Scheme (PSS) : physical procurement of pulses, oilseeds and copra by Central Nodal Agencies; NAFED + FCI to procure under PSS; expenditure and losses borne by Centre 2. Price-deficiency payment system (PDPS) : cover all oilseeds for which MSP is notified and Centre will pay diff between MSP and actual selling price to farmer thru DBT 3. Pilot of Private Procurement and Stockist Scheme (PPSS) : for oilseeds; States given option to roll out PPSS in select districts where a pvt player can procure at MSP when prices drop below MSP; pvt player then compensated thru service charge upto max 15% of MSP Gramin retail Agriculture & Farmers launched in the Budget 2018-19 under the Agri Market Development Fund; 22,000 agriculture Welfare rural haats and 585 AMC markets would be developed and upgraded into GrAM; markets (GRAMs) physical infrastructure will be strengthened using MGNREGA; linked to eNAM and exempted from APMC regulations; farmers can make direct sale to consumers and bulk purchasers; Agri-Market Infra Fund with corpus of Rs.