DOCSLIB.ORG

Geometrical Frustration in Ising Magnets

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geometrical Frustration in Ising Magnets ��������������������������� ����� ������������������������ KAM Collaborators: M. Khatun (Ball State) J. Barry (UF) ����������������������� AF AF AF AF AF AF AF HAPPY ! FRUSTRATED !! Geometry determines if lowest energy state for each bond can be satisfied. Leads to large ground state degeneracy Leads to disordered ground states (e.g. spin-­liquids) ����������������������� Figures from Wikipedia Triangles in 2D Tetrahedrons in 3D Can be present in different types of lattices in 2D or 3D ����������������������� Figures from Wikipedia AF FM Spins along easy axes Frustrated spins Zero moment with AF interactions with FM interactions Frustration can be for ferro or antiferromagnetic interactions ��������������������������������� ��������� Giauque and Stout (1936) Residual entropy Estimated from expt 185.3 J/(mol.K) Compare with theory Ideal gas 188.7 J/(mol.K) Missing entropy: 3.4 J/(mol.K) Pauling: configurational entropy 푁푘 ln 3/2 = 3.4 J/(mol.K) !! 퐵 Ramirez (1994) site disordered Ramirez (1994) site ordered ����� ������������������������������ �������� 2D triangular kagomé 푧 푧 퐻=−퐽 2 5 σ 푖σ 푗 :;,=> Both have disordered ground states with finite residual entropy 푆 0 = 0.3231 Triangular Ising Antiferromagnet (TIA) 푁푘퐵 = 0.5018 Kagomé Ising Antiferromagnet (KIA) Is residual entropy a good measure of the degree of frustration? �������������������������� Usable Power: Ramirez: 1994 Θ퐶푊 Empirical measure of frustration: 푓=− 푇푁 Ramirez (1994) ���������������������������������������� Add field parallel to Ising spin axis: −ℎ 5 σ푧 ⇒ χ 푖 ⎪⎪ ; perpendicular to Ising spin axis: −ℎ 5 σ푥 ⇒ χ 푖 ⊥ ; ↑ ��������������������������� χ χ Both ⎪⎪ and ⊥ can be expressed in terms of spin-­correlations. χ ⎪⎪ requires knowledge of pair correlations at all distances. χ ⊥ requires knowledge of finite number of local pair and multi-­spin correlations ������� • Will consider two exactly solvable models (1) Kagome Ising Antiferromagnet (KIA), with strong geometrical frustration. (2) A triplet interaction model (KIA-­‐T) with no frustration. • For KIA: Obtain χ ⊥ exactly for all temperature and χ accurately at high temperatures. ⎪⎪ • For KIA-­‐T: Obtain χ and χ as well as entropy ⊥ ⎪⎪ exactly at all temperatures Propose a quantitative measure of the degree of frustration ������������ ��������������� ����� 푧 푧 퐻=−퐽 2 5 σ 푖σ 푗 :;,=> ���������������������������������������������� ��������������������������� Barry and Khatun: 1987 JKLM [O∑V Q T] 2 WSXY RS ] 휒 =푚 훽푁 V ; 푄= 훽퐽; 훽≡ ⊥ O ∑ Q T ^ ` WSXY RS _ m: magnetic moment q: number of nearest neighbors Sum is over all nearest neighbors �����χ⊥ ����������������������������� 휒 + − ⊥a0 =푞 푄 [퐴 +2퐴0(푥 +푥 +푥 ) +퐴 푥 ] 휒2 2 01 05 06 1234 푚2 1 tanh4푄 tanh2푄 0 퐴 ±≡ 2 ± 4 2 + 3 휒2 ≡ 푞|퐽2| 8 4푄2 2푄2 1 tanh4푄 퐴0 ≡ 2 −1 8 4푄2 푧 푧 푥푖푗 ≡ σ 푖σ 푗 ≡ 푖푗 푧 푧 푧 푧 푥1234 ≡ σ 1σ 2σ 3σ 4 ≡ 1234 Need pair correlations <01>, <05>, <06> and quartet correlation <1234> ��������������������� Barry and Khatun (1997);; KAM, Khatun and Barry (unpublished) = kBT/4J2 Note: pair correlations at distances farther apart decay faster with temperature ���������������������������� KAM, Khatun and Barry (2017, unpublished) = kBT/4J2 Note: The zero temperature limit corresponds to a 1/T divergence with an amplitude smaller than 1 (~ 0.4458) ���������������������������� 퐾퐼퐴 2 푧 푧 Need pair correlations at all 휒 푇=푚 훽 5 σ0 σ푖 0 ∥ distances. Only six are known ; 휒 퐾퐼퐴 ∥ a 0 = 푞훽퐽 [1 + 4 01 + 4 05 + 2 15 + 4 06 휒2 2 + 8 16 + 4 26 + …..] Strategy: Compare results with four-­, five-­ and six-­pairs How much do the results change? �������������������������������������� 1/|4Q2|= kBT/4J2 th Adding 6 pair changes result by 0.006% at 1/|4Q 2| ~ 10 and by 0.0002% at 1/|4Q 2| ~ 30. Thus high-­T limit is essentially exact. Extrapolation gives Θ퐶푊= 4J2/kB ;; agrees with high-­T expansion �������������� ���������������������� • Perpendicular susceptibility diverges as c/T, as T goes to zero, with c <1. Follows 1/T at large T. Compare free spins: c=1 • Parallel susceptibility could not be calculated exactly at low-­T limit. Follows Curie-­Weiss law 1/(T-­Θ 퐶푊) at large T with Θ퐶푊= 4J2/kB <0. Agrees with high temperature expansion results. Compare free spins: Θ 퐶푊= 0. Is any of these a good measure of geometrical frustration? Compare with another exactly solvable model on kagome lattice that has no geometrical frustration �������������������������������� 푧 푧 푧 퐻푡푟푖푝푙푒푡 =−퐽 3 5 σ 푖σ 푗σ 푘 :;=^> 2D kagome All spins are `satisfied’;; flipping any one would + increase energy + -­‐ No frustration �������������������������������� ��� ������������������������������������� ������� 푧 푧 푧 퐻푡푟푖푝푙푒푡 =−퐽 3 5 σ 푖σ 푗σ 푘 :;=^> 2D kagome 푧 푧 푧 푧 퐻푞푢푎푟푡푒푡 =−퐽 4 5 σ 푖σ 푗σ 푘 σ 푙 :;=^x> Barry and Wu (1989) 3D pyrochlore ������������������������ Both triplet and quartet models belong to a class of multi-­spin (cluster) interactions of `only one kind’ whose partition functions Z are exactly calculable. Diagrammatic expansion of Z in powers of tanh Q in the thermodynamic limit has contribution only when the path length is zero (no finite length path consisting exclusively of basic interaction clusters can totally close upon itself). Barry and Wu (1989) used graph theory to show that in the quartet interaction model, only two terms survive in Z due to the corner-­sharing nature of the 3D pyrochlore lattice corresponding to two complementary graphs. Because 2D kagome has corner sharing triangles, it is possible to adapt the same techniques. ��������������������������������� O ∑| { { { 푍푁 =5푒 z ; = ^ { = cosh푄 2푁/3 5€ 1 +휎 휎 휎 tanh 푄 3 푖 푗 푘 3 ‚{ 2푁/32푁 2푁/3 = cosh푄 3 [1 + (tanh푄 3) ] Differs from the quartet model only by the exponent 2N/3 The magnetic Helmholtz free energy per spin is 1 2/3 훽푓 푄3 = lim ln푍 푁 푄3 = ln [2(cosh푄3) …→‡푁 ������������������������������������� tanh [푄 휎 휎 +휎 휎 ] 휒 =푚 2훽 3 1 2 3 4 ⊥ 푄3(휎1휎2 +휎 3휎4) tanh [푄3 휎1휎2 +휎 3휎4 ] + − =퐵 + 퐵 휎1휎2휎3휎4 푄3(휎1휎2 +휎 3휎4) 1 tanh 2푄 퐵± = 3 ± 1 2 2푄3 Thermal average of the “bow-­tie” unit 1 O ∑ { { { 휎 휎 휎 휎 = 5 휎 휎 휎 휎 푒 z | ; = ^ 1 2 3 4 1 2 3 4 푍푁 { 1 2푁/3 = cosh푄 3 5 휎1휎2휎3휎4 € 1 +휎 푖휎푗휎푘 tanh푄 3 푍푁 { ‚ Graph theory: only two terms in the sum survive! ������������������������������������������� 2 휎1휎2휎3휎4 = tanh Q3 휒 퐾퐼퐴푇 푞 ⊥ a0 = 푄 1−tanh 2 푄 + tanh |푄 | 휒3 2 3 3 3 푚2 0 휒3 ≡ 푞퐽3 �������������������������������������� All pair correlations of KIA-­T vanish, giving 휒 퐾퐼퐴푇 4퐽 ∥ 3 0 = 휒3 푘퐵푇 ������χ ����χ �������� ⎪⎪ ⊥ = kBT/4|J3| Contrast with KIA: Absence of 1/T divergence of χ⊥ at T=0 and zero intercept of (χ )-­‐1 implying Θ = 0. ⎪⎪ 퐶푊 ���������������������� 휕 푆 = 푘퐵 1−훽 ln푍 푁 휕훽 푁 In the thermodynamic limit N→ 0, 푆퐾퐼퐴푇 2 = ln2 + [ln (cosh푄3)−푄 3 tanh 3 푄 ] 푁푘퐵 3 KIA-­T Finite residual entropy S 0 /NkB = (ln 2)/3 = 0.2310 …. KIA Compare: S 0 /NkB = 0.5018 TIA S0 /NkB = 0.3231 Example of large ground state degeneracy but zero frustration ������������������������ • Perpendicular susceptibility remains finite as T goes to zero. Follows 1/T at large T. Compare KIA: 휒 diverges as T goes to zero ⊥ • Parallel susceptibility follows Curie-­Weiss law 1/T with Θ퐶푊=0. Compare KIA: Θ 퐶푊 < 0. • Residual entropy finite: 0.2310 NkB (has no frustration) Compare KIA: 0.5018 NkB (has large frustration) ��������������������������������� • KIA is highly frustrated, but KIA-­T has no geometrical frustration. This implies the following: • Residual entropy can not be a measure of geometrical frustration. Compare finite S 0 for both KIA and KIA-­T. • Curie-­Weiss temperature Θ퐶푊 is finite for frustrated KIA but zero for unfrustrated KIAT • Perpendicular susceptibility diverges for KIA but remains finite for KIA-­T. Compare with other available exact results ������������������������������ Wannier (1950);; Houtappel (1950);; Kano and Naya (1953);; Sykes and Zucker (1961);; Stephenson (1964);; Barry and Khatun (1987) • TIA is the Triangular Ising Antiferromagnet and KIF is the Kagome Ising Ferromagnet. • TIA highly frustrated, KIF is not frustrated. • TIA remains disordered down to zero temperature, KIF orders at a finite Tc. • Residual entropy of TIA is 0.3231. It is zero for KIF. •Θ 퐶푊 is positive for KIF and negative for TIA. • Perpendicular susceptibility diverges for TIA but remains finite for KIF. �������������η(T) 푘 푇 η 푇 ≡ 퐵 휒 (푇) η ≡ η(푇 → 0) 푚2 ⊥ 0 Consider four different Ising models: (1) KIA: strong geometric frustration, disordered ground state, finite residual entropy (2) KIA-­T: no geometrical frustration disordered ground state, finite residual entropy (3) KIF: no geometrical frustration ordered ground state, zero residual entropy (4) TIA: strong geometrical frustration disordered ground state, finite residual entropy ��������������������� η0 KIA: 0.4458 TIA: 0.2900 KIA-­T: 0 KIF: 0 Proposal: η0 is a measure of degree of frustration �������� • Considered two exactly solvable models, KIA and KIA-­T • Obtained exact χ ⊥(T) and accurate ΘCW for KIA • Obtained exact χ (T), χ (T) and entropy S(T) for KIA-­T ⊥ ⎪⎪ • Comparing the results with known results for KIF and TIA leads to the proposal that η 0 is a good quantitative measure of geometrical frustration. • Different zero temperature limits of χ (T) and χ (T) ⊥ ⎪⎪ imply different types of degenerate states. ������� •A finite residual entropy implies large ground state degeneracy for both KIA and KIA-­T, but the nature of low-­energy excitations must be very different since one has large geometrical frustration but the other has none. • This difference shows up in the zero temperature limit of the perpendicular susceptibility. • In a more general case with both pair and triplet interactions simultaneously present , the interplay of disorder with and without frustration might lead to more interesting possibilities. • This is not just a mathematical curiosity. Presence of weak triplet interaction in addition to a dominant pair interaction is actually quite ubiquitous in nature. �����������.
Load more

Recommended publications
  • Introduction to Frustrated Magnetism
    Springer Series in Solid-State Sciences 164 Introduction to Frustrated Magnetism Materials, Experiments, Theory Bearbeitet von Claudine Lacroix, Philippe Mendels, Frédéric Mila 1. Auflage 2011. Buch. xxvi, 682 S. Hardcover ISBN 978 3 642 10588 3 Format (B x L): 15,5 x 23,5 cm Gewicht: 1339 g Weitere Fachgebiete > Physik, Astronomie > Elektrodynakmik, Optik > Magnetismus Zu Inhaltsverzeichnis schnell und portofrei erhältlich bei Die Online-Fachbuchhandlung beck-shop.de ist spezialisiert auf Fachbücher, insbesondere Recht, Steuern und Wirtschaft. Im Sortiment finden Sie alle Medien (Bücher, Zeitschriften, CDs, eBooks, etc.) aller Verlage. Ergänzt wird das Programm durch Services wie Neuerscheinungsdienst oder Zusammenstellungen von Büchern zu Sonderpreisen. Der Shop führt mehr als 8 Millionen Produkte. Chapter 1 Geometrically Frustrated Antiferromagnets: Statistical Mechanics and Dynamics John T. Chalker Abstract These lecture notes provide a simple overview of the physics of geomet- rically frustrated magnets. The emphasis is on classical and semiclassical treatments of the statistical mechanics and dynamics of frustrated Heisenberg models, and on the ways in which the results provide an understanding of some of the main observed properties of these systems. 1.1 Introduction This chapter is intended to give an introduction to the theory of thermal fluctua- tions and their consequences for static and dynamic correlations in geometrically frustrated antiferromagnets, focusing on the semiclassical limit, and to discuss how our theoretical understanding leads to an explanation of some of the main observed properties of these systems. A central theme will be the fact that simple, classi- cal models for highly frustrated magnets have a ground state degeneracy which is macroscopic, though accidental rather than a consequence of symmetries.
    [Show full text]
  • Geometrical Frustration, Phase Transitions and Dynamical Order
    Geometrical frustration, phase transitions and dynamical order The Tb2M2O7 compounds (M = Ti, Sn) Yann Chapuis PhD supervisor: Alain Yaouanc September 2009 Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 1 / 36 Outline 1 Introduction 2 The Tb2M2O7 compounds (M = Ti, Sn) 3 Tb2Ti2O7 : sample study 4 Crystal field levels 5 Conclusions Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 2 / 36 Outline 1 Introduction geometrical frustration connectivity and degeneracy spin ice 2 The Tb2M2O7 compounds (M = Ti, Sn) 3 Tb2Ti2O7 : sample study 4 Crystal field levels 5 Conclusions Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 3 / 36 Introduction geometrical frustration impossibility to satisfy simultaneously all the magnetic interactions frustration index : f = |θCW |/Tc ; frustration if f & 5 θCW : Curie-Weiss temperature Tc : transition temperature example of 2D Ising antiferromagnets Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 4 / 36 Introduction geometrical frustration triangular lattice Kagom´elattice garnet lattice pyrochlore lattice Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 5 / 36 Introduction connectivity and degeneracy low connectivity = large degeneracy Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 6 / 36 Introduction spin ice water ice (on the left) and spin ice (on the right) : analogy between protons displacement vectors and magnetic moments water ice = each oxygen with two protons close and two protons away (Pauling) spin ice = two spins in, two spins out → six equivalent configurations
    [Show full text]
  • Spin Glass Transitions in Geometrically Frustrated Magnets
    UNIVERSITY of CALIFORNIA SANTA CRUZ SPIN GLASS TRANSITIONS IN GEOMETRICALLY FRUSTRATED MAGNETS A thesis submitted in the partial satisfaction of the requirements for the degree of BACHELOR OF SCIENCE in APPLIED PHYSICS by CHRIS KINNEY 8 FEBRUARY 2016 The thesis of Chris Kinney is approved by Professor Arthur Ramirez Professor David Belanger Technical Advisor Thesis Advisor Professor Robert Johnson Chair, Department of Physics 0 Table of Contents Abstract……………………………………………………………………………...……………………………………………………………(2) Introduction………………………………………………………..…………………….……………………………………………………..(3) Data, Analysis and Methods……………………………………………………………………………………………………………..(6) Conclusion………………………………………………………………………………………………………………………………………(15) References………………………………………………………………………………………………………………………………………(16) 1 Abstract Spin glasses are magnetic systems exhibiting both quenched disorder and frustration, and have often been cited as examples of ‘complex systems.’ At the spin glass “freezing temperature” the spins stop fluctuating but do not exhibit long range orientational order. Geometrically frustrated magnets often exhibit spin glass behavior. In this paper spin glass physics is briefly discussed. We then discuss geometrically frustrated magnetism. This is followed by a discussion of experimental data taken in the lab on the magnetic freezing temperature of two different frustrated materials in various external magnetic fields. Two different known geometrically frustrated spin glass materials were cooled to helium temperatures. Magnetic moment data were collected
    [Show full text]
  • S41467-021-24636-1.Pdf
    ARTICLE https://doi.org/10.1038/s41467-021-24636-1 OPEN Dimensional reduction by geometrical frustration in a cubic antiferromagnet composed of tetrahedral clusters ✉ Ryutaro Okuma 1,2,7 , Maiko Kofu 3, Shinichiro Asai1, Maxim Avdeev 4,5, Akihiro Koda6, Hirotaka Okabe6, Masatoshi Hiraishi6, Soshi Takeshita 6, Kenji M. Kojima6,8, Ryosuke Kadono6, Takatsugu Masuda 1, Kenji Nakajima 3 & Zenji Hiroi 1 1234567890():,; Dimensionality is a critical factor in determining the properties of solids and is an apparent built- in character of the crystal structure. However, it can be an emergent and tunable property in geometrically frustrated spin systems. Here, we study the spin dynamics of the tetrahedral cluster antiferromagnet, pharmacosiderite, via muon spin resonance and neutron scattering. We find that the spin correlation exhibits a two-dimensional characteristic despite the isotropic connectivity of tetrahedral clusters made of spin 5/2 Fe3+ ions in the three-dimensional cubic crystal, which we ascribe to two-dimensionalisation by geometrical frustration based on spin wave calculations. Moreover, we suggest that even one-dimensionalisation occurs in the decoupled layers, generating low-energy and one-dimensional excitation modes, causing large spin fluctuation in the classical spin system. Pharmacosiderite facilitates studying the emergence of low-dimensionality and manipulating anisotropic responses arising from the dimensionality using an external magnetic field. 1 Institute for Solid State Physics, University of Tokyo, Kashiwa, Chiba, Japan. 2 Okinawa Institute of Science and Technology Graduate University, Onna, Okinawa, Japan. 3 Materials and Life Science Division, J-PARC Center, Japan Atomic Energy Agency, Tokai, Ibaraki, Japan. 4 Australian Nuclear Science and Technology Organisation, New Illawarra Road, Lucas Heights, Australia.
    [Show full text]
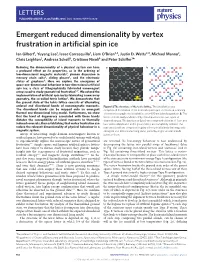
  • Emergent Reduced Dimensionality by Vertex Frustration in Artificial Spin
    LETTERS PUBLISHED ONLINE: 26 OCTOBER 2015 | DOI: 10.1038/NPHYS3520 Emergent reduced dimensionality by vertex frustration in artificial spin ice Ian Gilbert1, Yuyang Lao1, Isaac Carrasquillo1, Liam O’Brien2,3, Justin D. Watts2,4, Michael Manno2, Chris Leighton2, Andreas Scholl5, Cristiano Nisoli6 and Peter Schier1* Reducing the dimensionality of a physical system can have ab a profound eect on its properties, as in the ordering of low-dimensional magnetic materials1, phonon dispersion in mercury chain salts2, sliding phases3, and the electronic states of graphene4. Here we explore the emergence of quasi-one-dimensional behaviour in two-dimensional artificial spin ice, a class of lithographically fabricated nanomagnet arrays used to study geometrical frustration5–7. We extend the implementation of artificial spin ice by fabricating a new array 1 µm geometry, the so-called tetris lattice8. We demonstrate that the ground state of the tetris lattice consists of alternating ordered and disordered bands of nanomagnetic moments. Figure 1 | The structure of the tetris lattice. The tetris lattice is a The disordered bands can be mapped onto an emergent complicated decimation of the artificial square spin ice lattice. a, Scanning thermal one-dimensional Ising model. Furthermore, we show electron micrograph of a tetris lattice with 600 nm island separation. b, The that the level of degeneracy associated with these bands lattice is most easily understood by decomposition into two types of dictates the susceptibility of island moments to thermally diagonal stripes. The backbones (blue) are comprised of chains of four- and induced reversals, thus establishing that vertex frustration can two-vertex islands and, in the ground state, are completely ordered.
    [Show full text]
  • Resilience of the Topological Phases to Frustration Vanja Marić1,2, Fabio Franchini1, Domagoj Kuić1 & Salvatore Marco Giampaolo1*
    www.nature.com/scientificreports OPEN Resilience of the topological phases to frustration Vanja Marić1,2, Fabio Franchini1, Domagoj Kuić1 & Salvatore Marco Giampaolo1* Recently it was highlighted that one-dimensional antiferromagnetic spin models with frustrated boundary conditions, i.e. periodic boundary conditions in a ring with an odd number of elements, may show very peculiar behavior. Indeed the presence of frustrated boundary conditions can destroy the local magnetic orders presented by the models when diferent boundary conditions are taken into account and induce novel phase transitions. Motivated by these results, we analyze the efects of the introduction of frustrated boundary conditions on several models supporting (symmetry protected) topological orders, and compare our results with the ones obtained with diferent boundary conditions. None of the topological order phases analyzed are altered by this change. This observation leads naturally to the conjecture that topological phases of one-dimensional systems are in general not afected by topological frustration. Complex systems and their diferent ordered phases have always attracted a large interest, not only from a purely speculative point of view but also for the innumerable technological applications that exploit their characteristics1–3. In the middle of the last century, all the diferent phases of many-body systems obeying the laws of classical mechanics were classifed, using the Landau theory 4. According with this theory, diferent phases are characterized by diferent order parameters. Each one of them is uniquely associated to a particular kind of order that is related to the violation of a specifc symmetry (spontaneous symmetry breaking 5). It is therefore evident that, in the framework of Landau theory, the key role is played by the symmetries of the system, while other aspects, such as the boundary conditions, fall into the background and, generally, are considered not to be relevant for the presence or the absence of a particular kind of order.
    [Show full text]
  • Ordered Spin-Ice State in the Geometrically Frustrated Metallic-Ferromagnet Sm2mo2o7
    Ordered spin-ice state in the geometrically frustrated metallic-ferromagnet Sm2Mo2O7 Surjeet Singh1*, R. Suryanarayanan1, R. Tackett2, G. Lawes2, A. K. Sood3, P. Berthet1, 1 A. Revcolevschi 1Université Paris Sud, Laboratoire de Physico-Chimie de l'Etat Solide, UMR8182, Bât 414, Orsay, France. 2Department of Physics and Astronomy, Wayne State University, Detroit, MI 48202 USA. 3Department of Physics, Indian Institute of Science, Bangalore 560012, India. The recent discovery of Spin-ice is a spectacular example of non-coplanar spin arrangements that can arise in the pyrochlore A2B2O7 structure. We present magnetic and thermodynamic studies on the metallic-ferromagnet pyrochlore Sm2Mo2O7. Our studies, carried out on oriented crystals, suggest that the Sm spins have an ordered spin-ice ground state below about T* = 15 K. The temperature- and field-evolution of the ordered spin-ice state are governed by an antiferromagnetic coupling between the Sm and Mo spins. We propose that as a consequence of a robust feature of this coupling, the tetrahedra aligned with the external field adopt a “1-in, 3-out” spin structure as opposed to “3-in, 1-out” in dipolar spin ices, as the field exceeds a critical value. PACS: 75.30 –m, 75.30.Kz, 75.40Cx, 81.30-h Geometrical frustration arises when the magnetic interactions on a lattice are incompatible with the underlying crystalline symmetry. Systems with magnetic ions on triangular or tetrahedral lattices can exhibit geometrical frustration, which is often relieved at sufficiently low temperatures by weak residual interactions giving way to complex magnetic ground states1. One particularly important example of geometrical frustration arises in materials based on the pyrochlore structure (A2B2O7), where A and B ions form networks of corner-linked tetrahedra displaced by half the unit cell dimensions from each other.
    [Show full text]
  • Frustrated Spin Systems
    7 Frustrated Spin Systems Fred´ eric´ Mila Institute of Theoretical Physics Ecole Polytechnique Fed´ erale´ de Lausanne 1015 Lausanne, Switzerland Contents 1 Introduction 2 2 Competing interactions and degeneracy 3 2.1 Ising . 3 2.2 Heisenberg . 6 3 Classical ground-state correlations 8 3.1 Algebraic correlations . 8 3.2 Dipolar correlations . 10 4 Order by disorder 12 4.1 Quantum fluctuations . 12 4.2 Thermal fluctuations . 14 5 Alternatives to magnetic long-range order in Heisenberg models 14 5.1 Spin gap . 15 5.2 Resonating Valence Bond spin liquids . 17 5.3 Algebraic spin liquids . 21 5.4 Chiral spin liquids . 23 5.5 Nematic order . 24 6 Conclusion 27 E. Pavarini, E. Koch, and P. Coleman (eds.) Many-Body Physics: From Kondo to Hubbard Modeling and Simulation Vol. 5 Forschungszentrum Julich,¨ 2015, ISBN 978-3-95806-074-6 http://www.cond-mat.de/events/correl15 7.2 Fred´ eric´ Mila 1 Introduction In the field of magnetism, the word frustration was first introduced in the context of spin glasses to describe the impossibility of simultaneously satisfying all exchange processes. In this lec- ture, we are primarily interested in disorder-free systems that can be described by a periodic Hamiltonian. In that case, frustration is more precisely described as geometrical frustration, a concept that has received the following general definition: One speaks of geometrical frustra- tion when a local condition is unable to lead to a simple pattern for an extended system [1]. Typical examples are paving problems, where some figures such as triangles in two dimensions lead to regular, packed pavings while others such as pentagons are unable to lead to a compact, periodic structure.
    [Show full text]
  • Partially Frustrated Ising Models in Two Dimensions
    ✦ PHYSICAL REVIEW B 67, 224414 ⑦ 2003 Partially frustrated Ising models in two dimensions Jiansheng Wu and Daniel C. Mattis* Department of Physics, University of Utah, 115 S. 1400 East #201, Salt Lake City, Utah 84112-0830, USA ✦ ⑦ Received 3 March 2003; published 13 June 2003 We examine ordered, periodic, Ising models on a sq lattice at varying levels x of frustration. The thermo- ✺ dynamic singularity of the fully frustrated model (x ✺ 1) is at T 0 while those of partially frustrated lattices ❁ (0✱ x 1) occur at finite Tc . The critical indices in the partially frustrated lattices that we consider—including the logarithmic specific heat—are all identical to those in the ferromagnet (x ✺ 0.) We display exact values of Tc and of ground-state energy and entropy Eo and So ,atx ✺ 1, 2/3, 1/2 , 2/5 ,...,0. ✦ ✶ DOI: 10.1103/PhysRevB.67.224414 PACS number⑦ s : 75.10.Hk, 05.50. q ✁ INTRODUCTION just 2 sites 1 and 2 , it transforms into a regular array in ✁ which the antiferromagnetic AF bonds are all on the left This work discusses the phenomenon of partial vertical riser and all other bonds are ferromagnetic. Among ‘‘frustration.’’ 1 Interest in systems with ‘‘frozen-in’’ random- the many ground states8 of this configuration one finds two ✁ ness, commonly denoted ‘‘spin glasses,’’ has continued un- ferromagnetic states all spins up or all down and a ground- 2 ✄ ✉ ✉ abated since the 1970s. The only statistical systems with state energy E0 ✂ 4 J . Except in its response to an exter- any chance of being solved in closed form are Ising-model nal field, this model is an example of perfect geometrical spin glasses.
    [Show full text]
  • Advances in Artificial Spin Ice
    This is a repository copy of Advances in Artificial Spin Ice. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/153295/ Version: Accepted Version Article: Skjærvø, SH, Marrows, CH orcid.org/0000-0003-4812-6393, Stamps, RL et al. (1 more author) (2020) Advances in Artificial Spin Ice. Nature Reviews Physics, 2. pp. 13-28. ISSN 2522-5820 https://doi.org/10.1038/s42254-019-0118-3 This is protected by copyright. This is an author produced version of an article published in Nature Reviews Physics. Uploaded in accordance with the publisher's self-archiving policy. Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ 1 Contents 1. Introduction .................................................................................................................................... 2 2. Emergent Magnetic Monopoles ......................................................................................................
    [Show full text]
  • Magnetic Frustration and Multiferroics
    1 Magnetic frustration and multiferroics Virginie Simonet Institut Néel, CNRS/Université Grenoble Alpes, Grenoble, France HSC18, Grenoble, 2015 21/09/15 2 Outline of the lecture Reminder: Conventional Magnetism Magnetic frustration Introduction Competition of interactions Geometrical frustration Quantum case Role of the anisotropy Multiferroism Introduction About symmetries and chirality Examples Sorry, I will only speak about neutron scattering! HSC18, Grenoble, 2015 21/09/15 3 Reminder: conventional magnetism Temperature << interactions Temperature ≈ interactions Temperature >> interactions Ordered state Order onset Fluctuating disordered small fluctuations Heisenberg Hamiltonian = S~ J˜ S~ H − i ij j i,j J < 0 AFMX Order parameter Order parameter 2 T T=0 TN ≈ JS HSC18, Grenoble, 2015 21/09/15 4 Reminder: conventional magnetism Temperature << interactions Temperature >> interactions Ordered state Disordered state Magnetic frustration : generalities ⟨S (0)⋅S (r)⟩ magnons r 2 • Spin pair correlation function <Si(0)Sj(r) > <Si(0)Sj(r) >= S δij Magnetic frustration : generalities Real space ⟨S (0)⋅S (r)⟩ magnons order Reciprocal space S2 Reciprocal space Intensité w dispersion parameter S(Q) S(Q) BraggBragg peaks relation(s) Paramagnetic r diffuse scattering w(Q) -S2 order ∝ JS parameter Intensité w dispersion Bragg peaks relation(s)Q Q Q w(Q) HSC18, Grenoble, 2015 ∝ JS 21/09/15 magnetic order Q Q k b T 2 T =0 1 magnetic order J S k b T 2 T =0 1 J S 5 Reminder: conventional magnetism Temperature << interactions Temperature >> interactions
    [Show full text]
  • A New Geometrically Frustrated Cluster Spin-Glass
    LiZn2V3O8: A new geometrically frustrated cluster spin-glass S. Kundu,1, ∗ T. Dey,2 A. V. Mahajan,1 and N. B¨uttgen3 1Department of Physics, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India 2Experimental Physics VI, Center for Electronic Correlations and Magnetism, University of Augsburg, 86159 Augsburg, Germany 3Experimental Physics V, Center for Electronic Correlations and Magnetism, University of Augsburg, 86159 Augsburg, Germany (Dated: January 1, 2020) Abstract We have investigated the structural and magnetic properties of a new cubic spinel LiZn2V3O8 (LZVO) through x-ray diffraction, dc and ac susceptibility, magnetic relaxation, aging, memory effect, heat capacity and 7Li nuclear magnetic resonance (NMR) measurements. A Curie-Weiss fit of the dc susceptibility χdc(T ) yields a Curie-Weiss temperature θCW = -185 K. This suggests strong antiferromagnetic (AFM) interactions among the magnetic vanadium ions. The dc and ac susceptibility data indicate the spin-glass behavior below a freezing temperature Tf ' 3 K. The frequency dependence of the Tf is characterized by the Vogel-Fulcher law and critical dynamic scaling behavior or power law. 6 From both fitting, we obtained the value of the characteristic angular frequency !0 ≈ 3.56×10 Hz, the dynamic −6 exponent zv ≈ 2.65, and the critical time constant τ0 ≈ 1.82×10 s, which falls in the conventional range for typical cluster spin-glass (CSG) systems. The value of relative shift in freezing temperature δTf ' 0.039 supports a CSG ground states. We also found aging phenomena and memory effects in LZVO. The asymmetric response of the magnetic relaxation below Tf supports the hierarchical model.
    [Show full text]