DOCSLIB.ORG

A New Geometrically Frustrated Cluster Spin-Glass

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A New Geometrically Frustrated Cluster Spin-Glass LiZn2V3O8: A new geometrically frustrated cluster spin-glass S. Kundu,1, ∗ T. Dey,2 A. V. Mahajan,1 and N. B¨uttgen3 1Department of Physics, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India 2Experimental Physics VI, Center for Electronic Correlations and Magnetism, University of Augsburg, 86159 Augsburg, Germany 3Experimental Physics V, Center for Electronic Correlations and Magnetism, University of Augsburg, 86159 Augsburg, Germany (Dated: January 1, 2020) Abstract We have investigated the structural and magnetic properties of a new cubic spinel LiZn2V3O8 (LZVO) through x-ray diffraction, dc and ac susceptibility, magnetic relaxation, aging, memory effect, heat capacity and 7Li nuclear magnetic resonance (NMR) measurements. A Curie-Weiss fit of the dc susceptibility χdc(T ) yields a Curie-Weiss temperature θCW = -185 K. This suggests strong antiferromagnetic (AFM) interactions among the magnetic vanadium ions. The dc and ac susceptibility data indicate the spin-glass behavior below a freezing temperature Tf ' 3 K. The frequency dependence of the Tf is characterized by the Vogel-Fulcher law and critical dynamic scaling behavior or power law. 6 From both fitting, we obtained the value of the characteristic angular frequency !0 ≈ 3.56×10 Hz, the dynamic −6 exponent zv ≈ 2.65, and the critical time constant τ0 ≈ 1.82×10 s, which falls in the conventional range for typical cluster spin-glass (CSG) systems. The value of relative shift in freezing temperature δTf ' 0.039 supports a CSG ground states. We also found aging phenomena and memory effects in LZVO. The asymmetric response of the magnetic relaxation below Tf supports the hierarchical model. Heat capacity data show no long-range or short-range ordering down to 2 K. Only about 25% magnetic entropy change (∆Sm) signifies the presence of strong frustration in the system. The 7Li NMR spectra show a shift and broadening with decreasing temperature. The spin-lattice and spin-spin relaxation rates show anomalies due to spin freezing around 3 K as the bulk magnetization. PACS numbers: 75.50.Lk, 75.40.Cx, 76.60.-k I. INTRODUCTION tem. With a frustrated geometry, it exhibits a resonating valence-bond condensed state [14]. The strong interplay between the spin, charge, lattice and orbital degrees of Spinel oxides with the general formula AB2O4 have freedom in these transition metal oxides (TMO) are the provided an excellent arena for studying the effects of source of these novel magnetic properties. Motivated by geometrical frustration [1,2] and have seen a surge of these exotic behaviors of the cubic spinels, we decided to interest in the past decade due to a series of excit- investigate the mixed valent system LiZn2V3O8 (LZVO). ing experimental observations. In the cubic spinel, the Only the structural and electrical properties of LZVO B-sites form a corner shared, 3D tetrahedral network were reported long back in 1972 by B. Reuter and G. like the pyrochlore lattice which is geometrically frus- Colsmann [15]. The magnetic properties of LZVO have trated. Geometrical frustration arises when magnetic not been reported so far. As zinc prefers the A-site in moments occupying the B-sites interact antiferromagnet- spinel like in ZnCr2O4 [16, 17] and ZnV2O4 [18, 19], we ically with each other. With the intention of unraveling expect the site occupancy of LZVO to be represented as novel magnetic properties arising due to geometric frus- [Zn1:0(Li0:25V0:75)2O4]2 - where the octahedral B-site is tration, we were in the quest for new B-site cubic spinel occupied by Li and V in the 1:3 ratio. It will be inter- compounds. In this category, 3d-transition metal oxide 3+ 4+ esting to observe how the 25% dilution via non-magnetic LiV2O4 [3–5] (V :V = 1:1) is a well-studied system. lithium affects the magnetic properties of LZVO. Also, It shows heavy fermion behavior [6]. But with non- this system is amenable to nuclear magnetic resonance magnetic impurity (Zn/Ti) doping, it shows spin-glass (NMR) local probe measurement of 7Li nuclei. From behavior [7–9]. Recently studied mixed valent spinel 3+ stoichiometry, LZVO is a mixed valent spinel as in this system Zn3V3O8 or [Zn1:0(Zn0:25V0:75)2O4]2 with V : 11 4+ compound the average vanadium valence is + 3 : So it V = 2:1 [10] has been suggested to possess a cluster will be interesting to see whether this leads to tetrava- spin-glass ground state. Similarly, Li2ZnV3O8 (better lent and trivalent V in a 2:1 ratio. written as [Zn0:5Li0:5(Li0:25V0:75)2O4]2) containing only V4+ (S = 1=2) magnetic ions shows spin-glass behav- The motivation behind studying the system arXiv:1807.05612v3 [cond-mat.str-el] 31 Dec 2019 ior at low temperatures[11]. LiZn2Mo3O8 [12, 13] is an- LiZn2V3O8 is to contrast its properties with those other system stoichiometrically similar to our probed sys- of the resonating valence bond solid and cluster magnet compound LiZn2Mo3O8, whereas Zn3V3O8 (ZVO) was motivated by Majumdar-Ghosh chain system Ba3V3O8. Also, in LZVO, the effective spin value is close to S ∗Electronic address: [email protected] = 1/2 whereas in ZVO the effective spin is close to 1 ˚ S = 1. As quantum fluctuations are more prominent temperature (RT) with Cu Kα radiation (λ = 1:54182 A) in low spin systems, quantum effects in LZVO might on a PANalytical X’Pert PRO diffractometer. Magneti- play a dominant role compared to classical ZVO. Also, zation measurements were carried out in the temperature 3+ 4+ Zn3V3O8 (ZVO) has the ratio of V :V = 2:1 whereas range 1:8 − 400 K and the field range 0 − 70 kOe using for LZVO it is 1:2. In contrast, Li2ZnV3O8 contains a Quantum Design SQUID VSM. For the low-field mag- only S = 1=2 V4+. The strength of the exchange netization measurements, the reset magnet mode option couplings reflected in the Curie-Weiss temperature θCW of the SQUID VSM was used to set the field to zero. is about -370 K for ZVO while for Li2ZnV3O8 it is about Heat capacity measurements were performed in the tem- -210 K. For both ZVO and Li2ZnV3O8 the irreversible perature range 1:8 − 295 K and in the field range 0 − 90 temperature is Tirr ' 6.0 K and freezing temperatures kOe using the heat capacity option of a Quantum De- (Tf ) is around 3.75 K and 3.50 K respectively. sign PPMS. The NMR measurements were carried out In this work, we report sample preparation, structural using a phase-coherent pulse spectrometer on 7Li nuclei analysis, bulk magnetic properties, heat capacity and 7Li in a temperature range 1.8 - 200 K. We have measured NMR measurements on LZVO. The system crystallizes field sweep 7Li NMR spectra, spin-spin relaxation rate Fd¯3m 1 1 in the centrosymmetric space group with a site ( T2 ) and spin-lattice relaxation rate ( T1 ) at two different sharing between the lithium and the vanadium atoms at fixed radio frequencies (rf) of about 95 MHz and 30 MHz, the crystallographic 16c sites. Our magnetization data respectively. The spectra were measured using a con- π show no long-range ordering down to 2 K but we found ventional spin-echo sequence ( 2 − τecho − π). We have a splitting between the zero field cooled (ZFC) and field used the spin-echo pulse sequence with a variable delay cooled (FC) data at 3 K in low fields. A large Curie- time τD to measure T2 and a saturation pulse sequence θ = π Weiss temperature, CW - 185 K indicates strong an- ( 2 − τD − π) is used after a waiting time or last delay of tiferromagnetic (AFM) interactions between the mag- three to five times of T1 between each saturation pulse netic ions. Our frequency dependent ac susceptibility to measure T1. results indicate a spin-glass ground state. To know the spin-dynamics of the glassy phase in detail, we have car- ried out further magnetization measurements below the III. RESULTS AND DISCUSSION freezing temperature (Tf ) and observed clear signature of magnetic relaxation, aging effect and memory phe- nomena which are thought to be typical characteristics A. Crystal structure of spin-glasses. In memory effects, we observed that a To check for phase purity, we have measured the XRD small heating cycle erases its previous memory and reini- pattern of polycrystalline LZVO. The Rietveld refine- tializes the relaxation process. This type of asymmetric ment of LZVO (shown in Fig.1) revealed that it crys- response favors by the hierarchical model [20, 21]. The tallizes in the centrosymmetric cubic spinel Fd¯3m (227) inferred magnetic heat capacity has a broad maximum at space group. The two phase refinement of LZVO in- T ∼ 7 K but no sharp anomaly indicative of long-range dicates the presence of non-magnetic impurity phase ordering (LRO) is observed. The field swept 7Li NMR Li3VO4 (less than 2%) together with the main phase. spectra down to 1.8 K indicate the presence of an NMR The atomic positions obtained after Rietveld refinement line shift and gradual broadening of the spectra as T de- (using Fullprof suite [22]) are given in TableI. After re- creases. The spin-lattice and spin-spin relaxation rates finement, we obtained the lattice parameters as : a = b both show anomalies at a freezing temperature of 3 K. = c = 8.364 Å, α = β = γ = 900. The goodness of the Rietveld refinement is inferred from the following param- 2 eters χ : 1.37; Rp: 21.8%; Rwp: 10.7%; Rexp: 9.14%. II. EXPERIMENTAL DETAIL Note that from Rietveld refinement we can rewrite the chemical formula of LiZn2V3O8 as The polycrystalline LiZn2V3O8 sample was prepared [Zn1:0(Li0:241V0:759)2O4]2 like the cubic spinel gen- by conventional solid-state reaction techniques using high eral formula AB2O4.
Load more

Recommended publications
  • Introduction to Frustrated Magnetism
    Springer Series in Solid-State Sciences 164 Introduction to Frustrated Magnetism Materials, Experiments, Theory Bearbeitet von Claudine Lacroix, Philippe Mendels, Frédéric Mila 1. Auflage 2011. Buch. xxvi, 682 S. Hardcover ISBN 978 3 642 10588 3 Format (B x L): 15,5 x 23,5 cm Gewicht: 1339 g Weitere Fachgebiete > Physik, Astronomie > Elektrodynakmik, Optik > Magnetismus Zu Inhaltsverzeichnis schnell und portofrei erhältlich bei Die Online-Fachbuchhandlung beck-shop.de ist spezialisiert auf Fachbücher, insbesondere Recht, Steuern und Wirtschaft. Im Sortiment finden Sie alle Medien (Bücher, Zeitschriften, CDs, eBooks, etc.) aller Verlage. Ergänzt wird das Programm durch Services wie Neuerscheinungsdienst oder Zusammenstellungen von Büchern zu Sonderpreisen. Der Shop führt mehr als 8 Millionen Produkte. Chapter 1 Geometrically Frustrated Antiferromagnets: Statistical Mechanics and Dynamics John T. Chalker Abstract These lecture notes provide a simple overview of the physics of geomet- rically frustrated magnets. The emphasis is on classical and semiclassical treatments of the statistical mechanics and dynamics of frustrated Heisenberg models, and on the ways in which the results provide an understanding of some of the main observed properties of these systems. 1.1 Introduction This chapter is intended to give an introduction to the theory of thermal fluctua- tions and their consequences for static and dynamic correlations in geometrically frustrated antiferromagnets, focusing on the semiclassical limit, and to discuss how our theoretical understanding leads to an explanation of some of the main observed properties of these systems. A central theme will be the fact that simple, classi- cal models for highly frustrated magnets have a ground state degeneracy which is macroscopic, though accidental rather than a consequence of symmetries.
    [Show full text]
  • Geometrical Frustration, Phase Transitions and Dynamical Order
    Geometrical frustration, phase transitions and dynamical order The Tb2M2O7 compounds (M = Ti, Sn) Yann Chapuis PhD supervisor: Alain Yaouanc September 2009 Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 1 / 36 Outline 1 Introduction 2 The Tb2M2O7 compounds (M = Ti, Sn) 3 Tb2Ti2O7 : sample study 4 Crystal field levels 5 Conclusions Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 2 / 36 Outline 1 Introduction geometrical frustration connectivity and degeneracy spin ice 2 The Tb2M2O7 compounds (M = Ti, Sn) 3 Tb2Ti2O7 : sample study 4 Crystal field levels 5 Conclusions Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 3 / 36 Introduction geometrical frustration impossibility to satisfy simultaneously all the magnetic interactions frustration index : f = |θCW |/Tc ; frustration if f & 5 θCW : Curie-Weiss temperature Tc : transition temperature example of 2D Ising antiferromagnets Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 4 / 36 Introduction geometrical frustration triangular lattice Kagom´elattice garnet lattice pyrochlore lattice Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 5 / 36 Introduction connectivity and degeneracy low connectivity = large degeneracy Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 6 / 36 Introduction spin ice water ice (on the left) and spin ice (on the right) : analogy between protons displacement vectors and magnetic moments water ice = each oxygen with two protons close and two protons away (Pauling) spin ice = two spins in, two spins out → six equivalent configurations
    [Show full text]
  • Spin Glass Transitions in Geometrically Frustrated Magnets
    UNIVERSITY of CALIFORNIA SANTA CRUZ SPIN GLASS TRANSITIONS IN GEOMETRICALLY FRUSTRATED MAGNETS A thesis submitted in the partial satisfaction of the requirements for the degree of BACHELOR OF SCIENCE in APPLIED PHYSICS by CHRIS KINNEY 8 FEBRUARY 2016 The thesis of Chris Kinney is approved by Professor Arthur Ramirez Professor David Belanger Technical Advisor Thesis Advisor Professor Robert Johnson Chair, Department of Physics 0 Table of Contents Abstract……………………………………………………………………………...……………………………………………………………(2) Introduction………………………………………………………..…………………….……………………………………………………..(3) Data, Analysis and Methods……………………………………………………………………………………………………………..(6) Conclusion………………………………………………………………………………………………………………………………………(15) References………………………………………………………………………………………………………………………………………(16) 1 Abstract Spin glasses are magnetic systems exhibiting both quenched disorder and frustration, and have often been cited as examples of ‘complex systems.’ At the spin glass “freezing temperature” the spins stop fluctuating but do not exhibit long range orientational order. Geometrically frustrated magnets often exhibit spin glass behavior. In this paper spin glass physics is briefly discussed. We then discuss geometrically frustrated magnetism. This is followed by a discussion of experimental data taken in the lab on the magnetic freezing temperature of two different frustrated materials in various external magnetic fields. Two different known geometrically frustrated spin glass materials were cooled to helium temperatures. Magnetic moment data were collected
    [Show full text]
  • S41467-021-24636-1.Pdf
    ARTICLE https://doi.org/10.1038/s41467-021-24636-1 OPEN Dimensional reduction by geometrical frustration in a cubic antiferromagnet composed of tetrahedral clusters ✉ Ryutaro Okuma 1,2,7 , Maiko Kofu 3, Shinichiro Asai1, Maxim Avdeev 4,5, Akihiro Koda6, Hirotaka Okabe6, Masatoshi Hiraishi6, Soshi Takeshita 6, Kenji M. Kojima6,8, Ryosuke Kadono6, Takatsugu Masuda 1, Kenji Nakajima 3 & Zenji Hiroi 1 1234567890():,; Dimensionality is a critical factor in determining the properties of solids and is an apparent built- in character of the crystal structure. However, it can be an emergent and tunable property in geometrically frustrated spin systems. Here, we study the spin dynamics of the tetrahedral cluster antiferromagnet, pharmacosiderite, via muon spin resonance and neutron scattering. We find that the spin correlation exhibits a two-dimensional characteristic despite the isotropic connectivity of tetrahedral clusters made of spin 5/2 Fe3+ ions in the three-dimensional cubic crystal, which we ascribe to two-dimensionalisation by geometrical frustration based on spin wave calculations. Moreover, we suggest that even one-dimensionalisation occurs in the decoupled layers, generating low-energy and one-dimensional excitation modes, causing large spin fluctuation in the classical spin system. Pharmacosiderite facilitates studying the emergence of low-dimensionality and manipulating anisotropic responses arising from the dimensionality using an external magnetic field. 1 Institute for Solid State Physics, University of Tokyo, Kashiwa, Chiba, Japan. 2 Okinawa Institute of Science and Technology Graduate University, Onna, Okinawa, Japan. 3 Materials and Life Science Division, J-PARC Center, Japan Atomic Energy Agency, Tokai, Ibaraki, Japan. 4 Australian Nuclear Science and Technology Organisation, New Illawarra Road, Lucas Heights, Australia.
    [Show full text]
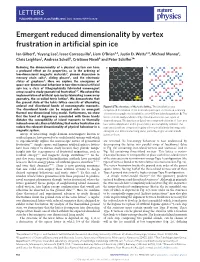
  • Emergent Reduced Dimensionality by Vertex Frustration in Artificial Spin
    LETTERS PUBLISHED ONLINE: 26 OCTOBER 2015 | DOI: 10.1038/NPHYS3520 Emergent reduced dimensionality by vertex frustration in artificial spin ice Ian Gilbert1, Yuyang Lao1, Isaac Carrasquillo1, Liam O’Brien2,3, Justin D. Watts2,4, Michael Manno2, Chris Leighton2, Andreas Scholl5, Cristiano Nisoli6 and Peter Schier1* Reducing the dimensionality of a physical system can have ab a profound eect on its properties, as in the ordering of low-dimensional magnetic materials1, phonon dispersion in mercury chain salts2, sliding phases3, and the electronic states of graphene4. Here we explore the emergence of quasi-one-dimensional behaviour in two-dimensional artificial spin ice, a class of lithographically fabricated nanomagnet arrays used to study geometrical frustration5–7. We extend the implementation of artificial spin ice by fabricating a new array 1 µm geometry, the so-called tetris lattice8. We demonstrate that the ground state of the tetris lattice consists of alternating ordered and disordered bands of nanomagnetic moments. Figure 1 | The structure of the tetris lattice. The tetris lattice is a The disordered bands can be mapped onto an emergent complicated decimation of the artificial square spin ice lattice. a, Scanning thermal one-dimensional Ising model. Furthermore, we show electron micrograph of a tetris lattice with 600 nm island separation. b, The that the level of degeneracy associated with these bands lattice is most easily understood by decomposition into two types of dictates the susceptibility of island moments to thermally diagonal stripes. The backbones (blue) are comprised of chains of four- and induced reversals, thus establishing that vertex frustration can two-vertex islands and, in the ground state, are completely ordered.
    [Show full text]
  • Resilience of the Topological Phases to Frustration Vanja Marić1,2, Fabio Franchini1, Domagoj Kuić1 & Salvatore Marco Giampaolo1*
    www.nature.com/scientificreports OPEN Resilience of the topological phases to frustration Vanja Marić1,2, Fabio Franchini1, Domagoj Kuić1 & Salvatore Marco Giampaolo1* Recently it was highlighted that one-dimensional antiferromagnetic spin models with frustrated boundary conditions, i.e. periodic boundary conditions in a ring with an odd number of elements, may show very peculiar behavior. Indeed the presence of frustrated boundary conditions can destroy the local magnetic orders presented by the models when diferent boundary conditions are taken into account and induce novel phase transitions. Motivated by these results, we analyze the efects of the introduction of frustrated boundary conditions on several models supporting (symmetry protected) topological orders, and compare our results with the ones obtained with diferent boundary conditions. None of the topological order phases analyzed are altered by this change. This observation leads naturally to the conjecture that topological phases of one-dimensional systems are in general not afected by topological frustration. Complex systems and their diferent ordered phases have always attracted a large interest, not only from a purely speculative point of view but also for the innumerable technological applications that exploit their characteristics1–3. In the middle of the last century, all the diferent phases of many-body systems obeying the laws of classical mechanics were classifed, using the Landau theory 4. According with this theory, diferent phases are characterized by diferent order parameters. Each one of them is uniquely associated to a particular kind of order that is related to the violation of a specifc symmetry (spontaneous symmetry breaking 5). It is therefore evident that, in the framework of Landau theory, the key role is played by the symmetries of the system, while other aspects, such as the boundary conditions, fall into the background and, generally, are considered not to be relevant for the presence or the absence of a particular kind of order.
    [Show full text]
  • Ordered Spin-Ice State in the Geometrically Frustrated Metallic-Ferromagnet Sm2mo2o7
    Ordered spin-ice state in the geometrically frustrated metallic-ferromagnet Sm2Mo2O7 Surjeet Singh1*, R. Suryanarayanan1, R. Tackett2, G. Lawes2, A. K. Sood3, P. Berthet1, 1 A. Revcolevschi 1Université Paris Sud, Laboratoire de Physico-Chimie de l'Etat Solide, UMR8182, Bât 414, Orsay, France. 2Department of Physics and Astronomy, Wayne State University, Detroit, MI 48202 USA. 3Department of Physics, Indian Institute of Science, Bangalore 560012, India. The recent discovery of Spin-ice is a spectacular example of non-coplanar spin arrangements that can arise in the pyrochlore A2B2O7 structure. We present magnetic and thermodynamic studies on the metallic-ferromagnet pyrochlore Sm2Mo2O7. Our studies, carried out on oriented crystals, suggest that the Sm spins have an ordered spin-ice ground state below about T* = 15 K. The temperature- and field-evolution of the ordered spin-ice state are governed by an antiferromagnetic coupling between the Sm and Mo spins. We propose that as a consequence of a robust feature of this coupling, the tetrahedra aligned with the external field adopt a “1-in, 3-out” spin structure as opposed to “3-in, 1-out” in dipolar spin ices, as the field exceeds a critical value. PACS: 75.30 –m, 75.30.Kz, 75.40Cx, 81.30-h Geometrical frustration arises when the magnetic interactions on a lattice are incompatible with the underlying crystalline symmetry. Systems with magnetic ions on triangular or tetrahedral lattices can exhibit geometrical frustration, which is often relieved at sufficiently low temperatures by weak residual interactions giving way to complex magnetic ground states1. One particularly important example of geometrical frustration arises in materials based on the pyrochlore structure (A2B2O7), where A and B ions form networks of corner-linked tetrahedra displaced by half the unit cell dimensions from each other.
    [Show full text]
  • Frustrated Spin Systems
    7 Frustrated Spin Systems Fred´ eric´ Mila Institute of Theoretical Physics Ecole Polytechnique Fed´ erale´ de Lausanne 1015 Lausanne, Switzerland Contents 1 Introduction 2 2 Competing interactions and degeneracy 3 2.1 Ising . 3 2.2 Heisenberg . 6 3 Classical ground-state correlations 8 3.1 Algebraic correlations . 8 3.2 Dipolar correlations . 10 4 Order by disorder 12 4.1 Quantum fluctuations . 12 4.2 Thermal fluctuations . 14 5 Alternatives to magnetic long-range order in Heisenberg models 14 5.1 Spin gap . 15 5.2 Resonating Valence Bond spin liquids . 17 5.3 Algebraic spin liquids . 21 5.4 Chiral spin liquids . 23 5.5 Nematic order . 24 6 Conclusion 27 E. Pavarini, E. Koch, and P. Coleman (eds.) Many-Body Physics: From Kondo to Hubbard Modeling and Simulation Vol. 5 Forschungszentrum Julich,¨ 2015, ISBN 978-3-95806-074-6 http://www.cond-mat.de/events/correl15 7.2 Fred´ eric´ Mila 1 Introduction In the field of magnetism, the word frustration was first introduced in the context of spin glasses to describe the impossibility of simultaneously satisfying all exchange processes. In this lec- ture, we are primarily interested in disorder-free systems that can be described by a periodic Hamiltonian. In that case, frustration is more precisely described as geometrical frustration, a concept that has received the following general definition: One speaks of geometrical frustra- tion when a local condition is unable to lead to a simple pattern for an extended system [1]. Typical examples are paving problems, where some figures such as triangles in two dimensions lead to regular, packed pavings while others such as pentagons are unable to lead to a compact, periodic structure.
    [Show full text]
  • Partially Frustrated Ising Models in Two Dimensions
    ✦ PHYSICAL REVIEW B 67, 224414 ⑦ 2003 Partially frustrated Ising models in two dimensions Jiansheng Wu and Daniel C. Mattis* Department of Physics, University of Utah, 115 S. 1400 East #201, Salt Lake City, Utah 84112-0830, USA ✦ ⑦ Received 3 March 2003; published 13 June 2003 We examine ordered, periodic, Ising models on a sq lattice at varying levels x of frustration. The thermo- ✺ dynamic singularity of the fully frustrated model (x ✺ 1) is at T 0 while those of partially frustrated lattices ❁ (0✱ x 1) occur at finite Tc . The critical indices in the partially frustrated lattices that we consider—including the logarithmic specific heat—are all identical to those in the ferromagnet (x ✺ 0.) We display exact values of Tc and of ground-state energy and entropy Eo and So ,atx ✺ 1, 2/3, 1/2 , 2/5 ,...,0. ✦ ✶ DOI: 10.1103/PhysRevB.67.224414 PACS number⑦ s : 75.10.Hk, 05.50. q ✁ INTRODUCTION just 2 sites 1 and 2 , it transforms into a regular array in ✁ which the antiferromagnetic AF bonds are all on the left This work discusses the phenomenon of partial vertical riser and all other bonds are ferromagnetic. Among ‘‘frustration.’’ 1 Interest in systems with ‘‘frozen-in’’ random- the many ground states8 of this configuration one finds two ✁ ness, commonly denoted ‘‘spin glasses,’’ has continued un- ferromagnetic states all spins up or all down and a ground- 2 ✄ ✉ ✉ abated since the 1970s. The only statistical systems with state energy E0 ✂ 4 J . Except in its response to an exter- any chance of being solved in closed form are Ising-model nal field, this model is an example of perfect geometrical spin glasses.
    [Show full text]
  • Advances in Artificial Spin Ice
    This is a repository copy of Advances in Artificial Spin Ice. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/153295/ Version: Accepted Version Article: Skjærvø, SH, Marrows, CH orcid.org/0000-0003-4812-6393, Stamps, RL et al. (1 more author) (2020) Advances in Artificial Spin Ice. Nature Reviews Physics, 2. pp. 13-28. ISSN 2522-5820 https://doi.org/10.1038/s42254-019-0118-3 This is protected by copyright. This is an author produced version of an article published in Nature Reviews Physics. Uploaded in accordance with the publisher's self-archiving policy. Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ 1 Contents 1. Introduction .................................................................................................................................... 2 2. Emergent Magnetic Monopoles ......................................................................................................
    [Show full text]
  • Magnetic Frustration and Multiferroics
    1 Magnetic frustration and multiferroics Virginie Simonet Institut Néel, CNRS/Université Grenoble Alpes, Grenoble, France HSC18, Grenoble, 2015 21/09/15 2 Outline of the lecture Reminder: Conventional Magnetism Magnetic frustration Introduction Competition of interactions Geometrical frustration Quantum case Role of the anisotropy Multiferroism Introduction About symmetries and chirality Examples Sorry, I will only speak about neutron scattering! HSC18, Grenoble, 2015 21/09/15 3 Reminder: conventional magnetism Temperature << interactions Temperature ≈ interactions Temperature >> interactions Ordered state Order onset Fluctuating disordered small fluctuations Heisenberg Hamiltonian = S~ J˜ S~ H − i ij j i,j J < 0 AFMX Order parameter Order parameter 2 T T=0 TN ≈ JS HSC18, Grenoble, 2015 21/09/15 4 Reminder: conventional magnetism Temperature << interactions Temperature >> interactions Ordered state Disordered state Magnetic frustration : generalities ⟨S (0)⋅S (r)⟩ magnons r 2 • Spin pair correlation function <Si(0)Sj(r) > <Si(0)Sj(r) >= S δij Magnetic frustration : generalities Real space ⟨S (0)⋅S (r)⟩ magnons order Reciprocal space S2 Reciprocal space Intensité w dispersion parameter S(Q) S(Q) BraggBragg peaks relation(s) Paramagnetic r diffuse scattering w(Q) -S2 order ∝ JS parameter Intensité w dispersion Bragg peaks relation(s)Q Q Q w(Q) HSC18, Grenoble, 2015 ∝ JS 21/09/15 magnetic order Q Q k b T 2 T =0 1 magnetic order J S k b T 2 T =0 1 J S 5 Reminder: conventional magnetism Temperature << interactions Temperature >> interactions
    [Show full text]
  • Quantum Spin-Liquid States in an Organic Magnetic Layer And
    Quantum spin-liquid states in an organic magnetic layer and molecular rotor hybrid Peter´ Szirmaia ,Cecile´ Mezi´ ere` b, Guillaume Bastienc , Pawel Wzietekd , Patrick Batailb , Edoardo Martinoa, Konstantins Mantulnikovsa, Andrea Pisonia, Kira Riedle , Stephen Cottrellf, Christopher Bainesg ,Laszl´ o´ Forro´ a,1, and Balint´ Nafr´ adi´ a,1 aLaboratory of Physics of Complex Matter, Ecole Polytechnique Fed´ erale´ de Lausanne, CH-1015 Lausanne, Switzerland, 1015; bLaboratoire MOLTECH-Anjou, CNRS and Universite´ d’Angers, 49045 Angers, France, 49045 Angers; cInstitute of Organic Chemistry and Biochemistry, Academy of Science of the Czech Republic, 166 10 Prague 6, Czech Republic; dLaboratoire de Physique des Solides, CNRS and Universite´ de Paris-Sud, 91405 Orsay, France, 91405; eInstitut fur Theoretische Physik, Goethe-Universitat Frankfurt, 60438 Frankfurt am Main, Germany; fISIS Muon Group, Science and Technology Facilities Council (STFC), Didcot OX11 0QX, United Kingdom; and gLaboratory for Muon Spin Spectroscopy, Paul Scherrer Institute, 5232 Villigen, Switzerland Edited by Stuart Brown, University of California, Los Angeles, CA, and accepted by Editorial Board Member Zachary Fisk September 30, 2020 (received for review January 6, 2020) The exotic properties of quantum spin liquids (QSLs) have continu- tion and quenched bond randomness to induce or support a QSL ally been of interest since Anderson’s 1973 ground-breaking idea. state (23–25). It came as a surprise that the X-ray irradiation Geometrical frustration, quantum fluctuations, and low dimen- of the weakly frustrated, long-range ordered antiferromagnet, sionality are the most often evoked material’s characteristics κ-(ET)2Cu[N(CN)2]Cl was reported to lead to the stabilization that favor the long-range fluctuating spin state without freez- of a disorder-driven QSL state (26).
    [Show full text]