'Spin Ice' in a Geometrically Frustrated Lattice of Nanoscale Ferromagnetic
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Investigation of the Magnetic and Magnetocaloric Properties of Complex Lanthanide Oxides
Investigation of the magnetic and magnetocaloric properties of complex lanthanide oxides Paromita Mukherjee Department of Physics University of Cambridge This dissertation is submitted for the degree of Doctor of Philosophy King’s College April 2018 This thesis is dedicated to my parents. Declaration I hereby declare that except where specific reference is made to the work of others, the contents of this dissertation are original and have not been submitted in whole or in part for consideration for any other degree or qualification in the University of Cambridge, or any other university. This dissertation is my own work and contains nothing which is the outcome of work done in collaboration, except as specified in the text and Acknowledgements. This dissertation contains fewer than 60,000 words including abstract, tables, footnotes and appendices. Some of the work described herein has been published as follows: Chapter 3 is an expanded version of: P. Mukherjee, A. C. Sackville Hamilton, H. F. J. Glass, S. E. Dutton, Sensitivity of magnetic properties to chemical pressure in lanthanide garnets Ln3A2X3O12, Ln = Gd, Tb, Dy, Ho, A = Ga, Sc, In, Te, X = Ga, Al, Li, Journal of Physics: Condensed Matter 29, 405808 (2017). Chapter 4 contains material from: P. Mukherjee, S. E. Dutton, Enhanced magnetocaloric effect from Cr substitution in Ising lanthanide gallium garnets Ln3CrGa4O12 (Ln = Tb, Dy, Ho), Advanced Functional Materials 27, 1701950 (2017). P. Mukherjee, H. F. J. Glass, E. Suard, and S. E. Dutton, Relieving the frustration through Mn3+ substitution in holmium gallium garnet, Physical Review B 96, 140412(R) (2017). Chapter 5 contains material from: P. -

A Highly Scalable Dynamical Matrix Approach Applied to a Fibonacci- Distorted Artificial Spin Ice
University of Kentucky UKnowledge Physics and Astronomy Faculty Publications Physics and Astronomy 3-8-2021 Magnetic Normal Mode Calculations in Big Systems: A Highly Scalable Dynamical Matrix Approach Applied to a Fibonacci- Distorted Artificial Spin Ice Loris Giovannini Università di Ferrara, Italy Barry W. Farmer University of Kentucky, [email protected] Justin S. Woods University of Kentucky, [email protected] Ali Frotanpour University of Kentucky, [email protected] Lance E. De Long University of Kentucky, [email protected] Follow this and additional works at: https://uknowledge.uky.edu/physastron_facpub See next page for additional authors Part of the Physics Commons Right click to open a feedback form in a new tab to let us know how this document benefits ou.y Repository Citation Giovannini, Loris; Farmer, Barry W.; Woods, Justin S.; Frotanpour, Ali; De Long, Lance E.; and Montoncello, Federico, "Magnetic Normal Mode Calculations in Big Systems: A Highly Scalable Dynamical Matrix Approach Applied to a Fibonacci-Distorted Artificial Spin Ice" (2021). Physics and Astronomy Faculty Publications. 673. https://uknowledge.uky.edu/physastron_facpub/673 This Article is brought to you for free and open access by the Physics and Astronomy at UKnowledge. It has been accepted for inclusion in Physics and Astronomy Faculty Publications by an authorized administrator of UKnowledge. For more information, please contact [email protected]. Magnetic Normal Mode Calculations in Big Systems: A Highly Scalable Dynamical Matrix Approach Applied to a Fibonacci-Distorted Artificial Spin Ice Digital Object Identifier (DOI) https://doi.org/10.3390/magnetochemistry7030034 Notes/Citation Information Published in Magnetochemistry, v. -

Emergence of Nontrivial Spin Textures in Frustrated Van Der Waals Ferromagnets
nanomaterials Article Emergence of Nontrivial Spin Textures in Frustrated Van Der Waals Ferromagnets Aniekan Magnus Ukpong Theoretical and Computational Condensed Matter and Materials Physics Group, School of Chemistry and Physics, University of KwaZulu-Natal, Pietermaritzburg 3201, South Africa; [email protected]; Tel.: +27-33-260-5875 Abstract: In this work, first principles ground state calculations are combined with the dynamic evolution of a classical spin Hamiltonian to study the metamagnetic transitions associated with the field dependence of magnetic properties in frustrated van der Waals ferromagnets. Dynamically stabilized spin textures are obtained relative to the direction of spin quantization as stochastic solutions of the Landau–Lifshitz–Gilbert–Slonczewski equation under the flow of the spin current. By explicitly considering the spin signatures that arise from geometrical frustrations at interfaces, we may observe the emergence of a magnetic skyrmion spin texture and characterize the formation under competing internal fields. The analysis of coercivity and magnetic hysteresis reveals a dynamic switch from a soft to hard magnetic configuration when considering the spin Hall effect on the skyrmion. It is found that heavy metals in capped multilayer heterostructure stacks host field-tunable spiral skyrmions that could serve as unique channels for carrier transport. The results are discussed to show the possibility of using dynamically switchable magnetic bits to read and write data without the need for a spin transfer torque. These results offer insight to the spin transport signatures that Citation: Ukpong, A.M. Emergence dynamically arise from metamagnetic transitions in spintronic devices. of Nontrivial Spin Textures in Frustrated Van Der Waals Keywords: spin current; van der Waals ferromagnets; magnetic skyrmion; spin Hall effect Ferromagnets. -

Quantum Spin-Ice and Dimer Models with Rydberg Atoms
PHYSICAL REVIEW X 4, 041037 (2014) Quantum Spin-Ice and Dimer Models with Rydberg Atoms A. W. Glaetzle,1,2,* M. Dalmonte,1,2 R. Nath,1,2,3 I. Rousochatzakis,4 R. Moessner,4 and P. Zoller1,2 1Institute for Quantum Optics and Quantum Information of the Austrian Academy of Sciences, A-6020 Innsbruck, Austria 2Institute for Theoretical Physics, University of Innsbruck, A-6020 Innsbruck, Austria 3Indian Institute of Science Education and Research, Pune 411 008, India 4Max Planck Institute for the Physics of Complex Systems, D-01187 Dresden, Germany (Received 21 April 2014; revised manuscript received 27 August 2014; published 25 November 2014) Quantum spin-ice represents a paradigmatic example of how the physics of frustrated magnets is related to gauge theories. In the present work, we address the problem of approximately realizing quantum spin ice in two dimensions with cold atoms in optical lattices. The relevant interactions are obtained by weakly laser-admixing Rydberg states to the atomic ground-states, exploiting the strong angular dependence of van der Waals interactions between Rydberg p states together with the possibility of designing steplike potentials. This allows us to implement Abelian gauge theories in a series of geometries, which could be demonstrated within state-of-the-art atomic Rydberg experiments. We numerically analyze the family of resulting microscopic Hamiltonians and find that they exhibit both classical and quantum order by disorder, the latter yielding a quantum plaquette valence bond solid. We also present strategies to implement Abelian gauge theories using both s- and p-Rydberg states in exotic geometries, e.g., on a 4–8 lattice. -

Introduction to Frustrated Magnetism
Springer Series in Solid-State Sciences 164 Introduction to Frustrated Magnetism Materials, Experiments, Theory Bearbeitet von Claudine Lacroix, Philippe Mendels, Frédéric Mila 1. Auflage 2011. Buch. xxvi, 682 S. Hardcover ISBN 978 3 642 10588 3 Format (B x L): 15,5 x 23,5 cm Gewicht: 1339 g Weitere Fachgebiete > Physik, Astronomie > Elektrodynakmik, Optik > Magnetismus Zu Inhaltsverzeichnis schnell und portofrei erhältlich bei Die Online-Fachbuchhandlung beck-shop.de ist spezialisiert auf Fachbücher, insbesondere Recht, Steuern und Wirtschaft. Im Sortiment finden Sie alle Medien (Bücher, Zeitschriften, CDs, eBooks, etc.) aller Verlage. Ergänzt wird das Programm durch Services wie Neuerscheinungsdienst oder Zusammenstellungen von Büchern zu Sonderpreisen. Der Shop führt mehr als 8 Millionen Produkte. Chapter 1 Geometrically Frustrated Antiferromagnets: Statistical Mechanics and Dynamics John T. Chalker Abstract These lecture notes provide a simple overview of the physics of geomet- rically frustrated magnets. The emphasis is on classical and semiclassical treatments of the statistical mechanics and dynamics of frustrated Heisenberg models, and on the ways in which the results provide an understanding of some of the main observed properties of these systems. 1.1 Introduction This chapter is intended to give an introduction to the theory of thermal fluctua- tions and their consequences for static and dynamic correlations in geometrically frustrated antiferromagnets, focusing on the semiclassical limit, and to discuss how our theoretical understanding leads to an explanation of some of the main observed properties of these systems. A central theme will be the fact that simple, classi- cal models for highly frustrated magnets have a ground state degeneracy which is macroscopic, though accidental rather than a consequence of symmetries. -

Geometrical Frustration, Phase Transitions and Dynamical Order
Geometrical frustration, phase transitions and dynamical order The Tb2M2O7 compounds (M = Ti, Sn) Yann Chapuis PhD supervisor: Alain Yaouanc September 2009 Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 1 / 36 Outline 1 Introduction 2 The Tb2M2O7 compounds (M = Ti, Sn) 3 Tb2Ti2O7 : sample study 4 Crystal field levels 5 Conclusions Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 2 / 36 Outline 1 Introduction geometrical frustration connectivity and degeneracy spin ice 2 The Tb2M2O7 compounds (M = Ti, Sn) 3 Tb2Ti2O7 : sample study 4 Crystal field levels 5 Conclusions Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 3 / 36 Introduction geometrical frustration impossibility to satisfy simultaneously all the magnetic interactions frustration index : f = |θCW |/Tc ; frustration if f & 5 θCW : Curie-Weiss temperature Tc : transition temperature example of 2D Ising antiferromagnets Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 4 / 36 Introduction geometrical frustration triangular lattice Kagom´elattice garnet lattice pyrochlore lattice Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 5 / 36 Introduction connectivity and degeneracy low connectivity = large degeneracy Yann Chapuis (CEA/Grenoble - Inac/SPSMS) September 2009 6 / 36 Introduction spin ice water ice (on the left) and spin ice (on the right) : analogy between protons displacement vectors and magnetic moments water ice = each oxygen with two protons close and two protons away (Pauling) spin ice = two spins in, two spins out → six equivalent configurations -

Spin Glass Transitions in Geometrically Frustrated Magnets
UNIVERSITY of CALIFORNIA SANTA CRUZ SPIN GLASS TRANSITIONS IN GEOMETRICALLY FRUSTRATED MAGNETS A thesis submitted in the partial satisfaction of the requirements for the degree of BACHELOR OF SCIENCE in APPLIED PHYSICS by CHRIS KINNEY 8 FEBRUARY 2016 The thesis of Chris Kinney is approved by Professor Arthur Ramirez Professor David Belanger Technical Advisor Thesis Advisor Professor Robert Johnson Chair, Department of Physics 0 Table of Contents Abstract……………………………………………………………………………...……………………………………………………………(2) Introduction………………………………………………………..…………………….……………………………………………………..(3) Data, Analysis and Methods……………………………………………………………………………………………………………..(6) Conclusion………………………………………………………………………………………………………………………………………(15) References………………………………………………………………………………………………………………………………………(16) 1 Abstract Spin glasses are magnetic systems exhibiting both quenched disorder and frustration, and have often been cited as examples of ‘complex systems.’ At the spin glass “freezing temperature” the spins stop fluctuating but do not exhibit long range orientational order. Geometrically frustrated magnets often exhibit spin glass behavior. In this paper spin glass physics is briefly discussed. We then discuss geometrically frustrated magnetism. This is followed by a discussion of experimental data taken in the lab on the magnetic freezing temperature of two different frustrated materials in various external magnetic fields. Two different known geometrically frustrated spin glass materials were cooled to helium temperatures. Magnetic moment data were collected -

Spectroscopy of Spinons in Coulomb Quantum Spin Liquids
MIT-CTP-5122 Spectroscopy of spinons in Coulomb quantum spin liquids Siddhardh C. Morampudi,1 Frank Wilczek,2, 3, 4, 5, 6 and Chris R. Laumann1 1Department of Physics, Boston University, Boston, MA 02215, USA 2Center for Theoretical Physics, MIT, Cambridge MA 02139, USA 3T. D. Lee Institute, Shanghai, China 4Wilczek Quantum Center, Department of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China 5Department of Physics, Stockholm University, Stockholm Sweden 6Department of Physics and Origins Project, Arizona State University, Tempe AZ 25287 USA We calculate the effect of the emergent photon on threshold production of spinons in U(1) Coulomb spin liquids such as quantum spin ice. The emergent Coulomb interaction modifies the threshold production cross- section dramatically, changing the weak turn-on expected from the density of states to an abrupt onset reflecting the basic coupling parameters. The slow photon typical in existing lattice models and materials suppresses the intensity at finite momentum and allows profuse Cerenkov radiation beyond a critical momentum. These features are broadly consistent with recent numerical and experimental results. Quantum spin liquids are low temperature phases of mag- The most dramatic consequence of the Coulomb interaction netic materials in which quantum fluctuations prevent the between the spinons is a universal non-perturbative enhance- establishment of long-range magnetic order. Theoretically, ment of the threshold cross section for spinon pair production these phases support exotic fractionalized spin excitations at small momentum q. In this regime, the dynamic structure (spinons) and emergent gauge fields [1–4]. One of the most factor in the spin-flip sector observed in neutron scattering ex- promising candidate class of these phases are U(1) Coulomb hibits a step discontinuity, quantum spin liquids such as quantum spin ice - these are ex- 1 q 2 q2 pected to realize an emergent quantum electrodynamics [5– S(q;!) ∼ S0 1 − θ(! − 2∆ − ) (1) 11]. -

S41467-021-24636-1.Pdf
ARTICLE https://doi.org/10.1038/s41467-021-24636-1 OPEN Dimensional reduction by geometrical frustration in a cubic antiferromagnet composed of tetrahedral clusters ✉ Ryutaro Okuma 1,2,7 , Maiko Kofu 3, Shinichiro Asai1, Maxim Avdeev 4,5, Akihiro Koda6, Hirotaka Okabe6, Masatoshi Hiraishi6, Soshi Takeshita 6, Kenji M. Kojima6,8, Ryosuke Kadono6, Takatsugu Masuda 1, Kenji Nakajima 3 & Zenji Hiroi 1 1234567890():,; Dimensionality is a critical factor in determining the properties of solids and is an apparent built- in character of the crystal structure. However, it can be an emergent and tunable property in geometrically frustrated spin systems. Here, we study the spin dynamics of the tetrahedral cluster antiferromagnet, pharmacosiderite, via muon spin resonance and neutron scattering. We find that the spin correlation exhibits a two-dimensional characteristic despite the isotropic connectivity of tetrahedral clusters made of spin 5/2 Fe3+ ions in the three-dimensional cubic crystal, which we ascribe to two-dimensionalisation by geometrical frustration based on spin wave calculations. Moreover, we suggest that even one-dimensionalisation occurs in the decoupled layers, generating low-energy and one-dimensional excitation modes, causing large spin fluctuation in the classical spin system. Pharmacosiderite facilitates studying the emergence of low-dimensionality and manipulating anisotropic responses arising from the dimensionality using an external magnetic field. 1 Institute for Solid State Physics, University of Tokyo, Kashiwa, Chiba, Japan. 2 Okinawa Institute of Science and Technology Graduate University, Onna, Okinawa, Japan. 3 Materials and Life Science Division, J-PARC Center, Japan Atomic Energy Agency, Tokai, Ibaraki, Japan. 4 Australian Nuclear Science and Technology Organisation, New Illawarra Road, Lucas Heights, Australia. -
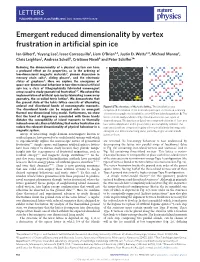
Emergent Reduced Dimensionality by Vertex Frustration in Artificial Spin
LETTERS PUBLISHED ONLINE: 26 OCTOBER 2015 | DOI: 10.1038/NPHYS3520 Emergent reduced dimensionality by vertex frustration in artificial spin ice Ian Gilbert1, Yuyang Lao1, Isaac Carrasquillo1, Liam O’Brien2,3, Justin D. Watts2,4, Michael Manno2, Chris Leighton2, Andreas Scholl5, Cristiano Nisoli6 and Peter Schier1* Reducing the dimensionality of a physical system can have ab a profound eect on its properties, as in the ordering of low-dimensional magnetic materials1, phonon dispersion in mercury chain salts2, sliding phases3, and the electronic states of graphene4. Here we explore the emergence of quasi-one-dimensional behaviour in two-dimensional artificial spin ice, a class of lithographically fabricated nanomagnet arrays used to study geometrical frustration5–7. We extend the implementation of artificial spin ice by fabricating a new array 1 µm geometry, the so-called tetris lattice8. We demonstrate that the ground state of the tetris lattice consists of alternating ordered and disordered bands of nanomagnetic moments. Figure 1 | The structure of the tetris lattice. The tetris lattice is a The disordered bands can be mapped onto an emergent complicated decimation of the artificial square spin ice lattice. a, Scanning thermal one-dimensional Ising model. Furthermore, we show electron micrograph of a tetris lattice with 600 nm island separation. b, The that the level of degeneracy associated with these bands lattice is most easily understood by decomposition into two types of dictates the susceptibility of island moments to thermally diagonal stripes. The backbones (blue) are comprised of chains of four- and induced reversals, thus establishing that vertex frustration can two-vertex islands and, in the ground state, are completely ordered. -

Magnetic Monopoles in Spin Ice
Master of Science Thesis Magnetic Monopoles in Spin Ice Axel Nordstr¨om Supervisor: Patrik Henelius Department of Theoretical Physics, School of Engineering Sciences Royal Institute of Technology, SE-106 91 Stockholm, Sweden Stockholm, Sweden 2014 Typeset in LATEX Examensarbete inom ¨amnet teoretisk fysik f¨or avl¨aggande av civilingenj¨orsexamen inom utbildningstprogrammet Teknisk fysik. Graduation thesis on the subject Theoretical Physics for the degree of Master of Science in Engineering from the School of Engineering Sciences. TRITA-FYS 2014:26 ISSN 0280-316X ISRN KTH/FYS/{14:26{SE © Axel Nordstr¨om,May 2014 Printed in Sweden by Universitetsservice US AB, Stockholm May 2014 Abstract In this thesis, we investigate the behaviour of magnetic monopoles in spin ice when an external magnetic field is applied. We find that steady state direct currents of magnetic monopoles cannot be maintained for long and consider the possibility of alternating magnetic currents by investigating the alternating current susceptibility using both analytical and Monte Carlo techniques. Moreover, we look at the transition that occurs when a magnetic field is ap- plied in a 111 direction. We show that the transition is a continuous crossover rather thanh a phasei transition in the nearest neighbour model and we study the behaviour of the system during the crossover, especially at the critical field where a temperature independent state appears. Using Monte Carlo methods and analyti- cal methods based on the Bethe approximation, we find that the mean monopole density is 0.4 monopoles per tetrahedron in the temperature independent state at the critical field. Keywords: spin ice, magnetic monopoles, phase transitions. -

Emergent Phenomena in Spin Crossover Systems
Emergent Phenomena in Spin Crossover Systems Jace Alex Cruddas B.Sc. (Hons) Candidate’s ORCID A thesis submitted for the degree of Doctor of Philosophy at The University of Queensland in Year School of Mathematics and Physics Abstract In general, a spin crossover (SCO) system is any complex, material or framework containing two thermodynamically accessible spin-states: one high-spin (HS) and one low-spin (LS). The transition between spin-states is addressable by temperature, pressure, light irradiation, electric and magnetic fields, and chemical environment. The transition itself can be first-order, exhibiting hysteresis, continuous or a crossover. Typically, accompanied by the ferroelastic ordering of spin-states. It can also be part of an incomplete or multi-step transition accompanied by the antiferroelastic ordering of spin-states. In general, any alterations to the structural characteristics of SCO systems can have an effect on their bulk properties and behaviours. Consequently, constructing structure-property relations has traditionally been an extremely challenging task, and one of both great theoretical and experimental interest. Understanding the mechanisms behind these bulk properties and behaviours could lead to the rational design of SCO systems with enhanced applications and the synthesis of novel properties and behaviours. In this thesis we show that a simple, elastic model of SCO systems hosts almost all experimentally reported SCO properties and behaviours. We demonstrate clear structure-property relations that explain these results, derive the mechanisms of multi-step transitions and explain why and how intermolecular interactions play a role. We also propose that a new exotic state of matter could exist in elastically frustrated SCO materials and frameworks.