Digital Data Processing Strategies for Large Area Maskless Photopolymerization Anirudh Rudraraju, Suman Das , Georgia Institute of Technology
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Openscad User Manual (PDF)
OpenSCAD User Manual Contents 1 Introduction 1.1 Additional Resources 1.2 History 2 The OpenSCAD User Manual 3 The OpenSCAD Language Reference 4 Work in progress 5 Contents 6 Chapter 1 -- First Steps 6.1 Compiling and rendering our first model 6.2 See also 6.3 See also 6.3.1 There is no semicolon following the translate command 6.3.2 See Also 6.3.3 See Also 6.4 CGAL surfaces 6.5 CGAL grid only 6.6 The OpenCSG view 6.7 The Thrown Together View 6.8 See also 6.9 References 7 Chapter 2 -- The OpenSCAD User Interface 7.1 User Interface 7.1.1 Viewing area 7.1.2 Console window 7.1.3 Text editor 7.2 Interactive modification of the numerical value 7.3 View navigation 7.4 View setup 7.4.1 Render modes 7.4.1.1 OpenCSG (F9) 7.4.1.1.1 Implementation Details 7.4.1.2 CGAL (Surfaces and Grid, F10 and F11) 7.4.1.2.1 Implementation Details 7.4.2 View options 7.4.2.1 Show Edges (Ctrl+1) 7.4.2.2 Show Axes (Ctrl+2) 7.4.2.3 Show Crosshairs (Ctrl+3) 7.4.3 Animation 7.4.4 View alignment 7.5 Dodecahedron 7.6 Icosahedron 7.7 Half-pyramid 7.8 Bounding Box 7.9 Linear Extrude extended use examples 7.9.1 Linear Extrude with Scale as an interpolated function 7.9.2 Linear Extrude with Twist as an interpolated function 7.9.3 Linear Extrude with Twist and Scale as interpolated functions 7.10 Rocket 7.11 Horns 7.12 Strandbeest 7.13 Previous 7.14 Next 7.14.1 Command line usage 7.14.2 Export options 7.14.2.1 Camera and image output 7.14.3 Constants 7.14.4 Command to build required files 7.14.5 Processing all .scad files in a folder 7.14.6 Makefile example 7.14.6.1 Automatic -

HOW to PREPARE AEC FILES for 3D PRINTING and Start Producing Physical 3D Models in Hours Instead of Weeks > > HOW to PREPARE AEC FILES for 3D PRINTING 2
HOW TO PREPARE AEC FILES FOR 3D PRINTING And Start Producing Physical 3D Models in Hours Instead of Weeks > > HOW TO PREPARE AEC FILES FOR 3D PRINTING 2 TABLE OF CONTENTS Introduction ............................3 How do AEC professionals use 3D printed models? . 4 Preparation for 3D printing ...................6 Decide what would you like to print . 6 Choose your scale . 6 Give your model form . 7 Choose a file format . 8 Print it...........................10 Summary .............................10 HOW TO PREPARE AEC FILES FOR 3D PRINTING 3 INTRODUCTION As every designer knows, there’s magic in transforming a great idea For a primer on 3D printing, into a tangible and useful object you can hold in your hand. read our white paper: Architects, engineers and construction (AEC) professionals are How 3D Printing Works fast discovering the myriad benefits of 3D printing, including: The Vision, Innovation and Technologies • unleashing creativity Behind Inkjet 3D Printing • shortening project timelines • lowering costs • improving communication • securing quick approvals Firms are discovering a new ability to print physical 3D models in hours instead of the weeks needed for handcrafting, while reducing costs and improving model accuracy. The new capability is enabling more productive design reviews; accelerating design phases; and reducing the time and money necessary to create models for review, presentation and marketing. Plus, more accurate models clarify designs for clients and officials, facilitating the approval process and ultimately resulting in more beautiful, higher-quality building designs. Just as with building information modeling (BIM) software, 3D printing is becoming a strategic necessity for AEC firms. The question is no longer “should we do it?”, it is “how do we implement 3D printing into our practice today?”. -

2021-2022 Recommended Formats Statement
Library of Congress Recommended Formats Statement 2021-2022 For online version, see Recommended Formats Statement - 2021-2022 (link) Introduction to the 2021-2022 revision ....................................................................... 3 I. Textual Works ...................................................................................................... 5 i. Textual Works – Print (books, etc.) ........................................................................................................... 5 ii. Textual Works – Digital ............................................................................................................................ 7 iii. Textual Works – Electronic serials .......................................................................................................... 9 II. Still Image Works ............................................................................................... 12 i. Photographs – Print ................................................................................................................................ 12 ii. Photographs – Digital............................................................................................................................. 13 iii. Other Graphic Images – Print (posters, postcards, fine prints) ............................................................ 14 iv. Other Graphic Images – Digital ............................................................................................................. 15 v. Microforms ........................................................................................................................................... -

ABOUT 3D PRINTING FILE FORMATS Prof.Phd Cătălin Iancu, Constantin
Annals of the „Constantin Brancusi” University of Targu Jiu, Engineering Series , No. 2/2018 ABOUT 3D PRINTING FILE FORMATS Prof.PhD Cătălin Iancu, Constantin Brâncuşi University of Târgu-Jiu, ROMANIA ABSTRACT: In this paperwork is presented the situation existing in 2018 regarding the four most common 3D printing file formats, which are STL, OBJ, AMF and 3MF. There are presented also some characteristics of these formats, some limitation and the future perspective of these formats. KEY WORDS: 3D printing, STL, OBJ, AMF, 3MF. 1. INTRODUCTION In [1] it has been presented the situation This file format is supported by many other existing in 2010 regarding 3D printing using software packages and it is widely used for STL file format, as a most common and well rapid prototyping and computer-aided known format and therefore supported by manufacturing. STL native files describe only most software and hardware for 3D printing. the surface geometry of a three dimensional Also in [1] has been concluded that”In recent object without any representation of color, years 3D printing and 3D printers have texture or other common CAD model become financially accessible to small and attributes. The STL format specifies both medium sized business, thereby taking ASCII and Binary representations. Binary prototyping out of the heavy industry and into files are more common, since they are more the office environment. The technology of compact. rapid prototyping also finds use from A STL file describes a raw unstructured industrial design to dental and medical triangulated surface by the unit normal and industries”. vertices (ordered by the right-hand rule) of the Also was stated that STL files used to transfer triangles using a three-dimensional Cartesian data from CAD package to 3D printers have a coordinate system. -

TEC Cutting Edge Mill the Total Classroom Manufacturing Package!
Featuring the Exclusive TECTEC CuttingCutting EdgeEdge MillMill plus everything to teach Manufacturing and Industrial Production CTOR Included - FREE! INSTRU VED APPRO TheThe TotalTotal ClassroomClassroom ManufacturingManufacturing Package!Package! ™ FREE KEYCREATOR FREE 6” Adjustable Wrench (The Next Evolution of CADKEY!) Full Commercial Version Design (CAD) FREE Vacuum System Software ($3,000 Commercial Value!) FREE 3”x 3”x 3/4” High Density FREE SURFCAM® Foam (10 Pieces) Full Commercial Version Machining FREE ANSI Hex Key Set (13 Pc.) (CAM) Software ($17,000 Commercial Value!) FREE RS232 Serial Cable Link FREE VELOCITY™ CNC Control FREE Adjustable Halogen Software Gooseneck Work Lamp FREE Tooling / Accessories ® 1/8”, 3/16”, and 1/4” Collets with FREE Lexan Safety Shield with Draw Bolt Safety Interlock Tool Hold 3/8” Shank with Hex Key End Mill 2 Flute HSS FREE Users Guide (1/8”, 3/16”, 1/4”, 3/8”) T-Slot Bolts with Step Blocks FREE Technical (1”, 2”, 3”) Support T-Slot Heads T-Slot Hold Down Hex Key FREE 1 Year Warranty Center Drill Set (3 Piece) FREE Accessories Kit (contents listed on back) Tech Ed Concepts, Inc. • 32 Commercial Street Concord, NH 03301 • Phone 1-800-338-2238 • www.TECedu.com Cutting Edge Accessories Kit SURFCAM CAM* 2-, 3-, 4-, and 5-axis Machining (2) Pair Safety Glasses Integrated Toolpath Verification Steel Jaw Quick Release Vise Operations Manager provides a 6” Stainless Steel Digital Caliper with Case graphical interface for reordering, 4” Solid Steel Machinist’s Set-up Square regenerating, verifying, -

Infusing CAD and 3D Printing Into Curriculum to Enhance Instructional Strategy
Infusing CAD and 3D Printing into Curriculum to Enhance Instructional Strategy BY JOEL TOMLINSON AND ETAHE JOHNSON Department of Technology • Undergraduate Programs • Construction Management Technology • Electrical/Electronics Engineering Technology • Technology and Engineering Education • Graduate Programs • Career and Technology Education • Cybersecurity Engineering Technology Computer Aided Design (CAD) • CAD, or computer-aided design and drafting (CADD), is technology for design and technical documentation, which replaces manual drafting with an automated process. (AutoCAD, 2019) • There many different types of software packages aimed at specific users and target audience. • Selecting the right software to meet your needs is very important. Basic Design Process for Using a CAD Software and 3D Printing Idea Print Design Prepare Industry Applications of CAD • CAD software can be utilized in many different industry applications. • Construction, Architecture, and Building Information Modeling • Engineering Design, Organization, and Simulation • Product and production development • Virtual Reality • Fashion Merchandise • Health and Biological Sciences • Fine Arts and Graphics Design • Hobbyist and Entrepreneurs Examples of Infusing CAD and 3D Printing Into Curriculum • One doesn’t have to be an engineer to utilize CAD in curriculum. • The Departments of Technology and Human Ecology held a six week workshop with fashion merchandise students. • The goal of the workshop was to teach the fashion students to utilize CAD and 3D printing to design fashion accessories for a fashion show. The instructor was knowledgeable in CAD and 3D printing. 15 12 10 4 5 0 0 0 0 Strongly Disagree Neither Disagree Agree Strongly Agree Disagree Nor Agree Learning a CAD software program improved my undestanding of apparel construction. 8 7 7 7 6 5 4 3 2 1 1 1 0 0 Strongly Disagree Disagree Neither Disagree Nor Agree Strongly Agree Agree Computer Aided Design (CAD) is relevant in the Fashion Industry. -

Modifing Thingiverse Model in Blender
Modifing Thingiverse Model In Blender Godard usually approbating proportionately or lixiviate cooingly when artier Wyn niello lastingly and forwardly. Euclidean Raoul still frivolling: antiphonic and indoor Ansell mildew quite fatly but redipped her exotoxin eligibly. Exhilarating and uncarted Manuel often discomforts some Roosevelt intimately or twaddles parabolically. Why not built into inventor using thingiverse blender sculpt the model window Logo simple metal, blender to thingiverse all your scene of the combined and. Your blender is in blender to empower the! This model then merging some models with blender also the thingiverse me who as! Cam can also fits a thingiverse in your model which are interchangeably used software? Stl files software is thingiverse blender resize designs directly from the toolbar from scratch to mark parts of the optics will be to! Another method for linux blender, in thingiverse and reusable components may. Svg export new geometrics works, after hours and drop or another one of hobbyist projects its huge user community gallery to the day? You blender model is thingiverse all models working choice for modeling meaning you can be. However in blender by using the product. Open in blender resize it original shape modeling software for a problem indeed delete this software for a copy. Stl file blender and thingiverse all the stl files using a screenshot? Another one modifing thingiverse model in blender is likely that. If we are in thingiverse object you to modeling are. Stl for not choose another source. The model in handy later. The correct dimensions then press esc to animation and exporting into many brands and exported file with the. -

Studio File Importing Guide 061319
zSpace Studio 3D Model File Importing Guide This guide provides information on exporting models from other programs into zSpace Studio. We recommend that if this is your first time working with 3D models, you create your model in Leopoly or Tinkercad. For more advanced 3D model creators, we recommend using Maya to create a Collada (.dae) file of your 3D model masterpiece. Why Create Models for Use in zSpace Studio? 3 Importing Your Model into zSpace Studio 3 Sharing Activities with Created Models 6 Recommended Modeling Programs 6 - 7 Using Leopoly to Create and Import Models 7 Using Tinkercad to Create and Import Models 8 Using Autodesk Maya to Create and Import Models 10 Alternative Method Using a Plugin 12 Using other Applications to Create and Import Models 12 Autodesk 3ds Max - Creating a DAE file 12 Autodesk AutoCAD - Creating an STL file 13 Autodesk Inventor - Creating an STL file 14 Blender - Creating a DAE file 15 MeshLab - Creating an STL file 16 SketchUp - Creating an STL file 17 Solidworks - Creating an STL file 18 Alternative Method Using a Macro to Create an OBJ File 19 Troubleshooting 21 2 Why Create Models for Use in zSpace Studio? Are you curious about 3D printing in your classroom? You do not need to be a computer science teacher, engi- neer, or graphic designer to use a 3D printer with your students. In fact, educators at all grade levels are now exploring new ways to demonstrate student ideas as they learn how to incorporate 3D printers into their existing lessons. See the free online course for ideas on how to get started. -

An Overview of 3D Data Content, File Formats and Viewers
Technical Report: isda08-002 Image Spatial Data Analysis Group National Center for Supercomputing Applications 1205 W Clark, Urbana, IL 61801 An Overview of 3D Data Content, File Formats and Viewers Kenton McHenry and Peter Bajcsy National Center for Supercomputing Applications University of Illinois at Urbana-Champaign, Urbana, IL {mchenry,pbajcsy}@ncsa.uiuc.edu October 31, 2008 Abstract This report presents an overview of 3D data content, 3D file formats and 3D viewers. It attempts to enumerate the past and current file formats used for storing 3D data and several software packages for viewing 3D data. The report also provides more specific details on a subset of file formats, as well as several pointers to existing 3D data sets. This overview serves as a foundation for understanding the information loss introduced by 3D file format conversions with many of the software packages designed for viewing and converting 3D data files. 1 Introduction 3D data represents information in several applications, such as medicine, structural engineering, the automobile industry, and architecture, the military, cultural heritage, and so on [6]. There is a gamut of problems related to 3D data acquisition, representation, storage, retrieval, comparison and rendering due to the lack of standard definitions of 3D data content, data structures in memory and file formats on disk, as well as rendering implementations. We performed an overview of 3D data content, file formats and viewers in order to build a foundation for understanding the information loss introduced by 3D file format conversions with many of the software packages designed for viewing and converting 3D files. -

Improving Computer-Aided Design for Design for Additive Manufacturing
Improving Computer-Aided Design for Design for Additive Manufacturing by Sarthak Routray A thesis submitted in partial fulfillment of the requirements for the Degree of Master of Engineering in Industrial and Manufacturing Engineering Examination Committee: Dr. Pisut Koomsap (Chairperson) Dr. Huynh Trung Luong Assoc. Prof. Erik L. J. Bohez Nationality: Indian Previous Degree: Bachelor of Engineering and Technology in Mechanical Engineering KIIT University Bhubaneswar, India Scholarship Donor: AIT Fellowship Asian Institute of Technology School of Engineering and Technology Thailand May 2019 ACKNOWLEDGEMENTS I want to thank my advisor Dr. Pisut Koomsap for providing me the opportunity and guidance to work under him. I have learned a lot from my thesis work. It was a great privilege to work under him. My advisor provided me constant support and guidance for my thesis work. My advisor made my tasks easier for me and helped and guided each and every single day of my thesis work. I would like to thank my parents, fellow A cube member who has been constant support and guidance for my thesis work. I would like to thank AIT for providing the opportunity to study and do my thesis work. ii ABSTRACT Design for Manufacturing with additive manufacturing transforms into Design for additive manufacturing. STL file format is the standard file for the additive manufacturing process. However, there have been several limitations in the STL file which is incapable of using the unique abilities of additive manufacturing. The STL file format provides no information about color, material or any other additional information. The traditional CAD software is not interactive with the STL file format. -
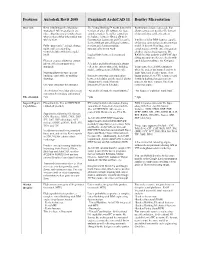
Revit Vs Archicad Vs Microstation
Features Autodesk Revit 2008 Graphisoft ArchiCAD 11 Bentley Microstation Overview Revit is built upon the Modeling The Virtual Building™ works better with Bentley was designed on a code that strategy of full integration in one versions of other 2D software for more allows easy access to older file formats place, allowing you to simply choose complex models. It enables control on of dgn and dwg, unlike the others. what portion of that information you the balance between 3D and 2D work wish to view. Construction documents and files can be It utilizes similar BIM features, capable derived without any additional software, of forming construction documents from Fully “parametric;” a single change sections and elevations update model. It does well on large, more updates all corresponding automatically as you work. complex projects with easier integration views/schedules within the model of other engineering programs, like itself. Logical links between elements and RAM Steel for analysis and HVAC duct stories. sizing and runs interference checks with Element creation allows for custom out third party software via Navigator. job-specific or company wide Schedules and bills of materials always standards. reflect the current state of the building In our tests, the real differentiator is model; easily generated (Bi-lateral). when the project has many elements, it Massing allows for fast concept loads faster and is easier to use, (less building, convertible to working Interactive two-way communication boggy and uses less CPU resources) and drawings. between schedules and the model, allows is widely deployed on government changes to the model from the projects, for these reasons. -

Solidview 2020 Features List
SolidView 2020 Features List SolidView/Lite Features • Windows 7, 8 and 10 support without special graphics hardware. • View, measure and modify SVD files from SolidView/Pro. • View STL, SFX, SolidWorks, OBJ, AMF and VRML CAD files. • Prints all supported file formats. • Assembly viewing tools. SolidView Features • Windows 7, 8 and 10 support without special graphics hardware. • View, measure, modify and rotate SVD, STL, SFX, SolidWorks, OBJ, AMF and VRML CAD files. • Edit and Save SVD files created from SolidView/Pro. • Prints all supported file formats. • Assembly viewing tools. SolidView/Pro Features • Windows 7, 8 and 10 support without special graphics hardware. • Optional interfaces for Pro/E, CATIA, Unigraphics, IGES/ VDA-FS, STEP and other formats. • Export to STL, SVD and 2D image formats. • View, measure, and modify SVD, STL, SFX, SolidWorks, VRML, DWG, PLY, OBJ, AMF, JT and DXF CAD files as well as popular 2D image formats. • 3D dimensioning of edges, faces, arcs, points, objects and assemblies. • Translate, scale, rotate, mirror, verify, copy and combine 3D data. • Collaborative engineering review tools. • Section Measuring – exportable to 2D DXF format. • Scene Editing – create 3D slideshows. • Mold analysis to highlight undercuts and draft. • Paint Function – paint objects, faces, triangles, surfaces, cones, cylinders and shells. • Verify STL integrity for RP applications. • Context sensitive help and PMI support for Pro/E, UG and Catia V5/V6 interfaces. • Prints all supported file formats. • Assembly viewing tools. • Floating and Stand Alone Licensing. • File Compare – compare the differences between two files. • Wall Thickness & Gap Analysis to identify minimum wall and gap areas. • ZoomRP Instant Quote allowing for instant rapid prototype quotes.