DOCSLIB.ORG

Solving the Cubic and Quartic

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Solving the Cubic and Quartic SOLVING THE CUBIC AND QUARTIC AARON LANDESMAN 1. INTRODUCTION Likely you are familiar with how to solve a quadratic equation. Given a quadratic of the form ax2 + bx + c, one can find the two roots in terms of radicals as p -b ± b2 - 4ac . 2a On the other hand, the cubic formula is quite a bit messier. The polynomial x4 + ax3 + bx2 + cx + d has roots . And the quartic formula is messier still. The polynomial x4 + ax3 + bx2 + cx + d has roots v v u r q u r q u 3 3 2 2 3 2 2 2 2 3 p u 3 3 2 2 3 2 2 2 2 3 p 3 b 1 u 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae b2 2c 3 2 c2 - 3bd + 12ae 1 u 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae b2 4c 3 2 c2 - 3bd + 12ae - b + 4cb - 8d x = - - u p + - + - u- p + - - - a3 a2 a 1 u 3 2 r u 3 2 r v r 4a 2 t 3 2a 4a 3a 3 q 2 u 3 2a 2a 3a 3 q u 3 q 2 3 3 2 2 3 2 2 2 2 3 3 2 2 3 2 2 2 2 3 3 2 2 3 2 2 2 3p 3a 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae u 3a 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae u 2c -9bdc-72aec+27ad +27b e+ (2c -9bdc-72aec+27ad +27b e) -4(c -3bd+12ae) 2 2(c2 -3bd+12ae) u u p b 2c 4 3 + 2 - 3a + r t t 3 2a 4a q 2 3 3a 3 2c3 -9bdc-72aec+27ad2 +27b2 e+ (2c3 -9bdc-72aec+27ad2 +27b2 e) -4(c2 -3bd+12ae) v v u r q u r q u 3 3 2 2 3 2 2 2 2 3 p u 3 3 2 2 3 2 2 2 2 3 p 3 b 1 u 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae b2 2c 3 2 c2 - 3bd + 12ae 1 u 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae b2 4c 3 2 c2 - 3bd + 12ae - b + 4cb - 8d x = - - u p + - + + u- p + - - - a3 a2 a 2 u 3 2 r u 3 2 r v r 4a 2 t 3 2a 4a 3a 3 q 2 3 2 u 3 2a 2a 3a 3 q 2 3 u 3 q 2 3 p 3 2 2 3 2 2 2 3 2 2 3 2 2 2 2c3 -9bdc-72aec+27ad2 +27b2 e+ 2c3 -9bdc-72aec+27ad2 +27b2 e -4 c2 -3bd+12ae 3 3a 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae u 3a 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae u ( ) ( ) b2 2c 2(c2 -3bd+12ae) u 4u p + - + r t t 3 3 2a 4a2 3a q 3a 3 2c3 -9bdc-72aec+27ad2 +27b2 e+ (2c3 -9bdc-72aec+27ad2 +27b2 e)2 -4(c2 -3bd+12ae)3 v v u r q u r q u 3 3 2 2 3 2 2 2 2 3 p u 3 3 2 2 3 2 2 2 2 3 p 3 b 1 u 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae b2 2c 3 2 c2 - 3bd + 12ae 1 u 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae b2 4c 3 2 c2 - 3bd + 12ae - b + 4cb - 8d x = - + u p + - + - u- p + - - + a3 a2 a 3 u 3 2 r u 3 2 r v r 4a 2 t 3 2a 4a 3a 3 q 2 3 2 u 3 2a 2a 3a 3 q 2 3 u 3 q 2 3 p 3 2 2 3 2 2 2 3 2 2 3 2 2 2 2c3 -9bdc-72aec+27ad2 +27b2 e+ 2c3 -9bdc-72aec+27ad2 +27b2 e -4 c2 -3bd+12ae 3 3a 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae u 3a 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae u ( ) ( ) b2 2c 2(c2 -3bd+12ae) u 4u p + - + r t t 3 3 2a 4a2 3a q 3a 3 2c3 -9bdc-72aec+27ad2 +27b2 e+ (2c3 -9bdc-72aec+27ad2 +27b2 e)2 -4(c2 -3bd+12ae)3 v v u r q u r q u 3 3 2 2 3 2 2 2 2 3 p u 3 3 2 2 3 2 2 2 2 3 p 3 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae 2 3 2 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae 2 3 2 b 4cb 8d b 1 u b 2c 2 c - 3bd + 12ae 1 u b 4c 2 c - 3bd + 12ae - 3 + 2 - a x = - + u p + - + + u- p + - - + a a . 4 u 3 2 r u 3 2 r v r 4a 2 t 3 2a 4a 3a 3 q 2 3 2 u 3 2a 2a 3a 3 q 2 3 u 3 q 2 3 p 3 2 2 3 2 2 2 3 2 2 3 2 2 2 2c3 -9bdc-72aec+27ad2 +27b2 e+ 2c3 -9bdc-72aec+27ad2 +27b2 e -4 c2 -3bd+12ae 3 3a 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae u 3a 2c - 9bdc - 72aec + 27ad + 27b e + 2c - 9bdc - 72aec + 27ad + 27b e - 4 c - 3bd + 12ae u ( ) ( ) b2 2c 2(c2 -3bd+12ae) u 4u p + - + r t t 3 3 2a 4a2 3a q 3a 3 2c3 -9bdc-72aec+27ad2 +27b2 e+ (2c3 -9bdc-72aec+27ad2 +27b2 e)2 -4(c2 -3bd+12ae)3 Whew! That was a mouthful! No one could possibly be expected to memorize such a monstros- ity. And indeed, no one needs to. We will now explain how you can solve the cubic and quartic equations without the mess. Given a cubic or quartic equation, we will explain how to solve it with pure thought. This should convince you that you could write down the solution in radicals if you wanted to. 1 2 AARON LANDESMAN 2. THE CUBIC EQUATION To start, we explain how one might solve the cubic equation. Suppose we start with an equation of the form x3 + αx2 + βx + γ. We would like to find the roots of this equation. Suppose that over the complex numbers, this factors as (x - a)(x - b)(x - c), and we are looking for values of a, b, and c. Then, we can re-express our above equation as x3 + (-a - b - c)x2 + (ab + bc + ca)x - abc. That is, α = -a - b - c, β = ab + bc + ca, γ = -abc. Observe that α, β, γ are simply the symmetric polynomials in a, b, and c. Let ! be a primitive cube root of unity, i.e., !3 = 1, ! 6= 1. The key to finding a, b, c in terms of radicals is to consider the quantity y := a + !b + !2c. It may seem somewhat unmotivated to consider this quantity, but we will explain in section 4 why one would be naturally let to consider this. For the moment, just bear with us. Let τ be the permutation of the roots sending a 7 b, b 7 c, c 7 a Observe that y satisfies the property that ! ! ! τ(y) := τ(a) + ωτ(b) + !2τ(c) = b + !c + !2a = !2(a + !b + !2c) = !2 · y. Therefore, τ(y3) = (!2)3y3 = y3, and so y3 is fixed by τ. Let σ be the permutation of the roots sending a 7 b, b 7 a, c 7 c. Observe that ! ! ! y6 -(y3 + σ(y3))y3 + σ(y3)y3 = 0, and further that (y3 + σ(y3)) and σ(y3)y3 are both fixed by σ. In particular, these are symmetric polynomials, and hence can be expressed in terms of α, β, γ. Therefore, we can express the above equation as (y3)2 - f(α, β, γ)y3 - g(α, β, γ) = 0. Therefore, y3 satisfies a quadratic equation, and we can use the usual quadratic formula to solve for y3. Then, but taking a cube root, we obtain y. Completely analogously, we can solve for a + !2b + !c SOLVING THE CUBIC AND QUARTIC 3 via radicals in terms of α, β, γ. Since γ = a + b + c, we obtain all three of a + b + c a + !b + !2c a + !2b + !c in terms of radicals. Subtracting the latter two equations from the first, we obtain (1 - !)b + (1 - !2)c (1 - !2)b + (1 - !)c. Then, we can solve for b and c in terms of the above two equations. In some more detail, if we subtract (1 - !) times the second equation from the (1 - !2) times the first, we get (1 - !2)((1 - !)b + (1 - !2)c)-(1 - !)((1 - !2)b + (1 - !)c) = (1 - !2)2c - (1 - !)2 c = (-2!2 + ! + 2! - !2)c = (-3!2 + 3!)c So, dividing this by 3! - 3!2 yields c.
Load more

Recommended publications
  • Symmetry and the Cubic Formula
    SYMMETRY AND THE CUBIC FORMULA DAVID CORWIN The purpose of this talk is to derive the cubic formula. But rather than finding the exact formula, I'm going to prove that there is a cubic formula. The way I'm going to do this uses symmetry in a very elegant way, and it foreshadows Galois theory. Note that this material comes almost entirely from the first chapter of http://homepages.warwick.ac.uk/~masda/MA3D5/Galois.pdf. 1. Deriving the Quadratic Formula Before discussing the cubic formula, I would like to consider the quadratic formula. While I'm expecting you know the quadratic formula already, I'd like to treat this case first in order to motivate what we will do with the cubic formula. Suppose we're solving f(x) = x2 + bx + c = 0: We know this factors as f(x) = (x − α)(x − β) where α; β are some complex numbers, and the problem is to find α; β in terms of b; c. To go the other way around, we can multiply out the expression above to get (x − α)(x − β) = x2 − (α + β)x + αβ; which means that b = −(α + β) and c = αβ. Notice that each of these expressions doesn't change when we interchange α and β. This should be the case, since after all, we labeled the two roots α and β arbitrarily. This means that any expression we get for α should equally be an expression for β. That is, one formula should produce two values. We say there is an ambiguity here; it's ambiguous whether the formula gives us α or β.
    [Show full text]
  • The Diamond Method of Factoring a Quadratic Equation
    The Diamond Method of Factoring a Quadratic Equation Important: Remember that the first step in any factoring is to look at each term and factor out the greatest common factor. For example: 3x2 + 6x + 12 = 3(x2 + 2x + 4) AND 5x2 + 10x = 5x(x + 2) If the leading coefficient is negative, always factor out the negative. For example: -2x2 - x + 1 = -1(2x2 + x - 1) = -(2x2 + x - 1) Using the Diamond Method: Example 1 2 Factor 2x + 11x + 15 using the Diamond Method. +30 Step 1: Multiply the coefficient of the x2 term (+2) and the constant (+15) and place this product (+30) in the top quarter of a large “X.” Step 2: Place the coefficient of the middle term in the bottom quarter of the +11 “X.” (+11) Step 3: List all factors of the number in the top quarter of the “X.” +30 (+1)(+30) (-1)(-30) (+2)(+15) (-2)(-15) (+3)(+10) (-3)(-10) (+5)(+6) (-5)(-6) +30 Step 4: Identify the two factors whose sum gives the number in the bottom quarter of the “x.” (5 ∙ 6 = 30 and 5 + 6 = 11) and place these factors in +5 +6 the left and right quarters of the “X” (order is not important). +11 Step 5: Break the middle term of the original trinomial into the sum of two terms formed using the right and left quarters of the “X.” That is, write the first term of the original equation, 2x2 , then write 11x as + 5x + 6x (the num bers from the “X”), and finally write the last term of the original equation, +15 , to get the following 4-term polynomial: 2x2 + 11x + 15 = 2x2 + 5x + 6x + 15 Step 6: Factor by Grouping: Group the first two terms together and the last two terms together.
    [Show full text]
  • A Quartically Convergent Square Root Algorithm: an Exercise in Forensic Paleo-Mathematics
    A Quartically Convergent Square Root Algorithm: An Exercise in Forensic Paleo-Mathematics David H Bailey, Lawrence Berkeley National Lab, USA DHB’s website: http://crd.lbl.gov/~dhbailey! Collaborator: Jonathan M. Borwein, University of Newcastle, Australia 1 A quartically convergent algorithm for Pi: Jon and Peter Borwein’s first “big” result In 1985, Jonathan and Peter Borwein published a “quartically convergent” algorithm for π. “Quartically convergent” means that each iteration approximately quadruples the number of correct digits (provided all iterations are performed with full precision): Set a0 = 6 - sqrt[2], and y0 = sqrt[2] - 1. Then iterate: 1 (1 y4)1/4 y = − − k k+1 1+(1 y4)1/4 − k a = a (1 + y )4 22k+3y (1 + y + y2 ) k+1 k k+1 − k+1 k+1 k+1 Then ak, converge quartically to 1/π. This algorithm, together with the Salamin-Brent scheme, has been employed in numerous computations of π. Both this and the Salamin-Brent scheme are based on the arithmetic-geometric mean and some ideas due to Gauss, but evidently he (nor anyone else until 1976) ever saw the connection to computation. Perhaps no one in the pre-computer age was accustomed to an “iterative” algorithm? Ref: J. M. Borwein and P. B. Borwein, Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity}, John Wiley, New York, 1987. 2 A quartically convergent algorithm for square roots I have found a quartically convergent algorithm for square roots in a little-known manuscript: · To compute the square root of q, let x0 be the initial approximation.
    [Show full text]
  • Solving Cubic Polynomials
    Solving Cubic Polynomials 1.1 The general solution to the quadratic equation There are four steps to finding the zeroes of a quadratic polynomial. 1. First divide by the leading term, making the polynomial monic. a 2. Then, given x2 + a x + a , substitute x = y − 1 to obtain an equation without the linear term. 1 0 2 (This is the \depressed" equation.) 3. Solve then for y as a square root. (Remember to use both signs of the square root.) a 4. Once this is done, recover x using the fact that x = y − 1 . 2 For example, let's solve 2x2 + 7x − 15 = 0: First, we divide both sides by 2 to create an equation with leading term equal to one: 7 15 x2 + x − = 0: 2 2 a 7 Then replace x by x = y − 1 = y − to obtain: 2 4 169 y2 = 16 Solve for y: 13 13 y = or − 4 4 Then, solving back for x, we have 3 x = or − 5: 2 This method is equivalent to \completing the square" and is the steps taken in developing the much- memorized quadratic formula. For example, if the original equation is our \high school quadratic" ax2 + bx + c = 0 then the first step creates the equation b c x2 + x + = 0: a a b We then write x = y − and obtain, after simplifying, 2a b2 − 4ac y2 − = 0 4a2 so that p b2 − 4ac y = ± 2a and so p b b2 − 4ac x = − ± : 2a 2a 1 The solutions to this quadratic depend heavily on the value of b2 − 4ac.
    [Show full text]
  • Chapter 5 Complex Numbers
    Chapter 5 Complex numbers Why be one-dimensional when you can be two-dimensional? ? 3 2 1 0 1 2 3 − − − ? We begin by returning to the familiar number line, where I have placed the question marks there appear to be no numbers. I shall rectify this by defining the complex numbers which give us a number plane rather than just a number line. Complex numbers play a fundamental rˆolein mathematics. In this chapter, I shall use them to show how e and π are connected and how certain primes can be factorized. They are also fundamental to physics where they are used in quantum mechanics. 5.1 Complex number arithmetic In the set of real numbers we can add, subtract, multiply and divide, but we cannot always extract square roots. For example, the real number 1 has 125 126 CHAPTER 5. COMPLEX NUMBERS the two real square roots 1 and 1, whereas the real number 1 has no real square roots, the reason being that− the square of any real non-zero− number is always positive. In this section, we shall repair this lack of square roots and, as we shall learn, we shall in fact have achieved much more than this. Com- plex numbers were first studied in the 1500’s but were only fully accepted and used in the 1800’s. Warning! If r is a positive real number then √r is usually interpreted to mean the positive square root. If I want to emphasize that both square roots need to be considered I shall write √r.
    [Show full text]
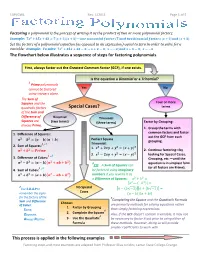
  • Factoring Polynomials
    EAP/GWL Rev. 1/2011 Page 1 of 5 Factoring a polynomial is the process of writing it as the product of two or more polynomial factors. Example: — Set the factors of a polynomial equation (as opposed to an expression) equal to zero in order to solve for a variable: Example: To solve ,; , The flowchart below illustrates a sequence of steps for factoring polynomials. First, always factor out the Greatest Common Factor (GCF), if one exists. Is the equation a Binomial or a Trinomial? 1 Prime polynomials cannot be factored Yes No using integers alone. The Sum of Squares and the Four or more quadratic factors Special Cases? terms of the Sum and Difference of Binomial Trinomial Squares are (two terms) (three terms) Factor by Grouping: always Prime. 1. Group the terms with common factors and factor 1. Difference of Squares: out the GCF from each Perfe ct Square grouping. 1 , 3 Trinomial: 2. Sum of Squares: 1. 2. Continue factoring—by looking for Special Cases, 1 , 2 2. 3. Difference of Cubes: Grouping, etc.—until the 3 equation is in simplest form FYI: A Sum of Squares can 1 , 2 (or all factors are Prime). 4. Sum of Cubes: be factored using imaginary numbers if you rewrite it as a Difference of Squares: — 2 Use S.O.A.P to No Special √1 √1 Cases remember the signs for the factors of the 4 Completing the Square and the Quadratic Formula Sum and Difference Choose: of Cubes: are primarily methods for solving equations rather 1. Factor by Grouping than simply factoring expressions.
    [Show full text]
  • Math: Honors Geometry UNIT/Weeks (Not Timeline/Topics Essential Questions Consecutive)
    Math: Honors Geometry UNIT/Weeks (not Timeline/Topics Essential Questions consecutive) Reasoning and Proof How can you make a Patterns and Inductive Reasoning conjecture and prove that it is Conditional Statements 2 true? Biconditionals Deductive Reasoning Reasoning in Algebra and Geometry Proving Angles Congruent Congruent Triangles How do you identify Congruent Figures corresponding parts of Triangle Congruence by SSS and SAS congruent triangles? Triangle Congruence by ASA and AAS How do you show that two 3 Using Corresponding Parts of Congruent triangles are congruent? Triangles How can you tell whether a Isosceles and Equilateral Triangles triangle is isosceles or Congruence in Right Triangles equilateral? Congruence in Overlapping Triangles Relationships Within Triangles Mid segments of Triangles How do you use coordinate Perpendicular and Angle Bisectors geometry to find relationships Bisectors in Triangles within triangles? 3 Medians and Altitudes How do you solve problems Indirect Proof that involve measurements of Inequalities in One Triangle triangles? Inequalities in Two Triangles How do you write indirect proofs? Polygons and Quadrilaterals How can you find the sum of The Polygon Angle-Sum Theorems the measures of polygon Properties of Parallelograms angles? Proving that a Quadrilateral is a Parallelogram How can you classify 3.2 Properties of Rhombuses, Rectangles and quadrilaterals? Squares How can you use coordinate Conditions for Rhombuses, Rectangles and geometry to prove general Squares
    [Show full text]
  • Quadratic Equations Through History
    Cal McKeever & Robert Bettinger COMMON CORE STANDARD 3B Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression. Factor a quadratic expression to reveal the zeros of the function it defines. Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines. SYNOPSIS At a summit of time-traveling historical mathematicians, attendees from Ancient Babylon pose the question of how to solve quadratic equations. Their method of completing the square serves their purposes, but there was far more to be done with this complex equation. Pythagoras, Euclid, Brahmagupta, Bhaskara II, Al-Khwarizmi and Descartes join the discussion, each pointing out their contributions to the contemporary understanding of solving quadratics through the quadratic formula. Through their discussion, the historical situation through which we understand the solving of quadratic equations is highlighted, showing the complex history of this formula taught everywhere. As the target audience for this project is high school students, the different characters of the script use language and symbolism that is anachronistic but will help the the students to understand the concepts that are discussed. For example, Diophantus did not use a,b,c in his actual texts but his fictional character in the the given script does explain his method of solving quadratics using contemporary notation. HISTORICAL BACKGROUND The problem of solving quadratic equations dates back to Babylonia in the 2nd Millennium BC. The Babylonian understanding of quadratics was used geometrically, to solve questions of area with real-world solutions.
    [Show full text]
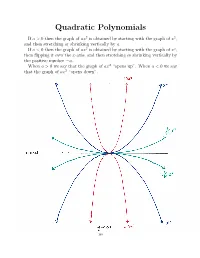
  • Quadratic Polynomials
    Quadratic Polynomials If a>0thenthegraphofax2 is obtained by starting with the graph of x2, and then stretching or shrinking vertically by a. If a<0thenthegraphofax2 is obtained by starting with the graph of x2, then flipping it over the x-axis, and then stretching or shrinking vertically by the positive number a. When a>0wesaythatthegraphof− ax2 “opens up”. When a<0wesay that the graph of ax2 “opens down”. I Cit i-a x-ax~S ~12 *************‘s-aXiS —10.? 148 2 If a, c, d and a = 0, then the graph of a(x + c) 2 + d is obtained by If a, c, d R and a = 0, then the graph of a(x + c)2 + d is obtained by 2 R 6 2 shiftingIf a, c, the d ⇥ graphR and ofaax=⇤ 2 0,horizontally then the graph by c, and of a vertically(x + c) + byd dis. obtained (Remember by shiftingshifting the the⇥ graph graph of of axax⇤ 2 horizontallyhorizontally by by cc,, and and vertically vertically by by dd.. (Remember (Remember thatthatd>d>0meansmovingup,0meansmovingup,d<d<0meansmovingdown,0meansmovingdown,c>c>0meansmoving0meansmoving thatleft,andd>c<0meansmovingup,0meansmovingd<right0meansmovingdown,.) c>0meansmoving leftleft,and,andc<c<0meansmoving0meansmovingrightright.).) 2 If a =0,thegraphofafunctionf(x)=a(x + c) 2+ d is called a parabola. If a =0,thegraphofafunctionf(x)=a(x + c)2 + d is called a parabola. 6 2 TheIf a point=0,thegraphofafunction⇤ ( c, d) 2 is called thefvertex(x)=aof(x the+ c parabola.) + d is called a parabola. The point⇤ ( c, d) R2 is called the vertex of the parabola.
    [Show full text]
  • The Quadratic Formula You May Recall the Quadratic Formula for Roots of Quadratic Polynomials Ax2 + Bx + C
    For example, when we take the polynomial f (x) = x2 − 3x − 4, we obtain p 3 ± 9 + 16 2 which gives 4 and −1. Some quick terminology 2 I We say that 4 and −1 are roots of the polynomial x − 3x − 4 or solutions to the polynomial equation x2 − 3x − 4 = 0. 2 I We may factor x − 3x − 4 as (x − 4)(x + 1). 2 I If we denote x − 3x − 4 as f (x), we have f (4) = 0 and f (−1) = 0. The quadratic formula You may recall the quadratic formula for roots of quadratic polynomials ax2 + bx + c. It says that the solutions to this polynomial are p −b ± b2 − 4ac : 2a Some quick terminology 2 I We say that 4 and −1 are roots of the polynomial x − 3x − 4 or solutions to the polynomial equation x2 − 3x − 4 = 0. 2 I We may factor x − 3x − 4 as (x − 4)(x + 1). 2 I If we denote x − 3x − 4 as f (x), we have f (4) = 0 and f (−1) = 0. The quadratic formula You may recall the quadratic formula for roots of quadratic polynomials ax2 + bx + c. It says that the solutions to this polynomial are p −b ± b2 − 4ac : 2a For example, when we take the polynomial f (x) = x2 − 3x − 4, we obtain p 3 ± 9 + 16 2 which gives 4 and −1. 2 I We may factor x − 3x − 4 as (x − 4)(x + 1). 2 I If we denote x − 3x − 4 as f (x), we have f (4) = 0 and f (−1) = 0.
    [Show full text]
  • A Historical Survey of Methods of Solving Cubic Equations Minna Burgess Connor
    University of Richmond UR Scholarship Repository Master's Theses Student Research 7-1-1956 A historical survey of methods of solving cubic equations Minna Burgess Connor Follow this and additional works at: http://scholarship.richmond.edu/masters-theses Recommended Citation Connor, Minna Burgess, "A historical survey of methods of solving cubic equations" (1956). Master's Theses. Paper 114. This Thesis is brought to you for free and open access by the Student Research at UR Scholarship Repository. It has been accepted for inclusion in Master's Theses by an authorized administrator of UR Scholarship Repository. For more information, please contact [email protected]. A HISTORICAL SURVEY OF METHODS OF SOLVING CUBIC E<~UATIONS A Thesis Presented' to the Faculty or the Department of Mathematics University of Richmond In Partial Fulfillment ot the Requirements tor the Degree Master of Science by Minna Burgess Connor August 1956 LIBRARY UNIVERStTY OF RICHMOND VIRGlNIA 23173 - . TABLE Olf CONTENTS CHAPTER PAGE OUTLINE OF HISTORY INTRODUCTION' I. THE BABYLONIANS l) II. THE GREEKS 16 III. THE HINDUS 32 IV. THE CHINESE, lAPANESE AND 31 ARABS v. THE RENAISSANCE 47 VI. THE SEVEW.l'EEl'iTH AND S6 EIGHTEENTH CENTURIES VII. THE NINETEENTH AND 70 TWENTIETH C:BNTURIES VIII• CONCLUSION, BIBLIOGRAPHY 76 AND NOTES OUTLINE OF HISTORY OF SOLUTIONS I. The Babylonians (1800 B. c.) Solutions by use ot. :tables II. The Greeks·. cs·oo ·B.c,. - )00 A~D.) Hippocrates of Chios (~440) Hippias ot Elis (•420) (the quadratrix) Archytas (~400) _ .M~naeobmus J ""375) ,{,conic section~) Archimedes (-240) {conioisections) Nicomedea (-180) (the conchoid) Diophantus ot Alexander (75) (right-angled tr~angle) Pappus (300) · III.
    [Show full text]
  • Positivity Conditions for Cubic, Quartic and Quintic Polynomials Arxiv:2008.10922V10 [Math.GM] 18 Sep 2020
    Positivity Conditions for Cubic, Quartic and Quintic Polynomials Liqun Qi,∗ Yisheng Song,y and Xinzhen Zhang,z August 17, 2021 Abstract We present a necessary and sufficient condition for a cubic polynomial to be positive for all positive reals. We identify the set where the cubic polynomial is nonnegative but not all positive for all positive reals, and explicitly give the points where the cubic polynomial attains zero. We then reformulate a necessary and sufficient condition for a quartic polynomial to be nonnegative for all posi- tive reals. From this, we derive a necessary and sufficient condition for a quartic polynomial to be nonnegative and positive for all reals. Our condition explic- itly exhibits the scope and role of some coefficients, and has strong geometrical meaning. In the interior of the nonnegativity region for all reals, there is an ap- pendix curve. The discriminant is zero at the appendix, and positive in the other part of the interior of the nonnegativity region. By using the Sturm sequences, we present a necessary and sufficient condition for a quintic polynomial to be positive and nonnegative for all positive reals. We show that for polynomials of a fixed even degree higher than or equal to four, if they have no real roots, then their discriminants take the same sign, which depends upon that degree only, except on an appendix set of dimension lower by two, where the discriminants attain zero. arXiv:2008.10922v10 [math.GM] 18 Sep 2020 Key words. Cubic polynomials, quartic polynomials, quintic polynomials, the Sturm theorem, discriminant, appendix. AMS subject classifications.
    [Show full text]