Solitons in Nonlinear Lattices
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Aitken Basin
Geological and geochemical analysis of units in the South Pole – Aitken Basin A.M. Borst¹,², F.S. Bexkens¹,², B. H. Foing², D. Koschny² ¹ Department of Petrology, VU University Amsterdam ² SCI-S. Research and Scientific Support Department, ESA – ESTEC Student Planetary Workshop 10-10-2008 ESA/ESTEC The Netherlands The South Pole – Aitken Basin Largest and oldest Lunar impact basin - Diameter > 2500 km - Depth > 12 km - Age 4.2 - 3.9 Ga Formed during Late heavy bombardment? Window into the interior and evolution of the Moon Priority target for future sample return missions Digital Elevation Model from Clementine altimetry data. Produced in ENVI, 50x vertical exaggeration, orthographic projection centered on the far side. Red +10 km, purple/black -10km. (A.M.Borst et.al. 2008) 1 The Moon and the SPA Basin Geochemistry Iron map South Pole – Aitken Basin mafic anomaly • High Fe, Th, Ti and Mg abundances • Excavation of mafic deep crustal / upper mantle material Thorium map Clementine 750 nm albedo map from USGS From Paul Lucey, J. Geophys. Res., 2000 Map-a-Planet What can we learn from the SPA Basin? • Large impacts; Implications and processes • Volcanism; Origin, age and difference with near side mare basalts • Cratering record; Age, frequency and size distribution • Late Heavy Bombardment; Intensity, duration and origin • Composition of the deeper crust and possibly upper mantle 2 Topics of SPA Basin study 1) Global structure of the basin (F.S. Bexkens et al, 2008) • Rims, rings, ejecta distribution, subsequent craters modifications, reconstructive -

Ices on Mercury: Chemistry of Volatiles in Permanently Cold Areas of Mercury’S North Polar Region
Icarus 281 (2017) 19–31 Contents lists available at ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus Ices on Mercury: Chemistry of volatiles in permanently cold areas of Mercury’s north polar region ∗ M.L. Delitsky a, , D.A. Paige b, M.A. Siegler c, E.R. Harju b,f, D. Schriver b, R.E. Johnson d, P. Travnicek e a California Specialty Engineering, Pasadena, CA b Dept of Earth, Planetary and Space Sciences, University of California, Los Angeles, CA c Planetary Science Institute, Tucson, AZ d Dept of Engineering Physics, University of Virginia, Charlottesville, VA e Space Sciences Laboratory, University of California, Berkeley, CA f Pasadena City College, Pasadena, CA a r t i c l e i n f o a b s t r a c t Article history: Observations by the MESSENGER spacecraft during its flyby and orbital observations of Mercury in 2008– Received 3 January 2016 2015 indicated the presence of cold icy materials hiding in permanently-shadowed craters in Mercury’s Revised 29 July 2016 north polar region. These icy condensed volatiles are thought to be composed of water ice and frozen Accepted 2 August 2016 organics that can persist over long geologic timescales and evolve under the influence of the Mercury Available online 4 August 2016 space environment. Polar ices never see solar photons because at such high latitudes, sunlight cannot Keywords: reach over the crater rims. The craters maintain a permanently cold environment for the ices to persist. Mercury surface ices magnetospheres However, the magnetosphere will supply a beam of ions and electrons that can reach the frozen volatiles radiolysis and induce ice chemistry. -

Conventional Soliton and Noise-Like Pulse Generated in an Er-Doped Fiber Laser with Carbon Nanotube Saturable Absorbers
applied sciences Article Conventional Soliton and Noise-Like Pulse Generated in an Er-Doped Fiber Laser with Carbon Nanotube Saturable Absorbers Zikai Dong 1, Jinrong Tian 1, Runlai Li 2 , Youshuo Cui 1, Wenhai Zhang 3 and Yanrong Song 1,* 1 College of Applied Sciences, Beijing University of Technology, Beijing 100124, China; [email protected] (Z.D.); [email protected] (J.T.); [email protected] (Y.C.) 2 Department of Chemistry, National University of Singapore, Singapore 637551, Singapore; [email protected] 3 College of Environment and Energy Engineering, Beijing University of Technology, Beijing 100124, China; [email protected] * Correspondence: [email protected] Received: 6 July 2020; Accepted: 27 July 2020; Published: 11 August 2020 Featured Application: Multi-functional ultrafast laser sources, conventional soliton and noise-like pulse laser system, nanomaterial saturable absorption effect test system. Abstract: Conventional soliton (CS) and noise-like pulse (NLP) are two different kinds of pulse regimes in ultrafast fiber lasers, which have many intense applications. In this article, we experimentally demonstrate that the pulse regime of an Er-doped fiber laser could be converted between conventional soliton and noise-like pulse by using fast response saturable absorbers (SA) made from different layers of single-wall carbon nanotubes (CNT). For the monolayer (ML) single-wall CNT-SA, CS with pulse duration of 439 fs at 1560 nm is achieved while for the bilayer (BL) single-wall CNT, NLP at 1560 nm with a 1.75 ps spike and a 98 ps pedestal is obtained. The transition mechanism from CS to NLP is investigated by analyzing the optical characteristics of ML and BL single-wall CNT. -

Geologic Gems of California's State Parks
STATE OF CALIFORNIA – EDMUND G. BROWN JR., GOVERNOR NATURAL RESOURCES AGENCY – JOHN LAIRD, SECRETARY CALIFORNIA GEOLOGICAL SURVEY DEPARTMENT OF PARKS AND RECREATION – LISA MANGAT, DIRECTOR JOHN D. PARRISH, Ph.D., STATE GEOLOGIST DEPARTMENT OF CONSERVATION – DAVID BUNN, DIRECTOR PLATE 1 The rugged cliffs of Del Norte Coast Redwoods State Park are composed of some of California’s Bio-regions the most tortured, twisted, and mobile rocks of the North American continent. The California’s Geomorphic Provinces rocks are mostly buried beneath soils and covered by vigorous redwood forests, which thrive in a climate famous for summer fog and powerful winter storms. The rocks only reveal themselves in steep stream banks, along road and trail cut banks, along the precipitous coastal cliffs and offshore in the form of towering rock monuments or sea stacks. (Photograph by CalTrans staff.) Few of California’s State parks display impressive monoliths adorned like a Patrick’s Point State Park displays a snapshot of geologic processes that have castle with towering spires and few permit rock climbing. Castle Crags State shaped the face of western North America, and that continue today. The rocks Park is an exception. The scenic beauty is best enjoyed from a distant exposed in the seacliffs and offshore represent dynamic interplay between the vantage point where one can see the range of surrounding landforms. The The Klamath Mountains consist of several rugged ranges and deep canyons. Klamath/North Coast Bioregion San Joaquin Valley Colorado Desert subducting oceanic tectonic plate (Gorda Plate) and the continental North American monolith and its surroundings are a microcosm of the Klamath Mountains The mountains reach elevations of 6,000 to 8,000 feet. -

Real-Time Observation of Dissipative Soliton Formation in Nonlinear Polarization Rotation Mode- Locked fibre Lasers
ARTICLE DOI: 10.1038/s42005-018-0022-7 OPEN Real-time observation of dissipative soliton formation in nonlinear polarization rotation mode- locked fibre lasers Junsong Peng1, Mariia Sorokina2, Srikanth Sugavanam2, Nikita Tarasov2,3, Dmitry V. Churkin3, 1234567890():,; Sergei K. Turitsyn2,3 & Heping Zeng1 Formation of coherent structures and patterns from unstable uniform state or noise is a fundamental physical phenomenon that occurs in various areas of science ranging from biology to astrophysics. Understanding of the underlying mechanisms of such processes can both improve our general interdisciplinary knowledge about complex nonlinear systems and lead to new practical engineering techniques. Modern optics with its high precision mea- surements offers excellent test-beds for studying complex nonlinear dynamics, though capturing transient rapid formation of optical solitons is technically challenging. Here we unveil the build-up of dissipative soliton in mode-locked fibre lasers using dispersive Fourier transform to measure spectral dynamics and employing autocorrelation analysis to investi- gate temporal evolution. Numerical simulations corroborate experimental observations, and indicate an underlying universality in the pulse formation. Statistical analysis identifies cor- relations and dependencies during the build-up phase. Our study may open up possibilities for real-time observation of various nonlinear structures in photonic systems. 1 State Key Laboratory of Precision Spectroscopy, East China Normal University, 200062 Shanghai, -

Study of Acoustic Cavitation Near Metal Surfaces Contaminated by Uranium Ran Ji
Study of acoustic cavitation near metal surfaces contaminated by uranium Ran Ji To cite this version: Ran Ji. Study of acoustic cavitation near metal surfaces contaminated by uranium. Other. Université Montpellier, 2018. English. NNT : 2018MONTS131. tel-02282007 HAL Id: tel-02282007 https://tel.archives-ouvertes.fr/tel-02282007 Submitted on 9 Sep 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. THÈ SE POUR OBTENIR LE GRADE DE DOCTEUR DE L’UNIVERSITÉ DE MONTPELLIER En Chimie Sé parative - Maté riaux et Procé dé s É cole doctorale Sciences Chimiques Balard (ED 459) Unité de recherche Institut de Chimie Sé parative de Marcoule (UMR 5257) Study of Acoustic Cavitation near Metal Surfaces Contaminated by Uranium Pré senté e par Ran JI Le 13 novembre 2018 Sous la direction de Sergueï NIKITENKO Rapport de gestion Devant le jury composé de [Jean-Franç ois DUFÊ CHE, Prof, Université Montpellier] [Pré sident] [Jean-Yves HIHN, Prof, Université de Franche-Comté ] [Rapporteur] 2015 [Laurie BARTHE, MCF, INP Toulouse] [Rapporteur] [Sergueï NIKITENKO, DR, CNRS Montpellier] [Directeur de Thè se] [Claire LE NAOUR, CR, Université Paris Saclay] [Examinateur] [Micheline DRAYE, Prof, Université Savoie Mont Blanc] [Examinateur] [Rachel PFLIEGER, CR, CEA Marcoule] [Encadrant] [Matthieu VIROT, CR, CEA Marcoule] [Encadrant] [Pascal PILUSO, CR, CEA Cadarache] [Invité ] “The unity of inner knowledge and action” [Wang Yangming] Acknowledgements Acknowledgements The doctoral study of the past three years has greatly enriched my experience in academic and personal life. -

March 21–25, 2016
FORTY-SEVENTH LUNAR AND PLANETARY SCIENCE CONFERENCE PROGRAM OF TECHNICAL SESSIONS MARCH 21–25, 2016 The Woodlands Waterway Marriott Hotel and Convention Center The Woodlands, Texas INSTITUTIONAL SUPPORT Universities Space Research Association Lunar and Planetary Institute National Aeronautics and Space Administration CONFERENCE CO-CHAIRS Stephen Mackwell, Lunar and Planetary Institute Eileen Stansbery, NASA Johnson Space Center PROGRAM COMMITTEE CHAIRS David Draper, NASA Johnson Space Center Walter Kiefer, Lunar and Planetary Institute PROGRAM COMMITTEE P. Doug Archer, NASA Johnson Space Center Nicolas LeCorvec, Lunar and Planetary Institute Katherine Bermingham, University of Maryland Yo Matsubara, Smithsonian Institute Janice Bishop, SETI and NASA Ames Research Center Francis McCubbin, NASA Johnson Space Center Jeremy Boyce, University of California, Los Angeles Andrew Needham, Carnegie Institution of Washington Lisa Danielson, NASA Johnson Space Center Lan-Anh Nguyen, NASA Johnson Space Center Deepak Dhingra, University of Idaho Paul Niles, NASA Johnson Space Center Stephen Elardo, Carnegie Institution of Washington Dorothy Oehler, NASA Johnson Space Center Marc Fries, NASA Johnson Space Center D. Alex Patthoff, Jet Propulsion Laboratory Cyrena Goodrich, Lunar and Planetary Institute Elizabeth Rampe, Aerodyne Industries, Jacobs JETS at John Gruener, NASA Johnson Space Center NASA Johnson Space Center Justin Hagerty, U.S. Geological Survey Carol Raymond, Jet Propulsion Laboratory Lindsay Hays, Jet Propulsion Laboratory Paul Schenk, -

Stochastic and Higher-Order Effects on Exploding Pulses
Article Stochastic and Higher-Order Effects on Exploding Pulses Orazio Descalzi * and Carlos Cartes Complex Systems Group, Facultad de Ingeniería y Ciencias Aplicadas, Universidad de los Andes, Av. Mons. Álvaro del Portillo 12.455, Las Condes, Santiago 7620001, Chile; [email protected] * Correspondence: [email protected] Received: 27 June 2017; Accepted: 22 July 2017; Published: 30 August 2017 Abstract: The influence of additive noise, multiplicative noise, and higher-order effects on exploding solitons in the framework of the prototype complex cubic-quintic Ginzburg-Landau equation is studied. Transitions from explosions to filling-in to the noisy spatially homogeneous finite amplitude solution, collapse (zero solution), and periodic exploding dissipative solitons are reported. Keywords: exploding solitons; Ginzburg-Landau equation; mode-locked fiber lasers 1. Introduction Soliton explosions, fascinating nonlinear phenomena in dissipative systems, have been observed in at least three key experiments. As has been reported by Cundiff et al. [1], a mode-locked laser using a Ti:Sapphire crystal can produce intermittent explosions. More recently, a different medium for explosions was reported by Broderick et al., namely, a passively mode-locked fibre laser [2]. In 2016, Liu et al. showed that in an ultrafast fiber laser, the exploding behavior could operate in a sustained but periodic mode called “successive soliton explosions” [3]. Almost all parts of these exploding objects are unstable, but nevertheless they remain localized. Localized structures in systems far from equilibrium are the result of a delicate balance between injection and dissipation of energy, nonlinearity and dispersion (compare [4] for a recent exposition of the subject). This fact leads to a generalization of the well known conservative soliton to a dissipative soliton DS (Akhmediev et al. -

Dissipative Soliton Interactions Inside a Fiber Laser Cavity
Optical Fiber Technology 11 (2005) 209–228 www.elsevier.com/locate/yofte Invited paper Dissipative soliton interactions inside a fiber laser cavity N. Akhmediev a,∗, J.M. Soto-Crespo b, M. Grapinet c, Ph. Grelu c a Optical Sciences Group, RSPhysSE, ANU, ACT 0200, Australia b Instituto de Óptica, CSIC, Serrano 121, 28006 Madrid, Spain c Laboratoire de Physique de l’Université de Bourgogne, Unité Mixte de Recherche 5027 du Centre National de Recherche Scientifique, B.P. 47870, 21078 Dijon, France Received 9 December 2004 Available online 22 April 2005 Abstract We report our recent numerical and experimental observations of dissipative soliton interactions inside a fiber laser cavity. A bound state, formed from two pulses, may have a group velocity which differs from that of a single soliton. As a result, they can collide inside the cavity. This results in a variety of outcomes. Numerical simulations are based either on a continuous model or on a parameter-managed model of the cubic-quintic Ginzburg–Landau equation. Each of the models pro- vides explanations for our experimental observations. 2005 Elsevier Inc. All rights reserved. Keywords: Soliton 1. Introduction Soliton interaction is one of the most exciting areas of research in nonlinear dynam- ics. The unusual features of collisions in systems described by the Korteweg–de Vries (KdV) equation [1] were the starting point of these intensive studies. It was discovered that solitons in this system pass through each other without changing their amplitude and * Corresponding author. E-mail address: [email protected] (N. Akhmediev). 1068-5200/$ – see front matter 2005 Elsevier Inc. -

Twenty-Five Years of Dissipative Solitons
Twenty-Five Years of Dissipative Solitons Ivan C. Christova) and Zongxin Yub) School of Mechanical Engineering, Purdue University, West Lafayette, Indiana 47907, USA Abstract. In 1995, C. I. Christov and M. G. Velarde introduced the concept of a dissipative soliton in a long-wave thin-film equation [Physica D 86, 323–347]. In the 25 years since, the subject has blossomed to include many related phenomena. The focus of this short note is to survey the conceptual influence of the concept of a “production-dissipation (input-output) energy balance” that they identified. Our recent results on nonlinear periodic waves as dissipative solitons (in a model equation for a ferrofluid interface in a parallel-flow rectangular geometry subject to an inhomogeneous magnetic field) have shown that the classical concept also applies to nonlocalized (specifically, spatially periodic) nonlinear coherent structures. Thus, we revisit the so-called KdV-KSV equation studied by C. I. Christov and M. G. Velarde to demonstrate that it also possesses spatially periodic dissipative soliton solutions. These coherent structures arise when the linearly unstable flat film state evolves to sufficiently large amplitude. The linear instability is then arrested when the nonlinearity saturates, leading to permanent traveling waves. Although the two model equations considered in this short note feature the same prototypical linear long-wave instability mechanism, along with similar linear dispersion, their nonlinearities are fundamentally different. These nonlinear terms set the shape and eventual dynamics of the nonlinear periodic waves. Intriguingly, the nonintegrable equations discussed in this note also exhibit multiperiodic nonlinear wave solutions, akin to the polycnoidal waves discussed by J. -
![Arxiv:1003.0154V1 [Physics.Atom-Ph] 28 Feb 2010 SWCNT Mode Lockers Have the Advantages Such As In- with Large Normal Cavity Dispersion8,9](https://docslib.b-cdn.net/cover/7954/arxiv-1003-0154v1-physics-atom-ph-28-feb-2010-swcnt-mode-lockers-have-the-advantages-such-as-in-with-large-normal-cavity-dispersion8-9-837954.webp)
Arxiv:1003.0154V1 [Physics.Atom-Ph] 28 Feb 2010 SWCNT Mode Lockers Have the Advantages Such As In- with Large Normal Cavity Dispersion8,9
Graphene mode locked, wavelength-tunable, dissipative soliton fiber laser Han Zhang,1 Dingyuan Tang,1;∗ R. J. Knize,,2 Luming Zhao,1 Qiaoliang Bao,3 and Kian Ping Loh ,31 1School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore 639798 2Department of Physics, United States Air Force Academy, Colorado 80840, United States of America 3Department of Chemistry, National University of Singapore, Singapore 117543 ∗Corresponding author: [email protected], [email protected] a) (Dated: February 2010; Revised 22 October 2018) CONTENTS made. A wideband wavelength tunable erbium-doped fiber laser mode locked with SWCNTs was experimen- 2 I. Introduction 1 tally demonstrated . A. Nanotube Mode-Locked Fiber Laser1 B. Drawback of Nanotube Mode-Locker1 C. Soliton Fiber Laser1 B. Drawback of Nanotube Mode-Locker D. Graphene Mode-Locked Fiber Laser2 However, the broadband SWCNT mode locker suffers II. Experimental studies 2 intrinsic drawbacks: SWCNTs with a certain diameter only contribute to the saturable absorption of a particu- III. Conclusion 4 lar wavelength of light, and SWCNTs tend to form bun- dles that finish up as scattering sites. Therefore, coex- IV. Acknowledgement 4 istence of SWCNTs with different diameters introduces extra linear losses to the mode locker, making mode lock- V. Citations and References 4 ing of a laser difficult to achieve. In this letter we show that these drawbacks could be circumvented if graphene is used as a broadband saturable absorber. Implementing I. INTRODUCTION graphene mode locking in a specially designed erbium- doped fiber laser, we demonstrated the first wide range Atomic layer graphene possesses wavelength- (1570nm- 1600nm) wavelength tunable dissipative soliton insensitive ultrafast saturable absorption, which fiber laser. -
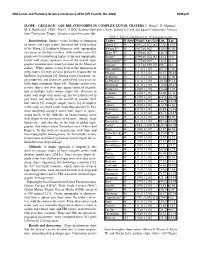
Slope - Geologic Age Relationships in Complex Lunar Craters C
49th Lunar and Planetary Science Conference 2018 (LPI Contrib. No. 2083) 2399.pdf SLOPE - GEOLOGIC AGE RELATIONSHIPS IN COMPLEX LUNAR CRATERS C. Rojas1, P. Mahanti1, M. S. Robinson1, LROC Team1, 1LROC Science Operation Center, School of Earth and Space Exploration, Arizona State University, Tempe, Arizona ([email protected]) Table 1: List of complex craters. *Copernican craters Introduction: Impact events leading to formation Crater D (km) Model Age (Ga) Lon Lat of basins and large craters dominate the early history Moore F* 24 0.041∓0.012 [8] 37.30 185.0 of the Moon [1] leading to kilometer scale topographic Wiener F* 30 0.017∓0.002 149.9740.90 variations on the lunar surface, with smaller crater [2], Klute W* 31 0.090∓0.007 216.7037.98 progressively introducing higher frequency topography. Necho* 37 0.080∓0.024 [8] 123.3 –5.3 Crater wall slopes represent most of the overall topo- Aristarchus* 40 0.175∓0.0095 312.5 23.7 graphic variation since many locations on the Moon are Jackson* 71 0.147∓0.038 [9] 196.7 22.1 craters. While impact events lead to the formation of McLaughlin 75 3.7∓0.1 [10] 267.1747.01 steep slopes [3], they are also primarily responsible for Pitiscus 80 3.8∓0.1 [10] 30.57 -50.61 landform degradation [4]. During crater formation, tar- Al-Biruni 80 3.8∓0.1 [10] 92.62 18.09 get properties and processes controlling structural sta- La Pérouse 80 3.6∓0.1 [10] -10.66 76.18 bility limit maximum slopes [4].