Ptolemy's World Map and Eratosthenes's Circumference Of
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Analyze a World Map
Analyze a World Map Materials: Map of the World: Political or use link this website Map of the World Worksheet You could start the discussion by saying that the social studies part of the GED test assumes that everyone has a basic knowledge of world geography. The test will contain maps that you have to analyze and the answers are not always directly on the map. This is one area of the test where they expect you to just know the approximate locations of countries and oceans. So we thought we would use this world map to familiarize everyone with some world geography. Hand out the maps. The first thing you need to do with a map is read the title so that you know what you are looking at. Ask, “What is the title of this map?” ‘Map of the World: Political”. So this map should give us information about the location of countries. Then look to see if there is a legend or a list of symbols that explains the information shown on the map. Ask, “Is there a legend for this map/” Yes, it shows the scale of the map. You can discuss that the scale shows the relationship between distances on the map to the actual distance on the ground. Look to see if there is anything on the map showing directions, most maps have a compass that shows east, west, north, and south. Ask, “Does this map have any symbols indicating direction?” Yes, this map has a direction compass that shows points north. Ask if students know where south, east, and west are on the map. -

Countries and Continents of the World: a Visual Model
Countries and Continents of the World http://geology.com/world/world-map-clickable.gif By STF Members at The Crossroads School Africa Second largest continent on earth (30,065,000 Sq. Km) Most countries of any other continent Home to The Sahara, the largest desert in the world and The Nile, the longest river in the world The Sahara: covers 4,619,260 km2 The Nile: 6695 kilometers long There are over 1000 languages spoken in Africa http://www.ecdc-cari.org/countries/Africa_Map.gif North America Third largest continent on earth (24,256,000 Sq. Km) Composed of 23 countries Most North Americans speak French, Spanish, and English Only continent that has every kind of climate http://www.freeusandworldmaps.com/html/WorldRegions/WorldRegions.html Asia Largest continent in size and population (44,579,000 Sq. Km) Contains 47 countries Contains the world’s largest country, Russia, and the most populous country, China The Great Wall of China is the only man made structure that can be seen from space Home to Mt. Everest (on the border of Tibet and Nepal), the highest point on earth Mt. Everest is 29,028 ft. (8,848 m) tall http://craigwsmall.wordpress.com/2008/11/10/asia/ Europe Second smallest continent in the world (9,938,000 Sq. Km) Home to the smallest country (Vatican City State) There are no deserts in Europe Contains mineral resources: coal, petroleum, natural gas, copper, lead, and tin http://www.knowledgerush.com/wiki_image/b/bf/Europe-large.png Oceania/Australia Smallest continent on earth (7,687,000 Sq. -

Implementing Eratosthenes' Discovery in the Classroom: Educational
Implementing Eratosthenes’ Discovery in the Classroom: Educational Difficulties Needing Attention Nicolas Decamp, C. de Hosson To cite this version: Nicolas Decamp, C. de Hosson. Implementing Eratosthenes’ Discovery in the Classroom: Educational Difficulties Needing Attention. Science and Education, Springer Verlag, 2012, 21 (6), pp.911-920. 10.1007/s11191-010-9286-3. hal-01663445 HAL Id: hal-01663445 https://hal.archives-ouvertes.fr/hal-01663445 Submitted on 18 Dec 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Sci & Educ DOI 10.1007/s11191-010-9286-3 Implementing Eratosthenes’ Discovery in the Classroom: Educational Difficulties Needing Attention Nicolas De´camp • Ce´cile de Hosson Ó Springer Science+Business Media B.V. 2010 Abstract This paper presents a critical analysis of the accepted educational use of the method performed by Eratosthenes to measure the circumference of Earth which is often considered as a relevant means of dealing with issues related to the nature of science and its history. This method relies on a number of assumptions among which the parallelism of sun rays. The assumption of sun rays parallelism (if it is accurate) does not appear spontaneous for students who consider sun rays to be divergent. -

Geography Notes.Pdf
THE GLOBE What is a globe? a small model of the Earth Parts of a globe: equator - the line on the globe halfway between the North Pole and the South Pole poles - the northern-most and southern-most points on the Earth 1. North Pole 2. South Pole hemispheres - half of the earth, divided by the equator (North & South) and the prime meridian (East and West) 1. Northern Hemisphere 2. Southern Hemisphere 3. Eastern Hemisphere 4. Western Hemisphere continents - the largest land areas on Earth 1. North America 2. South America 3. Europe 4. Asia 5. Africa 6. Australia 7. Antarctica oceans - the largest water areas on Earth 1. Atlantic Ocean 2. Pacific Ocean 3. Indian Ocean 4. Arctic Ocean 5. Antarctic Ocean WORLD MAP ** NOTE: Our textbooks call the “Southern Ocean” the “Antarctic Ocean” ** North America The three major countries of North America are: 1. Canada 2. United States 3. Mexico Where Do We Live? We live in the Western & Northern Hemispheres. We live on the continent of North America. The other 2 large countries on this continent are Canada and Mexico. The name of our country is the United States. There are 50 states in it, but when it first became a country, there were only 13 states. The name of our state is New York. Its capital city is Albany. GEOGRAPHY STUDY GUIDE You will need to know: VOCABULARY: equator globe hemisphere continent ocean compass WORLD MAP - be able to label 7 continents and 5 oceans 3 Large Countries of North America 1. United States 2. Canada 3. -

Was This World Map Made Ten Centuries Ago?
HAWAIIAN GAZETTE, FRIDAY, JANUARY n, 1907 SEMI-WEEKL- Y Was This World Map Made Ten Centuries Ago? gg "J" ISOME DETAILS OF GREAT Vf? rr9rv-vr- i 'vir)('JK.rr KXW XXXjtXXmXmKiXXXiXXX XvyXXXrXXX ffKftXr1 STORM Politically Inclined policemen nro not wanted by tho new Sheriff, who will MAUI, shortly Issue nn order to the effect that January i. The holiday sea- son 2 i I nlj employes of tho police department on Maul has not been a tlmo of quiet 5 j ft must chooso between their Jobs on tho enjoyment ns far as weather is 5 a force and their oITlces In any of tho concerned. Dame Nnturo has echoed A.- -. a. w three political party committees. This anything but the Christmas sentiment rule Is to bo strictly enforced, the em of "peace on earth and good-wi- lt ployes of tho public being supposed, bo mn." far as tho police are concernod at least, Before recovery could bo made from to give their time and energy to th tho effects of the recent north storm public and not for the advancement with Its 20 Inches of moisture In local- politically or otherwlso of any one sec- ities, on Saturday tho wind changed Ifr tion of tho public to the southucst and nn kona Tho Sheriff Is making plain storm came Into being. It contin- If It that ued to blow fiercely ho means ho says all tho night what when he tabued through, accompanied by nn Incessant i - i politics around tho police station. In piny of lightning and the heavy roll of this he has come In for moro or less thunder. -

Astronomy and Hipparchus
CHAPTER 9 Progress in the Sciences: Astronomy and Hipparchus Klaus Geus Introduction Geography in modern times is a term which covers several sub-disciplines like ecology, human geography, economic history, volcanology etc., which all con- cern themselves with “space” or “environment”. In ancient times, the definition of geography was much more limited. Geography aimed at the production of a map of the oikoumene, a geographer was basically a cartographer. The famous scientist Ptolemy defined geography in the first sentence of his Geographical handbook (Geog. 1.1.1) as “imitation through drafting of the entire known part of the earth, including the things which are, generally speaking, connected with it”. In contrast to chorography, geography uses purely “lines and label in order to show the positions of places and general configurations” (Geog. 1.1.5). Therefore, according to Ptolemy, a geographer needs a μέθοδος μαθεματική, abil- ity and competence in mathematical sciences, most prominently astronomy, in order to fulfil his task of drafting a map of the oikoumene. Given this close connection between geography and astronomy, it is not by default that nearly all ancient “geographers” (in the limited sense of the term) stood out also as astronomers and mathematicians: Among them Anaximander, Eudoxus, Eratosthenes, Hipparchus, Poseidonius and Ptolemy are the most illustrious. Apart from certain topics like latitudes, meridians, polar circles etc., ancient geography also took over from astronomy some methods like the determina- tion of the size of the earth or of celestial and terrestrial distances.1 The men- tioned geographers Anaximander, Eudoxus, Hipparchus, Poseidonius and Ptolemy even constructed instruments for measuring, observing and calculat- ing like the gnomon, sundials, skaphe, astrolabe or the meteoroscope.2 1 E.g., Ptolemy (Geog. -
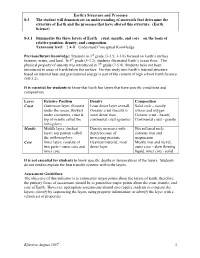
Earth's Structure and Processes 8-3 the Student Will Demonstrate An
Earth’s Structure and Processes 8-3 The student will demonstrate an understanding of materials that determine the structure of Earth and the processes that have altered this structure. (Earth Science) 8-3.1 Summarize the three layers of Earth – crust, mantle, and core – on the basis of relative position, density, and composition. Taxonomy level: 2.4-B Understand Conceptual Knowledge Previous/future knowledge: Students in 3rd grade (3-3.5, 3-3.6) focused on Earth’s surface features, water, and land. In 5th grade (5-3.2), students illustrated Earth’s ocean floor. The physical property of density was introduced in 7th grade (7-5.9). Students have not been introduced to areas of Earth below the surface. Further study into Earth’s internal structure based on internal heat and gravitational energy is part of the content of high school Earth Science (ES-3.2). It is essential for students to know that Earth has layers that have specific conditions and composition. Layer Relative Position Density Composition Crust Outermost layer; thinnest Least dense layer overall; Solid rock – mostly under the ocean, thickest Oceanic crust (basalt) is silicon and oxygen under continents; crust & more dense than Oceanic crust - basalt; top of mantle called the continental crust (granite) Continental crust - granite lithosphere Mantle Middle layer, thickest Density increases with Hot softened rock; layer; top portion called depth because of contains iron and the asthenosphere increasing pressure magnesium Core Inner layer; consists of Heaviest material; most Mostly iron and nickel; two parts – outer core and dense layer outer core – slow flowing inner core liquid, inner core - solid It is not essential for students to know specific depths or temperatures of the layers. -

World Map of Al-‘Umari #226.1
World Map of al-‘Umari #226.1 TITLE: The Mamunic World Map DATE: 1340 AUTHOR: Ahmad ibn Yahya ibn Fadlallah al-‘Umari DESCRIPTION: The geographic work Masalik al-aNar fi mainalik al-amsar [Ways of Perception Concerning the Most Populous [Civilized] Provinces] was written by Ahmad Ibn Fadlalldh al-Umari (died 1349), a distinguished administrator and author who was active in Cairo and Damascus under Mamluk rule. He claims that the map is a copy of the world map made for Caliph al-Ma’mun (reigned 813-833); also mentioned by al-Mas’udi (#212) earlier. The world map shown here is reproduced in this manuscript of the work of al- ‘Umari. The same manuscript also has maps of the first three climates. Although the climates are not divided into sections, the general impression is that the maps are derived from those of al-Idrisi (#219). However, from its appearance it seems to have been compiled from the text of the Kitab bast al-ard fi tuliha wa-al-‘ard [Exposition of the earth in length and breadth] by Ibn Sa‘id (#221). Al-‘Umari’s text does mention a map and gives a few examples of longitude and latitude, but on the whole they do not correspond with positions given on the map. Most of the Istanbul manuscripts of Ibn Fadlallah al-‘Umari’s work are undated. However, the earliest one to be dated is 1585, suggesting that this and most other copies were prepared for the libraries of the Ottoman sultans of that period. By that time the idea of a graticule was well known from European sources and could have been added to bring the map up to date. -

1.1 Eratosthenes Measures the Earth (Copyright: Bryan Dorner All Rights Reserved)
1.1 Eratosthenes Measures the Earth (Copyright: Bryan Dorner all rights reserved) How big is the Earth? The mathematician Eratosthenes (276-195 BCE) lived in the city of Alexandria in northern Egypt near the place where the Nile river empties into the Mediterranean. Eratosthenes was chief librarian at the Alexandria museum and one of the foremost scholars of the day - second only to Archimedes (who many consider one of the two or three best mathematicians ever to have lived). The city of Alexandria had been founded about one hundred years earlier by Alexander the Great whose conquests stretched from Egypt, through Syria, Babylonia, and Persia to northern India and central Asia. As the Greeks were also called Hellenes, the resulting empire was known as the Hellenistic empire and the following period in which Greek culture was dominant is called the Hellenistic age. The Hellenistic age saw a considerable exchange of culture between the conquering Greeks and the civilizations of the lands they controlled. It is from about this period that the predominantly geometric mathematics of the Greeks shows a computational aspect borrowed from the Babylonians. Some of the best mathematics we have inherited comes from just such a blend of contributions from diverse cultures. Eratosthenes is known for his simple but accurate measurement of the size of the earth. The imprint of Babylon (modern Iraq) as well as Greece can be seen in his method. He did not divide the arc of a circle into 360 parts as the Babylonians did, but into 60 equal parts. Still, the use of 60 reveals the influence of the Babylonian number system - the sexagesimal system - which was based on the number 60 in the same way ours is based on the number 10. -

Comparison of Spherical Cube Map Projections Used in Planet-Sized Terrain Rendering
FACTA UNIVERSITATIS (NIS)ˇ Ser. Math. Inform. Vol. 31, No 2 (2016), 259–297 COMPARISON OF SPHERICAL CUBE MAP PROJECTIONS USED IN PLANET-SIZED TERRAIN RENDERING Aleksandar M. Dimitrijevi´c, Martin Lambers and Dejan D. Ranˇci´c Abstract. A wide variety of projections from a planet surface to a two-dimensional map are known, and the correct choice of a particular projection for a given application area depends on many factors. In the computer graphics domain, in particular in the field of planet rendering systems, the importance of that choice has been neglected so far and inadequate criteria have been used to select a projection. In this paper, we derive evaluation criteria, based on texture distortion, suitable for this application domain, and apply them to a comprehensive list of spherical cube map projections to demonstrate their properties. Keywords: Map projection, spherical cube, distortion, texturing, graphics 1. Introduction Map projections have been used for centuries to represent the curved surface of the Earth with a two-dimensional map. A wide variety of map projections have been proposed, each with different properties. Of particular interest are scale variations and angular distortions introduced by map projections – since the spheroidal surface is not developable, a projection onto a plane cannot be both conformal (angle- preserving) and equal-area (constant-scale) at the same time. These two properties are usually analyzed using Tissot’s indicatrix. An overview of map projections and an introduction to Tissot’s indicatrix are given by Snyder [24]. In computer graphics, a map projection is a central part of systems that render planets or similar celestial bodies: the surface properties (photos, digital elevation models, radar imagery, thermal measurements, etc.) are stored in a map hierarchy in different resolutions. -

9 · the Growth of an Empirical Cartography in Hellenistic Greece
9 · The Growth of an Empirical Cartography in Hellenistic Greece PREPARED BY THE EDITORS FROM MATERIALS SUPPLIED BY GERMAINE AUJAe There is no complete break between the development of That such a change should occur is due both to po cartography in classical and in Hellenistic Greece. In litical and military factors and to cultural developments contrast to many periods in the ancient and medieval within Greek society as a whole. With respect to the world, we are able to reconstruct throughout the Greek latter, we can see how Greek cartography started to be period-and indeed into the Roman-a continuum in influenced by a new infrastructure for learning that had cartographic thought and practice. Certainly the a profound effect on the growth of formalized know achievements of the third century B.C. in Alexandria had ledge in general. Of particular importance for the history been prepared for and made possible by the scientific of the map was the growth of Alexandria as a major progress of the fourth century. Eudoxus, as we have seen, center of learning, far surpassing in this respect the had already formulated the geocentric hypothesis in Macedonian court at Pella. It was at Alexandria that mathematical models; and he had also translated his Euclid's famous school of geometry flourished in the concepts into celestial globes that may be regarded as reign of Ptolemy II Philadelphus (285-246 B.C.). And it anticipating the sphairopoiia. 1 By the beginning of the was at Alexandria that this Ptolemy, son of Ptolemy I Hellenistic period there had been developed not only the Soter, a companion of Alexander, had founded the li various celestial globes, but also systems of concentric brary, soon to become famous throughout the Mediter spheres, together with maps of the inhabited world that ranean world. -

10 · Greek Cartography in the Early Roman World
10 · Greek Cartography in the Early Roman World PREPARED BY THE EDITORS FROM MATERIALS SUPPLIED BY GERMAINE AUJAe The Roman republic offers a good case for continuing to treat the Greek contribution to mapping as a separate CONTINUITY AND CHANGE IN THEORETICAL strand in the history ofclassical cartography. While there CARTOGRAPHY: POLYBIUS, CRATES, was a considerable blending-and interdependence-of AND HIPPARCHUS Greek and Roman concepts and skills, the fundamental distinction between the often theoretical nature of the Greek contribution and the increasingly practical uses The extent to which a new generation of scholars in the for maps devised by the Romans forms a familiar but second century B.C. was familiar with the texts, maps, satisfactory division for their respective cartographic in and globes of the Hellenistic period is a clear pointer to fluences. Certainly the political expansion of Rome, an uninterrupted continuity of cartographic knowledge. whose domination was rapidly extending over the Med Such knowledge, relating to both terrestrial and celestial iterranean, did not lead to an eclipse of Greek influence. mapping, had been transmitted through a succession of It is true that after the death of Ptolemy III Euergetes in well-defined master-pupil relationships, and the pres 221 B.C. a decline in the cultural supremacy of Alex ervation of texts and three-dimensional models had been andria set in. Intellectual life moved to more energetic aided by the growth of libraries. Yet this evidence should centers such as Pergamum, Rhodes, and above all Rome, not be interpreted to suggest that the Greek contribution but this promoted the diffusion and development of to cartography in the early Roman world was merely a Greek knowledge about maps rather than its extinction.