"Containment Internal Pressure Capacity,DC Cook Nuclear
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Channel Lineup
Break free from traditional TV! Channel Lineup | 1 A TV experience that's all about you. Whether you’re a sports fan, news enthusiast or all-around entertainment junkie, there’s something for you. Choose from one of our pre-assembled Value packages or build your own lineup with our Micro package. Add theme packs, premium channels and a variety of individual channels to personalize your TV. base packages All packages give you access to: ✓ One AccessNexTV set-top box included ✓ AccessNow TV community channel ✓ 24/7 customer service ✓ Streaming Go Apps ✓ On demand ✓ No contracts Value Packages - We've made it easy for you by grouping our most popular channels. The easiest way to select your programming, offering the best value on our most popular channels grouped and ready for you. Enhance your entertainment with movies, premium sports, specialty channels, theme packs and more. Bronze HD –$59.95/mth. For the lite TV viewer. Includes major networks and some news, sports and kids programming. Silver HD – $72.95/mth. For the moderate TV viewer. All the channels in Bronze HD are included, along with more sports, family and entertainment including Sportsnet and the US Superstations. Gold HD – $86.95/mth. For the mighty TV viewer. All the channels in Silver HD are included plus our most popular mix of entertainment, news, sports and family channels. OR Micro Package - Know what you want? Customize your own TV experience. Micro is our lowest priced, base package and the perfect foundation for your own personalized TV experience. Key channels including Canadian and U.S. -

Channel Listing Satellite Tv Current As of February 11, 2021
CHANNEL LISTING SATELLITE TV CURRENT AS OF FEBRUARY 11, 2021. CLASSICAL 96FM TORONTO ...............963 N STINGRAY LOUD .........................................580 GOOD CLUB JUNIOR......................... (ON DEMAND) NEWSTALK 1010 ...........................................964 STINGRAY MUSIC STATIONS .......901-947 COUNTRY FM 105 .......................................968 NPR (NATIONAL PUBLIC RADIO) ........965 STINGRAY RETRO ........................................578 THE MAJOR NETWORKS, PLUS A SELECTION CTV - KINGSTON (CKWS) .......................233 O STINGRAY VIBE .............................................579 OF SPECIALTY CHANNELS. INCLUDES ALL OF CTV - OSHAWA (CHEX2).........................583 OZ-FM - ST. JOHN’S ....................................951 T THE CHANNELS IN THE STARTER PACKAGE. CTV - PETERBOROUGH (CHEX) ............217 P THE WEATHER NETWORK ......................505 # F PALMARÈSADISQ PAR STINGRAY .......187 TSC ......................................................................660 * 102.1 THE EDGE ............................................. 955 FAITHTV ...........................................................591 PLANETE JAZZ .............................................960 TSN RADIO 1050 ......................................... 995 104.5 CHUM FM ...........................................990 I PREMIÈRE CHAÎNE FM 97.7 TSN RADIO 1290 WINNIPEG ................. 984 680 NEWS ...................................................... 958 ICI MUSIQUE - MONTREAL (CBFX FM) .975 VANCOUVER (CBUF-FM) .........................977 -

Download the Complete Satellite TV Channel List
CHANNEL LISTING SATELLITE TV CURRENT AS OF JULY 5, 2021. CTV DRAMA CHANNEL ...........................620 NOOVO - MONTRÉAL HD* .................. 1803 TLN ......................................................................700 GOOD CTV DRAMA CHANNEL HD ..................1734 NOOVO - QUÉBEC* ....................................109 THE NEWS FORUM .....................................506 CTV NEWS CHANNEL................................501 NOOVO - SAGUENAY* ..............................104 THE WEATHER NETWORK ......................505 THE MAJOR NETWORKS, PLUS A SELECTION CTV NEWS CHANNEL HD .....................1562 NOOVO - SHERBROOKE* .......................106 TOON-A-VISION ..........................................567 OF SPECIALTY CHANNELS. INCLUDES ALL OF CTV SCI-FI CHANNEL ...............................627 NOOVO - TROIS-RIVIERES* .................540 TREEHOUSE ................................................... 553 THE CHANNELS IN THE STARTER PACKAGE. CTV SCI-FI CHANNEL HD ..................... 1746 NOOVO - VAL-D’OR* ................................ 544 TREEHOUSE HD .........................................1640 NPR (NATIONAL PUBLIC RADIO) ........965 TSC ......................................................................660 # D NTV ...................................................................... 199 TSN1 ....................................................................400 102.1 THE EDGE ............................................. 955 DAYSTAR CANADA .....................................650 NTV HD ...........................................................1008 -

GRILLE DE CHAÎNES NATIONALE (ORDRE NUMÉRIQUE) Octobre 2020
GRILLE DE CHAÎNES NATIONALE (ORDRE NUMÉRIQUE) Octobre 2020 100 Chaînes Atlantique HD 164 Citytv Winnipeg HD 238 CBS West HD 327 ESPN Classic 101 Global Halifax HD 170 Chaînes Saskatchewan HD 239 Fox West HD 328 Sportsnet World HD 102 CBC Halifax HD 171 Global Regina HD 240 NBC West HD 329 beIN SPORTS HD 103 CTV Halifax HD 172 CBC Regina HD 241 PBS Seattle HD 330 WWE Network HD 104 CTV2 Atlantic HD 173 CTV Regina HD 242 PBS Spokane HD 331 Leafs TV HD 105 Global New Brunswick HD 174 Citytv Saskatchewan HD 243 myTV38 HD (WSBK Boston) 336 Fox Sports Racing HD 106 CBC Frederiction HD 175 Global Saskatoon HD 244 PIX 11 HD (The CW New York) 337 Cowboy Channel Canada HD 107 CTV Saint John HD 176 CTV Saskatoon HD 245 WGN Chicago HD 338 The Water Channel HD 108 CTV Moncton HD 177 CTV Prince Albert HD 246 KTLA 5 CW Los Angeles HD 350 Chaînes pour enfants HD 109 CBC Charlottetown HD 178 CTV Yorkton HD 252 The Weather Network HD 351 Treehouse HD 110 CTV Sydney HD 179 CKSA Lloydminster HD 253 aptn HD 352 Disney Junior HD 111 CBC Newfoundland HD 180 CITL Lloydminster HD 254 CPAC HD 353 Family Jr. HD 112 NTV Newfoundland HD 181 Northern Legislative Assembly 255 CBC News Network HD 361 Nickelodeon HD 120 Chaînes Québec HD (anglais) 182 OMNI Prairies HD 256 CTV News Channel HD 362 YTV HD 121 Global Montreal HD 190 Chaînes Alberta HD 257 BNN Bloomberg HD 363 YTV West HD 122 CBC Montreal HD 191 Global Edmonton HD 258 CNN HD 364 Disney XD HD 123 CTV Montreal HD 192 CBC Edmonton HD 259 HLN HD 365 CHRGD HD 124 Citytv Montreal HD 193 CTV Edmonton HD 260 MSNBC -

Organigramme De Propriété 143N
BCE Bell Média Radio & Télé #143n Propriété – Radiodiffusion - CRTC 2021-01-15 MISE À JOUR CRTC 2018-57 – a approuvé l’acquisition par Bell Média inc. des actifs de CICZ-FM Midland, CICX-FM Orillia, CJOS-FM Owen Sound et CICS-FM Sudbury de Larche Communications Inc. CRTC 2019-14 – a apprové une réorganisation intrasociété en plusieurs étapes par: 1. L’acquisition par une nouvelle société par actions de l’actif des services exploités actuellement par Bell Media Radio (Toronto) Inc. et 4382072 Canada Inc., associés dans une société en nom collectif faisant affaire sous le nom de Bell Média Radio s.e.n.c. À la suite d’une fusion, Bell Média inc. deviendra titulaire de ces entreprises. 2. Bell Média et 8384819 Canada Inc. deviendront associés d’une nouvelle société en nom collectif qui remplacera les sociétés en nom collectif faisant actuellement affaire sous les noms de Bell Media Windsor Radio Partnership, Bell Media Ontario Regional Radio Partnership, Bell Media Ottawa Radio Partnership, Bell Media Toronto Radio 2013 Partnership, Bell Media Canada Radio 2013 Partnership et Bell Media British Columbia Radio Partnership. CRTC 2020-116 & CRTC 2020-154 – fusion de Groupe V Média inc. et sa fiiliale V Interactions inc. pour former une société dont le nom reste à déterminer (VFusion). Après la fusion, toutes les actions émises et en circulation de VFusion seront transférées de Remstar et autres actionnaires à Bell Canada. Par la suite, les actions de VFusion seront transférées à Bell Média inc. NOTE : Les changements de propriétés ont été reflétés. Mise à jour – 2020-04-14 – constitution de 11749366 Canada Inc. -

Santa Time: ,743915 Received by 27071 Members From
V EDISONf FORDS BRACON Woodbrirlge, A^nel, Colonia, Fordi, HopehnJts*ef in, Keasbey, Port Reading, Sewm-cn rod LV — No. 30 intend M »<> Olaa tfell PEgCETKN CENTS Woodbridge, N. J., Thursday, November 14, 1963 in H. 1. On Thundtj At P.O.O , wawd (i i WOODBRIDGE - Today, UM 18th ewaecntWe Independent- Each family receives a Christmas basket filled with every- Leader Chrlitmas Fund, to take care of the Tnwiuhtp'n nerdy thing necessary for a Christmas dinner including turkey, pars- at ChrhtUM. officially open*. ley, cettry, bread, butter, potatoes, sweet potatoes, cranberry Starting with less than 20 families 18 years ago, the Fund sauce, pickles, lettuce, tomatoes, mayonnaise, peas, onions, Santa Time: now takes core of over 100 needy families — some famille* small white onions, turnips, carrots, apples, oranges, canned with as many as 10 children in them, fruit salad, r^ard candy, tea, coffee, canned milk, fresh milk Public May Be The Independent-Leader started off the 1KB Fnd wKh Hi and sugar. usual contribution of *50 aad the reader who In again the flnt Under no circumstances will the name o( a family be re- contributor l> William S. Neebe, 417 Ehnwood Arenne, Wood- vealed. Back family will be given a number and will be iden- bridge, who i«nt $15. L tified by that number. Persons or organliatlons donating $2J w Independent-Leader Last year, we established the policy for the first time of or more may have a can) inserted indicating they are the not accepting used clothing or used toys because some of the donor. -
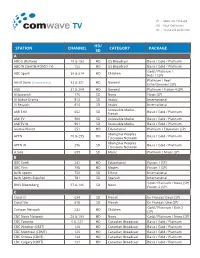
Comwavetv Channel Guide
SP - Specialty Package HD - High Definition SD - Standard Definition HD/ STATION CHANNEL CATEGORY PACKAGE SD A ABC-E (Buffalo) 18 & 153 HD US Broadcast Basic / Gold / Platinum ABC-W (Seattle-KOMO-TV) 155 HD US Broadcast Basic / Gold / Platinum Gold / Platinum / ABC Spark 58 & 214 HD Children Kids 1 (SP) Platinum / Reel Adult Swim (formerly Action) 82 & 321 HD General Entertainment (SP) A&E 31 & 284 HD General Platinum / Fusion 4 (SP) Al Jezeerah 176 SD News News (SP) Al Nahar Drama 813 SD Arabic International Al Resalah 814 SD Arabic International Accessible Media - AMI Télé 652 SD Basic / Gold / Platinum French AMI TV 900 SD Accessible Media Basic / Gold / Platinum AMI TV W 901 SD Accessible Media Basic / Gold / Platinum Animal Planet 251 HD Educational Platinum / Education (SP) Aboriginal Peoples APTN 70 & 295 HD Basic / Gold / Platinum Television Network Aboriginal Peoples APTN W 296 SD Basic / Gold / Platinum Television Network A.Side 699 SD Music Platinum / Music (SP) B BBC Earth 241 HD Educational Fusion 1 (SP) BBC First 708 HD Movies Fusion 1 (SP) beIN Sports 750 SD Ethnic International beIN Sports Español 781 SD Spanish International Gold / Platinum / News (SP) BNN Bloomberg 57 & 186 SD News Fusion 2 (SP) C Canal D 634 SD French En Français Deux (SP) Canal Vie 618 SD French En Français Une (SP) Gold / Platinum / Kids 2 Cartoon Network 232 HD Children (SP) CBC News Network 26 & 189 HD News Gold / Platinum / News (SP) CBC Toronto 6 & 127 HD Canadian Broadcast Basic / Gold / Platinum CBC Windsor (CBET) 126 HD Canadian Broadcast Basic -

BCE 2020 Annual Report
IN TWENTY-TWENTY WE WERE AT THE OF CONNECTIONS WHEN IT MATTERED MOST. ANNUAL REPORT 2020 Advancing how Canadians connect with each other and the world OUR FINANCIAL PERFORMANCE Stepping up in a year like no other As the Bell team kept Canada connected in a challenging 2020, we built marketplace momentum with world-class network, service and content innovations for our customers while delivering sustainable dividend growth for our shareholders. 2020 financial performance Revenue * (3.8%) Adjusted EBITDA (1) * (4.0%) Capital intensity 18.4% Adjusted EPS (1) $3.02 Free cash flow (1) * (10.4%) * Compared to 2019 6.1 % +307% Dividend yield Total shareholder in 2020 (2) return 2009–2020 (3) +5.1 % +140% Increase in dividend Increase in dividend per common share per common share for 2021 2009–2021 (1) Adjusted EBITDA, adjusted EPS and free cash floware non-GAAP financial measures and do not have any standardized meaning under International Financial Reporting Standards (IFRS). Therefore, they are unlikely to be comparable to similar measures presented by other issuers. For a full description of these measures, see section 10.2, Non-GAAP financial measures and key performance indicators (KPIs) on pp. 115 to 117 of the MD&A. (2) Annualized dividend per BCE common share divided by BCE’s share price at the end of the year. (3) The change in BCE’s common share price for a specified period plus BCE common share dividends reinvested, divided by BCE’s common share price at the beginning of the period. 2 | BCE INC. 2020 AnnuAL REPORT OUR PURPOSE Bell’s goal and Strategic Imperatives Our goal is to advance how Canadians connect with each other and the world, and the Bell team is executing a clear strategy that leverages our strengths and highlights the opportunities of the broadband economy for our company and all our stakeholders. -

USCIS - H-1B Approved Petitioners Fis…
5/4/2010 USCIS - H-1B Approved Petitioners Fis… H-1B Approved Petitioners Fiscal Year 2009 The file below is a list of petitioners who received an approval in fiscal year 2009 (October 1, 2008 through September 30, 2009) of Form I-129, Petition for a Nonimmigrant Worker, requesting initial H- 1B status for the beneficiary, regardless of when the petition was filed with USCIS. Please note that approximately 3,000 initial H- 1B petitions are not accounted for on this list due to missing petitioner tax ID numbers. Related Files H-1B Approved Petitioners FY 2009 (1KB CSV) Last updated:01/22/2010 AILA InfoNet Doc. No. 10042060. (Posted 04/20/10) uscis.gov/…/menuitem.5af9bb95919f3… 1/1 5/4/2010 http://www.uscis.gov/USCIS/Resource… NUMBER OF H-1B PETITIONS APPROVED BY USCIS IN FY 2009 FOR INITIAL BENEFICIARIES, EMPLOYER,INITIAL BENEFICIARIES WIPRO LIMITED,"1,964" MICROSOFT CORP,"1,318" INTEL CORP,723 IBM INDIA PRIVATE LIMITED,695 PATNI AMERICAS INC,609 LARSEN & TOUBRO INFOTECH LIMITED,602 ERNST & YOUNG LLP,481 INFOSYS TECHNOLOGIES LIMITED,440 UST GLOBAL INC,344 DELOITTE CONSULTING LLP,328 QUALCOMM INCORPORATED,320 CISCO SYSTEMS INC,308 ACCENTURE TECHNOLOGY SOLUTIONS,287 KPMG LLP,287 ORACLE USA INC,272 POLARIS SOFTWARE LAB INDIA LTD,254 RITE AID CORPORATION,240 GOLDMAN SACHS & CO,236 DELOITTE & TOUCHE LLP,235 COGNIZANT TECH SOLUTIONS US CORP,233 MPHASIS CORPORATION,229 SATYAM COMPUTER SERVICES LIMITED,219 BLOOMBERG,217 MOTOROLA INC,213 GOOGLE INC,211 BALTIMORE CITY PUBLIC SCH SYSTEM,187 UNIVERSITY OF MARYLAND,185 UNIV OF MICHIGAN,183 YAHOO INC,183 -

Q2 2021 Press Release
This news release contains forward-looking statements. For a description of the related risk factors and assumptions, please see the section entitled “Caution Regarding Forward-Looking Statements” later in this news release. BCE reports second quarter 2021 results • Net earnings increased 149.7% to $734 million with net earnings attributable to common shareholders growing 189% to $685 million, or $0.76 per common share, up 192.3%; 31.1% higher adjusted net earnings(1) of $751 million generated adjusted EPS(1) of $0.83, up 31.7% • Delivered 6.4% consolidated revenue growth and 6.2% higher adjusted EBITDA(2) • 115,916 total wireless mobile phone and mobile connected device, retail Internet and IPTV net additions, up 75% year over year • Leading growth in wireless service revenue and mobile phone average billing per user (ABPU) (4) as we welcomed 44,433 postpaid mobile phone net additions, up by 45,393, and increased net mobile connected device additions 22.2% to 47,449 • Retail Internet fibre net additions up 80% to 27,112, with 12% residential Internet revenue growth; up to 900,000 new fibre and WHI locations to be passed in 2021 • Growing 5G leadership: Total 3.5 GHz mobile spectrum holdings of 1,690M MHz-POP; strategic cloud and technology partnerships with AWS and Google Cloud; on track to cover 70% of national population with 5G service by year end • Strong financial position including $5.3 billion of available liquidity(5) enabling accelerated capital investment, wireless spectrum purchases and dividend growth • Ongoing industry leadership in ESG standards highlighted by the launch of the Bell for Better initiative MONTRÉAL, August 5, 2021 – BCE Inc. -

Selected Thermodynamic Properties for Mixtures of R-32
NIATX INST. OF STAND & TECH R.I.C. NISI PUBLICATIONS AlllDS 3SS3S3 United States Department of Commerce Technology Administration fMisr National Institute of Standards and Technology NIST Technical Note 1397 Selected Thermodynamic Properties for IVIixtures of R-32 (Difluoromethane), R-125 (Pentafluoroethane), R-134A (1 ,1 ,1 ,2-Tetrafluoroethane), R-143A (1,1,1-Trifluoroethane), R-41 (Fluorometliane), R-290 (Propane), and R-744 (Carbon Dioxide) Cynthia D. Holcomb Joseph W. Magee Jennifer L. Scott Stephanie L. Outcalt William M. Haynes QC 100 U5753 NO. 1397 1997 NIST Technical Note 1397 Selected Thermodynamic Properties for Mixtures of R-32 (Difluoromethane), R-125 (Pentafluoroethane), R-134A (1 ,1,1 ,2-Tetrafluoroethane), R-143A (1,1J-Trifluoroethane), R-41 (Fluoromethane), R-290 (Propane), and R-744 (Carbon Dioxide) Cynthia D. Holcomb Joseph W. Magee Jennifer L. Scott Stephanie L. Outcalt William M. Haynes Physical and Chemical Properties Division Chemical Science and Technology Laboratory National Institute of Standards and Technology 325 Broadway Boulder, Colorado 80303-3328 December 1997 f/ \ ''^ATSS O* U.S. DEPARTMENT OF COMMERCE, William M. Daley, Secretary TECHNOLOGY ADMINISTRATION, Gcry R. Bachula, Acting Under Secretary for Technology NATIONAL INSTITUTE OF STANDARDS AND TECHNOLOGY, Raymond G. Kammer, Director National Institute of Standards and Technology Technical Note Natl. Inst. Stand. Technol., Tech. Note 1397, 200 pages (December 1997) CODEN:NTNOEF U.S. GOVERNMENT PRINTING OFFICE WASHINGTON: 1997 For sale by the Superintendent of Documents, U.S. Government Printing Office, Washington, DC 20402-9325 1 TABLE OF CONTENTS Page LIST OF FIGURES iv LIST OF TABLES vii L INTRODUCTION 1 2. SIGNIRCANT RESULTS 2 2.1 Thermophysical Properties of R-32/125/134a and Its Constituent Binaries 2 2.1.1 R-32/134a 3 2.1.2 R-32/125 4 2.1.3 R-125/134a 5 2.1.4 R-32/125/134a 5 2.2 Mixtures withR-143a 6 2.2.1 R-32/143a 6 2.2.2 R-125/143a 7 2.2.3 R-143a/134a 8 2.3 Mixtures with R-290 8 2.3.1 R-32/290 '. -

Canada’S Communications Magazine
www.broadcastermagazine.com November 2016 $8.00 CANADA’S COMMUNICATIONS MAGAZINE FALL BUYERS’ GUIDE We curate. You create. The Canada Media Fund publishes CMF Trends, a curated source of information that helps you better understand the ongoing changes happening in the world of media and technology. Discover more at CMF-FMC.CA - f in Brought to you by the Government of Canada and Canada's cable, satellite and IPTV distributors. EYE Canada Media Fund C) ON TRENDS CANADA Fonds des medias du Canada Job # CMF_16088 Filename CMF_16088_Broadcaster_Fall Directory_FP_OL.indd Modified 10-27-2016 11:58 AM Created 10-27-2016 11:54 AM Station Micheline Carone Client Contact None Publication(s) Broadcaster Fall Directory CMYK Helvetica Neue LT Std Art Director Mo Ad Number None Production None PUBLICATION Insertion Date None Copy Writer None Bleed 8.375” x 11” INKS INKS PERSONNEL Production Artist Mich Trim 8.125” x 10.75” SETUP Comments full page ad (8.125” x 10.75”) Safety 7” x 10” Editor Lee Rickwood [email protected] Senior Publisher Advertising Sales James A. Cook (416) 510-6871 [email protected] Broadcaster® November 2016 Volume 75 Number 3 Print Production Manager Phyllis Wright (416) 510-6786 Production Manager Alicia Lerma 416-442-5600, Ext 3588 [email protected] Circulation Manager Barbara Adelt 416-442-5600, Ext. 3546 [email protected] Customer Service Bona Lao 416-442-5600, Ext 3552 [email protected] News Service Broadcast News Limited Editorial Deadline Five weeks before publication date. Broadcaster® is published 9 times yearly, by Annex Newcom LP Head Office 80 Valleybrook Drive, 2017 FALL Toronto, Ontario M3B 2S9 Fax: (416) 510-5140 Indexed in Canada Business Index BUYERS’ GUIDE Print edition: ISSN 0008-3038 Online edition: ISSN 1923-340X Iii Miance for .