Basic Compiler Algorithms for Parallel Programs *
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

About ILE C/C++ Compiler Reference
IBM i 7.3 Programming IBM Rational Development Studio for i ILE C/C++ Compiler Reference IBM SC09-4816-07 Note Before using this information and the product it supports, read the information in “Notices” on page 121. This edition applies to IBM® Rational® Development Studio for i (product number 5770-WDS) and to all subsequent releases and modifications until otherwise indicated in new editions. This version does not run on all reduced instruction set computer (RISC) models nor does it run on CISC models. This document may contain references to Licensed Internal Code. Licensed Internal Code is Machine Code and is licensed to you under the terms of the IBM License Agreement for Machine Code. © Copyright International Business Machines Corporation 1993, 2015. US Government Users Restricted Rights – Use, duplication or disclosure restricted by GSA ADP Schedule Contract with IBM Corp. Contents ILE C/C++ Compiler Reference............................................................................... 1 What is new for IBM i 7.3.............................................................................................................................3 PDF file for ILE C/C++ Compiler Reference.................................................................................................5 About ILE C/C++ Compiler Reference......................................................................................................... 7 Prerequisite and Related Information.................................................................................................. -

Compiler Error Messages Considered Unhelpful: the Landscape of Text-Based Programming Error Message Research
Working Group Report ITiCSE-WGR ’19, July 15–17, 2019, Aberdeen, Scotland Uk Compiler Error Messages Considered Unhelpful: The Landscape of Text-Based Programming Error Message Research Brett A. Becker∗ Paul Denny∗ Raymond Pettit∗ University College Dublin University of Auckland University of Virginia Dublin, Ireland Auckland, New Zealand Charlottesville, Virginia, USA [email protected] [email protected] [email protected] Durell Bouchard Dennis J. Bouvier Brian Harrington Roanoke College Southern Illinois University Edwardsville University of Toronto Scarborough Roanoke, Virgina, USA Edwardsville, Illinois, USA Scarborough, Ontario, Canada [email protected] [email protected] [email protected] Amir Kamil Amey Karkare Chris McDonald University of Michigan Indian Institute of Technology Kanpur University of Western Australia Ann Arbor, Michigan, USA Kanpur, India Perth, Australia [email protected] [email protected] [email protected] Peter-Michael Osera Janice L. Pearce James Prather Grinnell College Berea College Abilene Christian University Grinnell, Iowa, USA Berea, Kentucky, USA Abilene, Texas, USA [email protected] [email protected] [email protected] ABSTRACT of evidence supporting each one (historical, anecdotal, and empiri- Diagnostic messages generated by compilers and interpreters such cal). This work can serve as a starting point for those who wish to as syntax error messages have been researched for over half of a conduct research on compiler error messages, runtime errors, and century. Unfortunately, these messages which include error, warn- warnings. We also make the bibtex file of our 300+ reference corpus ing, and run-time messages, present substantial difficulty and could publicly available. -

ROSE Tutorial: a Tool for Building Source-To-Source Translators Draft Tutorial (Version 0.9.11.115)
ROSE Tutorial: A Tool for Building Source-to-Source Translators Draft Tutorial (version 0.9.11.115) Daniel Quinlan, Markus Schordan, Richard Vuduc, Qing Yi Thomas Panas, Chunhua Liao, and Jeremiah J. Willcock Lawrence Livermore National Laboratory Livermore, CA 94550 925-423-2668 (office) 925-422-6278 (fax) fdquinlan,panas2,[email protected] [email protected] [email protected] [email protected] [email protected] Project Web Page: www.rosecompiler.org UCRL Number for ROSE User Manual: UCRL-SM-210137-DRAFT UCRL Number for ROSE Tutorial: UCRL-SM-210032-DRAFT UCRL Number for ROSE Source Code: UCRL-CODE-155962 ROSE User Manual (pdf) ROSE Tutorial (pdf) ROSE HTML Reference (html only) September 12, 2019 ii September 12, 2019 Contents 1 Introduction 1 1.1 What is ROSE.....................................1 1.2 Why you should be interested in ROSE.......................2 1.3 Problems that ROSE can address...........................2 1.4 Examples in this ROSE Tutorial...........................3 1.5 ROSE Documentation and Where To Find It.................... 10 1.6 Using the Tutorial................................... 11 1.7 Required Makefile for Tutorial Examples....................... 11 I Working with the ROSE AST 13 2 Identity Translator 15 3 Simple AST Graph Generator 19 4 AST Whole Graph Generator 23 5 Advanced AST Graph Generation 29 6 AST PDF Generator 31 7 Introduction to AST Traversals 35 7.1 Input For Example Traversals............................. 35 7.2 Traversals of the AST Structure............................ 36 7.2.1 Classic Object-Oriented Visitor Pattern for the AST............ 37 7.2.2 Simple Traversal (no attributes)....................... 37 7.2.3 Simple Pre- and Postorder Traversal.................... -

A Compiler-Compiler for DSL Embedding
A Compiler-Compiler for DSL Embedding Amir Shaikhha Vojin Jovanovic Christoph Koch EPFL, Switzerland Oracle Labs EPFL, Switzerland {amir.shaikhha}@epfl.ch {vojin.jovanovic}@oracle.com {christoph.koch}@epfl.ch Abstract (EDSLs) [14] in the Scala programming language. DSL devel- In this paper, we present a framework to generate compil- opers define a DSL as a normal library in Scala. This plain ers for embedded domain-specific languages (EDSLs). This Scala implementation can be used for debugging purposes framework provides facilities to automatically generate the without worrying about the performance aspects (handled boilerplate code required for building DSL compilers on top separately by the DSL compiler). of extensible optimizing compilers. We evaluate the practi- Alchemy provides a customizable set of annotations for cality of our framework by demonstrating several use-cases encoding the domain knowledge in the optimizing compila- successfully built with it. tion frameworks. A DSL developer annotates the DSL library, from which Alchemy generates a DSL compiler that is built CCS Concepts • Software and its engineering → Soft- on top of an extensible optimizing compiler. As opposed to ware performance; Compilers; the existing compiler-compilers and language workbenches, Alchemy does not need a new meta-language for defining Keywords Domain-Specific Languages, Compiler-Compiler, a DSL; instead, Alchemy uses the reflection capabilities of Language Embedding Scala to treat the plain Scala code of the DSL library as the language specification. 1 Introduction A compiler expert can customize the behavior of the pre- Everything that happens once can never happen defined set of annotations based on the features provided by again. -

Wind River Diab Compiler
WIND RIVER DIAB COMPILER Boost application performance, reduce memory footprint, and produce high-quality, standards-compliant object code for embedded systems with Wind River® Diab Compiler. Wind River has a long history of providing software and tools for safety-critical applications requiring certification in the automotive, medical, avionics, and industrial markets. And it’s backed by an award-winning global support organization that draws on more than 25 years of compiler experience and hundreds of millions of successfully deployed devices. TOOLCHAIN COMPONENTS Diab Compiler includes the following programs and utilities: • Driver: Intelligent wrapper program invoking the compiler, assembler, and linker, using a single application • Assembler: Macro assembler invoked automatically by the driver program or as a complete standalone assembler generating object modules – Conditional macro assembler with more than 30 directives – Unlimited number of symbols – Debug information for source-level debugging of assembly programs • Compiler: ANSI/ISO C/C++ compatible cross-compiler – EDG front end – Support for ANSI C89, C99, and C++ 2003 – Hundreds of customizable optimizations for performance and size – Processor architecture–specific optimizations – Whole-program optimization capability • Low-level virtual machine (LLVM)–based technology: Member of the LLVM commu- nity, accelerating inclusion of new innovative compiler features and leveraging the LLVM framework to allow easy inclusion of compiler add-ons to benefit customers • Linker: Precise -

Compilers History Wikipedia History Main Article: History of Compiler
Compilers History Wikipedia History Main article: History of compiler construction Software for early computers was primarily written in assembly language for many years. Higher level programming languages were not invented until the benefits of being able to reuse software on different kinds of CPUs started to become significantly greater than the cost of writing a compiler. The very limited memory capacity of early computers also created many technical problems when implementing a compiler. Towards the end of the 1950s, machine-independent programming languages were first proposed. Subsequently, several experimental compilers were developed. The first compiler was written by Grace Hopper, in 1952, for the A-0 programming language. The FORTRAN team led by John Backus at IBM is generally credited as having introduced the first complete compiler in 1957. COBOL was an early language to be compiled on multiple architectures, in 1960. In many application domains the idea of using a higher level language quickly caught on. Because of the expanding functionality supported by newer programming languages and the increasing complexity of computer architectures, compilers have become more and more complex. Early compilers were written in assembly language. The first self-hosting compiler — capable of compiling its own source code in a high-level language — was created for Lisp by Tim Hart and Mike Levin at MIT in 1962. Since the 1970s it has become common practice to implement a compiler in the language it compiles, although both Pascal and C have been popular choices for implementation language. Building a self-hosting compiler is a bootstrapping problem—the first such compiler for a language must be compiled either by hand or by a compiler written in a different language, or (as in Hart and Levin's Lisp compiler) compiled by running the compiler in an interpreter. -

Compilers and Compiler Generators
Compilers and Compiler Generators an introduction with C++ © P.D. Terry, Rhodes University, 1996 [email protected] This is a set of Postcript® files of the text of my book "Compilers and Compiler Generators - an introduction with C++", published in 1997 by International Thomson Computer Press. The original edition is now out of print, and the copyright has reverted to me. The book is also available in other formats. The latest versions of the distribution and details of how to download up-to-date compressed versions of the text and its supporting software and courseware can be found at http://www.scifac.ru.ac.za/compilers/ The text of the book is Copyright © PD Terry. Although you are free to make use of the material for academic purposes, the material may not be redistributed without my knowledge or permission. File List The 18 chapters of the book are filed as chap01.ps through chap18.ps The 4 appendices to the book are filed as appa.ps through appd.ps The original appendix A of the book is filed as appa0.ps The contents of the book is filed as contents.ps The preface of the book is filed as preface.ps An index for the book is filed as index.ps. Currently (January 2000) the page numbers refer to an A4 version in PCL® format available at http://www.scifac.ru.ac.za/compilers/longpcl.zip. However, software tools like GhostView may be used to search the files for specific text. The bibliography for the book is filed as biblio.ps Change List 18-October-1999 - Pre-release 12-November-1999 - First official on-line release 16-January-2000 - First release of Postscript version (incorporates minor corrections to chapter 12) Compilers and Compiler Generators © P.D. -

Perl
-I<directory> directories specified by –I are Perl prepended to @INC -I<oct_name> enable automatic line-end processing Ming- Hwa Wang, Ph.D. -(m|M)[- executes use <module> before COEN 388 Principles of Computer- Aided Engineering Design ]<module>[=arg{,arg}] executing your script Department of Computer Engineering -n causes Perl to assume a loop around Santa Clara University -p your script -P causes your script through the C Scripting Languages preprocessor before compilation interpreter vs. compiler -s enable switch parsing efficiency concerns -S makes Perl use the PATH environment strong typed vs. type-less variable to search for the script Perl: Practical Extraction and Report Language -T forces taint checks to be turned on so pattern matching capability you can test them -u causes Perl to dump core after Resources compiling your script Unix Perl manpages -U allow Perl to do unsafe operations Usenet newsgroups: comp.lang.perl -v print version Perl homepage: http://www.perl/com/perl/, http://www.perl.org -V print Perl configuration and @INC Download: http://www.perl.com/CPAN/ values -V:<name> print the value of the named To Run Perl Script configuration value run as command: perl –e ‘print “Hello, world!\n”;’ -w print warning for unused variable, run as scripts (with chmod +x): perl <script> using variable without setting the #!/usr/local/bin/perl –w value, undefined functions, references use strict; to undefined filehandle, write to print “Hello, world!\n”; filehandle which is read-only, using a exit 0; non-number as it were a number, or switches subroutine recurse too deep, etc. -

Compilers History of Compilers
Compilers A compiler allows programmers to ignore the Compilers are fundamental to machine-dependent details of modern computing. programming. They act as translators, transforming human-oriented Compilers allow programs and programming languages into programming skills to be computer-oriented machine machine-independent. languages. To most users, a compiler can be viewed as a “black box” that Compilers also aid in detecting performs the transformation programming errors (which are shown below. all too common). Compiler techniques also help to improve computer security. Programming Language Compiler Machine Language For example, the Java Bytecode Verifier helps to guarantee that Java security rules are satisfied. © © CS 536 Spring 2008 10 CS 536 Spring 2008 11 Compilers currently help in History of Compilers protection of intellectual property (using obfuscation) The term compiler was coined and provenance (through in the early 1950s by Grace watermarking). Murray Hopper. Translation was viewed as the “compilation” of a sequence of machine- language subprograms selected from a library. One of the first real compilers was the FORTRAN compiler of the late 1950s. It allowed a programmer to use a problem- oriented source language. © © CS 536 Spring 2008 12 CS 536 Spring 2008 13 Ambitious “optimizations” were Compilers Enable used to produce efficient Programming Languages machine code, which was vital for early computers with quite Programming languages are limited capabilities. used for much more than “ordinary” computation. Efficient use of machine • TeX and LaTeX use compilers to translate text and formatting resources is still an essential commands into intricate requirement for modern typesetting commands. compilers. • Postscript, generated by text- formatters like LaTeX, Word, and FrameMaker, is really a programming language. -
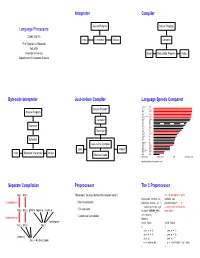
Language Processors Interpreter Compiler Bytecode Interpreter Just
Interpreter Compiler Source Program Source Program Language Processors COMS W4115 Input Interpreter Output Compiler Prof. Stephen A. Edwards Fall 2004 Columbia University Input Executable Program Output Department of Computer Science Bytecode Interpreter Just-in-time Compiler Language Speeds Compared Language Impl. C gcc Source Program Ocaml ocaml SML mlton Source Program C++ g++ SML smlnj Common Lisp cmucl Scheme bigloo Ocaml ocamlb Compiler Java java Pike pike Forth gforth Lua lua Compiler Python python Perl perl Ruby ruby Bytecode Eiffel se Mercury mercury Awk mawk Haskell ghc Lisp rep Icon icon Bytecode Tcl tcl Javascript njs Scheme guile Just-in-time Compiler Forth bigforth Erlang erlang Awk gawk Input Output Emacs Lisp xemacs Scheme stalin Input Bytecode Interpreter Output PHP php Machine Code Bash bash bytecodes native code JIT Threaded code http://www.bagley.org/˜doug/shootout/ Separate Compilation Preprocessor The C Preprocessor foo.c bar.c “Massages” the input before the compiler sees it. cc -E example.c gives #include <stdio.h> extern int C compiler cc: • Macro expansion #define min(x, y) \ printf(char*,...); ((x)<(y))?(x):(y) ... many more declarations • foo.s bar.s printf.o fopen.o malloc.o · · · File inclusion #ifdef DEFINE_BAZ from stdio.h • Conditional compilation int baz(); Assembler as: #endif Archiver ar: void foo() void foo() · · · foo.o bar.o libc.a { { int a = 1; int a = 1; int b = 2; int b = 2; Linker ld: int c; int c; foo — An Executable c = min(a,b); c = ((a)<(b))?(a):(b); } } Compiling a Simple Program What the -

A Hybrid Approach of Compiler and Interpreter Achal Aggarwal, Dr
International Journal of Scientific & Engineering Research, Volume 5, Issue 6, June-2014 1022 ISSN 2229-5518 A Hybrid Approach of Compiler and Interpreter Achal Aggarwal, Dr. Sunil K. Singh, Shubham Jain Abstract— This paper essays the basic understanding of compiler and interpreter and identifies the need of compiler for interpreted languages. It also examines some of the recent developments in the proposed research. Almost all practical programs today are written in higher-level languages or assembly language, and translated to executable machine code by a compiler and/or assembler and linker. Most of the interpreted languages are in demand due to their simplicity but due to lack of optimization, they require comparatively large amount of time and space for execution. Also there is no method for code minimization; the code size is larger than what actually is needed due to redundancy in code especially in the name of identifiers. Index Terms— compiler, interpreter, optimization, hybrid, bandwidth-utilization, low source-code size. —————————— —————————— 1 INTRODUCTION order to reduce the complexity of designing and building • Compared to machine language, the notation used by Icomputers, nearly all of these are made to execute relatively programming languages closer to the way humans simple commands (but do so very quickly). A program for a think about problems. computer must be built by combining some very simple com- • The compiler can spot some obvious programming mands into a program in what is called machine language. mistakes. Since this is a tedious and error prone process most program- • Programs written in a high-level language tend to be ming is, instead, done using a high-level programming lan- shorter than equivalent programs written in machine guage. -

Basics of Compiler Design
Basics of Compiler Design Anniversary edition Torben Ægidius Mogensen DEPARTMENT OF COMPUTER SCIENCE UNIVERSITY OF COPENHAGEN Published through lulu.com. c Torben Ægidius Mogensen 2000 – 2010 [email protected] Department of Computer Science University of Copenhagen Universitetsparken 1 DK-2100 Copenhagen DENMARK Book homepage: http://www.diku.dk/∼torbenm/Basics First published 2000 This edition: August 20, 2010 ISBN 978-87-993154-0-6 Contents 1 Introduction 1 1.1 What is a compiler? . 1 1.2 The phases of a compiler . 2 1.3 Interpreters . 3 1.4 Why learn about compilers? . 4 1.5 The structure of this book . 5 1.6 To the lecturer . 6 1.7 Acknowledgements . 7 1.8 Permission to use . 7 2 Lexical Analysis 9 2.1 Introduction . 9 2.2 Regular expressions . 10 2.2.1 Shorthands . 13 2.2.2 Examples . 14 2.3 Nondeterministic finite automata . 15 2.4 Converting a regular expression to an NFA . 18 2.4.1 Optimisations . 20 2.5 Deterministic finite automata . 22 2.6 Converting an NFA to a DFA . 23 2.6.1 Solving set equations . 23 2.6.2 The subset construction . 26 2.7 Size versus speed . 29 2.8 Minimisation of DFAs . 30 2.8.1 Example . 32 2.8.2 Dead states . 34 2.9 Lexers and lexer generators . 35 2.9.1 Lexer generators . 41 2.10 Properties of regular languages . 42 2.10.1 Relative expressive power . 42 2.10.2 Limits to expressive power . 44 i ii CONTENTS 2.10.3 Closure properties . 45 2.11 Further reading .