Gradient, Divergence, Curl and Related Formulae
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

General Relativity Fall 2018 Lecture 10: Integration, Einstein-Hilbert Action
General Relativity Fall 2018 Lecture 10: Integration, Einstein-Hilbert action Yacine Ali-Ha¨ımoud (Dated: October 3, 2018) σ σ HW comment: T µν antisym in µν does NOT imply that Tµν is antisym in µν. Volume element { Consider a LICS with primed coordinates. The 4-volume element is dV = d4x0 = 0 0 0 0 dx0 dx1 dx2 dx3 . If we change coordinates, we have 0 ! @xµ d4x0 = det d4x: (1) µ @x Now, the metric components change as 0 0 0 0 @xµ @xν @xµ @xν g = g 0 0 = η 0 0 ; (2) µν @xµ @xν µ ν @xµ @xν µ ν since the metric components are ηµ0ν0 in the LICS. Seing this as a matrix operation and taking the determinant, we find 0 !2 @xµ det(g ) = − det : (3) µν @xµ Hence, we find that the 4-volume element is q 4 p 4 p 4 dV = − det(gµν )d x ≡ −g d x ≡ jgj d x: (4) The integral of a scalar function f is well defined: given any coordinate system (even if only defined locally): Z Z f dV = f pjgj d4x: (5) We can only define the integral of a scalar function. The integral of a vector or tensor field is mean- ingless in curved spacetime. Think of the integral as a sum. To sum vectors, you need them to belong to the same vector space. There is no common vector space in curved spacetime. Only in flat spacetime can we define such integrals. First parallel-transport the vector field to a single point of spacetime (it doesn't matter which one). -

College Summit, Inc. D/B/A Peerforward Financial Statements
College Summit, Inc. d/b/a PeerForward Financial Statements For the Years Ended April 30, 2020 and 2019 and Report Thereon COLLEGE SUMMIT, INC. d/b/a PeerForward TABLE OF CONTENTS For the Years Ended April 30, 2020 and 2019 _______________ Page Independent Auditors’ Report ............................................................................................................. 1-2 Financial Statements Statements of Financial Position ........................................................................................................ 3 Statements of Activities ...................................................................................................................... 4 Statements of Functional Expenses ................................................................................................ 5-6 Statements of Cash Flows .................................................................................................................. 7 Notes to Financial Statements ....................................................................................................... 8-17 INDEPENDENT AUDITORS’ REPORT To the Board of Directors of College Summit, Inc. d/b/a PeerForward Report on the Financial Statements We have audited the accompanying financial statements of College Summit, Inc. d/b/a PeerForward (PeerForward), which comprise the statements of financial position as of April 30, 2020 and 2019, and the related statements of activities, functional expenses and cash flows for the years then ended, and the related notes -

How Can We Create Environments Where Hate Cannot Flourish?
How can we create environments where hate cannot flourish? Saturday, February 1 9:30 a.m. – 10:00 a.m. Check-In and Registration Location: Field Museum West Entrance 10:00 a.m. – 10:30 a.m. Introductions and Program Kick-Off JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1 10:30 a.m. – 11:30 a.m. Watch “The Path to Nazi Genocide” and Reflections JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1 11:30 a.m. – 11:45 a.m. Break and walk to State of Deception 11:45 a.m. – 12:30 p.m. Visit State of Deception Interpretation by Holocaust Survivor Volunteers from the Illinois Holocaust Museum Location: Upper level 12:30 p.m. – 1:00 p.m. Breakout Session: Reflections on Exhibit Tim Kaiser, USHMM Director, Education Initiatives David Klevan, USHMM Digital Learning Strategist JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1, Classrooms A and B Saturday, February 2 (continued) 1:00 p.m. – 1:45 p.m. Lunch 1:45 p.m. – 2:45 p.m. A Survivor’s Personal Story Bob Behr, USHMM Survivor Volunteer Interviewed by: Ann Weber, USHMM Program Coordinator Location: Lecture Hall 1 2:45 p.m. – 3:00 p.m. Break 3:00 p.m. – 3:45 p.m. Student Panel: Beyond Indifference Location: Lecture Hall 1 Moderator: Emma Pettit, Sustained Dialogue Campus Network Student/Alumni Panelists: Jazzy Johnson, Northwestern University Mary Giardina, The Ohio State University Nory Kaplan-Kelly, University of Chicago 3:45 p.m. – 4:30 p.m. Breakout Session: Sharing Personal Reflections Tim Kaiser, USHMM Director, Education Initiatives David Klevan, USHMM Digital Learning Strategist JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1, Classrooms A and B 4:30 p.m. -

Stroke Training for EMS Professionals (PDF)
STROKE TRAINING FOR EMS PROFESSIONALS 1 COURSE OBJECTIVES About Stroke Stroke Policy Recommendations Stroke Protocols and Stroke Hospital Care Stroke Assessment Tools Pre-Notification Stroke Treatment ABOUT STROKE STROKE FACTS • A stroke is a medical emergency! Stroke occurs when blood flow is either cut off or is reduced, depriving the brain of blood and oxygen • Approximately 795,000 strokes occur in the US each year • Stroke is the fifth leading cause of death in the US • Stroke is a leading cause of adult disability • On average, every 40 seconds, someone in the United States has a stroke • Over 4 million stroke survivors are in the US • The indirect and direct cost of stroke: $38.6 billion annually (2009) • Crosses all ethnic, racial and socioeconomic groups Berry, Jarett D., et al. Heart Disease and Stroke Statistics --2013 Update: A Report from the American Heart Association. Circulation. 127, 2013. DIFFERENT TYPES OF STROKE Ischemic Stroke • Caused by a blockage in an artery stopping normal blood and oxygen flow to the brain • 87% of strokes are ischemic • There are two types of ischemic strokes: Embolism: Blood clot or plaque fragment from elsewhere in the body gets lodged in the brain Thrombosis: Blood clot formed in an artery that provides blood to the brain Berry, Jarett D., et al. Heart Disease and Stroke Statistics --2013 Update: A Report from the American Heart Association. Circulation. 127, 2013. http://www.strokeassociation.org/STROKEORG/AboutStroke/TypesofStroke/IschemicClots/Ischemic-Strokes- Clots_UCM_310939_Article.jsp -

Vector Calculus and Multiple Integrals Rob Fender, HT 2018
Vector Calculus and Multiple Integrals Rob Fender, HT 2018 COURSE SYNOPSIS, RECOMMENDED BOOKS Course syllabus (on which exams are based): Double integrals and their evaluation by repeated integration in Cartesian, plane polar and other specified coordinate systems. Jacobians. Line, surface and volume integrals, evaluation by change of variables (Cartesian, plane polar, spherical polar coordinates and cylindrical coordinates only unless the transformation to be used is specified). Integrals around closed curves and exact differentials. Scalar and vector fields. The operations of grad, div and curl and understanding and use of identities involving these. The statements of the theorems of Gauss and Stokes with simple applications. Conservative fields. Recommended Books: Mathematical Methods for Physics and Engineering (Riley, Hobson and Bence) This book is lazily referred to as “Riley” throughout these notes (sorry, Drs H and B) You will all have this book, and it covers all of the maths of this course. However it is rather terse at times and you will benefit from looking at one or both of these: Introduction to Electrodynamics (Griffiths) You will buy this next year if you haven’t already, and the chapter on vector calculus is very clear Div grad curl and all that (Schey) A nice discussion of the subject, although topics are ordered differently to most courses NB: the latest version of this book uses the opposite convention to polar coordinates to this course (and indeed most of physics), but older versions can often be found in libraries 1 Week One A review of vectors, rotation of coordinate systems, vector vs scalar fields, integrals in more than one variable, first steps in vector differentiation, the Frenet-Serret coordinate system Lecture 1 Vectors A vector has direction and magnitude and is written in these notes in bold e.g. -

Lecture 9: Partial Derivatives
Math S21a: Multivariable calculus Oliver Knill, Summer 2016 Lecture 9: Partial derivatives ∂ If f(x,y) is a function of two variables, then ∂x f(x,y) is defined as the derivative of the function g(x) = f(x,y) with respect to x, where y is considered a constant. It is called the partial derivative of f with respect to x. The partial derivative with respect to y is defined in the same way. ∂ We use the short hand notation fx(x,y) = ∂x f(x,y). For iterated derivatives, the notation is ∂ ∂ similar: for example fxy = ∂x ∂y f. The meaning of fx(x0,y0) is the slope of the graph sliced at (x0,y0) in the x direction. The second derivative fxx is a measure of concavity in that direction. The meaning of fxy is the rate of change of the slope if you change the slicing. The notation for partial derivatives ∂xf,∂yf was introduced by Carl Gustav Jacobi. Before, Josef Lagrange had used the term ”partial differences”. Partial derivatives fx and fy measure the rate of change of the function in the x or y directions. For functions of more variables, the partial derivatives are defined in a similar way. 4 2 2 4 3 2 2 2 1 For f(x,y)= x 6x y + y , we have fx(x,y)=4x 12xy ,fxx = 12x 12y ,fy(x,y)= − − − 12x2y +4y3,f = 12x2 +12y2 and see that f + f = 0. A function which satisfies this − yy − xx yy equation is also called harmonic. The equation fxx + fyy = 0 is an example of a partial differential equation: it is an equation for an unknown function f(x,y) which involves partial derivatives with respect to more than one variables. -

Mathematical Theorems
Appendix A Mathematical Theorems The mathematical theorems needed in order to derive the governing model equations are defined in this appendix. A.1 Transport Theorem for a Single Phase Region The transport theorem is employed deriving the conservation equations in continuum mechanics. The mathematical statement is sometimes attributed to, or named in honor of, the German Mathematician Gottfried Wilhelm Leibnitz (1646–1716) and the British fluid dynamics engineer Osborne Reynolds (1842–1912) due to their work and con- tributions related to the theorem. Hence it follows that the transport theorem, or alternate forms of the theorem, may be named the Leibnitz theorem in mathematics and Reynolds transport theorem in mechanics. In a customary interpretation the Reynolds transport theorem provides the link between the system and control volume representations, while the Leibnitz’s theorem is a three dimensional version of the integral rule for differentiation of an integral. There are several notations used for the transport theorem and there are numerous forms and corollaries. A.1.1 Leibnitz’s Rule The Leibnitz’s integral rule gives a formula for differentiation of an integral whose limits are functions of the differential variable [7, 8, 22, 23, 45, 55, 79, 94, 99]. The formula is also known as differentiation under the integral sign. H. A. Jakobsen, Chemical Reactor Modeling, DOI: 10.1007/978-3-319-05092-8, 1361 © Springer International Publishing Switzerland 2014 1362 Appendix A: Mathematical Theorems b(t) b(t) d ∂f (t, x) db da f (t, x) dx = dx + f (t, b) − f (t, a) (A.1) dt ∂t dt dt a(t) a(t) The first term on the RHS gives the change in the integral because the function itself is changing with time, the second term accounts for the gain in area as the upper limit is moved in the positive axis direction, and the third term accounts for the loss in area as the lower limit is moved. -

Medical Terminology Abbreviations Medical Terminology Abbreviations
34 MEDICAL TERMINOLOGY ABBREVIATIONS MEDICAL TERMINOLOGY ABBREVIATIONS The following list contains some of the most common abbreviations found in medical records. Please note that in medical terminology, the capitalization of letters bears significance as to the meaning of certain terms, and is often used to distinguish terms with similar acronyms. @—at A & P—anatomy and physiology ab—abortion abd—abdominal ABG—arterial blood gas a.c.—before meals ac & cl—acetest and clinitest ACLS—advanced cardiac life support AD—right ear ADL—activities of daily living ad lib—as desired adm—admission afeb—afebrile, no fever AFB—acid-fast bacillus AKA—above the knee alb—albumin alt dieb—alternate days (every other day) am—morning AMA—against medical advice amal—amalgam amb—ambulate, walk AMI—acute myocardial infarction amt—amount ANS—automatic nervous system ant—anterior AOx3—alert and oriented to person, time, and place Ap—apical AP—apical pulse approx—approximately aq—aqueous ARDS—acute respiratory distress syndrome AS—left ear ASA—aspirin asap (ASAP)—as soon as possible as tol—as tolerated ATD—admission, transfer, discharge AU—both ears Ax—axillary BE—barium enema bid—twice a day bil, bilateral—both sides BK—below knee BKA—below the knee amputation bl—blood bl wk—blood work BLS—basic life support BM—bowel movement BOW—bag of waters B/P—blood pressure bpm—beats per minute BR—bed rest MEDICAL TERMINOLOGY ABBREVIATIONS 35 BRP—bathroom privileges BS—breath sounds BSI—body substance isolation BSO—bilateral salpingo-oophorectomy BUN—blood, urea, nitrogen -
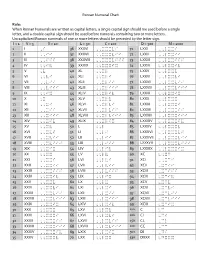
Roman Numeral Chart
Roman Numeral Chart Rule: When Roman Numerals are written as capital letters, a single capital sign should me used before a single letter, and a double capital sign should be used before numerals containing two or more letters. Uncapitalized Roman numerals of one or more letters should be preceded by the letter sign. I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1000 1 I ,I 36 XXXVI ,,XXXVI 71 LXXI ,,LXXI 2 II ,,II 37 XXXVII ,,XXXVII 72 LXXII ,,LXXII 3 III ,,III 38 XXXVIII ,,XXXVIII 73 LXXIII ,,LXXIII 4 IV ,,IV 39 XXXIX ,,XXXIX 74 LXXIV ,,LXXIV 5 V ,V 40 XL ,,XL 75 LXXV ,,LXXV 6 VI ,,VI 41 XLI ,,XLI 76 LXXVI ,,LXXVI 7 VII ,,VII 42 XLII ,,XLII 77 LXXVII ,,LXXVII 8 VIII ,,VIII 43 XLIII ,,XLIII 78 LXXVIII ,,LXXVIII 9 IX ,,IX 44 XLIV ,,XLIV 79 LXXIX ,,LXXIX 10 X ,X 45 XLV ,,XLV 80 LXXX ,,LXXX 11 XI ,,XI 46 XLVI ,,XLVI 81 LXXXI ,,LXXXI 12 XII ,,XII 47 XLVII ,,XLVII 82 LXXXII ,,LXXXII 13 XIII ,,XIII 48 XLVIII ,,XLVIII 83 LXXXIII ,,LXXXIII 14 XIV ,,XIV 49 XLIX ,,XLIX 84 LXXXIV ,,LXXXIV 15 XV ,,XV 50 L ,,L 85 LXXXV ,,LXXXV 16 XVI ,,XVI 51 LI ,,LI 86 LXXXVI ,,LXXXVI 17 XVII ,,XVII 52 LII ,,LII 87 LXXXVII ,,LXXXVII 18 XVIII ,,XVIII 53 LIII ,,LIII 88 LXXXVIII ,,LXXXVIII 19 XIX ,,XIX 54 LIV ,,LIV 89 LXXXIX ,,LXXXIX 20 XX ,,XX 55 LV ,,LV 90 XC ,,XC 21 XXI ,,XXI 56 LVI ,,LVI 91 XCI ,,XCI 22 XXII ,,XXII 57 LVII ,,LVII 92 XCII ,XCII 23 XXIII ,,XXIII 58 LVIII ,,LVIII 93 XCIII ,XCIII 24 XXIV ,,XXIV 59 LIX ,,LIX 94 XCIV ,XCIV 25 XXV ,,XXV 60 LX ,,LX 95 XCV ,XCV 26 XXVI ,,XXVI 61 LXI ,,LXI 96 XCVI ,XCVI 27 XXVII ,,XXVII 62 LXII ,,LXII 97 XCVII ,XCVII 28 XXVIII ,,XXVIII 63 LXIII ,,LXIII 98 XCVIII ,XCVIII 29 XXIX ,,XXIX 64 LXIV ,,LXIV 99 XCIX ,XCIX 30 XXX ,,XXX 65 LXV ,,LXV 100 C ,C 31 XXXI ,,XXXI 66 LXVI ,,LXVI 101 CI ,CI 32 XXXII ,,XXXII 67 LXVII ,,LXVII 150 CL ,CL 33 XXXIII ,,XXXIII 68 LXVIII ,,LXVIII 200 CC ,CC 34 XXXIV ,,XXXIV 69 LXIX ,,LXIX 501 DI ,DI 35 XXXV ,,XXXV 70 LXX ,,LXX 530 DXXX ,DXXX . -

Policy Gradient
Lecture 7: Policy Gradient Lecture 7: Policy Gradient David Silver Lecture 7: Policy Gradient Outline 1 Introduction 2 Finite Difference Policy Gradient 3 Monte-Carlo Policy Gradient 4 Actor-Critic Policy Gradient Lecture 7: Policy Gradient Introduction Policy-Based Reinforcement Learning In the last lecture we approximated the value or action-value function using parameters θ, V (s) V π(s) θ ≈ Q (s; a) Qπ(s; a) θ ≈ A policy was generated directly from the value function e.g. using -greedy In this lecture we will directly parametrise the policy πθ(s; a) = P [a s; θ] j We will focus again on model-free reinforcement learning Lecture 7: Policy Gradient Introduction Value-Based and Policy-Based RL Value Based Learnt Value Function Implicit policy Value Function Policy (e.g. -greedy) Policy Based Value-Based Actor Policy-Based No Value Function Critic Learnt Policy Actor-Critic Learnt Value Function Learnt Policy Lecture 7: Policy Gradient Introduction Advantages of Policy-Based RL Advantages: Better convergence properties Effective in high-dimensional or continuous action spaces Can learn stochastic policies Disadvantages: Typically converge to a local rather than global optimum Evaluating a policy is typically inefficient and high variance Lecture 7: Policy Gradient Introduction Rock-Paper-Scissors Example Example: Rock-Paper-Scissors Two-player game of rock-paper-scissors Scissors beats paper Rock beats scissors Paper beats rock Consider policies for iterated rock-paper-scissors A deterministic policy is easily exploited A uniform random policy -

Introduction to Shape Optimization
Introduction to Shape optimization Noureddine Igbida1 1Institut de recherche XLIM, UMR-CNRS 6172, Facult´edes Sciences et Techniques, Universit´ede Limoges 123, Avenue Albert Thomas 87060 Limoges, France. Email : [email protected] Preliminaries on PDE 1 Contents 1. PDE ........................................ 2 2. Some differentiation and differential operators . 3 2.1 Gradient . 3 2.2 Divergence . 4 2.3 Curl . 5 2 2.4 Remarks . 6 2.5 Laplacian . 7 2.6 Coordinate expressions of the Laplacian . 10 3. Boundary value problem . 12 4. Notion of solution . 16 1. PDE A mathematical model is a description of a system using mathematical language. The process of developing a mathematical model is termed mathematical modelling (also written model- ing). Mathematical models are used in many area, as in the natural sciences (such as physics, biology, earth science, meteorology), engineering disciplines (e.g. computer science, artificial in- telligence), in the social sciences (such as economics, psychology, sociology and political science); Introduction to Shape optimization N. Igbida physicists, engineers, statisticians, operations research analysts and economists. Among this mathematical language we have PDE. These are a type of differential equation, i.e., a relation involving an unknown function (or functions) of several independent variables and their partial derivatives with respect to those variables. Partial differential equations are used to formulate, and thus aid the solution of, problems involving functions of several variables; such as the propagation of sound or heat, electrostatics, electrodynamics, fluid flow, and elasticity. Seemingly distinct physical phenomena may have identical mathematical formulations, and thus be governed by the same underlying dynamic. In this section, we give some basic example of elliptic partial differential equation (PDE) of second order : standard Laplacian and Laplacian with variable coefficients. -

Vector Calculus and Differential Forms with Applications To
Vector Calculus and Differential Forms with Applications to Electromagnetism Sean Roberson May 7, 2015 PREFACE This paper is written as a final project for a course in vector analysis, taught at Texas A&M University - San Antonio in the spring of 2015 as an independent study course. Students in mathematics, physics, engineering, and the sciences usually go through a sequence of three calculus courses before go- ing on to differential equations, real analysis, and linear algebra. In the third course, traditionally reserved for multivariable calculus, stu- dents usually learn how to differentiate functions of several variable and integrate over general domains in space. Very rarely, as was my case, will professors have time to cover the important integral theo- rems using vector functions: Green’s Theorem, Stokes’ Theorem, etc. In some universities, such as UCSD and Cornell, honors students are able to take an accelerated calculus sequence using the text Vector Cal- culus, Linear Algebra, and Differential Forms by John Hamal Hubbard and Barbara Burke Hubbard. Here, students learn multivariable cal- culus using linear algebra and real analysis, and then they generalize familiar integral theorems using the language of differential forms. This paper was written over the course of one semester, where the majority of the book was covered. Some details, such as orientation of manifolds, topology, and the foundation of the integral were skipped to save length. The paper should still be readable by a student with at least three semesters of calculus, one course in linear algebra, and one course in real analysis - all at the undergraduate level.