Analytically Differentiable Dynamics for Multi-Body Systems with Frictional Contact
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Ian R. Porteous 9 October 1930 - 30 January 2011
In Memoriam Ian R. Porteous 9 October 1930 - 30 January 2011 A tribute by Peter Giblin (University of Liverpool) Będlewo, Poland 16 May 2011 Caustics 1998 Bill Bruce, disguised as a Terry Wall, ever a Pro-Vice-Chancellor mathematician Watch out for Bruce@60, Wall@75, Liverpool, June 2012 with Christopher Longuet-Higgins at the Rank Prize Funds symposium on computer vision in Liverpool, summer 1987, jointly organized by Ian, Joachim Rieger and myself After a first degree at Edinburgh and National Service, Ian worked at Trinity College, Cambridge, for a BA then a PhD under first William Hodge, but he was about to become Secretary of the Royal Society and Master of Pembroke College Cambridge so when Michael Atiyah returned from Princeton in January 1957 he took on Ian and also Rolph Schwarzenberger (6 years younger than Ian) as PhD students Ian’s PhD was in algebraic geometry, the effect of blowing up on Chern Classes, published in Proceedings of the Cambridge Philosophical Society in 1960: The behaviour of the Chern classes or of the canonical classes of an algebraic variety under a dilatation has been studied by several authors (Todd, Segre, van de Ven). This problem is of interest since a dilatation is the simplest form of birational transformation which does not preserve the underlying topological structure of the algebraic variety. A relation between the Chern classes of the variety obtained by dilatation of a subvariety and the Chern classes of the original variety has been conjectured by the authors cited above but a complete proof of this relation is not in the literature. -

Evolutes of Curves in the Lorentz-Minkowski Plane
Evolutes of curves in the Lorentz-Minkowski plane 著者 Izumiya Shuichi, Fuster M. C. Romero, Takahashi Masatomo journal or Advanced Studies in Pure Mathematics publication title volume 78 page range 313-330 year 2018-10-04 URL http://hdl.handle.net/10258/00009702 doi: info:doi/10.2969/aspm/07810313 Evolutes of curves in the Lorentz-Minkowski plane S. Izumiya, M. C. Romero Fuster, M. Takahashi Abstract. We can use a moving frame, as in the case of regular plane curves in the Euclidean plane, in order to define the arc-length parameter and the Frenet formula for non-lightlike regular curves in the Lorentz- Minkowski plane. This leads naturally to a well defined evolute asso- ciated to non-lightlike regular curves without inflection points in the Lorentz-Minkowski plane. However, at a lightlike point the curve shifts between a spacelike and a timelike region and the evolute cannot be defined by using this moving frame. In this paper, we introduce an alternative frame, the lightcone frame, that will allow us to associate an evolute to regular curves without inflection points in the Lorentz- Minkowski plane. Moreover, under appropriate conditions, we shall also be able to obtain globally defined evolutes of regular curves with inflection points. We investigate here the geometric properties of the evolute at lightlike points and inflection points. x1. Introduction The evolute of a regular plane curve is a classical subject of differen- tial geometry on Euclidean plane which is defined to be the locus of the centres of the osculating circles of the curve (cf. [3, 7, 8]). -

The Illinois Mathematics Teacher
THE ILLINOIS MATHEMATICS TEACHER EDITORS Marilyn Hasty and Tammy Voepel Southern Illinois University Edwardsville Edwardsville, IL 62026 REVIEWERS Kris Adams Chip Day Karen Meyer Jean Smith Edna Bazik Lesley Ebel Jackie Murawska Clare Staudacher Susan Beal Dianna Galante Carol Nenne Joe Stickles, Jr. William Beggs Linda Gilmore Jacqueline Palmquist Mary Thomas Carol Benson Linda Hankey James Pelech Bob Urbain Patty Bruzek Pat Herrington Randy Pippen Darlene Whitkanack Dane Camp Alan Holverson Sue Pippen Sue Younker Bill Carroll John Johnson Anne Marie Sherry Mike Carton Robin Levine-Wissing Aurelia Skiba ICTM GOVERNING BOARD 2012 Don Porzio, President Rich Wyllie, Treasurer Fern Tribbey, Past President Natalie Jakucyn, Board Chair Lannette Jennings, Secretary Ann Hanson, Executive Director Directors: Mary Modene, Catherine Moushon, Early Childhood (2009-2012) Com. College/Univ. (2010-2013) Polly Hill, Marshall Lassak, Early Childhood (2011-2014) Com. College/Univ. (2011-2014) Cathy Kaduk, George Reese, 5-8 (2010-2013) Director-At-Large (2009-2012) Anita Reid, Natalie Jakucyn, 5-8 (2011-2014) Director-At-Large (2010-2013) John Benson, Gwen Zimmermann, 9-12 (2009-2012) Director-At-Large (2011-2014) Jerrine Roderique, 9-12 (2010-2013) The Illinois Mathematics Teacher is devoted to teachers of mathematics at ALL levels. The contents of The Illinois Mathematics Teacher may be quoted or reprinted with formal acknowledgement of the source and a letter to the editor that a quote has been used. The activity pages in this issue may be reprinted for classroom use without written permission from The Illinois Mathematics Teacher. (Note: Occasionally copyrighted material is used with permission. Such material is clearly marked and may not be reprinted.) THE ILLINOIS MATHEMATICS TEACHER Volume 61, No. -

Some Remarks on Duality in S3
GEOMETRY AND TOPOLOGY OF CAUSTICS — CAUSTICS ’98 BANACH CENTER PUBLICATIONS, VOLUME 50 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 1999 SOME REMARKS ON DUALITY IN S 3 IAN R. PORTEOUS Department of Mathematical Sciences University of Liverpool Liverpool, L69 3BX, UK e-mail: [email protected] Abstract. In this paper we review some of the concepts and results of V. I. Arnol0d [1] for curves in S2 and extend them to curves and surfaces in S3. 1. Introduction. In [1] Arnol0d introduces the concepts of the dual curve and the derivative curve of a smooth (= C1) embedded curve in S2. In particular he shows that the evolute or caustic of such a curve is the dual of the derivative. The dual curve is just the unit normal curve, while the derivative is the unit tangent curve. The definitions extend in an obvious way to curves on S2 with ordinary cusps. Then one proves easily that where a curve has an ordinary geodesic inflection the dual has an ordinary cusp and vice versa. Since the derivative of a curve without cusps clearly has no cusps it follows that the caustic of such a curve has no geodesic inflections. This prompts investigating what kind of singularity a curve must have for its caustic to have a geodesic inflection, by analogy with the classical construction of de l'H^opital,see [2], pages 24{26. In the second and third parts of the paper the definitions of Arnol0d are extended to surfaces in S3 and to curves in S3. The notations are those of Porteous [2], differentiation being indicated by subscripts. -

A Convex, Smooth and Invertible Contact Model for Trajectory Optimization
A convex, smooth and invertible contact model for trajectory optimization Emanuel Todorov Departments of Applied Mathematics and Computer Science and Engineering University of Washington Abstract— Trajectory optimization is done most efficiently There is however one additional requirement which we when an inverse dynamics model is available. Here we develop believe is essential and requires a qualitatively new approach: the first model of contact dynamics definedinboththeforward iv. The contact model should be defined for both forward and and inverse directions. The contact impulse is the solution to a convex optimization problem: minimize kinetic energy inverse dynamics. Here the forward dynamics in contact space subject to non-penetration and friction-cone w = a (q w u ) (1) constraints. We use a custom interior-point method to make the +1 1 optimization problem unconstrained; this is key to defining the compute the next-step velocity w+1 given the current forward and inverse dynamics in a consistent way. The resulting generalized position q , velocity w and applied force u , model has a parameter which sets the amount of contact smoothing, facilitating continuation methods for optimization. while the inverse dynamics We implemented the proposed contact solver in our new physics u = b (q w w ) (2) engine (MuJoCo). A full Newton step of trajectory optimization +1 for a 3D walking gait takes only 160 msec, on a 12-core PC. compute the applied force that caused the observed change in velocity. Computing the total force that caused the observed I. INTRODUCTION change in velocity is of course straightforward. The hard Optimal control theory provides a powerful set of methods part is decomposing this total force into a contact force and for planning and automatic control. -

Mathematics 1
Mathematics 1 MATHEMATICS Courses MATH 1483 Mathematical Functions and Their Uses (A) Math is the language of science and a vital part of both cutting-edge Prerequisites: An acceptable placement score - see research and daily life. Contemporary mathematics investigates such placement.okstate.edu. basic concepts as space and number and also the formulation and Description: Analysis of functions and their graphs from the viewpoint analysis of mathematical models arising from applications. Mathematics of rates of change. Linear, exponential, logarithmic and other functions. has always had close relationships to the physical sciences and Applications to the natural sciences, agriculture, business and the social engineering. As the biological, social, and management sciences have sciences. become increasingly quantitative, the mathematical sciences have Credit hours: 3 moved in new directions to support these fields. Contact hours: Lecture: 3 Contact: 3 Levels: Undergraduate Mathematicians teach in high schools and colleges, do research and Schedule types: Lecture teach at universities, and apply mathematics in business, industry, Department/School: Mathematics and government. Outside of education, mathematicians usually work General Education and other Course Attributes: Analytical & Quant in research and analytical positions, although they have become Thought increasingly involved in management. Firms in the aerospace, MATH 1493 Applications of Modern Mathematics (A) communications, computer, defense, electronics, energy, finance, and Prerequisites: An acceptable placement score (see insurance industries employ many mathematicians. In such employment, placement.okstate.edu). a mathematician typically serves either in a consulting capacity, giving Description: Introduction to contemporary applications of discrete advice on mathematical problems to engineers and scientists, or as a mathematics. Topics from management science, statistics, coding and member of a research team composed of specialists in several fields. -
Geometric Differentiation: for the Intelligence of Curves and Surfaces: Second Edition I
Cambridge University Press 978-0-521-81040-1 - Geometric Differentiation: For the intelligence of Curves and Surfaces: Second Edition I. R. Porteous Frontmatter More information Geometric differentiation © in this web service Cambridge University Press www.cambridge.org Cambridge University Press 978-0-521-81040-1 - Geometric Differentiation: For the intelligence of Curves and Surfaces: Second Edition I. R. Porteous Frontmatter More information © in this web service Cambridge University Press www.cambridge.org Cambridge University Press 978-0-521-81040-1 - Geometric Differentiation: For the intelligence of Curves and Surfaces: Second Edition I. R. Porteous Frontmatter More information Geometric differentiation for the intelligence of curves and surfaces Second edition I. R. Porteous Senior Lecturer, Department of Pure Mathematics University of Liverpool © in this web service Cambridge University Press www.cambridge.org Cambridge University Press 978-0-521-81040-1 - Geometric Differentiation: For the intelligence of Curves and Surfaces: Second Edition I. R. Porteous Frontmatter More information University Printing House, Cambridge CB2 8BS, United Kingdom Cambridge University Press is part of the University of Cambridge. It furthers the University’s mission by disseminating knowledge in the pursuit of education, learning and research at the highest international levels of excellence. www.cambridge.org Information on this title: www.cambridge.org/9780521810401 © Cambridge University Press 1994, 2001 This publication is in copyright. Subject -

Differential Geometry from a Singularity Theory Viewpoint
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Biblioteca Digital da Produção Intelectual da Universidade de São Paulo (BDPI/USP) Universidade de São Paulo Biblioteca Digital da Produção Intelectual - BDPI Departamento de Matemática - ICMC/SMA Livros e Capítulos de Livros - ICMC/SMA 2015-12 Differential geometry from a singularity theory viewpoint IZUMIYA, Shyuichi et al. Differential geometry from a singularity theory viewpoint. Hackensack: World Scientific, 2015. 384 p. http://www.producao.usp.br/handle/BDPI/50103 Downloaded from: Biblioteca Digital da Produção Intelectual - BDPI, Universidade de São Paulo by UNIVERSITY OF SAO PAULO on 03/04/16. For personal use only. Differential Geometry from a Singularity Theory Viewpoint Downloaded www.worldscientific.com 9108_9789814590440_tp.indd 1 22/9/15 9:14 am May 2, 2013 14:6 BC: 8831 - Probability and Statistical Theory PST˙ws This page intentionally left blank by UNIVERSITY OF SAO PAULO on 03/04/16. For personal use only. Differential Geometry from a Singularity Theory Viewpoint Downloaded www.worldscientific.com by UNIVERSITY OF SAO PAULO on 03/04/16. For personal use only. Differential Geometry from a Singularity Theory Viewpoint Downloaded www.worldscientific.com 9108_9789814590440_tp.indd 2 22/9/15 9:14 am Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE Library of Congress Cataloging-in-Publication Data Differential geometry from a singularity theory viewpoint / by Shyuichi Izumiya (Hokkaido University, Japan) [and three others]. -

A Brief Introduction to Singularity Theory (A. Remizov, 2010)
A. O. Remizov A BRIEF INTRODUCTION TO SINGULARITY THEORY Trieste, 2010 1 Lecture 1. Some useful facts from Singularity Theory. Throughout this course all definitions and statements are local, that is, we always operate with ¾sufficiently small¿ neighborhoods of the considered point. In other words, we deal with germs of functioms, maps, vector fields, etc. 1.1 Multiplicity of smooth functions and maps One of the key notions of Singularity Theory is ¾multiplicity¿. Definition 1: Let f(x): R ! R be a smooth (¾smooth¿ means C1) function, and x∗ is its critical point, i.e., f 0(x∗) = 0. Multiplicity of the function f(x) at the critical point x∗ is the order of tangency of the graphs y = f(x) and y = f(x∗) at x∗, i.e., the natural number µ is defined by the condition df dµf dµ+1f (x∗) = 0;:::; (x∗) = 0; (x∗) 6= 0: (1.1) dx dxµ dxµ+1 If such natural number µ does not exist, then we put µ = 1 and the function f(x) − f(x∗) is called ¾1-flat¿ or simply ¾flat¿ at the point x∗. We also put µ = 0 for non-critical points. Critical points with infinite multiplicity can occur, but we will deal only with finite multiplicities. If µ = 1, then the critical point x∗ is called ¾non-degenerated¿. Exercise 1. Prove that any function f with µ < 1 can be simplified to the form f(x) = f(x∗) ± (x − x∗)µ+1 by means of a smooth change of the variable x (the sign ± coincides with the sign of the non-zero derivative in (1.1)). -

In Particular, Line and Sphere Complexes – with Applications to the Theory of Partial Differential Equations
“Ueber Complexe, insbesondere Linien- und Kugel-complexe, mit Anwendung auf die Theorie partieller Differentialgleichungen,” Math. Ann. 5 (1872), 145-208. On complexes −−− in particular, line and sphere complexes – with applications to the theory of partial differential equations By Sophus Lie in CHRISTIANIA Translated by D. H. Delphenich _______ I. The rapid development of geometry in our century is, as is well-known, intimately linked with philosophical arguments about the essence of Cartesian geometry, arguments that were set down in their most general form by Plücker in his early papers. For anyone who proceeds in the spirit of Plücker’s work, the thought that one can employ every curve that depends on three parameters as a space element will convey nothing that is essentially new, so if no one, as far as I know, has pursued this idea then I believe that the reason for this is that no one has ascribed any practical utility to that fact. I was led to study the aforementioned theory when I discovered a remarkable transformation that represented a precise connection between lines of curvature and principal tangent curves, and it is my intention to summarize the results that I obtained in this way in the following treatise. In the first section, I concern myself with curve complexes – that is, manifolds that are composed of a three-fold infinitude of curves. All surfaces that are composed of a single infinitude of curves from a given complex satisfy a partial differential equation of second order that admits a partial differential equation of first order as its singular first integral. -
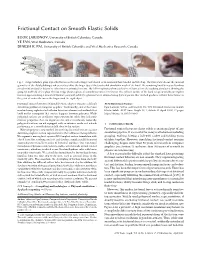
Frictional Contact on Smooth Elastic Solids
Frictional Contact on Smooth Elastic Solids EGOR LARIONOV, University of British Columbia, Canada YE FAN, Vital Mechanics, Canada DINESH K. PAI, University of British Columbia and Vital Mechanics Research, Canada Fig. 1. A rigid whiskey glass is pinched between the index finger and thumb of an animated hand model and lifted up. The first frame shows the internal geometry of the distal phalanges whose vertices drive the finger tips of the tetrahedral simulation mesh of the hand. The remaining hand bones and tendons (not shown) are used to determine other interior animated vertices. The following frames show a selection of frames from the resulting simulation showing the grasp, lift and hold of the glass. The last image shows a photo of a similar scenario for reference. The collision surface of the hand is represented byanimplicit function approximating a smoothed distance potential, while the glass surface is sampled using discrete points. Our method produces realistic deformation at the point of contact between the fingers and the rigid object. Frictional contact between deformable elastic objects remains a difficult ACM Reference Format: simulation problem in computer graphics. Traditionally, contact has been Egor Larionov, Ye Fan, and Dinesh K. Pai. 2021. Frictional Contact on Smooth resolved using sophisticated collision detection schemes and methods that Elastic Solids. ACM Trans. Graph. 40, 2, Article 15 (April 2021), 17 pages. build on the assumption that contact happens between polygons. While https://doi.org/10.1145/3446663 polygonal surfaces are an efficient representation for solids, they lack some intrinsic properties that are important for contact resolution. Generally, polygonal surfaces are not equipped with an intrinsic inside and outside 1 INTRODUCTION partitioning or a smooth distance field close to the surface. -

Contact Singularities in Nonstandard Slow-Fast Dynamical Systems
Contact singularities in nonstandard slow-fast dynamical systems Ian Lizarraga, Robby Marangell, and Martin Wechselberger School of Mathematics and Statistics, University of Sydney, Camperdown 2006, Australia Abstract We develop the contact singularity theory for singularly-perturbed (or ‘slow-fast’) vector fields of the general form z′ = H(z, ε), z Rn and ε 1. Our main result ∈ ≪ is the derivation of computable, coordinate-independent defining equations for contact singularities under an assumption that the leading-order term of the vector field admits a suitable factorization. This factorization can in turn be computed explicitly in a wide variety of applications. We demonstrate these computable criteria by locating contact folds and, for the first time, contact cusps in some nonstandard models of biochemical oscillators. 1 Introduction Classifying the loss of normal hyperbolicity of the critical manifold is a fundamental step in the analysis of slow-fast dynamical systems. For systems in the so-called standard form1 x′ = εg(x,y,ε) y′ = f(x,y,ε), (1) the k-dimensional critical manifold lies inside the zero set of a smooth mapping f(x, y, 0) : Rn Rn−k. Loss of normal hyperbolicity occurs along points where the critical manifold becomes→ tangent to the layer problem of (1), formally defined by the ε 0 limit: → x′ = 0 y′ = f(x, y, 0). (2) In the planar case x, y R, the solutions of the layer flow consist of trajectories lying within vertical lines x = c (also∈ known as fast fibers). In general, solutions of the layer flow lie in arXiv:2004.01825v1 [math.DS] 4 Apr 2020 hyperplanes orthogonal to the coordinate axes of the slow variable x Rk.