Player Pairs Valuation in Ice Hockey
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Head Coach, Tampa Bay Lightning
Table of Contents ADMINISTRATION Team History 270 - 271 All-Time Individual Record 272 - 274 Company Directory 4 - 5 All-Time Team Records 274 - 279 Executives 6 - 11 Scouting Staff 11 - 12 Coaching Staff 13 - 16 PLAYOFF HISTORY & RECORDS Hockey Operations 17 - 20 All-Time Playoff Scoring 282 Broadcast 21 - 22 Playoff Firsts 283 All-Time Playoff Results 284 - 285 2013-14 PLAYER ROSTER Team Playoff Records 286 - 287 Individual Playoff Records 288 - 289 2013-14 Player Roster 23 - 98 Minor League Affiliates 99 - 100 MISCELLANEOUS NHL OPPONENTS In the Community 292 NHL Executives 293 NHL Opponents 109 - 160 NHL Officials and Referees 294 Terms Glossary 295 2013-14 SEASON IN REVIEW Medical Glossary 296 - 298 Broadcast Schedule 299 Final Standings, Individual Leaders, Award Winners 170 - 172 Media Regulations and Policies 300 - 301 Team Statistics, Game-by-Game Results 174 - 175 Frequently Asked Questions 302 - 303 Home and Away Results 190 - 191 Season Summary, Special Teams, Overtime/Shootout 176 - 178 Highs and Lows, Injuries 179 Win / Loss Record 180 HISTORY & RECORDS Season Records 182 - 183 Special Teams 184 Season Leaders 185 All-Time Records 186 - 187 Last Trade With 188 Records vs. Opponents 189 Overtime/Shootout Register 190 - 191 Overtime History 192 Year by Year Streaks 193 All-Time Hat Tricks 194 All-Time Attendance 195 All-Time Shootouts & Penalty Shots 196-197 Best and Worst Record 198 Season Openers and Closers 199 - 201 Year by Year Individual Statistics and Game Results 202 - 243 All-Time Lightning Preseason Results 244 All-Time -
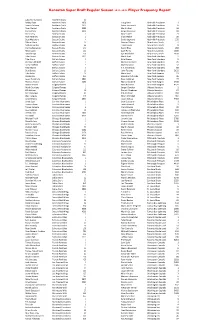
Super Draft Frequency.Xlsx
Kenaston Super Draft Regular Season 2011-2012 Player Frequency Report Lubomir Visnovsky Anaheim Ducks 47 Bobby Ryan Anaheim Ducks 1858 Craig Smith Nashville Predators 1 Teemu Selanne Anaheim Ducks 2410 Patric Hornqvist Nashville Predators 6 Ryan Getzlaf Anaheim Ducks 5089 Martin Erat Nashville Predators 16 Corey Perry Anaheim Ducks 5366 Sergei Kostitsyn Nashville Predators 19 Chris Kelly Boston Bruins 1 Mike Fisher Nashville Predators 21 Rich Peverley Boston Bruins 2 Shea Weber Nashville Predators 26 Brad Marchand Boston Bruins 4 David Legwand Nashville Predators 232 Zdeno Chara Boston Bruins 14 Dainius Zubrus New Jersey Devils 2 Nathan Horton Boston Bruins 60 Travis Zajac New Jersey Devils 8 Patrice Bergeron Boston Bruins 142 Patrik Elias New Jersey Devils 266 Milan Lucic Boston Bruins 144 Zach Parise New Jersey Devils 2189 David Krejci Boston Bruins 150 Ilya Kovalchuk New Jersey Devils 3100 Tyler Seguin Boston Bruins 1011 Mark Streit New York Islanders 2 Tyler Ennis Buffalo Sabres 1 Kyle Okposo New York Islanders 5 Christian Ehrhoff Buffalo Sabres 3 Michael Grabner New York Islanders 25 Drew Stafford Buffalo Sabres 5 Matt Moulson New York Islanders 32 Tyler Myers Buffalo Sabres 9 P.A. Parenteau New York Islanders 58 Brad Boyes Buffalo Sabres 10 John Tavares New York Islanders 5122 Luke Adam Buffalo Sabres 10 Marc Staal New York Rangers 11 Derek Roy Buffalo Sabres 253 Brandon Dubinsky New York Rangers 26 Jason Pominville Buffalo Sabres 2893 Ryan Callahan New York Rangers 77 Thomas Vanek Buffalo Sabres 5280 Marian Gaborik New York Rangers -

Our Online Shop Offers Outlet Nike Football Jersey,Authentic New Nike Jerseys,China Wholesale Cheap Football Jersey,Cheap NHL Je
Our online shop offers Outlet Nike Football Jersey,Authentic new nike jerseys,China wholesale cheap football jersey,Cheap NHL Jerseys.Cheap price and good quality,IF you want to buy good jerseys,click here,Cardinals Jerseys,football jersey creator!Were going to pick up the pace on the NFC South position rankings as we approximate the end We looked along fixed ends Thursday morning and,swiftly were going to transfer onto the broad receivers. In terms of overall strength,nike nfl jersey,new nfl uniforms nike, Id say this position is an of the better ones within the division. But theres a big contention between the Saints,baseball jersey custom, who have a bunch of agreeable receivers to the Panthers,baseball jersey numbers,boise state football jersey, who have only an proven commodity,design your own nfl jersey, to the Buccaneers,nike 2012 nfl, who have lots of potential merely no sure things. On to the rankings. [+] EnlargeKevin C. Cox/Getty ImagesSteve Smith led the Panthers with 982 receiving yards last season.Steve Smith,mlb all star jersey, Panthers. There were three guys among the contest and the other two had better numbers than Smith last annual But Im playing a hunch that Smith will have a monster season,reversible basketball jerseys, even notwithstanding the Panthers have some uncertainty along quarterback. Im basing this aboard my theory that Smith,make your own nfl jersey, always a high-energy companion,vintage nhl jersey,will be extra motivated than ever after simmering on the sidelines throughout training camp meantime reviving from a broken arm. -

San Jose Sharks Vs. Tampa Bay Lightning
San Jose Sharks!! Wednesday, December 21st vs. Tampa Bay Lightning!!! Scouts and Scout Leaders, our fourth Scout Night of the season has already sold out so we would like to offer Dec. 21st as well! vs. Your San Jose Sharks including Joe Thornton, Patrick Marleau and Dan Boyle will take on Steven Stamkos and the Tampa Bay Lightning! So come out and support your San Jose Sharks by taking advantage of this special offer! Exclusive Girls and Boys Scout Offer Wednesday, Dec. 21st @ 7:30 PM! Special discounted ticket to the game, no Ticketmaster fees! Commemorative Scout Patch pictured left! Tickets priced at $55 (red), $45 (tan) and $38 (yellow)**! Save up to $25+ per ticket!!!!! Groups of 25+ get a video board announcement! **For upper reserve sideline and end goalie view seats in the red, tan and yellow sections. Paste the link here into your browser for a seating/pricing map! http://sharks.nhl.com/club/page.htm?id=46597 How many patches will you need? ______ A portion of the proceeds benefit the Girl Scouts of Northern California! These special discounts available for Scouts, their families, & friends. Orders must be paid with VISA, MasterCard, American Express or by check payable to the San Jose Sharks. Your order will be filled with the best available seats at the time your order is processed, and tickets will be placed at Will Call under the name listed below for pick up on the day of the event. Orders must be received by 5:00pm, Friday, December 16th. San Jose Sharks vs. -

Turnbull Hockey Pool For
Turnbull Hockey Pool for Each year, Turnbull students participate in several fundraising initiatives, which we promote as a way to develop a sense of community, leadership and social responsibility within the students. Last year's grade 7 and 8 students put forth a great deal of effort campaigning friends and family members to join Turnbull's annual NHL hockey pool, raising a total of $1750 for a charity of their choice (the United Way). This year's group has decided to run the hockey pool for the benefit of Help Lesotho, an international development organization working in the AIDS-ravaged country of Lesotho in southern Africa. From www.helplesotho.org "Help Lesotho’s programs foster hope and motivation in those who are most in need: orphans, vulnerable children, at-risk youth and grandmothers. Our work targets root causes and community priorities, including literacy, youth leadership training, school twinning, child sponsorship and gender programming. Help Lesotho is an effective, sustainable organization that is working at the grass-roots level to support the next generation of leaders in Lesotho." Your participation in this year's NHL hockey pool is very much appreciated. We believe it will provide students and their friends and families an opportunity to have fun together while giving back to their community by raising awareness and funds for a great cause. Prizes: > Grand Prize awarded to contestant whose team accumulates the most points over the regular NHL season = 10" Samsung Galaxy Tablet > Monthly Prizes awarded to the contestants whose teams accumulate the most points over each designated period (see website) = Two Movie Passes How it Works: > Everyone in the community is welcome to join in on the fun. -

NHL Playoffs PDF.Xlsx
Anaheim Ducks Boston Bruins POS PLAYER GP G A PTS +/- PIM POS PLAYER GP G A PTS +/- PIM F Ryan Getzlaf 74 15 58 73 7 49 F Brad Marchand 80 39 46 85 18 81 F Ryan Kesler 82 22 36 58 8 83 F David Pastrnak 75 34 36 70 11 34 F Corey Perry 82 19 34 53 2 76 F David Krejci 82 23 31 54 -12 26 F Rickard Rakell 71 33 18 51 10 12 F Patrice Bergeron 79 21 32 53 12 24 F Patrick Eaves~ 79 32 19 51 -2 24 D Torey Krug 81 8 43 51 -10 37 F Jakob Silfverberg 79 23 26 49 10 20 F Ryan Spooner 78 11 28 39 -8 14 D Cam Fowler 80 11 28 39 7 20 F David Backes 74 17 21 38 2 69 F Andrew Cogliano 82 16 19 35 11 26 D Zdeno Chara 75 10 19 29 18 59 F Antoine Vermette 72 9 19 28 -7 42 F Dominic Moore 82 11 14 25 2 44 F Nick Ritchie 77 14 14 28 4 62 F Drew Stafford~ 58 8 13 21 6 24 D Sami Vatanen 71 3 21 24 3 30 F Frank Vatrano 44 10 8 18 -3 14 D Hampus Lindholm 66 6 14 20 13 36 F Riley Nash 81 7 10 17 -1 14 D Josh Manson 82 5 12 17 14 82 D Brandon Carlo 82 6 10 16 9 59 F Ondrej Kase 53 5 10 15 -1 18 F Tim Schaller 59 7 7 14 -6 23 D Kevin Bieksa 81 3 11 14 0 63 F Austin Czarnik 49 5 8 13 -10 12 F Logan Shaw 55 3 7 10 3 10 D Kevan Miller 58 3 10 13 1 50 D Shea Theodore 34 2 7 9 -6 28 D Colin Miller 61 6 7 13 0 55 D Korbinian Holzer 32 2 5 7 0 23 D Adam McQuaid 77 2 8 10 4 71 F Chris Wagner 43 6 1 7 2 6 F Matt Beleskey 49 3 5 8 -10 47 D Brandon Montour 27 2 4 6 11 14 F Noel Acciari 29 2 3 5 3 16 D Clayton Stoner 14 1 2 3 0 28 D John-Michael Liles 36 0 5 5 1 4 F Ryan Garbutt 27 2 1 3 -3 20 F Jimmy Hayes 58 2 3 5 -3 29 F Jared Boll 51 0 3 3 -3 87 F Peter Cehlarik 11 0 2 2 -

What Is the Value of an Action in Ice Hockey? Learning a Q-Function for the NHL
What is the Value of an Action in Ice Hockey? Learning a Q-function for the NHL Oliver Schulte, Zeyu Zhao, and Kurt Routley Simon Fraser University, Burnaby, BC, Canada {oschulte}@cs.sfu.ca Abstract. Recent work has applied the Markov Game formalism from AI to model game dynamics for ice hockey, using a large state space. Dy- namic programming is used to learn action-value functions that quantify the impact of actions on goal scoring. Learning is based on a massive dataset that contains over 2.8M events in the National Hockey League. As an application of the Markov model, we use the learned action val- ues to measure the impact of player actions on goal scoring. Players are ranked according to the aggregate goal impact of their actions. We show that this ranking is consistent across across seasons, and compare it with previous player metrics, such as plus-minus and total points. 1 Introduction This paper describes and extends a recent approach to sports analytics that applies advanced concepts from Artificial Intelligence to model game dynamics. This approach models game dynamics using Markov games [4], a multi-agent extension of Markov Decision Processes. A Markov game model can answer a fundamental question about a sport: Which actions contribute to winning in what situation? We approach this question for ice hockey by learning an action-value func- tion, or Q-function, for a Markov game model of the National Hockey League (NHL). In reinforcement learning (RL) notation, the expression Q(s; a) denotes the expected reward of taking action a in state s. -

Forbes Magazine Has Ranked Edge Sports Management As One of the Top Ten Hockey Agencies in the World
Forbes Magazine has ranked Edge Sports Management as one of the top ten hockey agencies in the world. Edge Sports Management is a full service firm dedicated to advising and representing hockey players at every stage of their careers and lives. We have had extensive experience and success in advising players to enhance their draft status. We have also been successful in securing top contracts for players that have gone undrafted. We have negotiated “salary cap” contracts for drafted and undrafted entry level players; been very successful in salary arbitration; have procured excellent contracts for NHL free agents; and negotiated some of the largest contracts in the history of the National Hockey League. No matter what contractual situation a player is in, Edge Sports Management has been there before, and our clients can rely on our experience and expertise to negotiate a successful result. What distinguishes us from most agencies is that we pride ourselves on being personally accessible to players and their families at all times. We realize and embrace the fact that our responsibilities to our clients go far beyond simply negotiating a contract. We are there to help our players and their families at every stage of their lives, and in any situation that they may need assistance. To us, there is nothing more rewarding than helping a client achieve success on the ice, while knowing that he and his family are taken care of in all aspects of life. Who We Are We have over 30 years of experience, and have negotiated hundreds of millions dollars worth of contracts. -
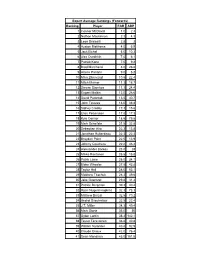
FHN 2021 Draft Guide
Expert Average Rankings (Forwards) Ranking Player EAR ADP 1 Connor McDavid 1.0 2.3 2 Nathan Mackinnon 2.3 4.3 3 Leon Draisaitl 2.8 3 4 Auston Matthews 4.0 6.9 5 Jack Eichel 5.0 10.3 6 Alex Ovechkin 7.0 6.1 7 Patrick Kane 7.0 9.8 8 Brad Marchand 8.0 26.6 9 Artemi Panarin 9.0 5.8 10 Mika Zibanejad 10.8 22.4 11 Mitch Marner 11.3 18.7 12 Steven Stamkos 11.3 24.4 13 Evgeni Malkin 13.0 28.6 14 David Pastrnak 13.5 40.7 15 John Tavares 16.0 33.8 16 Sidney Crosby 17.3 15.6 17 Elias Pettersson 17.8 17.3 18 Kyle Connor 18.5 75.6 19 Mark Scheifele 21.5 32.8 20 Sebastian Aho 22.3 13.8 21 Jonathan Huberdeau 22.3 22.3 22 Brayden Point 22.5 13.9 23 Johnny Gaudreau 22.8 48.2 24 Aleksander Barkov 23.8 28 25 Mikko Rantanen 25.5 15.8 26 Patrik Laine 26.0 34.1 27 Blake Wheeler 27.8 43.8 28 Taylor Hall 28.0 53.1 29 Matthew Tkachuk 28.3 39.6 30 Jake Guentzel 29.8 31.4 31 Patrice Bergeron 30.3 40.4 32 Ryan Nugent-Hopkins 32.3 73.3 33 Mathew Barzal 32.5 70.2 34 Andrei Svechnikov 33.5 22.4 35 J.T. Miller 34.3 49.4 36 Mark Stone 35.0 30 37 Dylan Larkin 38.3 142.1 38 Teuvo Teravainen 38.8 40.8 39 William Nylander 40.8 92.9 40 Claude Giroux 42.0 76.4 41 Sean Monahan 43.0 151.5 42 Max Pacioretty 43.3 46 43 Elias Lindholm 43.8 81.8 44 Filip Forsberg 46.0 77.1 45 Brock Boeser 47.0 51.7 46 Anze Kopitar 48.8 137 47 Travis Konecny 49.3 96.8 48 Sean Couturier 49.5 69.4 49 Kevin Fiala 51.8 82.5 50 Bo Horvat 52.3 141.4 51 Gabriel Landeskog 53.3 38.6 52 Brendan Gallagher 53.5 87.7 53 Evander Kane 54.8 90 54 Ryan O'Reilly 56.0 69.8 55 Anthony Mantha 56.3 153.7 56 Evgeny Dadonov -

Nhl Morning Skate – Nov
NHL MORNING SKATE – NOV. 25, 2018 SATURDAY’S RESULTS Home Team in Caps Washington 5, NY RANGERS 3 TORONTO 6, Philadelphia 0 Boston 3, MONTREAL 2, Buffalo 3, DETROIT 2 (SO) Chicago 5, FLORIDA 4 (OT) NY ISLANDERS 4, Carolina 1 PITTSBURGH 4, Columbus 2 Winnipeg 8, ST. LOUIS 4 COLORADO 3, Dallas 2 VEGAS 6, San Jose 0 Vancouver 4, LOS ANGELES 2 LAINE BREAKS RECORDS WITH FIRST FIVE-GOAL GAME IN NEARLY EIGHT YEARS Patrik Laine became the first NHL player in nearly eight years to score five goals in a game, setting franchise records for most in a game and calendar month to take sole possession of the League lead this season (19). He has scored 16 times since returning to his native Finland for the 2018 NHL Global Series on Nov. 1 - where he scored his first of three hat tricks this month. * Laine tallied the 57th performance of five or more goals in a NHL regular-season game – the 17th by a visiting player - and first since Detroit’s Johan Franzen on Feb. 2, 2011 at OTT. The only other player to score five goals in a game since 1997-98 is Marian Gaborik, on Dec. 20, 2007 vs. NYR. * Laine (20 years, 219 days) is the third different player in League history to score five goals in a game before his 21st birthday, joining Don Murdoch (Oct. 12, 1976: 19 years, 353 days) and Wayne Gretzky, who accomplished the feat twice (Feb. 18, 1981: 20 years, 23 days; and Dec. 30, 1981: 20 years, 338 days). -

CANADA Vs. SLOVAKIA/SLOVAQUIE
Team Canada/ Équipe Canada GAME NOTES/ NOTES DE MATCH CANADA vs. SLOVAKIA/SLOVAQUIE GRAND FORKS, ND December 25, 2004/ 25 Décembre 2004 TEAM CANADA ROSTER ALIGNEMENT D’ÉQUIPE CANADA December 25, 2004/ 25 décembre 2004 CANADA # Goaltenders P S Birthdate Hometown Team League # Gardiens P L Naissance Ville d’origine Équipe Ligue 33 Jeff GLASS G L/G 11/19/85 Cochrane, AB Kootenay WHL 35 Réjean BEAUCHEMIN G L/G 05/03/85 Winnipeg, MB Prince Albert WHL # Players P S Birthdate Hometown Team League # Joueurs P L Naissance Ville d’origine Équipe Ligue 2 **Brent SEABROOK D R/D 04/20/85 Tsawwassen, BC Lethbridge WHL 3 Dion PHANEUF D L/G 04/10/85 Edmonton, AB Red Deer WHL 4 Shawn BELLE D L/G 01/03/85 Edmonton, AB Tri-City WHL 6 Shea WEBER D R/D 08/14/85 Sicamous, BC Kelowna WHL 20 Danny SYVRET D L/G 06/13/85 Millgrove, ON London OHL 25 Cam BARKER D L/G 04/04/86 Winnipeg, MB Medicine Hat WHL 29 Braydon COBURN D L/G 02/27/85 Shaunavon, SK Portland WHL 34 Kyle QUINCEY D L/G 08/12/85 Caledon, ON Mississauga OHL 7 Jeff CARTER F/A R/D 01/01/85 London, ON Sault Ste. Marie OHL 9 Sidney CROSBY F/A L/G 08/07/87 Cole Harbour, NS Rimouski LHJMQ 11 Colin FRASER F/A L/G 01/28/85 Surrey, BC Red Deer WHL 12 Anthony STEWART F/A R/D 01/05/85 Scarborough, ON Kingston OHL 14 Stephen DIXON F/A L/G 09/07/85 Halifax, NS Cape Breton LHJMQ 15 Ryan GETZLAF F/A R/D 05/10/85 Regina, SK Calgary WHL 18 Michael RICHARDS F/A L/G 02/11/85 Kenora, ON Kitchener OHL 17 Clarke MACARTHUR F/A L/G 04/06/85 Lloydminster, AB Medicine Hat WHL 19 Andrew LADD F/A L/G 12/12/85 Maple Ridge, BC -
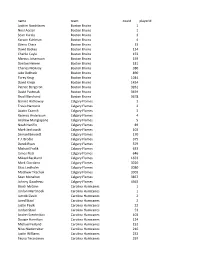
2019 Playoff Draft Player Frequency Report
name team count playerid Joakim Nordstrom Boston Bruins 1 Noel Acciari Boston Bruins 1 Sean Kuraly Boston Bruins 3 Karson Kuhlman Boston Bruins 4 Zdeno Chara Boston Bruins 13 David Backes Boston Bruins 134 Charlie Coyle Boston Bruins 153 Marcus Johansson Boston Bruins 159 Danton Heinen Boston Bruins 181 Charles McAvoy Boston Bruins 380 Jake DeBrusk Boston Bruins 890 Torey Krug Boston Bruins 1044 David Krejci Boston Bruins 1434 Patrice Bergeron Boston Bruins 3261 David Pastrnak Boston Bruins 3459 Brad Marchand Boston Bruins 3678 Garnet Hathaway Calgary Flames 2 Travis Hamonic Calgary Flames 2 Austin Czarnik Calgary Flames 3 Rasmus Andersson Calgary Flames 4 Andrew Mangiapane Calgary Flames 5 Noah Hanifin Calgary Flames 89 Mark Jankowski Calgary Flames 102 Samuel Bennett Calgary Flames 170 T.J. Brodie Calgary Flames 375 Derek Ryan Calgary Flames 379 Michael Frolik Calgary Flames 633 James Neal Calgary Flames 646 Mikael Backlund Calgary Flames 1653 Mark Giordano Calgary Flames 3020 Elias Lindholm Calgary Flames 3080 Matthew Tkachuk Calgary Flames 3303 Sean Monahan Calgary Flames 3857 Johnny Gaudreau Calgary Flames 4363 Brock McGinn Carolina Hurricanes 1 Jordan Martinook Carolina Hurricanes 1 Jaccob Slavin Carolina Hurricanes 2 Jared Staal Carolina Hurricanes 2 Justin Faulk Carolina Hurricanes 22 Jordan Staal Carolina Hurricanes 53 Andrei Svechnikov Carolina Hurricanes 103 Dougie Hamilton Carolina Hurricanes 124 Michael Ferland Carolina Hurricanes 152 Nino Niederreiter Carolina Hurricanes 216 Justin Williams Carolina Hurricanes 232 Teuvo Teravainen Carolina Hurricanes 297 Sebastian Aho Carolina Hurricanes 419 Nikita Zadorov Colorado Avalanche 1 Samuel Girard Colorado Avalanche 1 Matthew Nieto Colorado Avalanche 1 Cale Makar Colorado Avalanche 2 Erik Johnson Colorado Avalanche 2 Tyson Jost Colorado Avalanche 3 Josh Anderson Colorado Avalanche 14 Colin Wilson Colorado Avalanche 14 Matt Calvert Colorado Avalanche 14 Derick Brassard Colorado Avalanche 28 J.T.