DOCSLIB.ORG

Thermal Property Prediction and Measurement of Organic Phase Change Materials in the Liquid Phase Near the Melting Point Q ⇑ William E

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Thermal Property Prediction and Measurement of Organic Phase Change Materials in the Liquid Phase Near the Melting Point Q ⇑ William E Applied Energy 132 (2014) 496–506 Contents lists available at ScienceDirect Applied Energy journal homepage: www.elsevier.com/locate/apenergy Thermal property prediction and measurement of organic phase change materials in the liquid phase near the melting point q ⇑ William E. O’Connor, Ronald Warzoha, Rebecca Weigand, Amy S. Fleischer, Aaron P. Wemhoff Department of Mechanical Engineering, Villanova University, 800 Lancaster Ave., Villanova, PA 19085, USA highlights Liquid-phase thermal properties for five phase change materials were estimated. Various liquid phase and phase transition thermal properties were measured. The thermal diffusivity was found using a best path to prediction approach. The thermal diffusivity predictive method shows 15% agreement for organic PCMs. article info abstract Article history: Organic phase change materials (PCMs) are a popular choice for many thermal energy storage applica- Received 20 February 2014 tions including solar energy, building envelope thermal barriers, and passive cooling of portable electron- Received in revised form 18 June 2014 ics. Since the extent of phase change during a heating or cooling process is dependent upon rapid thermal Accepted 11 July 2014 penetration into the PCM, accurate knowledge of the thermal diffusivity of the PCM in both solid and liquid phases is crucial. This study addresses the existing gaps in information for liquid-phase PCM properties by examining an approach that determines the best path to prediction (BPP) for the thermal Keywords: diffusivity of both alkanes and unsaturated acids. Knowledge of the BPP will enable researchers to explore Phase change material the influence of PCM molecular structure on bulk thermophysical properties, thereby allowing the Statistical thermodynamics Thermophysical properties fabrication of optimized PCMs. Differential scanning calorimetry The BPP method determines which of the tens of thousands of combinations of 22 different available Transient plane source theoretical techniques provides best agreement with thermal diffusivity values based on reported or Thermal diffusivity measured density, heat capacity, and thermal conductivity for each of five PCMs (heneicosane, tricosane, tetracosane, oleic acid, and linoleic acid) in the liquid phase near the melting point. Separate BPPs were calibrated for alkanes based on heneicosane and tetracosane, and for the unsaturated acids. The alkane and unsaturated acid BPPs were then tested on a variety of similar materials, showing agreement with reported/measured thermal diffusivity within 15% for all materials. The alkane BPP was then applied to find that increasing the length of alkane chains decreases the PCM thermal diffusivity, showing how the determination of the BPP can be used to aid in the prediction of how the molecular structure of organic PCMs influences PCM performance in energy storage applications. Ó 2014 Elsevier Ltd. All rights reserved. 1. Introduction electronics [17–19]. Since the extent of phase change during a heating or cooling process is dependent upon the amount of ther- Organic phase change materials (PCMs) have been proposed as mal penetration into the PCM, the thermal diffusivity of the PCM is a viable energy storage mechanism through solid–liquid phase an important thermophysical property for the viability of the change at the melting point temperature. This energy storage could material in an energy storage application. have significant applications in solar energy [1–7], building The thermal diffusivity, ath, is defined as envelope thermal barriers [8–16], and passive cooling of portable k ath ¼ ð1Þ qcp q Submitted for consideration for publication in Applied Energy. ⇑ Corresponding author. Fax: +1 610 519 7312. where k is thermal conductivity, q is mass density, and cP is the E-mail address: [email protected] (A.P. Wemhoff). mass-based heat capacity. Data regarding some of the solid and http://dx.doi.org/10.1016/j.apenergy.2014.07.045 0306-2619/Ó 2014 Elsevier Ltd. All rights reserved. W.E. O’Connor et al. / Applied Energy 132 (2014) 496–506 497 Nomenclature ai, di group contribution parameters, dimensionless tck critical temperature group contribution parameter, aP Peng–Robinson fluid model intermolecular potential dimensionless parameter, J m3 tfp1k first-order melting temperature group contribution aR Redlich–Kwong fluid model intermolecular potential parameter, dimensionless parameter, J m3 K0.5 tfp2j second-order melting temperature group contribution aS Soave–Redlich–Kwong fluid model intermolecular parameter, dimensionless potential parameter, J m3 P pressure, Pa aV Van der Waals fluid model intermolecular potential Pc critical pressure, Pa 3 parameter, J m Po atmospheric pressure, Pa bP Peng–Robinson fluid model equivalent molecular Pr reduced pressure, dimensionless 3 volume, m Prb reduced boiling point pressure, dimensionless bR Redlich–Kwong fluid model equivalent molecular Q canonical partition function, dimensionless volume, m3 R ideal gas constant, J/(kmol K) bS Soave–Redlich–Kwong fluid model equivalent molecu- T temperature, K 3 lar volume, m Tb boiling point temperature, K bV Van der Waals fluid model equivalent molecular Tc critical temperature, K 3 volume, m Tm melting point temperature, K cp mass-based heat capacity, J/(kg K) Trb reduced boiling point temperature, dimensionless Cpl molar heat capacity, J/(mol K) U system internal energy, J 3 cp,st mass-based heat capacity of sapphire sample, J/(kg K) Vs saturated liquid molar volume, cm /mol Ds difference in heat flow between empty reference pan W weight for second-order groups (= 0 for 1st order, = 1 for and sample of interest, mW 2nd order), dimensionless Dst difference in heat flow between empty reference pan Ws weight of sample of interest, mg and sapphire sample, mW Wst weight of sapphire sample, mg E reference calorimetric sensitivity, dimensionless Z critical compressibility factor, dimensionless 2 f,a fluid model-dependent parameters, dimensionless ath thermal diffusivity, m /s g temperature ramp rate, °C/min DHf latent heat of fusion, J/kg H system enthalpy, J DHm total enthalpy of melting, J/mol h Planck’s constant, J s DSm total entropy of melting, J/(mol K) kB Boltzmann’s constant, J/K e molecular eccentricity, dimensionless M molecular mass, kg/kmol hrot,m rotational temperature, K mi melting enthalpy group contribution parameter, dimen- k thermal conductivity, W/(m K) à sionless kf reduced thermal conductivity correction term, dimen- Mj occurrence of group j in a molecule, dimensionless sionless à N number of molecules in a system, dimensionless km reduced thermal conductivity of a monatomic liquid, Natoms number of atoms, dimensionless dimensionless À1 NA Avogadro’s number, kmol n number of molecular degrees of freedom, dimensionless 3 ni occurrence of group i in a molecule, dimensionless q mass density, kg/m Nk occurrence of group k in a molecule, dimensionless r molecular symmetry, dimensionless pck critical pressure group contribution parameter, dimen- s molecular flexibility, dimensionless sionless x acentric factor, dimensionless liquid phase properties of organic PCMs on the right-hand side of equivalent in numerical investigations [10,12,22]. Therefore, this Eq. (1) are readily available [20,21], but gaps exist in available data. study aims at determining accurate predictive techniques of liquid Furthermore, the gaps in liquid-phase properties cannot be filled by phase thermophysical properties for two principal classes of equivalent solid phase properties since the shifted molecular organic PCMs: alkanes and unsaturated (fatty) acids. arrangement between solid and liquid phases could have a dramatic This study is intended to supplement the large body of work on influence on the thermophysical properties in the following ways PCM enhancement using nanoscale inclusions. Several studies through a loss of a molecular lattice structure: [23–27] investigated the impact of adding highly-conducting The lattice configuration contains a strong influence on the scat- nanoscale inclusions into a base organic PCM. In general, research- tering mechanisms in phonon behavior in thermal conduction. ers have found that these composites contain significant conduc- Losing the lattice structure adjusts the available effective tivity enhancement (in general >100% enhancement for >1 wt% degrees of freedom of the molecules, thereby altering the spe- filler) but with a sacrifice in the latent enthalpy of fusion (7– cific heat. 15% reduction for typical loading values). Fan et al. [26] compared A loss in lattice structure affects the molecular packing arrange- different fillers and found that graphene nanoplatelets and short ment, influencing the material density. cylindrical inclusions (e.g., carbon nanotubes) provide better con- ductivity enhancement than long inclusions. The limiting factor Furthermore, a PCM ideally exists in its liquid phase during one in PCM nano-composite performance is the combination of ther- half of a heating/cooling cycle, and therefore an accurate model of mal properties associated with the base PCM, and therefore the thermal response of the PCM should apply the liquid phase improving the thermal properties of the base PCM – the focus of thermal properties, especially during a freezing process. However, this effort – will lead to more effective PCM nano-composites. many investigators have either ignored thermal gradients within A number of theoretical techniques exist to determine various the PCM [9] or assumed that the solid and liquid properties are properties
Load more

Recommended publications
  • Catalytic Pyrolysis of Plastic Wastes for the Production of Liquid Fuels for Engines
    Electronic Supplementary Material (ESI) for RSC Advances. This journal is © The Royal Society of Chemistry 2019 Supporting information for: Catalytic pyrolysis of plastic wastes for the production of liquid fuels for engines Supattra Budsaereechaia, Andrew J. Huntb and Yuvarat Ngernyen*a aDepartment of Chemical Engineering, Faculty of Engineering, Khon Kaen University, Khon Kaen, 40002, Thailand. E-mail:[email protected] bMaterials Chemistry Research Center, Department of Chemistry and Center of Excellence for Innovation in Chemistry, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand Fig. S1 The process for pelletization of catalyst PS PS+bentonite PP ) t e PP+bentonite s f f o % ( LDPE e c n a t t LDPE+bentonite s i m s n HDPE a r T HDPE+bentonite Gasohol 91 Diesel 4000 3500 3000 2500 2000 1500 1000 500 Wavenumber (cm-1) Fig. S2 FTIR spectra of oil from pyrolysis of plastic waste type. Table S1 Compounds in oils (%Area) from the pyrolysis of plastic wastes as detected by GCMS analysis PS PP LDPE HDPE Gasohol 91 Diesel Compound NC C Compound NC C Compound NC C Compound NC C 1- 0 0.15 Pentane 1.13 1.29 n-Hexane 0.71 0.73 n-Hexane 0.65 0.64 Butane, 2- Octane : 0.32 Tetradecene methyl- : 2.60 Toluene 7.93 7.56 Cyclohexane 2.28 2.51 1-Hexene 1.05 1.10 1-Hexene 1.15 1.16 Pentane : 1.95 Nonane : 0.83 Ethylbenzen 15.07 11.29 Heptane, 4- 1.81 1.68 Heptane 1.26 1.35 Heptane 1.22 1.23 Butane, 2,2- Decane : 1.34 e methyl- dimethyl- : 0.47 1-Tridecene 0 0.14 2,2-Dimethyl- 0.63 0 1-Heptene 1.37 1.46 1-Heptene 1.32 1.35 Pentane,
    [Show full text]
  • Synthetic Turf Scientific Advisory Panel Meeting Materials
    California Environmental Protection Agency Office of Environmental Health Hazard Assessment Synthetic Turf Study Synthetic Turf Scientific Advisory Panel Meeting May 31, 2019 MEETING MATERIALS THIS PAGE LEFT BLANK INTENTIONALLY Office of Environmental Health Hazard Assessment California Environmental Protection Agency Agenda Synthetic Turf Scientific Advisory Panel Meeting May 31, 2019, 9:30 a.m. – 4:00 p.m. 1001 I Street, CalEPA Headquarters Building, Sacramento Byron Sher Auditorium The agenda for this meeting is given below. The order of items on the agenda is provided for general reference only. The order in which items are taken up by the Panel is subject to change. 1. Welcome and Opening Remarks 2. Synthetic Turf and Playground Studies Overview 4. Synthetic Turf Field Exposure Model Exposure Equations Exposure Parameters 3. Non-Targeted Chemical Analysis Volatile Organics on Synthetic Turf Fields Non-Polar Organics Constituents in Crumb Rubber Polar Organic Constituents in Crumb Rubber 5. Public Comments: For members of the public attending in-person: Comments will be limited to three minutes per commenter. For members of the public attending via the internet: Comments may be sent via email to [email protected]. Email comments will be read aloud, up to three minutes each, by staff of OEHHA during the public comment period, as time allows. 6. Further Panel Discussion and Closing Remarks 7. Wrap Up and Adjournment Agenda Synthetic Turf Advisory Panel Meeting May 31, 2019 THIS PAGE LEFT BLANK INTENTIONALLY Office of Environmental Health Hazard Assessment California Environmental Protection Agency DRAFT for Discussion at May 2019 SAP Meeting. Table of Contents Synthetic Turf and Playground Studies Overview May 2019 Update .....
    [Show full text]
  • The Enthalpy of Formation of Organic Compounds with “Chemical Accuracy”
    chemengineering Article Group Contribution Revisited: The Enthalpy of Formation of Organic Compounds with “Chemical Accuracy” Robert J. Meier Pro-Deo Consultant, 52525 Heinsberg, North-Rhine Westphalia, Germany; [email protected] Abstract: Group contribution (GC) methods to predict thermochemical properties are of eminent importance to process design. Compared to previous works, we present an improved group contri- bution parametrization for the heat of formation of organic molecules exhibiting chemical accuracy, i.e., a maximum 1 kcal/mol (4.2 kJ/mol) difference between the experiment and model, while, at the same time, minimizing the number of parameters. The latter is extremely important as too many parameters lead to overfitting and, therewith, to more or less serious incorrect predictions for molecules that were not within the data set used for parametrization. Moreover, it was found to be important to explicitly account for common chemical knowledge, e.g., geminal effects or ring strain. The group-related parameters were determined step-wise: first, alkanes only, and then only one additional group in the next class of molecules. This ensures unique and optimal parameter values for each chemical group. All data will be made available, enabling other researchers to extend the set to other classes of molecules. Keywords: enthalpy of formation; thermodynamics; molecular modeling; group contribution method; quantum mechanical method; chemical accuracy; process design Citation: Meier, R.J. Group Contribution Revisited: The Enthalpy of Formation of Organic Compounds with “Chemical Accuracy”. 1. Introduction ChemEngineering 2021, 5, 24. To understand chemical reactivity and/or chemical equilibria, knowledge of thermo- o https://doi.org/10.3390/ dynamic properties such as gas-phase standard enthalpy of formation DfH gas is a necessity.
    [Show full text]
  • Measurements of Higher Alkanes Using NO Chemical Ionization in PTR-Tof-MS
    Atmos. Chem. Phys., 20, 14123–14138, 2020 https://doi.org/10.5194/acp-20-14123-2020 © Author(s) 2020. This work is distributed under the Creative Commons Attribution 4.0 License. Measurements of higher alkanes using NOC chemical ionization in PTR-ToF-MS: important contributions of higher alkanes to secondary organic aerosols in China Chaomin Wang1,2, Bin Yuan1,2, Caihong Wu1,2, Sihang Wang1,2, Jipeng Qi1,2, Baolin Wang3, Zelong Wang1,2, Weiwei Hu4, Wei Chen4, Chenshuo Ye5, Wenjie Wang5, Yele Sun6, Chen Wang3, Shan Huang1,2, Wei Song4, Xinming Wang4, Suxia Yang1,2, Shenyang Zhang1,2, Wanyun Xu7, Nan Ma1,2, Zhanyi Zhang1,2, Bin Jiang1,2, Hang Su8, Yafang Cheng8, Xuemei Wang1,2, and Min Shao1,2 1Institute for Environmental and Climate Research, Jinan University, 511443 Guangzhou, China 2Guangdong-Hongkong-Macau Joint Laboratory of Collaborative Innovation for Environmental Quality, 511443 Guangzhou, China 3School of Environmental Science and Engineering, Qilu University of Technology (Shandong Academy of Sciences), 250353 Jinan, China 4State Key Laboratory of Organic Geochemistry and Guangdong Key Laboratory of Environmental Protection and Resources Utilization, Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, 510640 Guangzhou, China 5State Joint Key Laboratory of Environmental Simulation and Pollution Control, College of Environmental Sciences and Engineering, Peking University, 100871 Beijing, China 6State Key Laboratory of Atmospheric Boundary Physics and Atmospheric Chemistry, Institute of Atmospheric Physics, Chinese
    [Show full text]
  • Supporting Information for Modeling the Formation and Composition Of
    Supporting Information for Modeling the Formation and Composition of Secondary Organic Aerosol from Diesel Exhaust Using Parameterized and Semi-explicit Chemistry and Thermodynamic Models Sailaja Eluri1, Christopher D. Cappa2, Beth Friedman3, Delphine K. Farmer3, and Shantanu H. Jathar1 1 Department of Mechanical Engineering, Colorado State University, Fort Collins, CO, USA, 80523 2 Department of Civil and Environmental Engineering, University of California Davis, Davis, CA, USA, 95616 3 Department of Chemistry, Colorado State University, Fort Collins, CO, USA, 80523 Correspondence to: Shantanu H. Jathar ([email protected]) Table S1: Mass speciation and kOH for VOC emissions profile #3161 3 -1 - Species Name kOH (cm molecules s Mass Percent (%) 1) (1-methylpropyl) benzene 8.50×10'() 0.023 (2-methylpropyl) benzene 8.71×10'() 0.060 1,2,3-trimethylbenzene 3.27×10'(( 0.056 1,2,4-trimethylbenzene 3.25×10'(( 0.246 1,2-diethylbenzene 8.11×10'() 0.042 1,2-propadiene 9.82×10'() 0.218 1,3,5-trimethylbenzene 5.67×10'(( 0.088 1,3-butadiene 6.66×10'(( 0.088 1-butene 3.14×10'(( 0.311 1-methyl-2-ethylbenzene 7.44×10'() 0.065 1-methyl-3-ethylbenzene 1.39×10'(( 0.116 1-pentene 3.14×10'(( 0.148 2,2,4-trimethylpentane 3.34×10'() 0.139 2,2-dimethylbutane 2.23×10'() 0.028 2,3,4-trimethylpentane 6.60×10'() 0.009 2,3-dimethyl-1-butene 5.38×10'(( 0.014 2,3-dimethylhexane 8.55×10'() 0.005 2,3-dimethylpentane 7.14×10'() 0.032 2,4-dimethylhexane 8.55×10'() 0.019 2,4-dimethylpentane 4.77×10'() 0.009 2-methylheptane 8.28×10'() 0.028 2-methylhexane 6.86×10'()
    [Show full text]
  • Vapor Pressures and Vaporization Enthalpies of the N-Alkanes from 2 C21 to C30 at T ) 298.15 K by Correlation Gas Chromatography
    BATCH: je1a04 USER: jeh69 DIV: @xyv04/data1/CLS_pj/GRP_je/JOB_i01/DIV_je0301747 DATE: October 17, 2003 1 Vapor Pressures and Vaporization Enthalpies of the n-Alkanes from 2 C21 to C30 at T ) 298.15 K by Correlation Gas Chromatography 3 James S. Chickos* and William Hanshaw 4 Department of Chemistry and Biochemistry, University of MissourisSt. Louis, St. Louis, Missouri 63121 5 6 The temperature dependence of gas chromatographic retention times for n-heptadecane to n-triacontane 7 is reported. These data are used to evaluate the vaporization enthalpies of these compounds at T ) 298.15 8 K, and a protocol is described that provides vapor pressures of these n-alkanes from T ) 298.15 to 575 9 K. The vapor pressure and vaporization enthalpy results obtained are compared with existing literature 10 data where possible and found to be internally consistent. Sublimation enthalpies for n-C17 to n-C30 are 11 calculated by combining vaporization enthalpies with fusion enthalpies and are compared when possible 12 to direct measurements. 13 14 Introduction 15 The n-alkanes serve as excellent standards for the 16 measurement of vaporization enthalpies of hydrocarbons.1,2 17 Recently, the vaporization enthalpies of the n-alkanes 18 reported in the literature were examined and experimental 19 values were selected on the basis of how well their 20 vaporization enthalpies correlated with their enthalpies of 21 transfer from solution to the gas phase as measured by gas 22 chromatography.3 A plot of the vaporization enthalpies of 23 the n-alkanes as a function of the number of carbon atoms 24 is given in Figure 1.
    [Show full text]
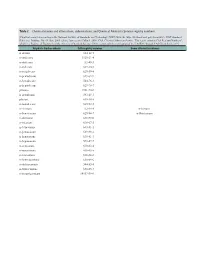
  • Table 2. Chemical Names and Alternatives, Abbreviations, and Chemical Abstracts Service Registry Numbers
    Table 2. Chemical names and alternatives, abbreviations, and Chemical Abstracts Service registry numbers. [Final list compiled according to the National Institute of Standards and Technology (NIST) Web site (http://webbook.nist.gov/chemistry/); NIST Standard Reference Database No. 69, June 2005 release, last accessed May 9, 2008. CAS, Chemical Abstracts Service. This report contains CAS Registry Numbers®, which is a Registered Trademark of the American Chemical Society. CAS recommends the verification of the CASRNs through CAS Client ServicesSM] Aliphatic hydrocarbons CAS registry number Some alternative names n-decane 124-18-5 n-undecane 1120-21-4 n-dodecane 112-40-3 n-tridecane 629-50-5 n-tetradecane 629-59-4 n-pentadecane 629-62-9 n-hexadecane 544-76-3 n-heptadecane 629-78-7 pristane 1921-70-6 n-octadecane 593-45-3 phytane 638-36-8 n-nonadecane 629-92-5 n-eicosane 112-95-8 n-Icosane n-heneicosane 629-94-7 n-Henicosane n-docosane 629-97-0 n-tricosane 638-67-5 n-tetracosane 643-31-1 n-pentacosane 629-99-2 n-hexacosane 630-01-3 n-heptacosane 593-49-7 n-octacosane 630-02-4 n-nonacosane 630-03-5 n-triacontane 638-68-6 n-hentriacontane 630-04-6 n-dotriacontane 544-85-4 n-tritriacontane 630-05-7 n-tetratriacontane 14167-59-0 Table 2. Chemical names and alternatives, abbreviations, and Chemical Abstracts Service registry numbers.—Continued [Final list compiled according to the National Institute of Standards and Technology (NIST) Web site (http://webbook.nist.gov/chemistry/); NIST Standard Reference Database No.
    [Show full text]
  • Thermodynamic Modelling of Hydrocarbon-Chains and Light-Weight Supercritical Solvents
    Thermodynamic modelling of hydrocarbon-chains and light-weight supercritical solvents by James Edward Lombard Thesis presented in partial fulfilment of the requirements for the Degree of MASTER OF ENGINEERING (CHEMICAL ENGINEERING) in the Faculty of Engineering at Stellenbosch University Supervisor Prof. J.H. Knoetze Co-Supervisor/s Dr. C.E. Schwarz March 2015 Stellenbosch University https://scholar.sun.ac.za DECLARATION By submitting this thesis electronically, I declare that the entirety of the work contained therein is my own, original work, that I am the sole author thereof (save to the extent explicitly otherwise stated), that reproduction and publication thereof by Stellenbosch University will not infringe any third party rights and that I have not previously in its entirety or in part submitted it for obtaining any qualification. James Lombard February 2015 ………………………. ………………………. Signature Date Copyright © 2015 Stellenbosch University All rights reserved i Stellenbosch University https://scholar.sun.ac.za ABSTRACT Long-chain hydrocarbons are of value to numerous lucrative industries. Due to the low volatility and close melting and boiling points of these solutes, traditional fractionation methods lack the required selectivity for separation and cause thermal degradation of the product. This project investigates the feasibility of Supercritical Fluid Extraction (SFE) for processing these systems, with the primary objective of modelling the high-pressure vapour-liquid equilibrium (VLE) properties of hydrocarbon solutes with a light-weight solvent using a semi- empirical equation of state (EOS). Pure component vapour pressures and saturated liquid volumes are also investigated. A thorough investigation into the phase behaviour of the n-alkanes, 1-alcohols, carboxylic acids and esters in light weight supercritical solvents CO2, ethane and propane revealed that the solute structure and temperature largely influence the solute solubility and process feasibility.
    [Show full text]
  • Journal of Pharmaceutical and Pharmacological Sciences Samuel P, Et Al., J Pharma Pharma Sci: JPPS-138
    Journal of Pharmaceutical and Pharmacological Sciences Samuel P, et al., J Pharma Pharma Sci: JPPS-138. Research Article DOI:10.29011/2574-7711/100038 Bioprospecting of Salicornia europaeaL. a Marine Halophyte and Evaluation of Its Biological Potential with Special Refer- ence to Anticancer Activity Samuel P1*, Vijaya J Kumar1, Deena R Dhayalan1, Amirtharaj K1, Sudarmani DNP2 1Department of Biotechnology, Ayya Nadar Janaki Ammal College(Autonomous), Sivakasi, TN, India 2Department of Zoology (PG), Ayya Nadar Janaki Ammal College (Autonomous), Sivakasi, TN, India *Corresponding author: Samuel P, Assistant Professor, Department of Biotechnology, Ayya Nadar Janaki Ammal College (Autono- mous), Sivakasi, TN, India. Tel: +919025559994; Email: [email protected] Citation: Samuel P, Kumar VJ, Dhayalan DR, Amirtharaj K, Sudarmani DNP (2017) Bioprospecting of Salicornia europaea L. a Marine Halophyte and Evaluation of Its Biological Potential with Special Reference to Anticancer Activity. J Pharma Pharma Sci: JPPS-138. DOI:10.29011/2574-7711/100038 Received Date: 02 August, 2017; Accepted Date: 25 August, 2017; Published Date: 02 September, 2017 Abstract The present study was initiated with an intention to bring outthe phytochemical profile of the marine halophyte Salicornia europaeaL., the chemical finger print of the halophyte was made by GC-MS.The phytochemicalsin the crude extract was evalu- ated for cytotoxic study against MCF7. The marine halophytes were collected, washedand chopped in to 5cm long and shade dried for 20-25 days in a dark room. The dried and grounded plant materials were subjected to Soxhlet extraction.Two solvents vizmethanol and ethyl acetate were used to prepare decoction of the plant.The extracts were screened using GC-MS and dried us- ing rotary vacuum evaporator.
    [Show full text]
  • ABSTRACT RUDD, HAYDEN. Assessing the Vulnerability Of
    ABSTRACT RUDD, HAYDEN. Assessing the Vulnerability of Coastal Plain Groundwater to Flood Water Intrusion using High Resolution Mass Spectrometry. (Under the direction of Dr. Elizabeth Guthrie Nichols). Communities in the North Carolina Coastal Plain (NCCP) depend on safe and reliable groundwater for private well use, agriculture, industry, and livelihoods. Although storm intensity and frequency are predicted to increase in coastal areas, the risk of surficial and confined aquifer contamination from extreme storms is not understood. In September 2018, Hurricane Florence caused extensive flooding across the NCCP for several weeks. The North Carolina Department of Environmental Quality (NCDEQ) Groundwater Management Branch had just completed sampling of some wells in their monitoring network when Hurricane Florence made landfall. NCDEQ returned to these wells, particularly those flooded by Hurricane Florence, for post-flood sampling. These groundwater samples were analyzed by NCDEQ for regulated semi-volatile organics with few to any detections of regulated organic contaminants. NCDEQ provided NC State the same sample extracts for analysis by high resolution mass spectrometry (HRMS). This research reports on the non-targeted and suspect-screening HRMS analyses of groundwater from nested monitoring wells. Some monitoring well sites experienced flooding during the study period, and some did not. The goal of this research was to advance our understanding of coastal aquifer susceptibility to flooding by producing the first comprehensive organic chemical profiles of coastal aquifers and by determining if aquifers have distinct organic chemical profiles that change after flooding events. This study used HRMS analyses to produce the first comprehensive organic chemical profiles of 11 aquifers in the coastal plain.
    [Show full text]
  • Characteristic List (PDF)
    State of Alaska, Environmental Conservation Water Info Mgt 907-465-5153 Substance/Characteristic Name EPA Substance Registry ID (-)-cis-Permethrin 963314 (-)-trans-Permethrin 963322 (3-Bromopropyl)benzene 65862 2-Chloro-1-phenylethanol 961524 .alpha.,.alpha.-Dimethylphenethylamine 32128 .alpha.-Chlordene 694141 .alpha.-Endosulfan 75333 .alpha.-Hexachlorocyclohexane 42184 .alpha.-Methylstyrene 18317 .alpha.-Nitrotoluene 961201 .alpha.-Terpineol 18127 .beta.-Chlordene 694158 .beta.-Endosulfan 263996 .beta.-Hexachlorocyclohexane 42192 .delta.-Hexachlorocyclohexane 42200 .gamma.-Butyrolactone 16873 .gamma.-Chlordene 694174 Acetovanillone 48074 1,1,1,2-Tetrachloroethane 65102 1,1,1-Trichloro-2-propanone 650242 1,1,1-Trichloroethane 4796 CFC-113a 43570 1,1,2,2-Tetrabromoethane 7716 1,1,2,2-Tetrachloroethane 7773 1,1,2-Trichloroethane 7518 1,1'-Binaphthalene 58701 1,1-Dichloroethane 5520 1,1-Dichloroethylene 5538 1,1-Dichloropropane 7500 1,1-Dichloropropanone 650184 1,1-Dichloropropene 54676 1,1-Dimethylcyclopropane 961516 1,1'-Oxybis[3-chloropropane] 64733 1,2,3,4,5,6-Hexachlorocyclohexane 59220 1,2,3,4,6,7,8,9-Octachlorodibenzofuran 278218 1,2,3,4,6,7,8,9-Octachlorodibenzo-p-dioxin 113837 1,2,3,4,6,7,8-Heptachlorodibenzofuran 358382 1,2,3,4,6,7,8-Heptachlorodibenzo-p-dioxin 270140 1,2,3,4,7,8,9-Heptachlorodibenzofuran 304782 1,2,3,4,7,8-Hexachlorodibenzofuran 525212 1,2,3,4,7,8-Hexachlorodibenzo-p-dioxin 711986 1,2,3,4-Tetrachlorobenzene 65441 1,2,3,4-Tetrahydronaphthalene 30783 1,2,3,4-Tetramethylbenzene 47365 1,2,3,5-Tetrachlorobenzene 65458
    [Show full text]
  • Plasma Assisted Decomposition of Methane and Propane and Cracking of Liquid Hexadecane
    PLASMA ASSISTED DECOMPOSITION OF METHANE AND PROPANE AND CRACKING OF LIQUID HEXADECANE A thesis submitted for the degree of Doctor of Philosophy by Irma Aleknaviciute School of Engineering and Design Brunel University, Uxbridge April, 2013 Abstract Non-thermal plasmas are considered to be very promising for the initiation of chemical reactions and a vast amount of experimental work has been dedicated to plasma assisted hydrocarbon conversion processes, which are reviewed in the fourth chapter of the thesis. However, current knowledge and experimental data available in the literature on plasma assisted liquid hydrocarbon cracking and gaseous hydrocarbon decomposition is very limited. The experimental methodology is introduced in the chapter that follows the literature review. It includes the scope and objectives section reflecting the information presented in the literature review and the rationale of this work. This is followed by a thorough description of the design and construction of the experimental plasma reformer and the precise experimental procedures, the set-up of hydrocarbon characterization equipment and the development of analytical methods. The methodology of uncertainty analysis is also described. In this work we performed experiments in attempt the cracking of liquid hexadecane into smaller liquid hydrocarbons, which was not successful. The conditions tested and the problems encountered are described in detail. In this project we performed a parametric study for methane and propane decomposition under a corona discharge for CO x free hydrogen generation. For methane and propane a series of experiments were performed for a positive corona discharge at a fixed inter-electrode distance (15 mm) to study the effects of discharge power (range of 14 - 20 W and 19 – 35 W respectively) and residence time (60 - 240 s and 60 – 303 s respectively).
    [Show full text]