Hybridization of Sampling-Based Motion Planning Algorithms and Spherical Representations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lecture 04 Linear Structures Sort
Algorithmics (6EAP) MTAT.03.238 Linear structures, sorting, searching, etc Jaak Vilo 2018 Fall Jaak Vilo 1 Big-Oh notation classes Class Informal Intuition Analogy f(n) ∈ ο ( g(n) ) f is dominated by g Strictly below < f(n) ∈ O( g(n) ) Bounded from above Upper bound ≤ f(n) ∈ Θ( g(n) ) Bounded from “equal to” = above and below f(n) ∈ Ω( g(n) ) Bounded from below Lower bound ≥ f(n) ∈ ω( g(n) ) f dominates g Strictly above > Conclusions • Algorithm complexity deals with the behavior in the long-term – worst case -- typical – average case -- quite hard – best case -- bogus, cheating • In practice, long-term sometimes not necessary – E.g. for sorting 20 elements, you dont need fancy algorithms… Linear, sequential, ordered, list … Memory, disk, tape etc – is an ordered sequentially addressed media. Physical ordered list ~ array • Memory /address/ – Garbage collection • Files (character/byte list/lines in text file,…) • Disk – Disk fragmentation Linear data structures: Arrays • Array • Hashed array tree • Bidirectional map • Heightmap • Bit array • Lookup table • Bit field • Matrix • Bitboard • Parallel array • Bitmap • Sorted array • Circular buffer • Sparse array • Control table • Sparse matrix • Image • Iliffe vector • Dynamic array • Variable-length array • Gap buffer Linear data structures: Lists • Doubly linked list • Array list • Xor linked list • Linked list • Zipper • Self-organizing list • Doubly connected edge • Skip list list • Unrolled linked list • Difference list • VList Lists: Array 0 1 size MAX_SIZE-1 3 6 7 5 2 L = int[MAX_SIZE] -

The Algorithms and Data Structures Course Multicomponent Complexity and Interdisciplinary Connections
Technium Vol. 2, Issue 5 pp.161-171 (2020) ISSN: 2668-778X www.techniumscience.com The Algorithms and Data Structures course multicomponent complexity and interdisciplinary connections Gregory Korotenko Dnipro University of Technology, Ukraine [email protected] Leonid Korotenko Dnipro University of Technology, Ukraine [email protected] Abstract. The experience of modern education shows that the trajectory of preparing students is extremely important for their further adaptation in the structure of widespread digitalization, digital transformations and the accumulation of experience with digital platforms of business and production. At the same time, there continue to be reports of a constant (catastrophic) lack of personnel in this area. The basis of the competencies of specialists in the field of computing is the ability to solve algorithmic problems that they have not been encountered before. Therefore, this paper proposes to consider the features of teaching the course Algorithms and Data Structures and possible ways to reduce the level of complexity in its study. Keywords. learning, algorithms, data structures, data processing, programming, mathematics, interdisciplinarity. 1. Introduction The analysis of electronic resources and literary sources allows for the conclusion that the Algorithms and Data Structures course is one of the cornerstones for the study programs related to computing. Moreover, this can be considered not only from the point of view of entering the profession, but also from the point of view of preparation for an interview in hiring as a programmer, including at a large IT organization (Google, Microsoft, Apple, Amazon, etc.) or for a promising startup [1]. As a rule, this course is characterized by an abundance of complex data structures and various algorithms for their processing. -
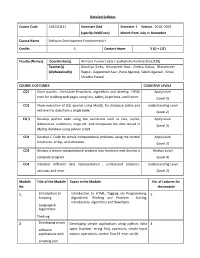
Detailed Syllabus Course Code 15B11CI111 Semester
Detailed Syllabus Course Code 15B11CI111 Semester Odd Semester I. Session 2018 -2019 (specify Odd/Even) Month from July to December Course Name Software Development Fundamentals-I Credits 4 Contact Hours 3 (L) + 1(T) Faculty (Names) Coordinator(s) Archana Purwar ( J62) + Sudhanshu Kulshrestha (J128) Teacher(s) Adwitiya Sinha, Amanpreet Kaur, Chetna Dabas, Dharamveer (Alphabetically) Rajput, Gaganmeet Kaur, Parul Agarwal, Sakshi Agarwal , Sonal, Shradha Porwal COURSE OUTCOMES COGNITIVE LEVELS CO1 Solve puzzles , formulate flowcharts, algorithms and develop HTML Apply Level code for building web pages using lists, tables, hyperlinks, and frames (Level 3) CO2 Show execution of SQL queries using MySQL for database tables and Understanding Level retrieve the data from a single table. (Level 2) CO 3 Develop python code using the constructs such as lists, tuples, Apply Level dictionaries, conditions, loops etc. and manipulate the data stored in (Level 3) MySQL database using python script. CO4 Develop C Code for simple computational problems using the control Apply Level structures, arrays, and structure. (Level 3) CO5 Analyze a simple computational problem into functions and develop a Analyze Level complete program. (Level 4) CO6 Interpret different data representation , understand precision, Understanding Level accuracy and error (Level 2) Module Title of the Module Topics in the Module No. of Lectures for No. the module 1. Introduction to Introduction to HTML, Tagging v/s Programming, 5 Scripting Algorithmic Thinking and Problem Solving, Introductory algorithms and flowcharts Language & Algorithmic Thinking 2. Developing simple Developing simple applications using python; data 4 software types (number, string, list), operators, simple input applications with output, operations, control flow (if -else, while) scripting and visual languages 3. -

03 Algorithmics Linear.6Up.Pdf
08.09.20 Big-Oh notation classes Algorithmics (6EAP) Class Informal Intuition Analogy MTAT.03.238 f(n) ∈ ο ( g(n) ) f is dominated by g Strictly below < Bounded from above Upper bound Linear structures, sorting, f(n) ∈ O( g(n) ) ≤ Bounded from “equal to” searching, Recurrences, f(n) ∈ Θ( g(n) ) above and below = Master Theorem... Bounded from below Lower bound f(n) ∈ Ω( g(n) ) ≥ Jaak Vilo f(n) ∈ ω( g(n) ) f dominates g Strictly above > 2020 Fall Jaak Vilo 1 Linear, sequential, ordered, list … Physical ordered list ~ array • Memory /address/ – Garbage collection • Files (character/byte list/lines in text file,…) • Disk – Disk fragmentation Memory, disk, tape etc – is an ordered sequentially addressed media. Data structures Linear data structures: Arrays • https://en.wikipedia.org/wiki/List_of_data_structures • Array • Hashed array tree • Bidirectional map • Heightmap • Bit array • Lookup table • https://en.wikipedia.org/wiki/List_of_terms_relating_to_algo • Bit field • Matrix rithms_and_data_structures • Bitboard • Parallel array • Bitmap • Sorted array • Circular buffer • Sparse array • Control table • Sparse matrix • Image • Iliffe vector • Dynamic array • Variable-length array • Gap buffer 1 08.09.20 Linear data structures: Lists Lists: Array • Doubly linked list 0 1 size MAX_SIZE-1 • Array list • Xor linked list 3 6 7 5 2 • Linked list • Zipper • Self-organizing list • Doubly connected edge L = int[MAX_SIZE] • Skip list list L[2]=7 • Unrolled linked list • Difference list • VList Lists: Array Multiple lists, 2-D-arrays, etc… 0 1 size -

Binary Trees, While 3-Ary Trees Are Sometimes Called Ternary Trees
Rooted Tree A rooted tree is a tree with a countable number of nodes, in which a particular node is distinguished from the others and called the root: In some contexts, in which only a rooted tree would make sense, the term tree is often used. Infinite Tree A rooted tree is infinite if it contains a countably infinite number of nodes. Finite Tree Similarly, a rooted tree is finite if it contains a finite number of nodes. Parent Consider a rooted tree T whose root is r T Let t be a node of T From Paths in Trees are Unique, there is only one path from t to r T Let π:T−{r T }→T be the mapping defined as: π(t)= the node adjacent to t on the path to r T Then π(t) is known as the parent (or parent node) of t , and π as the parent function or parent mapping. Root Node The root node, or just root, is the one node in a rooted tree which, by definition, has no parent. Ancestor An ancestor (or ancestor node) of a node t of a rooted tree T whose root is r T is a node in the path from t to r T . Thus, the root of a rooted tree T is the ancestor of every node of T (including itself). Proper Ancestor A proper ancestor of a node t is an ancestor of t which is not t itself. Children The children (or child nodes) of a node t in a rooted tree T are the elements of the set: {s∈T:π(s)=t} That is, the children of t are all the nodes of T of which t is the parent. -

Insert a New Element Before Or After the Kth Element – Delete the Kth Element of the List
Algorithmics (6EAP) MTAT.03.238 Linear structures, sorting, searching, Recurrences, Master Theorem... Jaak Vilo 2020 Fall Jaak Vilo 1 Big-Oh notation classes Class Informal Intuition Analogy f(n) ∈ ο ( g(n) ) f is dominated by g Strictly below < f(n) ∈ O( g(n) ) Bounded from above Upper bound ≤ f(n) ∈ Θ( g(n) ) Bounded from “equal to” = above and below f(n) ∈ Ω( g(n) ) Bounded from below Lower bound ≥ f(n) ∈ ω( g(n) ) f dominates g Strictly above > Linear, sequential, ordered, list … Memory, disk, tape etc – is an ordered sequentially addressed media. Physical ordered list ~ array • Memory /address/ – Garbage collection • Files (character/byte list/lines in text file,…) • Disk – Disk fragmentation Data structures • https://en.wikipedia.org/wiki/List_of_data_structures • https://en.wikipedia.org/wiki/List_of_terms_relating_to_algo rithms_and_data_structures Linear data structures: Arrays • Array • Hashed array tree • Bidirectional map • Heightmap • Bit array • Lookup table • Bit field • Matrix • Bitboard • Parallel array • Bitmap • Sorted array • Circular buffer • Sparse array • Control table • Sparse matrix • Image • Iliffe vector • Dynamic array • Variable-length array • Gap buffer Linear data structures: Lists • Doubly linked list • Array list • Xor linked list • Linked list • Zipper • Self-organizing list • Doubly connected edge • Skip list list • Unrolled linked list • Difference list • VList Lists: Array 0 1 size MAX_SIZE-1 3 6 7 5 2 L = int[MAX_SIZE] L[2]=7 Lists: Array 0 1 size MAX_SIZE-1 3 6 7 5 2 L = int[MAX_SIZE] L[2]=7 L[size++] -

Data Structures
Data structures PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Thu, 17 Nov 2011 20:55:22 UTC Contents Articles Introduction 1 Data structure 1 Linked data structure 3 Succinct data structure 5 Implicit data structure 7 Compressed data structure 8 Search data structure 9 Persistent data structure 11 Concurrent data structure 15 Abstract data types 18 Abstract data type 18 List 26 Stack 29 Queue 57 Deque 60 Priority queue 63 Map 67 Bidirectional map 70 Multimap 71 Set 72 Tree 76 Arrays 79 Array data structure 79 Row-major order 84 Dope vector 86 Iliffe vector 87 Dynamic array 88 Hashed array tree 91 Gap buffer 92 Circular buffer 94 Sparse array 109 Bit array 110 Bitboard 115 Parallel array 119 Lookup table 121 Lists 127 Linked list 127 XOR linked list 143 Unrolled linked list 145 VList 147 Skip list 149 Self-organizing list 154 Binary trees 158 Binary tree 158 Binary search tree 166 Self-balancing binary search tree 176 Tree rotation 178 Weight-balanced tree 181 Threaded binary tree 182 AVL tree 188 Red-black tree 192 AA tree 207 Scapegoat tree 212 Splay tree 216 T-tree 230 Rope 233 Top Trees 238 Tango Trees 242 van Emde Boas tree 264 Cartesian tree 268 Treap 273 B-trees 276 B-tree 276 B+ tree 287 Dancing tree 291 2-3 tree 292 2-3-4 tree 293 Queaps 295 Fusion tree 299 Bx-tree 299 Heaps 303 Heap 303 Binary heap 305 Binomial heap 311 Fibonacci heap 316 2-3 heap 321 Pairing heap 321 Beap 324 Leftist tree 325 Skew heap 328 Soft heap 331 d-ary heap 333 Tries 335 Trie -

Course Description
Detailed Syllabus Lecture-wise Breakup Course Code 15B11CI611 Semester Even Semester 6th Session 2018 -2019 (specify Odd/Even) Month from January Course Name Theory of Computation and Compiler Design Credits 4 (3-1-0) Contact Hours 4 Faculty (Names) Coordinator(s) Ambalika Sarkar Teacher(s) Mukta Goel (Alphabetically) Sanjeev Patel COURSE OUTCOMES COGNITIVE LEVELS Understand the regular expression, regular languages, context free Understand level (C2) C314.1 languages and its acceptance using automata. Identify the phases of compilers for a programming language and Apply Level (C3) C314.2 construct the parsing table for a given syntax Build syntax directed translation schemes for a given context free Analyze Level (C4) C314.3 grammar by analyzing S-attributed and L-attributed grammars. Construct grammars and machines for a context free and context Apply Level (C3) C314.4 sensitive languages. Generate the intermediate code and utilize various optimization Apply Level (C3) C314.5 techniques to generate low level code for high level language program. Module Title of the Topics in the Module No. of No. Module Lectures for the module 1. Unit-1 Finite automata: 14 Review of Automata, its types and regular expressions, Equivalence of NFA, DFA and €-NFA, Conversion of automata and regular expression, Applications of Finite Automata to lexical analysis. [14 L] 2. Unit-2 PDA and Parser: Push down automata, Context Free 12 grammars, top down and bottom up parsing, YACC programming specification [12 L] 3. Unit-3 Chomsky hierarchy and Turing Machine: Chomsky 6 hierarchy of languages and recognizers, Context Sensitive features like type checking, Turing Machine as language acceptors and its design.[6L] 4. -

Set and Map Adts: Left-Leaning Red-Black Trees CSE 373 Winter 2020
L09: Left-Leaning Red-Black Trees CSE373, Winter 2020 Set and Map ADTs: Left-Leaning Red-Black Trees CSE 373 Winter 2020 Instructor: Hannah C. Tang Teaching Assistants: Aaron Johnston Ethan Knutson Nathan Lipiarski Amanda Park Farrell Fileas Sam Long Anish Velagapudi Howard Xiao Yifan Bai Brian Chan Jade Watkins Yuma Tou Elena Spasova Lea Quan L09: Left-Leaning Red-Black Trees CSE373, Winter 2020 Announcements ❖ Case-vs-Asymptotic Analysis handout released! ▪ https://courses.cs.washington.edu/courses/cse373/20wi/files/clarity _case_asymp.pdf ❖ Workshop Survey released (see Piazza) ▪ Workshop Friday @ 11:30am, CSE 203 3 L09: Left-Leaning Red-Black Trees CSE373, Winter 2020 Lecture Outline ❖ Review: 2-3 Trees and BSTs ❖ Left-Leaning Red-Black Trees ▪ Insertion ❖ Other Balanced BSTs 4 L09: Left-Leaning Red-Black Trees CSE373, Winter 2020 Review: BSTs and B-Trees ❖ Search Trees have great runtimes most of the time ▪ But they struggle with sorted (or mostly-sorted) input ▪ Must bound the height if we need runtime guarantees ❖ Plain BSTs: simple to reason about/implement. A good starting point ❖ B-Trees are a Search Tree variant that binds the height to Θ(log N) by only allowing the tree to grow from its root ▪ A good choice for a Map and/or Set implementation LinkedList BST Map, B-Tree Map, Map, Worst Worst Case Worst Case Case Find Θ(N) h = Θ(N) Θ(log N) Add Θ(N) h = Θ(N) Θ(log N) Remove Θ(N) h = Θ(N) Θ(log N) 5 L09: Left-Leaning Red-Black Trees CSE373, Winter 2020 Review: 2-3 Trees ❖ 2-3 Trees are a specific type of B-Tree (with L=3) ❖ Its invariants are the same as a B-Tree’s: 1. -

Lecture 04 Linear Structures Sort
Advanced Algorithmics (6EAP) MTAT.03.238 Linear structures, sor.ng, searching, etc Jaak Vilo 2014 Fall Jaak Vilo 1 Big-Oh notaon classes Class Informal Intuion Analogy f(n) ∈ ο ( g(n) ) f is dominated by g Strictly below < f(n) ∈ O( g(n) ) Bounded from above Upper bound ≤ f(n) ∈ Θ( g(n) ) Bounded from “equal to” = above and below f(n) ∈ Ω( g(n) ) Bounded from below Lower bound ≥ f(n) ∈ ω( g(n) ) f dominates g Strictly above > Conclusions • Algorithm complexity deals with the behavior in the long-term – worst case -- typical – average case -- quite hard – best case -- bogus, “chea9ng” • In pracGce, long-term someGmes not necessary – E.g. for sorGng 20 elements, you don’t need fancy algorithms… Linear, sequenGal, ordered, list … Memory, disk, tape etc – is an ordered sequentially addressed media. Physical ordered list ~ array • Memory /address/ – Garbage collecGon • Files (character/byte list/lines in text file,…) • Disk – Disk fragmentaon Linear data structures: Arrays • Array • Hashed array tree • BidirecGonal map • Heightmap • Bit array • Lookup table • Bit field • Matrix • Bitboard • Parallel array • Bitmap • Sorted array • Circular buffer • Sparse array • Control table • Sparse matrix • Image • Iliffe vector • Dynamic array • Variable-length array • Gap buffer Linear data structures: Lists • Doubly linked list • Array list • Xor linked list • Linked list • Zipper • Self-organizing list • Doubly connected edge • Skip list list • Unrolled linked list • Difference list • VList Lists: Array 0 1 size MAX_SIZE-1 3 6 7 5 2 L = int[MAX_SIZE] L[2]=7 -

Cara Kerja B-Tree Dan Aplikasinya
Cara Kerja B-tree dan Aplikasinya Paskasius Wahyu Wibisono - 13510085 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia [email protected] Abstrak – B-tree adalah implementasi khusus dari Pada gambar di atas, dapat kita lihat beberapa elemen struktur data pohon. B-tree memungkinkan data tetap dari sebuah pohon berakar terurut. Proses penambahan data, penghapusan data, dan • b dan c adalah anak dari a pencarian juga dapat dilakukan dengan efisien. B-tree juga • bagus dalam membagi data ke beberapa media penyimpanan d dan e adalah anak dari c berbeda, sehingga efektif untuk digunakan pada data • a adalah simpul akar berukuran besar. Di dalam makalah ini akan dijelaskan cara • b, d, dan e adlah simpul daun kerja B-tree, variasi, dan berbagai aplikasinya. • c adalah simpul dalam Pohon sering kali dipakai dalam kehidupan sehari-hari Kata kunci – pohon, b-tree, basis data, berkas sistem. maupun dalam bidang informatika. Dalam kehidupan sehari-hari, pohon antara lain dipakai untuk I. PENDAHULUAN menggambarkan silsilah keluarga, struktur kepengurusan organisasi, pengambilan keputusan, penjadwalan Dalam teori graf, pohon adalah graf tak berarah di pertandingan olahraga, dan lain-lain. mana dua simpul acak hanya terhubung oleh tepat satu Sementara dalam bidang informatika, pohon digunakan lintasan. Dengan kata lain, pohon adalah graf terhubung sebagai sebuah struktur data. Pohon digunakan karena yang tidak memiliki siklus. Graf tak terhubung yang memiliki beberapa kelebihan dibandingkan struktur data semua elemennya adalah pohon disebut sebagai hutan. lain. Kelebihan-kelebihan itu antara lain dalam algoritma Simpul 'teratas' pada sebuah pohon berakar, yaitu simpul pencarian dan pengurutan, serta menjadi basis untuk yang tidak memiliki simpul orang tua disebut juga sebagai struktur data lain seperti set, multiset, dan larik asosiatif.