NLSRT Memo No
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
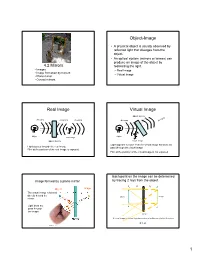
Mirrors Or Lenses) Can Produce an Image of the Object by 4.2 Mirrors Redirecting the Light
Object-Image • A physical object is usually observed by reflected light that diverges from the object. • An optical system (mirrors or lenses) can produce an image of the object by 4.2 Mirrors redirecting the light. • Images – Real Image • Image formation by mirrors – Virtual Image • Plane mirror • Curved mirrors. Real Image Virtual Image Optical System ing diverging erg converging diverging diverging div Object Object real Image Optical System virtual Image Light appears to come from the virtual image but does not Light passes through the real image pass through the virtual image Film at the position of the real image is exposed. Film at the position of the virtual image is not exposed. Each point on the image can be determined Image formed by a plane mirror. by tracing 2 rays from the object. B p q B’ Object Image The virtual image is formed directly behind the object image mirror. Light does not A pass through A’ the image mirror A virtual image is formed by a plane mirror at a distance q behind the mirror. q = -p 1 A mirror reverses front and back Parabolic Mirrors Optic Axis object mirror image mirror The mirror image is different from the object. The z direction is reversed in the mirror image. Parallel rays reflected by a parabolic mirror are focused at a point, called the Focal Point located on the optic axis. Your right hand is the mirror image of your left hand. Parabolic Reflector Spherical mirrors • Spherical mirrors can be used to form images • Spherical mirrors are much easier to fabricate than parabolic mirrors • A spherical mirror is an approximation of a parabolic mirror for small curvatures. -

On the Burning Mirrors of Archimedes, with Some Propositions Relating to the Concentration of Light Produced by Reectors of Different Forms
Transactions of the Royal Society of Edinburgh http://journals.cambridge.org/TRE Additional services for Transactions of the Royal Society of Edinburgh: Email alerts: Click here Subscriptions: Click here Commercial reprints: Click here Terms of use : Click here IV.—On the Burning Mirrors of Archimedes, with some Propositions relating to the concentration of Light produced by Reectors of different forms John Scott Transactions of the Royal Society of Edinburgh / Volume 25 / Issue 01 / January 1868, pp 123 - 149 DOI: 10.1017/S0080456800028143, Published online: 17 January 2013 Link to this article: http://journals.cambridge.org/abstract_S0080456800028143 How to cite this article: John Scott (1868). IV.—On the Burning Mirrors of Archimedes, with some Propositions relating to the concentration of Light produced by Reectors of different forms. Transactions of the Royal Society of Edinburgh, 25, pp 123-149 doi:10.1017/S0080456800028143 Request Permissions : Click here Downloaded from http://journals.cambridge.org/TRE, IP address: 129.93.16.3 on 13 Apr 2015 ( 123 ) IV.—On the Burning Mirrors of Archimedes, with some Propositions relating to the concentration of Light produced by Reflectors of different forms. By JOHN SCOTT, Esq., Tain. (Plate III.) (Bead 6th January 1868). As the reputed fact of ARCHIMEDES having burned the Roman ships engaged in the siege of Syracuse, by concentrating on them the solar rays, has not only been doubted but disbelieved by some of the most eminent scientific men, I shall briefly give the evidence on both sides. The burning of the ships of MARCELLUS is mentioned by most of the ancient writers who refer to the machines which ARCHIMEDES employed in the defence of his native city, and their statements have been repeated by succeeding authors, without any doubts having been expressed until comparatively recent times. -

Caliper Application Summary Report 20: LED PAR38 Lamps
Application Summary Report 20: LED PAR38 Lamps November 2012 Addendum September 2013 Prepared for: Solid-State Lighting Program Building Technologies Office Office of Energy Efficiency and Renewable Energy U.S. Department of Energy Prepared by: Pacific Northwest National Laboratory 1 Preface The U.S. Department of Energy (DOE) CALiPER program has been purchasing and testing general illumination solid-state lighting (SSL) products since 2006. CALiPER relies on standardized photometric testing (following the 1 Illuminating Engineering Society of North America [IES] approved method LM-79-08 ) conducted by accredited, 2 independent laboratories. Results from CALiPER testing are available to the public via detailed reports for each product or through summary reports, which assemble data from several product tests and provide comparative 3 analyses. It is not possible for CALiPER to test every SSL product on the market, especially given the rapidly growing variety of products and changing performance characteristics. Starting in 2012, each CALiPER summary report focuses on a single product type or application. Products are selected with the intent of capturing the current state of the market—a cross section ranging from expected low to high performing products with the bulk characterizing the average of the range. The selection does not represent a statistical sample of all available 4 products. To provide further context, CALiPER test results may be compared to data from LED Lighting Facts, 5 ™ ENERGY STAR® performance criteria, technical requirements for the DesignLights Consortium (DLC) Qualified 6 Products List (QPL), or other established benchmarks. CALiPER also tries to purchase conventional (i.e., non- SSL) products for comparison, but because the primary focus is SSL, the program can only test a limited number. -

The Cassegrain Antenna
The Cassegrain Antenna Principle of a Cassegrain telescope: a convex secondary reflector is located at a concave primary reflector. Figure 1: Principle of a Cassegrain telescope Sieur Guillaume Cassegrain was a French sculptor who invented a form of reflecting telescope. A Cassegrain telescope consists of primary and secondary reflecting mirrors. In a traditional reflecting telescope, light is reflected from the primary mirror up to the eye-piece and out the side the telescope body. In a Cassegrain telescope, there is a hole in the primary mirror. Light enters through the aperture to the primary mirror and is reflected back up to the secondary mirror. The viewer then peers through the hole in the primary reflecting mirror to see the image. A Cassegray antenna used in a fire-control radar. Figure 2: A Cassegray antenna used in a fire-control radar. In telecommunication and radar use, a Cassegrain antenna is an antenna in which the feed radiator is mounted at or near the surface of a concave main reflector and is aimed at a convex subreflector. Both reflectors have a common focal point. Energy from the feed unit (a feed horn mostly) illuminates the secondary reflector, which reflects it back to the main reflector, which then forms the desired forward beam. Advantages Disadvantage: The subreflectors of a Cassegrain type antenna are fixed by bars. These bars The feed radiator is more easily and the secondary reflector constitute supported and the antenna is an obstruction for the rays coming geometrically compact from the primary reflector in the most effective direction. It provides minimum losses as the receiver can be mounted directly near the horn. -

Optical Design of a Solar Parabolic Thermal Concentrator Based On
Optical Design of a Solar Parabolic Thermal Concentrator Based on Trapezoidal Reflective Petals Saša Pavlović*, Darko Vasiljević+, Velimir Stefanović* *Faculty of Mechanical Engineering University of Nis, Thermal Engineering Department *Aleksandra Medvedeva 14, 18000 Niš, Serbia, [email protected], [email protected] +Institute of Physics, Photonics Center Pregravica 118 , 11080 Belgrade, Serbia [email protected] Abstract— In this paper detailed optical of the solar parabolic tracing software for evaluation of the optical performance of a dish concentrator is presented. The system has diameter D = static 3-D Elliptical Hyperboloid Concentrator (EHC). 2800 mm and focal length f = 1400mm. The parabolic dish of the Optimization of the concentrator profile and geometry is solar system consists from 12 curvilinear trapezoidal reflective carried out to improve the overall performance of system. petals. The total flux on receiver and the distribution of Kashika and Reddy [8] used satellite dish of 2.405 m in irradiance for absorbed flux on center and periphery receiver are given. The goal of this paper is to present optical design of a diameter with aluminium frame as a reflector to reduce the low-tech solar concentrator that can be used as a potentially low- weight of the structure and cost of the solar system. In their cost tool for laboratory-scale research on the medium- solar system the average temperature of water vapor was temperature thermal processes, cooling, industrial processes, 3000C, when the absorber was placed at the focal point. Cost polygeneration systems etc. of their system was US$ 950. El Ouederni et al. [9] was testing parabolic concentrator of 2.2 m in diameter with Keywords— Solar parabolic dish concentrator, Optical analysis, reflecting coefficient 0.85. -

Effect of Reflector Geometry in the Annual Received Radiation
energies Article Effect of Reflector Geometry in the Annual Received Radiation of Low Concentration Photovoltaic Systems João Paulo N. Torres 1,* ID , Carlos A. F. Fernandes 1, João Gomes 2, Bonfiglio Luc 3, Giovinazzo Carine 3, Olle Olsson 2 and P. J. Costa Branco 4 ID 1 Instituto de Telecomunicações, Instituto Superior Técnico, Universidade de Lisboa, 1649-004 Lisboa, Portugal; [email protected] 2 Department of Building, Energy and Environmental Engineering, University of Gävle, 801 76 Gävle, Sweden; [email protected] (J.G.); [email protected] (O.O.) 3 Ecole Polytechnique Universitaire de Montpellier, 34095 Montpellier, France; lucbonfi[email protected] (B.L.); [email protected] (G.C.) 4 Associated Laboratory for Energy, Transports and Aeronautics, Institute of Mechanical Engineering (LAETA, IDMEC), Instituto Superior Técnico, Universidade de Lisboa, 1649-004 Lisboa, Portugal; [email protected] * Correspondence: [email protected]; Tel.: +351-910086958 Received: 6 June 2018; Accepted: 14 July 2018; Published: 19 July 2018 Abstract: Solar concentrator photovoltaic collectors are able to deliver energy at higher temperatures for the same irradiances, since they are related to smaller areas for which heat losses occur. However, to ensure the system reliability, adequate collector geometry and appropriate choice of the materials used in these systems will be crucial. The present work focuses on the re-design of the Concentrating Photovoltaic system (C-PV) collector reflector presently manufactured by the company Solarus, together with an analysis based on the annual assessment of the solar irradiance in the collector. An open-source ray tracing code (Soltrace) is used to accomplish the modelling of optical systems in concentrating solar power applications. -

Optical Design of an LED Motorcycle Headlamp with Compound Reflectors and a Toric Lens
E102 Vol. 54, No. 28 / October 1 2015 / Applied Optics Research Article Optical design of an LED motorcycle headlamp with compound reflectors and a toric lens 1 2, 1 1 WEN-SHING SUN, CHUEN-LIN TIEN, *WEI-CHEN LO, AND PU-YI CHU 1Department of Optics and Photonics, National Central University, Chung-Li 32001, Taiwan 2Department of Electrical Engineering, Feng Chia University, Taichung 40724, Taiwan *Corresponding author: [email protected] Received 31 March 2015; revised 16 July 2015; accepted 16 July 2015; posted 28 July 2015 (Doc. ID 236954); published 21 August 2015 An optical design for a new white LED motorcycle headlamp is presented. The motorcycle headlamp designed in this study comprises a white LED module, an elliptical reflector, a parabolic reflector, and a toric lens. The light emitted from the white LED module is located at the first focal point of the elliptical reflector and focuses on the second focal point. The second focal point of the elliptical reflector and the focal point of the parabolic reflector are confocal. We use nonsequential rays to improve the optical efficiency of the compound reflectors. The toric spherical lens allows the device to meet the Economic Commission of Europe, regulation no. 113 (ECE R113). Furthermore, good uniformity is obtained by using aspherical surface optimization of the same toric lens. The reflectivity of the reflector is 95%, and the transmittance of each lens surface is 98%. The average deviation of the high beam is 14.17%, and the optical efficiency is 66.45%. © 2015 Optical Society of America OCIS codes: (080.4228) Nonspherical mirror surfaces; (080.4295) Nonimaging optical systems; (220.2945) Illumination design; (220.4298) Nonimaging optics. -

Powerful LED-Based Train Headlight Optimized for Energy Savings 13 February 2018
Powerful LED-based train headlight optimized for energy savings 13 February 2018 incandescent or halogen bulbs, are bright enough to meet safety regulations but are not very energy efficient because most of the energy powering the light is converted into heat rather than visible light. Researchers led by Guo-Dung J. Su from the Micro Optics Device Laboratory of the Graduate Institute of Photonics and Optoelectronics at National Taiwan University, Taiwan, were approached by the engineering and design company Lab H2 Inc., to design locomotive headlights that use LEDs as a light source. In addition to requiring less energy, LEDs also last longer and are smaller and more rugged than traditional light sources. "Some LED headlight products sold on the market are designed with many LEDs that have outputs that overlap in large sections. These designs waste a lot of energy," said Wei-Lun Liang of the Micro Optics Device Laboratory, who was instrumental in A new train headlight design uses two half-circular designing the new train headlight. "Our research parabolic, or cup-shaped, aluminized reflectors with high- showed that electricity use can be reduced by efficiency LEDs placed in the plane where the two focusing on the best way to distribute the LED reflectors come together. Combining the strong beams from each reflector generates the light intensity energy equally." necessary to meet safety guidelines. Credit: Wei-Lun Liang, National Taiwan University In The Optical Society journal Applied Optics, Liang and Su report a new train headlight design based on ten precisely positioned high efficiency LEDs. The design uses a total of 20.18 Watts to Researchers have designed a new LED-based accomplish the same light intensity as an train headlight that uses a tenth of the energy incandescent or halogen lamp that uses several required for headlights using conventional light hundred watts. -

Cylindrical SKA Concept
Authors: John D. Bunton CSIRO Telecommunications and Industrial Physics Carole A. Jackson RSAA, Australian National University Elaine M. Sadler School of Physics, University of Sydney Submitted to the SKA Engineering and Management Team by The Executive Secretary Australian SKA Consortium Committee PO Box 76, Epping, NSW 1710, Australia June 2002 Updated 11 July 2002 17 Jul 02 Release 1 CSIRO Table of contents Table of contents ................................................................................................................. 2 Executive summary............................................................................................................. 5 1 Introduction..................................................................................................................6 1.1 Relative Costs: the best of both worlds................................................................. 7 1.2 Instrument Overview............................................................................................. 7 2 Science Drivers .......................................................................................................... 10 2.1 Milky Way and local galaxies............................................................................. 10 2.2 Transient phenomena .......................................................................................... 10 2.3 Early Universe and large-scale structure ............................................................ 11 2.4 Galaxy formation ............................................................................................... -

Electrodynamics Optimization Reflected Intensity of Linearly
International Journal of Innovations in Engineering and Technology (IJIET) http://dx.doi.org/10.21172/ijiet.144.12 Electrodynamics Optimization Reflected Intensity of Linearly Polarized Electromagnetic Plane Wave from a Parabolic Cylinder Boundary Interface between Two Different Optical Mediums Hossein Arbab1, Mehdi Rezagholizadeh2 1Department of physics, Faculty of Science, University of Kashan, Kashan, Isfahan state, I. R. of Iran 2Center of intelligent Machines, Department of electrical and computer engineering, McGill University, Quebec, Canada Abstract- The aim of this study is investigate the dependence of reflected intensity of linearly polarized electromagnetic plane wave from a parabolic cylinder boundary interface. The opening area of device is kept constant but its focal length would be changed. For this purpose, a discrete mathematical modeling is applied. We apply this model to a non - integrated parabolic mirror as well as a smooth and continuous one. In this model a cylindrical parabolic reflector is divided into definite number of thin long strips (number of strips depends on the focal length of device and width of the strips). Such a model is chosen, because it would be matched with an innovative fabrication method of a special type of parabolic mirror which is fabricated on the basis of this method. This method of fabrication has been published in details for circular parabolic mirrors in the journal of optics (optical society of India). At the present paper we investigate optimum reflected power by a parabolic trough interface between two different optical mediums. Results of calculations show that if the opening area of interface is kept constant but its focal length is changing, then reflected power would be depended on the focal length of the parabolic mirror, optical properties of the reflecting surface, state of polarization of incoming wave, configuration of interface with plane of incidence and wavelength of the incoming wave. -

Concentrating Collectors
Sustainable Energy Science and Engineering Center Concentrating Collectors Collectors are oriented to track the sun so that the beam radiation will be directed onto the absorbing surface Collector: Receiver and the concentrator Receiver: Radiation is absorbed and converted to some other energy form (e.g. heat). Concentrator: Collector that directs radiation onto the receiver. The aperture of the concentrator is the opening through which the solar radiation enters the concentrator Source: Chapter 7 of Solar Engineering of thermal processes by Duffie & Beckman, Wiley, 1991 Reference: http://www.powerfromthesun.net/book.htm Sustainable Energy Science and Engineering Center Collector Configurations Goal: Increasing the radiation flux on receivers a) Tubular absorbers with diffusive back reflector; b) Tubular absorbers with specular cusp reflector; c) Plane receiver with plane reflector; d) parabolic concentrator; e) Fresnel reflector f) Array of heliostats with central receiver Sustainable Energy Science and Engineering Center Concentrating Collectors Fresnel Lens: An optical device for concentrating light that is made of concentric rings that are faced at different angles so that light falling on any ring is focused to the same point. Parabolic trough collector: A high-temperature (above 360K) solar thermal concentrator with the capacity for tracking the sun using one axis of rotation. It uses a trough covered with a highly reflective surface to focus sunlight onto a linear absorber containing a working fluid that can be used for medium temperature space or process heat or to operate a steam turbine for power or electricity generation. Central Receiver: Also known as a power tower, a solar power facility that uses a field of two-axis tracking mirrors known as heliostat (A device that tracks the movement of the sun). -

Conventional Parabolic Single Dishes the Green Bank Telescope
Conventional Parabolic Single Dishes and the Green Bank Telescope Single Dish Summer School August 2003 Phil Jewell National Radio Astronomy Observatory Green Bank Parabolic Single Dishes • The most common type of single dish radio telescope (beginning with the Reber Telescope in 1937) is a Parabolic Reflector with ‣ Azimuth/Elevation mount • Azimuth motion by wheel & track or azimuth bearing • Some older telescopes are Equatorially mounted – e.g., the 140 Foot Telescope ‣ Symmetric feed supports for one or both of • Prime focus feeds • Subreflector (secondary reflector) – With Cassegrain or Gregorian Optics • The GBT is a special case of this: • an unblocked section of a parabola. Parabolic Single Dishes • Comparatively straightforward to build and structurally analyze • Have circular, easy-to-interpret beam shapes • Appropriate for wavelengths from ~1 m to the sub-millimeter • Other designs may be more appropriate for longer wavelengths and for achieving very large collecting areas Major Parabolic Single Dishes of the World • The large majority of the 54 single dish telescopes listed in the school volume article by Chris Salter (p493ff) are conventional paraboloids of this type. We will highlight only a few here: ‣ Centimeter-wave telescopes: • MPIfR Effelsberg 100m • Parkes 64 m • Lovell Telescope ‣ Millimeter/submm-wave telescopes • Kitt Peak 12 m • IRAM 30 m Telescope • James Clerk Maxwell Telescope (JCMT) • Caltech Submillimeter Observatory (CSO) • Heinrich Hertz Telescope (SMTO/HHT) • Large Millimeter Telescope (LMT/GTM) ‣ Centimeter/Millimeter-wave