DOCSLIB.ORG

고분자의 변형과 파괴 (Deformation and Fracture of Polymers)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
고분자의 변형과 파괴 (Deformation and Fracture of Polymers) ChapterChapter 1111 MechanicalMechanical BehaviorBehavior ofof PolymersPolymers ContentsContents 1. Outline 2. Stress and Strain 3. Small-Strain Deformation 4. Yield 5. Crazing 6. Fracture OutlineOutline (1)(1) ▶ mechanical property ▷ mechanical response of a material to the applied stress (load) ▶ response of a polymer depends on ▷ material (chemical structure) ▷ morphology (physical structure) ▷ temperature ▷ time ▷ magnitude of stress ▷ state of stress OutlineOutline (2)(2) ▶ magnitude of stress σ ▷ upon small stresses brittle • elastic deformation yield • viscous deformation (flow) ductile • viscoelastic deformation ▷ upon large stresses elastomeric • plastic deformation • yielding Æ ductile 0.1 1 ε • crazing Æ brittle • failure (fracture) Fig 11.4 p562 tough Æ ductile ▶ response of the polymer chains ▷ deformations of the bond lengths and angles ▷ uncoiling of the chains ▷ slippage of the chains ▷ scission of the chains Fig 11.3 p562 StressStress andand strainstrain ▶ stress: load (force) per unit area, σ = F/A [N/m2 = Pa] ▶ strain: displacement by load, ε = ΔL/L [dimensionless] ▶ engineering (nominal) stress, s = F/A0 ▶ true (natural) stress, σ = F/A ▶ engineering (nominal) strain, e = ΔL/L0 ▶ true (natural) strain, dε = dL/L, ε = ln (L/L0) ▷ ε = ln (L/L0) = ln [(L0+ΔL)/L0] = ln [1+e] ▷ ε ~ e for small strains only (e < 0.01) ▶ For UTT, s < σ and ε < e TestingTesting geometrygeometry andand statestate ofof stressstress (1)(1) ▶ uniaxial tension σxx = σ > 0 , all other stresses = 0 ▶ uniaxial compression σxx = σ < 0, all other stresses = 0 ▶ simple shear ~ torsion τxy = τ, all other stresses = 0 y x z TestingTesting geometrygeometry andand statestate ofof stressstress (2)(2) ▶ plane stress y σzz = τzx = τyz =0 x z ▶ plane strain y εyy = 0, σyy = ν (σxx + σzz) x z ▶ bending or flexure ConstitutiveConstitutive equationequation (1)(1) ▶ Equations that relate stress to strain (rate) σ = c ε c : stiffness ε = s σ s : compliance ▶ c, s tensors ~ 81 components (9 x 9) ▶ by symmetry in σ, ε (equilibrium), 81 Æ 36 (6 x 6) ▶ by symmetry in c, s 36 Æ 21 ▶ by symmetry in material, 21 → 13 (1 sym pl) → 9 (3 sym pl) → 5 (fiber sym) → 2 (isotropic) linear elastic ▶ For isotropic linear elastic solid in UTT σ non-linear elastic σ(xx) = E ε(xx) (Hooke’s law) εyy = - νεxx ε ConstitutiveConstitutive equationequation (2)(2) ▶ Stiffness and compliance can be time-dependent (viscoelastic), when stress and/or strain are time dependent. ~ viscoelastic behavior ▷ σ(t) = E(t) εo ~ stress relaxation ▷ ε(t) = D(t) σo ~ creep ▶ Stiffness and compliance can be strain-level-dependent (nonlinear), when the stress and/or time exceed linear region. ~ nonlinear behavior ▷ σ(t) = E(t, εo) εo ▶ Stiffness and compliance can be orientation-dependent, when the material is anisotropic (fibers, films). ~ anisotropic behavior Exx ≠ Eyy; νzx ≠ νxy ¾ It is hard to express the real mechanical response in a constitutive equation. ViscoelasticityViscoelasticity ▶ Every material is viscoelastic. ▶ depending on time (strain rate) and temperature ▷ elastic, solid-like ▷ viscoelastic, polymer-like ▷ viscous, liquid-like ▷ Deborah Number = material time / experimental time ▶ VE observation ▷ stress relaxation ▷ creep ▷ recovery ▷ time-temperature superposition ▷ dynamic mechanical ApplicationApplication ofof VEVE DataData toto ProductProduct DesignDesign ▶ Correspondence principle viscoelastic equation Æ elastic equation σ(t) = E(t) ε Æ σ = E ε ▶ Pseudoelasticity From creep, stress relaxation, or isochrone stress-strain curve, estimate long- term stress-strain relation, and design the product. CreepCreep curvescurves andand plotsplots σ↑ different from transient σ−ε curve AnAn exampleexample ofof productproduct designdesign ▶ To design a pressure vessel that is required to be used for 1 year without yielding or fracture (say 5% maximum allowable strain), t r σ = P r / t P σ = 40 MPa t = 109 s ε(t) σ 30 MPa 108 s 107 s 20 MPa 0.05 10 MPa ε 1 yr log t 0.05 LargeLarge deformationdeformation behaviorbehavior ▶ Upon large stress beyond (visco)elastic limit, a polymer experience either yielding or crazing, the two competing processes. ▷ Yielding precedes ductile failure; crazing precedes brittle failure. σ ▷ yield strength (항복강도) ductile ~ stress at yield TS σu brittle (취성) ▷ tensile strength (인장강도) yield strain hardening ~ stress at failure YS σy ▷ elongation at break strain softening (파단신장률) elastomeric ¾ stiff ~ high E ¾ strong ~ high TS ε ε y u ε ¾ ductile ~ high EB after EB yield ▷ ductility (연성) ~ ability to yield and be cold-drawn ¾ tough ~ high energy ▷ toughness (강인성) ~ resistance to crack propagation before fracture YieldYield criteriacriteria ▶ yield = start of plastic deformation ▶ yield by shear only ▶ pressure-dependent YC τmax = σ1 – σ3 = 2C = 2τy = σy ~ polymers σ (comp) = (1.1 – 1.3) σ (tension) ▶ pressure-independent YC y y σ = σ 0 - μ (σ + σ + σ )/3 ~ metals y y 1 2 3 Eqn (11.18) p572 Fig 11.10 p572 σ When all τ’s = 0, then x, y, z are principal axes and y σx, σy, σz are principal stresses (σ1, σ2, σ3). σx σ1 > σ2 > σ3 σz If σx = σy = σz and τ’s = 0, σ1 = σ2 = σ3 (purely hydrostatic) σ1 – σ3 = 0 Æ no yield If σx > 0, and other σ’s & τ’s = 0, σ1 – σ3 = σy Æ yield at σ1 = σy If σ1 = –σ3 and σ2 = 0, σ1 – σ3 = 2σ1 = σy Æ yield at σ1 = τy = σy/2 YieldYield behaviorbehavior ▶ strain rate ÇÆYS Ç ▶ Temp ÇÆYS È !! Fig 11.5 p566 Fig 11.6 & 7 PostPost--yieldyield behaviorbehavior (1)(1) ▶ strian softening ▶ strain hardening ▷ load drop ▷ rise in stress ▷ state of Tg at yield point ▷ orientation of chains Polyethylene σ high mol wt low mol wt ε Epoxy σ low Mc high Mc ε PostPost--yieldyield behaviorbehavior (2)(2) ▶ inhomogeneous deformation ▷ localized instability due to softening, which interacts with restraints ▷ with no restraint ~ necking ▷ with restraint in 1 direction ~ inclined necking ▷ with restrainst in 2 directions ~ shear band PS PMMA Fig 11.9(b) p571 DeformationDeformation ofof semicrystallinesemicrystalline polymerspolymers ▶ semicrystalline = amorphous + crystal (lamellae) ▷ T < Tg < Tm (e.g. PET at RT) • Glass and crystals have comparable mechanical properties. • Yield behavior is similar to amorphous polymers. ▷ Tg < T < Tm (e.g. PE at RT) • crystals in liquid (rubber) • initial deformation (modulus) at rubber. • Only crystals yield: As crystallinity increases, σy increases. ▶ post-yield ~ reorientation of crystals Fig 11.8 p570 CrazingCrazing ▶ localized inhomogeneous plastic deformation by dilatational stress ▷ normal yielding ↔ (shear) yielding ▷ compete with shear yield ▶ structure of craze ▷ long, thin wedge of deformed polymer (microfibrils) Fig 11.9(a) p571 FormationFormation andand growthgrowth ofof crazecraze ▶ Craze initiation criteria No crazing by compression Both craze and yield criteria Fig 11.10 p572 are dependent on Temp and dε/dt. Æ ductile-brittle transition ▶ Craze propagation ▷ thicken by drawing new materials from bulk ▷ lengthen by meniscus instability Fig 11.30 p598 CrazeCraze failurefailure ▶ At very slow strain rates, ▷ fibril breakdown at interface between craze and bulk Æ void ▷ void grows Æ impinge to other voids Æ crack ▷ connecting cracks from other crazes Æ fracture ▶ At high strain rates, ▷ craze fracture ▷ craze fibrils found in fracture surface EnvironmentalEnvironmental stressstress crackingcracking (ESC)(ESC) ▶ Absorbed liquid plasticizes polymer. Æ soften Æ craze at a lower stress Æ fracture ▶ effective when solubility parameter difference is small FractureFracture 9 failure (파쇄, 파단) ~ rupture by exceedingly large stress 9 fracture (파괴) ~ failure by crack propagation ▶ micromechanism of fracture ▷ Chain scission or slip? Fig 11.3 p562, Fig 11.29 p 595 ▷ Upon stress, i) chain slip (against crystal, crosslinking, entanglement) iiA) crazing/yielding or iiB) chain scission (with high Xc, low Mc, low Me) iii) chain scission as stress increases iv) voiding Æ crack Æ fracture DuctileDuctile fracturefracture (1)(1) ▶ failure of shear band ▶ thermal fracture ▷ necking, not stabilized ▷ cone-and-cup failure ▶ diamond cavity ▷ craze blunted by shear band DuctileDuctile fracturefracture (2)(2) ▶ tensile rupture of elastomers ▷ elastomerixc up to failure ▷ ‘failure envelope’ Fig 11.17 p581 • TS vs EB – at different Temp and dε/dt • time – Temp superposition – time to break, tb = εb/(dε/dt) Temp L dε/dt K BrittleBrittle fracturefracture (1)(1) ▶ theoretical strength of solids ▷ σtheo = E/10 Å for interatomic separation ▷ For whiskers, σf ~ E/10 ▷ For isotropic glassy polymers, σf ~ E/100 < σtheo (E ~ 3 GPa, σf < 100 MPa) • due to flaw (crack, notch, inclusion). • stress concentration σmax • plastic constraint F ▶ stress concentration σavg ▷ ahead of crack tip 2b ▷ stress concentration factor, 2a k = σ /σ = 1 + (2a/b) = 1 + 2(a/ρ)1/2 max avg B W BrittleBrittle fracturefracture (2)(2) ▶ plastic constraint ▷ ahead of crack tip ▷ triaxial stress state σ1 > 0 (applied), σ2 & σ3 > 0 (due to crack) ▷ triaxiality Æ yield at higher stress ~ plastic deformation constrained ▷ yield at a stress higher than σc Æ brittle a FractureFracture mechanicsmechanics (1)(1) ▶ Energy balance approach ▷ specimen with crack length 2a ▷ Crack grows when released strain energy by stress (σ2πa/E) is greater than created surface energy (2γ) 1/2 ▷ σf = [2Eγ/πa] : Griffith fracture criterion eqn (11.20) p586 2 2 ▷ for polymers; 2γ ~ 1 J/m , fracture energy (Gc) ~ 100 - 1,000 J/m • Fracture energy higher by other process: plastic deformation at crack tip ▷ replacing 2γ with Gc 1/2 σf = [EGc/πa] for plane stress 2 1/2 σf = [(EGc/π (1-ν )a] for plane strain
Load more

Recommended publications
  • Toughening Behaviour of Rubber-Modified Thermoplastic Polymers Involving Very Small Rubber Particles: 1
    Toughening behaviour of rubber-modified thermoplastic polymers involving very small rubber particles: 1. A criterion for internal rubber cavitation D. Dompas and G. Groeninckx* Catholic University of Leuven, Laboratory of Macrornolecular Structural Chemistry, Celestijnenlaan 20OF, B-3001 Heverlee, Belgium (Received 26 January 1994) The criteria for internal cavitation of rubber particles have been evaluated. It is shown that internal rubber cavitation can be considered as an energy balance between the strain energy relieved by cavitation and the surface energy associated with the generation of a new surface. The model predicts that there exists a critical particle size for cavitation. Very small particles (100-200nm) are not able to cavitate. This critical-particle-size concept explains the decrease in toughening efficiency in different rubber-modified systems involving very small particles. (Keywords: rubber toughening; particle size; rubber cavitation) INTRODUCTION and associated matrix shear yielding is found in rubber-modified PC ~-7, PVC a-x°, poly(butylene tere- Many glassy polymers are brittle. For structural applica- phthalate (PBT) 11, nylon.612-1 s, nylon_6,616 and epoxy tions, this is clearly unwanted and it is well known that systems17 20. The matrix polymers in these rubber- the impact properties can be improved by the incorpora- modified systems are either crosslinked or have a high tion of a dispersed elastomeric phase Lz. The mechanism entanglement density, thus being polymers for which the by which the toughness is enhanced depends on the crazing mechanism is suppressed 21. This is not to say intrinsic ductility of the matrix material and on the that rubber cavitation can only appear in high-entangle- morphology of the blends 3.
    [Show full text]
  • Fatigue Craze Initiation in Polycarbonate: Study by Transmission Electron Microscopy
    Fatigue craze initiation in polycarbonate: study by transmission electron microscopy Hristo A. Hristov, Albert F. Yee* and David W. Gidleyt Department of Materials Science and Engineering and tDepartment of Physics, University of Michigan, Ann Arbor, MI 48109, USA (Received 22 October 1993; revised 26 January 1994) Fatigue craze initiation in bulk, amorphous polycarbonate (PC) is investigated by means of transmission electron microscopy. The results agree very well with small angle X-ray scattering measurements of the same set of samples, and confirm that void generation is the main characteristic of the initiation process. The evolution of the initial void-like structures or 'protocrazes' with dimensions of ~ 50 nm into crazes with dimensions of several micrometres is presented in considerable detail. It is found that some similarities exist between crazes induced by cyclic fatigue at room temperature and crazes produced in monotonic loading at temperatures close to the glass transition. The similarities suggest that disentanglement of polymer chains plays an important role in the fatigue craze initiation process in bulk, amorphous PC near room temperature. (Keywords: fatigue; craze initiation; polycarbonate) INTRODUCTION describing fatigue craze initiation have not been The importance of crazing in the structural integrity of developed either (reviews of the existing models of craze polymeric materials under load was recognized more initiation under constant load can be found in references than 20 years ago, which prompted the beginning of 9 and 16). It seems that optical microscopy (conventional systematic investigations of structure of crazes in and interference optical microscopy) is the most polymers by, among other techniques, transmission frequently used method for studying the gross structure electron microscopy (TEM) 1-4.
    [Show full text]
  • The Growth of Cracks and Crazes in Polymers
    THE GROWTH OF CRACKS AND CRAZES IN POLYMERS - A FRACTURE MECHANICS APPROACH GEORGE PHILIP MARSHALL MARCH W72 A thesis submitted for the degree of Doctor of Philosophy of the University of London and for the Diploma of Imperial College. Department of Mechanical Engineering Imperial College, . London S.W.7. ABSTRACT A study has been made of the use of fracture mechanics in describing crack and craze growth phenomena in plastics. The thesis which follows has been divided into three main parts. Part I has two component chapters. The first (Ch. 2)/ outlines the basis of the fracture mechanics concepts used in the analysis of results and the second chapter (Ch. 3) contains a literature survey of the state of knowledge on crazing and environmental stress cracking in plastics. Part II describes experimental work which has been undertaken to study crack growth phenomena in both air and liquid environments. Chapter 4 gives results obtained from slow crack propagation tests in PMMA in air and shows that there is a unique relationship between the fracture toughness measure Kc and the crack speed. Analysing results on a /crack speed basis is shown to ration- alise results from many different types of test and also accounts for the rate dependent material characteristics. This approach is extended in Chapter 5 to include the effects of crack propagation in polystyrene in air. For the first time, realistic values of fracture toughness have been obtained for the propaga- tion of a single crack/craze system. The Kc vs crack speed relationship is again found to provide a good basis against which results may be compared and dis- cussed.
    [Show full text]
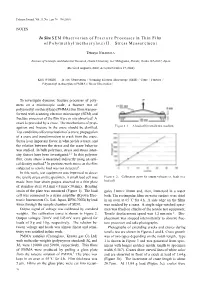
  • In Situ SEM Observation of Fracture Processes in Thin Film of Poly(Methyl Methacrylate) II
    Polymer Journal, Vol.35, No. 1, pp 76—78 (2003) NOTES In Situ SEM Observation of Fracture Processes in Thin Film of Poly(methyl methacrylate) II. Stress Measurement Tetsuya NISHIURA Institute of Scientific and Industrial Research, Osaka University, 8–1 Mihogaoka, Ibaraki, Osaka 567–0047, Japan (Received August 6, 2002; Accepted October 17, 2002) KEY WORDS In situ Observation / Scanning Electron Microscope (SEM) / Craze / Fracture / Poly(methyl methacrylate) (PMMA) / Stress Observation / To investigate dynamic fracture processes of poly- mers on a microscopic scale, a fracture test of poly(methyl methacrylate) (PMMA) thin films was per- formed with scanning electron microscope (SEM) and fracture processes of the film were in situ observed.1 A crack is preceded by a craze. The mechanisms of prop- agation and fracture in the craze should be clarified. Figure 1. A load cell in tensile test machine. Test conditions affect nucleation of a craze, propagation of a craze and transformation to crack from the craze. Stress is an important factor in what yields a craze, and the relation between the stress and the craze behavior was studied. In bulk polymers, stress and stress inten- sity factors have been investigated.2, 3 In thin polymer film, craze stress is measured indirectly using an opti- cal density method.4 In previous work stress on the film subjected to tensile load was not detected.1 In this work, test equipment was improved to detect the tensile stress on the specimen. A small load cell was Figure 2. Calibration curve for output voltages vs. loads in a made from four strain gauges attached to a thin plate load cell.
    [Show full text]
  • Fracture Toughness of Polypropylene-Based Particulate Composites
    Materials 2009, 2, 2046-2094; doi:10.3390/ma2042046 OPEN ACCESS materials ISSN 1996-1944 www.mdpi.com/journal/materials Review Fracture Toughness of Polypropylene-Based Particulate Composites David Arencón and José Ignacio Velasco * Centre Català del Plàstic, Universitat Politècnica de Catalunya, Edifici Vapor Universitari, Colom 114, 08222, Terrassa, Spain; E-Mail: [email protected] (D.A.) * Author to whom correspondence should be addressed; E-Mail: [email protected] (J.I.V.); Tel.: +34 937 837 022; Fax: +34 937 841 827. Received: 27 October 2009; in revised form: 24 November 2009 / Accepted: 27 November 2009 / Published: 30 November 2009 Abstract: The fracture behaviour of polymers is strongly affected by the addition of rigid particles. Several features of the particles have a decisive influence on the values of the fracture toughness: shape and size, chemical nature, surface nature, concentration by volume, and orientation. Among those of thermoplastic matrix, polypropylene (PP) composites are the most industrially employed for many different application fields. Here, a review on the fracture behaviour of PP-based particulate composites is carried out, considering the basic topics and experimental techniques of Fracture Mechanics, the mechanisms of deformation and fracture, and values of fracture toughness for different PP composites prepared with different particle scale size, either micrometric or nanometric. Keywords: polypropylene; composites; fracture toughness 1. Introduction Particulate filled polymers are used in very large quantities in all kinds of applications and despite the overwhelming interest in advanced composite materials, considerable research and development is done on particulate filled polymers even today. Fillers increase stiffness and heat deflection temperatures, decrease shrinkage and improve the appearance of composites [1–3].
    [Show full text]
  • Craze Initiation in Glassy Polymer Systems
    Craze initiation in glassy polymer systems MT02.002 O.F.J.T Bressers Master report Supervisors: dr. ir. J.M.J. den Toonder Philips Research ir. H.G.H. van Melick TU/e dr. ir. L.E. Govaert TU/e prof. dr. ir. H.E.H. Meijer TU/e Summary This report deals with the numerical simulation of craze initiation in amorphous polymer systems. The approach is based on the view that the development of a craze is preceded by de formation of a localised plastic deformation zone. As this zone develops, the hydrostatic stress increases, and, when exceeding a critical stress level, cavitation will take place leading to local development of voids. The voids grow, coalesce and the ligaments between the voids are subsequently super-drawn leading to the typical structure of a craze: a crack-like defect bridged by highly drawn filaments. In Part 1 a critical hydrostatic stress is examined as a cavitation criterion for polymers in a well-defined experiment. A micro indenter with a 150 m sapphire sphere produces reproducible indents, which are later examined with an optical microscope. These observations lead to a critical force where crazes are initiated in polystyrene (PS). Combination of these experiments with a numerical study using the compressible Leonov-model showed that the loading part of the indentation can be accurately predicted. A critical hydrostatic stress of 39MPa is extracted from the numerical model by analysis of the local stress field at the moment the indentation force reaches the experimentally determined force level at which crazes were found to initiate.
    [Show full text]
  • Draft Advisory Circular
    Subject: WINDOWS AND WINDSHIELDS Date: 1/17/03 AC No: 25.775-1 Initiated By: ANM-110 Change: 1. PURPOSE. This advisory circular (AC) sets forth an acceptable means, but not the only means, of demonstrating compliance with the provisions of Title 14, Code of Federal Regulations (14 CFR) part 25 pertaining to the certification requirements for windshields, windows, and mounting structure. Guidance information is provided for showing compliance with § 25.775(d), relating to structural design of windshields and windows for airplanes with pressurized cabins. Terms used in this AC, such as “shall” or “must,” are used only in the sense of ensuring applicability of this particular method of compliance when the acceptable method of compliance described herein is used. Other methods of compliance with the requirements may be acceptable. While these guidelines are not mandatory, they are derived from extensive Federal Aviation Administration (FAA) and industry experience in determining compliance with 14 CFR. This AC does not change, create any additional, authorize changes in, or permit deviations from, regulatory requirements. 2. APPLICABILITY. This advisory circular contains guidance for the latest amendment of the regulations and applies to all transport category airplanes approved under the provisions of part 25, for which a new, amended, or supplemental type certificate is requested. 3. RELATED DOCUMENTS. a. Title 14, Code of Federal Regulations (14 CFR) part 25. § 25.775 Windshields and windows. § 25.365 Pressurized compartment loads. AC 25.775-1 1/17/03 § 25.773(b)(2)(ii) Pilot compartment view. § 25.571 Damage-tolerance and fatigue evaluation of structure. 4.
    [Show full text]
  • Fracture of Dental Materials
    Chapter 4 Fracture of Dental Materials Karl-Johan Söderholm Additional information is available at the end of the chapter http://dx.doi.org/10.5772/48354 1. Introduction Finding a material capable of fulfilling all the requirements needed for replacing lost tooth structure is a true challenge for man. Many such restorative materials have been explored through the years, but the ideal substitute has not yet been identified. What we use today for different restorations are different metals, polymers and ceramics as well as combina- tions of these materials. Many of these materials work well even though they are not perfect. For example, by coating and glazing a metal crown shell with a ceramic, it is possible to make a strong and aesthetic appealing crown restoration. This type of crown restoration is called a porcelain-fused-to-metal restoration, and if such crowns are properly designed, they can also be soldered together into so called dental bridges. The potential problem with these crowns is that the ceramic coating may chip with time, which could require a complete re- make of the entire restoration. Another popular restorative material consists of a mixture of ceramic particles and curable monomers forming a so called dental composite resin. These composites resins can be bonded to cavity walls and produce aesthetic appealing restorations. A potential problem with these restorations is that they shrink during curing and sometimes debond and fracture. In addition to porcelain-fused-to-metal crowns and composites, all- ceramic and metallic restorations as well as polymer based dentures are also commonly used.
    [Show full text]
  • Optical Studies of Crazed Plastic Surfaces 1 Sanford B
    Journal of Research of the National Bureau of Standards Vol. 58, No.6, June 1957 Research Paper 2767 Optical Studies of Crazed Plastic Surfaces 1 Sanford B. Newman and Irvin Wolock Opt ical studies were .made of crazed surfaces, p rincipall y t hose of cast poly methyl methacrylate. The techl1lques used for t hese st udies we re mult iple-beam inter fe rometry and li ght and electron m icroscop y. The dil~ e lls i o n s of t he craze cracks prod uced b y short-t ime stress crazing and by stress­ so ~ vent crazmg wcre determmed by t he a bove techniques. Stress-crazed specimens con­ tamed t he sma ll est cracks observed during thi s investigation. The dimensions determined in some of t h e~e specimens were : Le ngth, 2 to. 10 mi crons; wi dth, 0.1 to 0.25 m icron; depth, 0.05 to 0.15 mIcron. I n other speellnens and JJl solvent-crazed surfaces t he dimensions were larger. The craze cracks did not appear to aPjJ roach dimensions unresolvable by the electron m lCroscope, b~ t Instead appeared to have a mll1lmUm crack length. AI: elevatIOn of t he surface in t he vicinity of craze cracks was observed, of the order of 0.02 mI cron ~ or c r ack~ pr?duced by stress-crazing and 0.3 mi cron fo r t hose produced by stress­ solvent crazIng .. Th IS n se was observed in crazed specimens while still under load . The tY PI cal surface dIsplacement was observed in specimens crazed in tension produced by fl ex ure as well as jj] pure tenSIo n, and was observed III polvstyrene and in polymethvl alpha-chloro- acrylate as well as in poly methyl methacrylate.
    [Show full text]
  • Entanglements in Glassy Polymer Crazing: Cross-Links Or Tubes? † ‡ ‡ § Ting Ge,*, Christos Tzoumanekas, Stefanos D
    Article pubs.acs.org/Macromolecules Entanglements in Glassy Polymer Crazing: Cross-Links or Tubes? † ‡ ‡ § Ting Ge,*, Christos Tzoumanekas, Stefanos D. Anogiannakis, Robert S. Hoy,*, ∥ and Mark O. Robbins*, † Department of Chemistry, University of North Carolina, Chapel Hill, North Carolina 27599, United States ‡ Department of Materials Science and Engineering, School of Chemical Engineering, National Technical University of Athens, Athens 15780, Greece § Department of Physics, University of South Florida, Tampa, Florida 33620, United States ∥ Department of Physics and Astronomy, Johns Hopkins University, Baltimore, Maryland 21218, United States ABSTRACT: Models of the mechanical response of glassy polymers commonly assume that entanglements inherited from the melt act like chemical cross-links. The predictions from these network models and the physical picture they are based on are tested by following the evolution of topological constraints in simulations of model polymer glasses. The same behavior is observed for polymers with entanglement lengths Ne that vary by a factor of 3. A prediction for the craze extension ratio Λ based on the network model describes trends with Ne, but polymers do not have the taut configurations it assumes. There is also no evidence of the predicted geometrically necessary entanglement loss. While the number of entanglements remains constant, the identity of the chains forming constraints changes. The same relation between the amount of entanglement exchange and nonaffine displacement of monomers is found for crazing and thermal diffusion in end-constrained melts. In both cases, about 1/ 3 of the constraints change when monomers move by the tube radius. The results show that chains in deformed glassy polymers are constrained by their rheological tubes rather than by entanglements that act like discrete cross-links.
    [Show full text]
  • Distributed Crazing in Rubber-Toughened Polymers
    1 Continuum-micromechanical modeling of 2 distributed crazing in rubber-toughened polymers a b c a1 3 M. Helbig , E. van der Giessen , A.H. Clausen , Th. Seelig a 4 Institute of Mechanics, Karlsruhe Institute of Technology, Kaiserstrasse 12, 76131 Karlsruhe, Germany b 5 Zernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747 AG Groningen, 6 The Netherlands c 7 Structural Impact Laboratory (SIMLab), Department of Structural Engineering, Norwegian University of 8 Science and Technology (NTNU), Rich. Birkelandsvei 1A, NO-7491 Trondheim, Norway 9 Abstract 10 A micromechanics based constitutive model is developed that focuses on the effect 11 of distributed crazing in the overall inelastic deformation behavior of rubber-toughened 12 ABS (acrylonitrile-butadiene-styrene) materials. While ABS is known to exhibit craz- 13 ing and shear yielding as inelastic deformation mechanisms, the present work is meant 14 to complement earlier studies where solely shear yielding was considered. In order to 15 analyse the role of either mechanism separately, we here look at the other extreme and 16 assume that the formation and growth of multiple crazes in the glassy matrix between 17 dispersed rubber particles is the major source of overall inelastic strain. This notion is 18 cast into a homogenized material model that explicitly accounts for the specific (cohesive 19 zone-like) kinematics of craze opening as well as for microstructural parameters such as 20 the volume fraction and size of the rubber particles. Numerical simulations on single- 21 edge-notch-tension (SENT) specimens are performed in order to investigate effects of the 22 microstructure on the overall fracture behavior.
    [Show full text]
  • Crazing As a Method for Preparation of Polymer Blends L
    ISSN 20799780, Review Journal of Chemistry, 2012, Vol. 2, No. 1, pp. 1–19. © Pleiades Publishing, Ltd., 2012. Original Russian Text © L.M. Yarysheva, E.G. Rukhlya, A.Yu. Yarysheva, A.L. Volynskii, N.F. Bakeev, 2012, published in Obzornyi Zhurnal po Khimii, 2012, Vol. 2, No. 1, pp. 3–21. Crazing as a Method for Preparation of Polymer Blends L. M. Yarysheva, E. G. Rukhlya, A. Yu. Yarysheva, A. L. Volynskii, and N. F. Bakeev Department of Chemistry, Moscow State University, Moscow, 119991 Russia email: [email protected], [email protected], [email protected] Received November 29, 2010; in final form, April 6, 2011 Abstract—Publications on the development of a new universal method for the preparation of poly mer–polymer blends are reviewed. This approach is based on the phenomenon of solvent crazing, which comes into play in the tensile drawing of polymers in the presence of adsorptionactive liquid media. It is important that solvent crazing is accompanied by the development of a unique fibillar– porous structure, in which the dimensions of craze pores and fibrils do not exceed several tens of nanometers. Two approaches to the preparation of the polymer–polymer blends are described. According to the first approach, the nanoporous structure of the solventcrazed polymer is filled with the monomer, and its further in situ polymerization results in the polymer–polymer blends. The sec ond approach has been recently advanced by the authors of this publication; it involves direct penetra tion of macromolecules into the formed fibillar–porous structure of the solventcrazed polymer. Both approaches are capable of producing diverse polymeric blends with a high degree of mutual dispersion of the components.
    [Show full text]