Toughening Behaviour of Rubber-Modified Thermoplastic Polymers Involving Very Small Rubber Particles: 1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Fracture of Polycarbonate/Abs Blends
FRACTURE OF POLYCARBONATE/ABS BLENDS PROEFSCHRIFT ter verkrijging van de graad van doctor aan de Universiteit Twente, op gezag van de rector magnificus, prof. dr. F.A. van Vught, volgens besluit van het College voor Promoties in het openbaar te verdedigen op vrijdag 27 april 2001 om 13.15 uur door Judith Pouwlien Frederika Inberg geboren op 27 juli 1972 te Britswerd Dit proefschrift is goedgekeurd door de promotor: Prof. L.C.E. Struik en de assistent-promotor: Dr. R.J. Gaymans ".... Het voornaamste probleem met die Tijdbesparingsobsessie ligt heel eenvoudig: tijd kun je niet besparen. Je kunt hem alleen besteden." Benjamin Hoff, in Tao van Poeh Fracture of polycarbonate/ABS blends J.P.F. Inberg Thesis, University of Twente, Enschede, The Netherlands April 2001 ISBN 90 365 1553x Cover: TEM picture of deformation zone ahead of an arrested crack in a co-continuous polycarbonate/ABS blend Ó J.P.F. Inberg Printed by: Grafisch Centrum Twente, Enschede Voorwoord Met dit proefschrift sluit ik mijn tijd binnen de onderzoeksgroep 'Synthese en Technologie van Engineering Plastics' (STEP) af, en komt er tevens een einde aan mijn tijd in Enschede. Het schrijven van een proefschrift mag dan een wat eenzaam karwei zijn, velen hebben bijgedragen aan het tot stand komen van dit proefschrift, waarvoor allen dank. Een aantal van hen wil ik hier met name noemen. Mijn mentor Reinoud Gaymans, voor het bieden van de mogelijkheid te promoveren binnen een gezellige groep, en de begeleiding van de afgelopen 4 jaar. Mijn promotor Professor Struik, voor de kritische maar altijd bijzonder waardevolle opmerkingen en aanwijzingen. -

Synthesis and Characterization of Liquid Natural Rubber As Impact Modifier for Epoxy Resin
Available online at www.sciencedirect.com ScienceDirect Physics Procedia 55 ( 2014 ) 129 – 137 Eight International Conference on Material Sciences (CSM8-ISM5) Synthesis And Characterization Of Liquid Natural Rubber As Impact Modifier For Epoxy Resin A.B. BEN SALEHa, Z.A. MOHD ISHAKb, A. S. HASHIMb, W.A. KAMILc, U.S. ISHIAKUd Faculty of education, Misurata University,Misurata, Libyaa, School of Material and Mineral Resourcesb School of Chemical Sciencec Universiti Sains Malaysia, Penang, Malaysia Kyoto Institute of Technology, Matsugasaki, Sakyo-kud Kyoto 606-8585, Japan Abstract Liquid natural rubber (LNR) with a molecular weight CMn =16×103 was prepared by the depolymerization of deproteinized natural rubber latex (DPNR). The liquid natural rubber (LNR) was characterized by FTIR and H’NMR spectroscopic analysis. LNR was premixed with the epoxy resin (EP) and cured with a diamine curing agent for 1 h at 100 °C and post cured at 110 °C, for 2 h in air oven. The modified EP containing different contents of LNR (5, 10, 15 and 20 phr) were evaluated. Thermal, mechanical and morphology properties were determined. The fracture toughness (KIC) of both unmodified and modified EPs were determined on static loaded single edge notched (SEN-B) specimens at room temperature. The glass transition temperatures (Tg) of the modified EPs were decreased with increasing LNR content. The strengths and modulus of EPs were slightly reduced with the incorporation of LNR. The effect was also reflected in the significant increase in the tensile strain of modified EP. Fracture toughness of the EP was observed to increase with the presence of LNR. -

Polymer Chemistry Sem-6, Dse-B3 Part-3, Ppt-3
POLYMER CHEMISTRY SEM-6, DSE-B3 PART-3, PPT-3 Dr. Kalyan Kumar Mandal Associate Professor St. Paul’s C. M. College Kolkata Polymer Chemistry Part-3 Contents • Styrene Based Copolymers • Poly(Vinyl Chloride): A Thermoplastic Polymer Styrene Based Copolymers Styrene-Acrylonitrile (SAN) Copolymers and ABS Resins • To obtain a styrene-based polymer of higher impact strength and higher heat distortion temperature at the same time, styrene is copolymerized with 20-30% acrylonitrile. Such copolymers have better chemical and solvent resistance, and much better resistance to stress cracking and crazing while retaining the transparency of the homopolymer at the same time. In many respects SAN copolymers are also better than poly(methyl methacrylate) and cellulose acetate, two other transparent thermoplastics. • ABS resins are terpolymers of acrylonitrile, butadiene and styrene, prepared by interpolymerization (grafting) of styrene and acrylonitrile on polybutadiene or through blending of SAN copolymers with butadiene–acrylonitrile (Nitrile) rubber. Impact improvement is far better if the rubber in the blend is lightly cross-linked. The impact resistance of ABS resins may be as high as 6-7 ft lb. per inch of notch. This Lecture is prepared by Dr. K. K. Mandal, SPCMC, Kolkata Styrene-Acrylonitrile (SAN) Copolymers • Styrene acrylonitrile resin is a copolymer plastic consisting of styrene (Ph-CH=CH2) and acrylonitrile (CH2=CH-CN). It is also known as SAN. It is widely used in place of polystyrene owing to its greater thermal resistance. • The chains of between 70 and 80% by weight styrene and 20 to 30% acrylonitrile. Larger acrylonitrile content improves mechanical properties and chemical resistance, but also adds a yellow tint to the normally transparent plastic. -

Fatigue Craze Initiation in Polycarbonate: Study by Transmission Electron Microscopy
Fatigue craze initiation in polycarbonate: study by transmission electron microscopy Hristo A. Hristov, Albert F. Yee* and David W. Gidleyt Department of Materials Science and Engineering and tDepartment of Physics, University of Michigan, Ann Arbor, MI 48109, USA (Received 22 October 1993; revised 26 January 1994) Fatigue craze initiation in bulk, amorphous polycarbonate (PC) is investigated by means of transmission electron microscopy. The results agree very well with small angle X-ray scattering measurements of the same set of samples, and confirm that void generation is the main characteristic of the initiation process. The evolution of the initial void-like structures or 'protocrazes' with dimensions of ~ 50 nm into crazes with dimensions of several micrometres is presented in considerable detail. It is found that some similarities exist between crazes induced by cyclic fatigue at room temperature and crazes produced in monotonic loading at temperatures close to the glass transition. The similarities suggest that disentanglement of polymer chains plays an important role in the fatigue craze initiation process in bulk, amorphous PC near room temperature. (Keywords: fatigue; craze initiation; polycarbonate) INTRODUCTION describing fatigue craze initiation have not been The importance of crazing in the structural integrity of developed either (reviews of the existing models of craze polymeric materials under load was recognized more initiation under constant load can be found in references than 20 years ago, which prompted the beginning of 9 and 16). It seems that optical microscopy (conventional systematic investigations of structure of crazes in and interference optical microscopy) is the most polymers by, among other techniques, transmission frequently used method for studying the gross structure electron microscopy (TEM) 1-4. -

The Growth of Cracks and Crazes in Polymers
THE GROWTH OF CRACKS AND CRAZES IN POLYMERS - A FRACTURE MECHANICS APPROACH GEORGE PHILIP MARSHALL MARCH W72 A thesis submitted for the degree of Doctor of Philosophy of the University of London and for the Diploma of Imperial College. Department of Mechanical Engineering Imperial College, . London S.W.7. ABSTRACT A study has been made of the use of fracture mechanics in describing crack and craze growth phenomena in plastics. The thesis which follows has been divided into three main parts. Part I has two component chapters. The first (Ch. 2)/ outlines the basis of the fracture mechanics concepts used in the analysis of results and the second chapter (Ch. 3) contains a literature survey of the state of knowledge on crazing and environmental stress cracking in plastics. Part II describes experimental work which has been undertaken to study crack growth phenomena in both air and liquid environments. Chapter 4 gives results obtained from slow crack propagation tests in PMMA in air and shows that there is a unique relationship between the fracture toughness measure Kc and the crack speed. Analysing results on a /crack speed basis is shown to ration- alise results from many different types of test and also accounts for the rate dependent material characteristics. This approach is extended in Chapter 5 to include the effects of crack propagation in polystyrene in air. For the first time, realistic values of fracture toughness have been obtained for the propaga- tion of a single crack/craze system. The Kc vs crack speed relationship is again found to provide a good basis against which results may be compared and dis- cussed. -

And Micromechanics of Polymers
Sample Pages Goerg H. Michler, Francisco J. Baltá-Calleja Nano- and Micromechanics of Polymers Structure Modification and Improvement of Properties ISBN: 978-3-446-42767-9 For further information and order see http://www.hanser.de/978-3-446-42767-9 or contact your bookseller. © Carl Hanser Verlag, München 4 4 Crazing 4.1 The Phenomenon of „Craze“ As mentioned in the previous chapter, plastic deformation of polymers is a heterogeneous process, concentrated in local zones. Local plastic processes appear in form of shear bands, void formation with fibrillation, inter- and intra- spherulitic deformation, and formation of crazes. Crazing has been inten sively investigated over the last 60 years, with major reviews appearing regularly [1−8]. It is usually assumed that crazes are typical of amorphous, glassy polymers, such as PS, SAN, and PMMA, which are brittle at room temperature with elongation at break of a few percent. The reason is that crazes are visible in the amorphous, glassy polymers during mechanical loading with the eye in reflected light (see Fig. 4.1). Their macroscopic appearance of cracks left these zones with the name of craze. “Craze” is an old English word for hairline crack. Synonyms include “craquele” (from the pattern of cracks in the glaze of porcelain (china) or pottery, microcracks and “silver cracks” (from the Russian name). FIGURE 4.1 Tensile bars after loading in overview (left) and low optical magnifications of the bars (right); a) polystyrene; b) poly(methylmethacrylate) 120 4 Crazing Several crack-like zones The formation of crack-like zones in brittle materials under stress is a very general phenomenon, which is observed in very different materials: Inorganic glasses are typical examples of amorphous brittle materials with very fast crack propagation. -
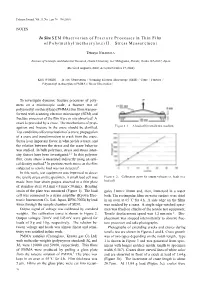
In Situ SEM Observation of Fracture Processes in Thin Film of Poly(Methyl Methacrylate) II
Polymer Journal, Vol.35, No. 1, pp 76—78 (2003) NOTES In Situ SEM Observation of Fracture Processes in Thin Film of Poly(methyl methacrylate) II. Stress Measurement Tetsuya NISHIURA Institute of Scientific and Industrial Research, Osaka University, 8–1 Mihogaoka, Ibaraki, Osaka 567–0047, Japan (Received August 6, 2002; Accepted October 17, 2002) KEY WORDS In situ Observation / Scanning Electron Microscope (SEM) / Craze / Fracture / Poly(methyl methacrylate) (PMMA) / Stress Observation / To investigate dynamic fracture processes of poly- mers on a microscopic scale, a fracture test of poly(methyl methacrylate) (PMMA) thin films was per- formed with scanning electron microscope (SEM) and fracture processes of the film were in situ observed.1 A crack is preceded by a craze. The mechanisms of prop- agation and fracture in the craze should be clarified. Figure 1. A load cell in tensile test machine. Test conditions affect nucleation of a craze, propagation of a craze and transformation to crack from the craze. Stress is an important factor in what yields a craze, and the relation between the stress and the craze behavior was studied. In bulk polymers, stress and stress inten- sity factors have been investigated.2, 3 In thin polymer film, craze stress is measured indirectly using an opti- cal density method.4 In previous work stress on the film subjected to tensile load was not detected.1 In this work, test equipment was improved to detect the tensile stress on the specimen. A small load cell was Figure 2. Calibration curve for output voltages vs. loads in a made from four strain gauges attached to a thin plate load cell. -

Fracture Toughness of Polypropylene-Based Particulate Composites
Materials 2009, 2, 2046-2094; doi:10.3390/ma2042046 OPEN ACCESS materials ISSN 1996-1944 www.mdpi.com/journal/materials Review Fracture Toughness of Polypropylene-Based Particulate Composites David Arencón and José Ignacio Velasco * Centre Català del Plàstic, Universitat Politècnica de Catalunya, Edifici Vapor Universitari, Colom 114, 08222, Terrassa, Spain; E-Mail: [email protected] (D.A.) * Author to whom correspondence should be addressed; E-Mail: [email protected] (J.I.V.); Tel.: +34 937 837 022; Fax: +34 937 841 827. Received: 27 October 2009; in revised form: 24 November 2009 / Accepted: 27 November 2009 / Published: 30 November 2009 Abstract: The fracture behaviour of polymers is strongly affected by the addition of rigid particles. Several features of the particles have a decisive influence on the values of the fracture toughness: shape and size, chemical nature, surface nature, concentration by volume, and orientation. Among those of thermoplastic matrix, polypropylene (PP) composites are the most industrially employed for many different application fields. Here, a review on the fracture behaviour of PP-based particulate composites is carried out, considering the basic topics and experimental techniques of Fracture Mechanics, the mechanisms of deformation and fracture, and values of fracture toughness for different PP composites prepared with different particle scale size, either micrometric or nanometric. Keywords: polypropylene; composites; fracture toughness 1. Introduction Particulate filled polymers are used in very large quantities in all kinds of applications and despite the overwhelming interest in advanced composite materials, considerable research and development is done on particulate filled polymers even today. Fillers increase stiffness and heat deflection temperatures, decrease shrinkage and improve the appearance of composites [1–3]. -

Multiscale Behavior of Fused Deposition Additively Manufactured Thermoplastic Cellular Materials Kaitlynn Melissa Conway Clemson University, [email protected]
Clemson University TigerPrints All Theses Theses 8-2018 Multiscale Behavior of Fused Deposition Additively Manufactured Thermoplastic Cellular Materials Kaitlynn Melissa Conway Clemson University, [email protected] Follow this and additional works at: https://tigerprints.clemson.edu/all_theses Recommended Citation Conway, Kaitlynn Melissa, "Multiscale Behavior of Fused Deposition Additively Manufactured Thermoplastic Cellular Materials" (2018). All Theses. 2954. https://tigerprints.clemson.edu/all_theses/2954 This Thesis is brought to you for free and open access by the Theses at TigerPrints. It has been accepted for inclusion in All Theses by an authorized administrator of TigerPrints. For more information, please contact [email protected]. MULTISCALE BEHAVIOR OF FUSED DEPOSITION ADDITIVELY MANUFACTURED THERMOPLASTIC CELLULAR MATERIALS A Thesis Presented to the Graduate School of Clemson University In Partial Fulfillment of the Requirements for the Degree Master of Science Mechanical Engineering by Kaitlynn Melissa Conway August 2018 Accepted by: Dr. Garrett J. Pataky: Thesis Advisor, Committee Chair Dr. Joshua D. Summers Dr. Huijuan Zhao Abstract Cellular materials are known for being lightweight as well as deforming in unique ways. Cellular materials have become more viable due to additive manufacturing (AM). AM cellular materials are easier to fabricate compared to traditional cellular materials and AM cellular materials are not as limited in geometry as traditional fabrication methods were. AM materials were studied in this paper in a two-phase approach. Phase 1 focused on the global mechanical properties of AM cellular materials. Phase 2 focused on the crazing of AM thermoplastic glassy polymers and how additive manufacturing affects the behavior or cellular materials. Because cellular materials do not have a consistent cross sectional area throughout the material, there is not a standard cross sectional area to use for property calculations. -

Craze Initiation in Glassy Polymer Systems
Craze initiation in glassy polymer systems MT02.002 O.F.J.T Bressers Master report Supervisors: dr. ir. J.M.J. den Toonder Philips Research ir. H.G.H. van Melick TU/e dr. ir. L.E. Govaert TU/e prof. dr. ir. H.E.H. Meijer TU/e Summary This report deals with the numerical simulation of craze initiation in amorphous polymer systems. The approach is based on the view that the development of a craze is preceded by de formation of a localised plastic deformation zone. As this zone develops, the hydrostatic stress increases, and, when exceeding a critical stress level, cavitation will take place leading to local development of voids. The voids grow, coalesce and the ligaments between the voids are subsequently super-drawn leading to the typical structure of a craze: a crack-like defect bridged by highly drawn filaments. In Part 1 a critical hydrostatic stress is examined as a cavitation criterion for polymers in a well-defined experiment. A micro indenter with a 150 m sapphire sphere produces reproducible indents, which are later examined with an optical microscope. These observations lead to a critical force where crazes are initiated in polystyrene (PS). Combination of these experiments with a numerical study using the compressible Leonov-model showed that the loading part of the indentation can be accurately predicted. A critical hydrostatic stress of 39MPa is extracted from the numerical model by analysis of the local stress field at the moment the indentation force reaches the experimentally determined force level at which crazes were found to initiate. -

Chapter 3 Rubber Elasticity
Chapter 23 Fracture and Toughening Fracture behavior Fracture testing Impact/Fatigue Toughening Failure or fracture Ch 23 sl 2 failure [破碎, 破斷] ~ rupture by exceedingly large stress fracture [破壞] ~ failure by crack propagation micromechanism of fracture Fig 23.4 p561 chain scission or slip? radical conc’n by ESR Upon stress, 1. chain slip (against Xtal, Xlinking, entangle) higher than ey 2a. crazing/yielding or lower than ef 2b. chain scission (early) when high Xc, low Mc, low Me 3. then chain scission 4. voiding crack fracture effect of MM (on strength) Fig 23.5 M = 6 – 8 Me? MM should be much higher than Me. Brittle fracture Ch 23 sl 3 theoretical (tensile) strength of solids (by Griffith) for interatomic separation pp557-558 st = tensile strength whiskers, su or sf ≈ E/10 su = ultimate stress sf = fracture stress polymer single crystals, su or sf ≈ E/40 sc = craze stress for (isotropic glassy unfilled) polymers, su = sf = sc if brittle sf < E/100 < stheo E = 1 – 3 GPa, sf < 100 MPa due to flaw [crack, notch, or inclusion], which cause stress concentration and plastic constraint Ch 23 sl 4 stress concentration Ahead of crack tip, stress is larger than the applied stress s0 s0 circular crack [a=b], s = 3 s0 crack-tip radius Fig 23.6 p562 Fracture mechanics Ch 23 sl 5 energy balance approach LEFM [linear elastic FM] specimen with crack length 2a Crack grows when released (elastic) strain energy by stress [s2pa2/2E] is greater than created surface energy [4ag] Griffith (brittle) fracture criterion plane s plane -

Toughening of Epoxy Resin Using Natural And
TOUGHENING OF EPOXY RESIN WITH MODIFIED LIQUID NATURAL RUBBERS AND ACRYLONITRILE-BUTADIENE LIQUID RUBBERS By ABDULALI BASHIR AHMED BEN SALEH Thesis submitted in fulfilment of the requirements for the degree of doctor of philosophy September 2005 [96:1-5] Read! In the name of your Lord who created - Created the human from something which clings. Read! And your Lord is Most Bountiful - He who taught (the use of) the Pen, Taught the human that which he knew not. Chapter 96: AL-ALAQ Acknowledgements By the name of Allah the beneficent and the merciful, all praise and thanks is due to Allah the indivisible creator and sustainer of the world, he can never be praised or thanked enough. I would like to extend my sincere gratitude to my big family (my parents, brothers and sisters) for their support, dedication and advice. Not forgetting my small family (my wife and daughters) who had constantly given me healthy weather in all aspects of my life study. I would like to thank my supervisors, Prof. Dr. Zainal Arifin .Mohmed Ishak, Associate Prof. Dr. Azanam Shah Hashim and Associate Prof. Dr. Wan Ahmed Kamil for their continuing support & mentorship in my study. The assistance of Prof. Dr. Umaru S. Ishiaku at the earlier stages of my research is also acknowledged. Acknowledgements are also due to staff and laboratory technician, School of Materials and Mineral Resource Engineering. My respect and thanks are due to all staff and laboratory technician, School of Chemical Science, Universiti Sains Malaysia for their tireless help and cooperation during my research. I would also like to extend my grateful appreciation and thanks to my colleagues, classmates and friends, for their friendship and support and all postgraduate students of polymer department are also acknowledged.