Hong Kong Hospital Authority Resource Efficiency Evaluation: Via a Novel DEA- Malmquist Model and Tobit Regression Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

E-Newsletter
E-Newsletter INAUGURATION ISSUE 2016 With the support of The Hong Kong Jockey Club Charities Trust, a three-year initiative, Jockey Club End-of-Life Community Care (JCECC) Project, was launched in 2015. The project aims at improving the quality of end-of-life care, enhancing the capacity of service providers and raising public awareness. FEATURE On February 25, 2016, The JCECC Project, together with Hospital Authority and Hong Kong Society of Palliative Medicine, organised a Symposium on Collaboration and Communications in Health and Social Care for End-of-Life Care. The Symposium featured three knowledgeable speakers including Professor Ilora Finlay from University of Cardiff, Mr. Richard Yuen from Food and Health Bureau and Professor Cecilia Chan from the JCECC Project. In Hong Kong, the proportion of deaths of people aged 65 or over has increased from 67.2% (in 1991) to 78.4% (in 2011), amounting to a 73% increase in actual deaths. In the same period, the overall number of deaths also increased; therefore, the demand for end-of-life care has grown tremendously. Despite that, the development of end-of-life care in Hong Kong has been below average. In the 2015 Quality of Death Index, Hong Kong was ranked only 22nd out of 80 regions, behind other developed Asian regions like Taiwan, Singapore, Japan and South Korea. The United Kingdom ranked 1st in the index and there are a lot of experience that can be learnt from the UK on end-of-life care in terms of systems, infrastructures and community education. Professor Finlay, The Baroness Finlay of Llandaff and Professor of Palliative Medicine in Cardiff University, with Mr. -
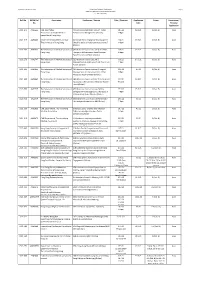
From 1.1.2021 Onwards
Updated as of 30 June 2021 Hong Kong College of Radiologists Page 1 CME/ CPD Application (Association/Personal) 1.1.2021-30.6.2021 Ref. No. HKAM Ref. Association Conference / Lecture Date / Duration Application Points Association / No. Date Personal Application 2021-475 AA02635 CME Committee "It's not COPD, but Heart Failure" - From 18.5.21 19.4.21 1 (Cat. B) Asso Association of Private Medical Prevention to Management (Online) 7-8pm Specialists of Hong Kong 2021-319 AA02466 Centre for Medical Ethics and Law (Webinar) Gross Negligence Manslaughter: 9.4.21 10.3.21 2 (Cat. B) Asso The University of Hong Kong Should it apply to healthcare practitioners? 4-6pm (Online) 2021-463 AA02611 The Federation of Medical Societies of [IBD Intensive Course Lecture 3] Anti-TNF 4.5.21 13.4.21 1 (Cat. B) Asso Hong Kong Therapy in Inflammatory Bowel Disease: 8-9pm Past, Present and Future (Online) 2021-579 AA02747 The Federation of Medical Societies of [IBD Intensive Course Lecture 5] 8.6.21 17.5.21 1 (Cat. B) Asso Hong Kong Management of Acute Severe UC: Pearls and 7-8pm Pitfalls (Online) 2021-635 AA02805 The Federation of Medical Societies of [IBD Intensive Course Lecture 6] Surgical 22.6.21 4.6.21 1 (Cat. B) Asso Hong Kong Management of Ulcerative Colitis: What 7-8pm Physicians Need to Know (Online) 2021-685 AA02867 The Federation of Medical Societies of [IBD Intensive Course Lecture 7] Perianal and 13.7.21 16.6.21 1 (Cat. B) Asso Hong Kong Fistulizing Crohn’s Disease: How Do I Tackle 9-10pm Them (Online) 2021-380 AA02529 The Federation of Medical Societies of [IBD Intensive Course: Lecture 2] Non- 23.4.21 25.3.21 1 (Cat. -

Report of the Steering Committee on Review of Hospital Authority
Report of the Steering Committee on Review of Hospital Authority July 2015 CONTENTS Glossary .................................................................................................................. iii Executive Summary ................................................................................................ v Chapter 1 Introduction ...................................................................................... 1 Chapter 2 Work of the Steering Committee ...................................................... 6 Chapter 3 Major Challenges Facing the Hospital Authority ............................ 9 Chapter 4 Management and Organisation Structure ....................................... 13 Chapter 5 Resource Management ................................................................... 26 Chapter 6 Staff Management .......................................................................... 42 Chapter 7 Cost Effectiveness and Service Management ................................ 59 Chapter 8 Overall Management and Control .................................................. 87 Chapter 9 Conclusion ...................................................................................... 96 Annex 1 Membership of the Steering Committee on Review of Hospital Authority ....................................................................................... 102 Annex 2 Report of the Public Engagement Programme ............................. 103 Annex 3 Clustering of Hospitals and Institutions ...................................... -

List of Flights/Trains/Ships/Vehicles Taken by Confirmed Or Probable Cases of COVID-19 from 2 Days Before Onset of Symptoms
List of flights/trains/ships/vehicles taken by confirmed or probable cases of COVID-19 from 2 days before onset of symptoms (Note: The flights/trains/ships/vehicles will remain on the list for 14 days since the last date of travel by the cases) Flight/Train/ Departure & arrival Date of travel Related Ship number probable/confirmed cases Diamond Yokohama, Japan → Hong Kong Since Case 14, 71, 78, 79, Princess → Yokohama, Japan 20/01/2020 80, 81, 87, 88, 94, 96, 97 and an outbreak reported by the health authority of Japan Taxi 1. Block 3, Grand Yoho→Pok Oi 21/02/2020 Case 75 Hospital 2. Pok Oi Hospital→Block 3, Grand Yoho Taxi Fly Dragon Terrace, 26-32 Tin 22/02/2020 Case 70 Hau Temple Road→Pamela Youde Nethersole Eastern Hospital Taxi Maylun Apartments, 1-25 Shu 22/02/2020 Case 74 Kuk Street→Pamela Youde Nethersole Eastern Hospital Flight CX694 New Delhi→Hong Kong 24/02/2020 Case 105 Taxi HK station→Villa Lotto 24/02/2020 Case 105 Flight CX250 London→Hong Kong 28/02/2020 Case notified by (Arrival in Health Commission of Hong Kong) Guangdong Province Ferry 3A109 SkyPier→Shekou 28/02/2020 Case notified by Health Commission of Guangdong Province Flight CX250 London→Hong Kong 29/02/2020 Case notified by the health authority of Thailand Flight CX617 Hong Kong→Bangkok 29/02/2020 Case notified by the health authority of Thailand Flight CX838 Hong Kong→Vancouver 29/02/2020 Case 105 related contact tracing Taxi 1. Villa Lotto→Tang Shiu Kin 02/03/2020 Case 105 Hospital 2. -
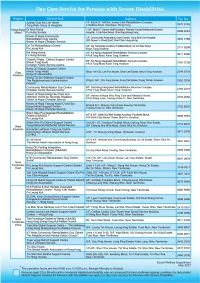
List of Service Units of DC SD (Eng)
- A •• Address Jockey Club Kin Lok Home 1/F, Block D, TWGHs Jockey Club Rehabilitation Complex, Tung Wah Group of Hospitals 4 Welfare Road, Aberdeen, Hong Kong 2870 9153 Oi Wah Home 1-2/F, Block F, Senior Staff Quarters, Pamela Youde Nethersole Eastern Hong Kong 2896 2543 Island Fu Hong Society Hospital, 3 Lok Man Road, Chai Wan,Hong Kong Haven of Hope Community Rehabilitation Day Centre 1/F, Community Ambulatory Care Centre, Tang Shiu Kin Hospital, 3553 3188 282 Queen ' s Road East, Wan Chai, Hong Kong Haven of Hope Christian Service On Tai Rehabilitation Centre 4/F, On Tai Estate Ancillary Facilities Block, 23 On Sau Road, 2711 9299 Po Leung Kuk K1NUn Tong, Kowloon Kai Hong Home 2/F, Kai Nang Integrated Rehabilitation Services Complex, 3611 6406 Fu Hong Society 4 Fuk Tong Road, Kwun Tong, Kowloon Cheerful Place - District Support Centre 8/F, Kai Nang Integrated Rehabilitation Services Complex, (Kwun Tong East) 2191 3138 Christian Family Service Centre 4 Fuk Tong Road , Kwun Tong , Kowloon Hong Chi District Support Centre (Kwun Tong West) East Shop 116-123, Lee Foo House, Shun Lee Estate, Kwun Tong, Kowloon 2344 9724 Kowloon Hong Chi Association Wong Tai Sin Wellness Support Centre The Neighbourhood Advice-Action Wing A, G/F., Chu Fung House, Fung Tak Estate, Wong Tai Sin, Kowloon 2320 7834 Council Community Rehabilitation Day Centre 8/F, Kai Nang Integrated Rehabilitation Services Complex, Christian Family Service Centre 4 Fuk Tong Road, Kwun Tong , Kowloon 2793 2218 Haven of Hope Hang Hau Care and Attention Home for Severely Disabled -

Item for Public Works Subcommittee of Finance Committee
For discussion PWSC(2002-03)5 on 3 April 2002 ITEM FOR PUBLIC WORKS SUBCOMMITTEE OF FINANCE COMMITTEE HEAD 708 – CAPITAL SUBVENTIONS AND MAJOR SYSTEMS AND EQUIPMENT Medical Subventions 47MM – Remodelling of Tang Shiu Kin Hospital into an ambulatory care centre Members are invited to recommend to Finance Committee the upgrading of 47MM to Category A at an estimated cost of $239.1 million in money-of-the- day prices for the remodelling of Tang Shiu Kin Hospital into an ambulatory care centre. PROBLEM We need to cope with the escalating demand for medical services in the Hong Kong East cluster1. The provision of ambulatory care services in the Causeway Bay - Wan Chai District is scattered over various locations and is far from being efficient in the delivery of health care services. /PROPOSAL ….. __________________________________________________________________ 1 At present, HA provides medical services for the community through eight hospital clusters. Each hospital cluster comprises a number of acute and convalescent/rehabilitation hospitals and institutions, providing a full range of comprehensive health care services to meet the health care needs of the community. The medical services for Wan Chai and Eastern districts are provided by the Hong Kong East hospital cluster which comprises Ruttonjee and Tang Shiu Kin Hospitals, Tung Wah Eastern Hospital, Wong Chuk Hang Hospital, Pamela Youde Nethersole Eastern Hospital, Cheshire Home (Chung Hom Kok), St John Hospital, Tang Chi Ngong Specialist Clinic and facilities in Southorn Centre. PWSC(2002-03)5 Page 2 PROPOSAL 2. The Director of Architectural Services (D Arch S), with the support of the Secretary for Health and Welfare, proposes to upgrade 47MM to Category A at an estimated cost of $239.1 million in money-of-the-day (MOD) prices to remodel Tang Shiu Kin Hospital (TSKH) into an ambulatory care centre. -

2006 Annual Report on JP Visits
2006 Annual Report on JP Visits Administration Wing of the Chief Secretary for Administration’s Office 2006 Annual Report on JP Visits Introduction This Annual Report, the eighth of its kind, covers the work of Justices of the Peace (JPs) in the calendar year 2006 in visiting designated institutions, handling complaints from prisoners and inmates, and making suggestions and comments to institutions. The JP System 2. The operation of the JP system is underpinned by the Justices of the Peace Ordinance (the Ordinance) (Cap. 510) which provides for the appointment, functions, resignation and removal of JPs. JPs are appointed by the Chief Executive under section 3(1) of the Ordinance. For administrative purpose, JPs appointed by virtue of their holding of certain offices in the public service are often referred to as Official JPs while others as Non-official JPs. Functions of JPs 3. The main functions of JPs, as provided for in section 5 of the Ordinance, are as follows - (a) to visit custodial institutions and detained persons; (b) to take and receive declarations and to perform any other functions under the Oaths and Declarations Ordinance (Cap. 11); (c) in the case of a Non-official JP, to serve as a member of any advisory panel; and (d) to perform such other functions as may be imposed on him/her from time to time by the Chief Executive. 4. The primary role of a JP is to visit institutions, such as prisons, detention centres, hospitals and remand/probation homes, with a view to ensuring that the rights of the inmates are safeguarded through a system of regular visits by independent visitors. -

A General Brief About the Hospital Authority
Mission Statement 4. In keeping with its role, the Mission of the Hospital Authority is: · to meet the different needs of patients for public hospital services, and to improve the hospital environment for the benefit of patients; · to serve the public with care, dedication and efficiency, and to encourage community participation in the system, resulting in better care and more direct accountability to the public; · to provide rewarding, fair and challenging employment to all its staff, in an environment conducive to attracting, motivating and retaining well-qualified staff; · to advise the Government of the needs of the community for public hospital services and of the resources required to meet these needs, in order to provide adequate, efficient, effective and value for money public hospital services of the highest standards recognised internationally within the resources obtainable; and · to collaborate with other agencies and bodies in the healthcare and related fields both locally and overseas to provide the greatest benefit to the local community. Corporate Vision and Strategies 5. To realise its mission, the Hospital Authority has developed the following Corporate Vision: “The Hospital Authority will collaborate with other healthcare providers and carers in the community to create a seamless healthcare environment which will maximise healthcare benefits and meet community expectations.” 6. The Authority achieves this corporate vision by formulating a set of strategic directions every year through an extensive annual planning process, taking into account the funding position, societal expectations, Government’s healthcare policy, and the challenges in the internal and external environment. The 2 corporate vision and mission are turned into operational targets to meet the community needs for healthcare services. -

C.V. of Dr. Andrew K.W. SO Postal Address: P.O
Research Engineering Development Facade Consultants Limited 雄略幕牆顧問有限公司 Tel: 2807-0930 Fax: 2662-6105 C.V. of Dr. Andrew K.W. SO Postal Address: P.O. Box 288 Tuen Mun Central Post Office, N.T., HONG KONG Tel. No.: 2807-0930 Fax No.: 2662-6105 Mobile: 9041-7821 1. PERSONAL PARTICULARS Present Position: Director Research Engineering Development Facade Consultants Ltd. Co-chairman of Façade Group of HKISC 2. QUALIFICATIONS 09/2008 Registered Professional Engineer (Fire) Engineers Registration Board 01/2007 Fellow member and Certified Laboratory The Hong Kong Institution of Certified Manager Auditors 11/2006 MHKIE (Fire Discipline) The Hong Kong Institution Engineers 11/2000 Fellow member Hong Kong Institute of Steel Construction 11/1995 Doctor of Philosophy in Civil Engineering The Hong Kong Polytechnic University 11/1991 Master of Philosophy in Civil Engineering Hong Kong Polytechnic, HK 11/1989 B.Eng. (Hons.) in Civil Engineering Hong Kong Polytechnic, HK 3. COMMUNITY SERVICES Working Group on the Structural Use of Glass (PNAP APP-37, PNAP APP-110), Buildings Department , Hong Kong(2011). Member of the Sub-committee on Review of the Use of Glass in Building Works (PNAP), Buildings Department, HONG KONG(2006). 4. PAST PROJECTS IN CONSULTANCIES AND TESTING Fire Testing Fire resistance tests for specimens including Timber Fire Doors, Steel Fire Doors, Roller Shutters, Glazed Screen Walls, Windows, Curtain Walls, Cement Sand Grout, GRC partitions, Glazed Doors and Other Special Joint Design. Fire performance test for building materials. Examples -

Demand for Accident and Emergency Services During Public Holidays
Legislative Council Secretariat IN 1 / 96-97 INFORMATION NOTE Demand for Accident and Emergency Services During Public Holidays Demand in 1992-96 1. There are 14 public hospitals1 in Hong Kong offering free Accident and Emergency 2 (A & E ) all the year round. Table 1 and Figure 1 show that the demand for A & E services has been growing in the past five years. Table 1:Total A&E Attendance 1992 - 1996 Fig. 1 - Total No. of A & E Attendance, 92-96 ( '000) 92/93 93/94 94/95 95/96 2000 Total No. of 1800 A & E 1,378,181 1,466,482 1,716,559 1,960,001 attendance 1600 Change in % 1400 over the n.a. 6.41% 17.05% 14.18% 1200 previous year 92/93 93/94 94/95 95/96 n.a. = not available Source of Table 1 and Fig. 1 : Hospital Authority Demand During Public Holidays 2. During public or extended holidays, the number of A & E attendance is higher. Figs. 2 to 5 show the average number of A & E attendance per hospital during different public holidays and normal periods. The figures illustrate that on average, A & E attendance during public holidays is 13% higher than that of a normal day. Fig.2 - Average A&E Attendance Per Hospital during Fig. 3 - Average A&E Attendance Per Hospital during Christmas, 95 Chinese New Year, 96 440 510 420 470 Ave. A&E 400 Ave. A&E 430 attendance, 1-21 Feb. 96 380 Attendance, No. of Attendance 1-26 Dec. 95 390 No. -

Hospital Authority's Planned Projects for 2021-2022
LC Paper No. CB(4)503/20-21(02) Head 708 Subhead 8083MM One-Off Grant to the Hospital Authority for Minor Works Projects 2021-22 Planned Projects Prepared by the Hospital Authority February 2021 Head 708 : Subhead 8083MM One-off Grant to the Hospital Authority for Minor Works Projects for the 2019-20 Financial Year Part A - Previously approved items and other items to commence in 2020-21 with expected expenditure in 2020-21 and/or 2021-22 Actual Approved Cumulative Revised Estimated cash flow in subsequent years Expenditure Estimate Priority / Project Expenditure Estimate Project Title (1.4.2020 to 2021-22 Post Item No. Estimate to 31.3.2020 2020-21 31.10.2020) 2022-23 2023-24 2024-25 2024-25 ($'000) (I) Previously approved items (up to 31.10.2020) with expected expenditure in 2020-21 and/or 2021-22 EMR15-604 Modernisation of lifts in Day Treatment Block and Special Block in Prince of Wales Hospital 16,794 16,540 254 254 - - - - - EMR16-104 Replacement of the local central control and monitoring system for Wong Chuk Hang Hospital 1,280 1,150 39 101 - 30 - - - EMR16-401 Replacement of fire alarm and detection system at Hospital Main Block in Tseung Kwan O 6,500 6,500 (1,371) (1,371) - - - - - Hospital EMR16-504 Replacement of 1 no. main switch board for Block A in Yan Chai Hospital 2,345 2,202 142 142 - - - - - EMR16-505 Replacement of building management system at Multi Services Complex in Yan Chai Hospital 3,500 3,148 55 55 297 - - - - EMR16-506 Replacement of the air handling unit for Department of Central Supporting Services at 1/F, 502 526 (24) (24) - - - - - Block B in Yan Chai Hospital EMR17-102 Replacement of emergency generators for Hospital Block at St. -

Primary Care Development Strategy
LC Paper No. CB(2)1995/09-10(01) For information on 12 July 2010 Legislative Council Panel on Health Services Healthcare Service Reform – Primary Care Development Strategy PURPOSE This paper briefs Members on the latest progress of the primary care development strategy formulated based on the advice and recommendations of the Working Group on Primary Care (WGPC). BACKGROUND 2. Enhancing primary care is one of the proposals put forward in the Healthcare Reform Consultation Document “Your Health, Your Life” and received broad public support during the first stage public consultation conducted in March to June 2008. In recognition of the broad support, the Chief Executive announced in the 2008-09 Policy Address that the Government would allocate resources to implement this proposal, and the Secretary for Food and Health would set up the WGPC to take forward the initiative. 3. To this end, WGPC was reconvened under the Health and Medical Development Advisory Committee (HMDAC) in October 2008, involving medical professionals from both the public and private sectors, academia, patient groups and other stakeholders, to discuss and provide strategic recommendations on enhancing and developing primary care in Hong Kong. Three Task Forces were set up under WGPC to study specific proposals set out in the healthcare reform consultation document, taking into account the views collected during the first stage public consultation on healthcare reform. PRIMARY CARE DEVELOPMENT STRATEGY WGPC Initial Recommendations 4. After extensive deliberations at