Geometry Basic Definitions

Total Page：16

File Type：pdf, Size：1020Kb

Geometry Basic Definitions All definitions must be written in “If ... then ...” form in An angle is made up of two rays (sides) with a common endpoint (vertex). An acute angle is an angle whose measure is greater than 0° and less than 90°. A right angle is an angle whose measure is 90°. An obtuse angle is an angle whose measure is greater than 90° and less than 180°. A straight angle is an angle whose measure is 180°. ≅ Congruent angles are angles that have the same measure. ≅ Congruent segments are segments that have the same length. Points that lie on the same line are called collinear. A theorem is a mathematical statement that can be proved. The midpoint of a segment is a point that divides the segment into two congruent M segments. A point (or segment, ray or line) that divides a segment into two congruent segments M bisects the segment. Two points (segments, rays or lines) that divide a segment into three congruent A B segments trisect the segment. The two points at which the segment is divided are called the trisection points of the segment. The bisector of an angle is a ray that divides the angle into two congruent angles. (The ray is said to bisect the angle ) Two rays that divide an angle into three congruent angles trisect the angle. The two dividing rays are called trisectors of the angle. A postulate is an unproved assumption. A definition states the meaning of a term or idea. Union: The set of all elements contained in two sets. ∪ Intersection: The set of all elements common to two set. ∩ Empty Set: The set containing no elements. ∅ Betweenness: If a point is between two other points, then the three points are collinear and the sum of the measures of the smaller segments formed by the three points is equal to the measure of the longest segment. (A-B-C ⇒ AB + BC = AC) Triangle Inequality: If three points are non-collinear, then the sum of the lengths of any two sides is greater than the length of the third side. (AB + BC > AC, BC + AC > AB, and AC + AB > BC) Angle Addition: If two angles are adjacent angles then the sum of the measures of the two smaller angles is equal to the measure of the larger angle. (If X is in the interior of ∠PAQ, then m∠PAQ = m∠PAX + m∠XAQ) Probability: Probability = number of winners number of possibilities Theorems: If two angles are right angles, then they are congruent. If two angles are straight angles, then they are congruent. Postulate: Two points determine a line. Logic and Reasoning: Conditional sentence: p ⇒ q Converse: q ⇒ p Inverse: ∼p ⇒ ∼q Contrapositive: ∼q ⇒ ∼p If a conditional sentence is true then the contrapositive is true. Chain of reasoning: If p ⇒ q and q ⇒ r, then p ⇒ r Also: A complete rotation about a point is 360° .

Copy Link

Recommended publications

Lecture 3 1 Geometry of Linear Programs
ORIE 6300 Mathematical Programming I September 2, 2014 Lecture 3 Lecturer: David P. Williamson Scribe: Divya Singhvi Last time we discussed how to take dual of an LP in two different ways. Today we will talk about the geometry of linear programs. 1 Geometry of Linear Programs First we need some definitions. Definition 1 A set S ⊆ <n is convex if 8x; y 2 S, λx + (1 − λ)y 2 S, 8λ 2 [0; 1]. Figure 1: Examples of convex and non convex sets Given a set of inequalities we define the feasible region as P = fx 2 <n : Ax ≤ bg. We say that P is a polyhedron. Which points on this figure can have the optimal value? Our intuition from last time is that Figure 2: Example of a polyhedron. \Circled" corners are feasible and \squared" are non feasible optimal solutions to linear programming problems occur at \corners" of the feasible region. What we'd like to do now is to consider formal definitions of the \corners" of the feasible region. 3-1 One idea is that a point in the polyhedron is a corner if there is some objective function that is minimized there uniquely. Definition 2 x 2 P is a vertex of P if 9c 2 <n with cT x < cT y; 8y 6= x; y 2 P . Another idea is that a point x 2 P is a corner if there are no small perturbations of x that are in P . Definition 3 Let P be a convex set in <n. Then x 2 P is an extreme point of P if x cannot be written as λy + (1 − λ)z for y; z 2 P , y; z 6= x, 0 ≤ λ ≤ 1.
[Show full text]
Archimedean Solids
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 Archimedean Solids Anna Anderson University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Anderson, Anna, "Archimedean Solids" (2008). MAT Exam Expository Papers. 4. https://digitalcommons.unl.edu/mathmidexppap/4 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Archimedean Solids Anna Anderson In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor July 2008 2 Archimedean Solids A polygon is a simple, closed, planar figure with sides formed by joining line segments, where each line segment intersects exactly two others. If all of the sides have the same length and all of the angles are congruent, the polygon is called regular. The sum of the angles of a regular polygon with n sides, where n is 3 or more, is 180° x (n – 2) degrees. If a regular polygon were connected with other regular polygons in three dimensional space, a polyhedron could be created. In geometry, a polyhedron is a three- dimensional solid which consists of a collection of polygons joined at their edges. The word polyhedron is derived from the Greek word poly (many) and the Indo-European term hedron (seat).
[Show full text]
Circle Theorems
Circle theorems A LEVEL LINKS Scheme of work: 2b. Circles – equation of a circle, geometric problems on a grid Key points • A chord is a straight line joining two points on the circumference of a circle. So AB is a chord. • A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90°. • Two tangents on a circle that meet at a point outside the circle are equal in length. So AC = BC. • The angle in a semicircle is a right angle. So angle ABC = 90°. • When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference. So angle AOB = 2 × angle ACB. • Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal. So angle ACB = angle ADB and angle CAD = angle CBD. • A cyclic quadrilateral is a quadrilateral with all four vertices on the circumference of a circle. Opposite angles in a cyclic quadrilateral total 180°. So x + y = 180° and p + q = 180°. • The angle between a tangent and chord is equal to the angle in the alternate segment, this is known as the alternate segment theorem. So angle BAT = angle ACB. Examples Example 1 Work out the size of each angle marked with a letter. Give reasons for your answers. Angle a = 360° − 92° 1 The angles in a full turn total 360°. = 268° as the angles in a full turn total 360°.
[Show full text]
Descriptive Geometry Section 10.1 Basic Descriptive Geometry and Board Drafting Section 10.2 Solving Descriptive Geometry Problems with CAD
10 Descriptive Geometry Section 10.1 Basic Descriptive Geometry and Board Drafting Section 10.2 Solving Descriptive Geometry Problems with CAD Chapter Objectives • Locate points in three-dimensional (3D) space. • Identify and describe the three basic types of lines. • Identify and describe the three basic types of planes. • Solve descriptive geometry problems using board-drafting techniques. • Create points, lines, planes, and solids in 3D space using CAD. • Solve descriptive geometry problems using CAD. Plane Spoken Rutan’s unconventional 202 Boomerang aircraft has an asymmetrical design, with one engine on the fuselage and another mounted on a pod. What special allowances would need to be made for such a design? 328 Drafting Career Burt Rutan, Aeronautical Engineer Efﬁ cient travel through space has become an ambi- tion of aeronautical engineer, Burt Rutan. “I want to go high,” he says, “because that’s where the view is.” His unconventional designs have included every- thing from crafts that can enter space twice within a two week period, to planes than can circle the Earth without stopping to refuel. Designed by Rutan and built at his company, Scaled Composites LLC, the 202 Boomerang aircraft is named for its forward-swept asymmetrical wing. The design allows the Boomerang to ﬂ y faster and farther than conventional twin-engine aircraft, hav- ing corrected aerodynamic mistakes made previously in twin-engine design. It is hailed as one of the most beautiful aircraft ever built. Academic Skills and Abilities • Algebra, geometry, calculus • Biology, chemistry, physics • English • Social studies • Humanities • Computer use Career Pathways Engineers should be creative, inquisitive, ana- lytical, detail oriented, and able to work as part of a team and to communicate well.
[Show full text]
1-1 Understanding Points, Lines, and Planes Lines, and Planes
Understanding Points, 1-11-1 Understanding Points, Lines, and Planes Lines, and Planes Holt Geometry 1-1 Understanding Points, Lines, and Planes Objectives Identify, name, and draw points, lines, segments, rays, and planes. Apply basic facts about points, lines, and planes. Holt Geometry 1-1 Understanding Points, Lines, and Planes Vocabulary undefined term point line plane collinear coplanar segment endpoint ray opposite rays postulate Holt Geometry 1-1 Understanding Points, Lines, and Planes The most basic figures in geometry are undefined terms, which cannot be defined by using other figures. The undefined terms point, line, and plane are the building blocks of geometry. Holt Geometry 1-1 Understanding Points, Lines, and Planes Holt Geometry 1-1 Understanding Points, Lines, and Planes Points that lie on the same line are collinear. K, L, and M are collinear. K, L, and N are noncollinear. Points that lie on the same plane are coplanar. Otherwise they are noncoplanar. K L M N Holt Geometry 1-1 Understanding Points, Lines, and Planes Example 1: Naming Points, Lines, and Planes A. Name four coplanar points. A, B, C, D B. Name three lines. Possible answer: AE, BE, CE Holt Geometry 1-1 Understanding Points, Lines, and Planes Holt Geometry 1-1 Understanding Points, Lines, and Planes Example 2: Drawing Segments and Rays Draw and label each of the following. A. a segment with endpoints M and N. N M B. opposite rays with a common endpoint T. T Holt Geometry 1-1 Understanding Points, Lines, and Planes Check It Out! Example 2 Draw and label a ray with endpoint M that contains N.
[Show full text]
Digital Geometry Processing Mesh Basics
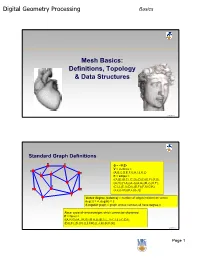
Digital Geometry Processing Basics Mesh Basics: Definitions, Topology & Data Structures 1 © Alla Sheffer Standard Graph Definitions G = <V,E> V = vertices = {A,B,C,D,E,F,G,H,I,J,K,L} E = edges = {(A,B),(B,C),(C,D),(D,E),(E,F),(F,G), (G,H),(H,A),(A,J),(A,G),(B,J),(K,F), (C,L),(C,I),(D,I),(D,F),(F,I),(G,K), (J,L),(J,K),(K,L),(L,I)} Vertex degree (valence) = number of edges incident on vertex deg(J) = 4, deg(H) = 2 k-regular graph = graph whose vertices all have degree k Face: cycle of vertices/edges which cannot be shortened F = faces = {(A,H,G),(A,J,K,G),(B,A,J),(B,C,L,J),(C,I,L),(C,D,I), (D,E,F),(D,I,F),(L,I,F,K),(L,J,K),(K,F,G)} © Alla Sheffer Page 1 Digital Geometry Processing Basics Connectivity Graph is connected if there is a path of edges connecting every two vertices Graph is k-connected if between every two vertices there are k edge-disjoint paths Graph G’=<V’,E’> is a subgraph of graph G=<V,E> if V’ is a subset of V and E’ is the subset of E incident on V’ Connected component of a graph: maximal connected subgraph Subset V’ of V is an independent set in G if the subgraph it induces does not contain any edges of E © Alla Sheffer Graph Embedding Graph is embedded in Rd if each vertex is assigned a position in Rd Embedding in R2 Embedding in R3 © Alla Sheffer Page 2 Digital Geometry Processing Basics Planar Graphs Planar Graph Plane Graph Planar graph: graph whose vertices and edges can Straight Line Plane Graph be embedded in R2 such that its edges do not intersect Every planar graph can be drawn as a straight-line plane graph ©
[Show full text]
Machine Drawing
2.4 LINES Lines of different types and thicknesses are used for graphical representation of objects. The types of lines and their applications are shown in Table 2.4. Typical applications of different types of lines are shown in Figs. 2.5 and 2.6. Table 2.4 Types of lines and their applications Line Description General Applications A Continuous thick A1 Visible outlines B Continuous thin B1 Imaginary lines of intersection (straight or curved) B2 Dimension lines B3 Projection lines B4 Leader lines B5 Hatching lines B6 Outlines of revolved sections in place B7 Short centre lines C Continuous thin, free-hand C1 Limits of partial or interrupted views and sections, if the limit is not a chain thin D Continuous thin (straight) D1 Line (see Fig. 2.5) with zigzags E Dashed thick E1 Hidden outlines G Chain thin G1 Centre lines G2 Lines of symmetry G3 Trajectories H Chain thin, thick at ends H1 Cutting planes and changes of direction J Chain thick J1 Indication of lines or surfaces to which a special requirement applies K Chain thin, double-dashed K1 Outlines of adjacent parts K2 Alternative and extreme positions of movable parts K3 Centroidal lines 2.4.2 Order of Priority of Coinciding Lines When two or more lines of different types coincide, the following order of priority should be observed: (i) Visible outlines and edges (Continuous thick lines, type A), (ii) Hidden outlines and edges (Dashed line, type E or F), (iii) Cutting planes (Chain thin, thick at ends and changes of cutting planes, type H), (iv) Centre lines and lines of symmetry (Chain thin line, type G), (v) Centroidal lines (Chain thin double dashed line, type K), (vi) Projection lines (Continuous thin line, type B).
[Show full text]
Measure, Integral and Probability
Marek Capinski´ and Ekkehard Kopp Measure, Integral and Probability Springer-Verlag Berlin Heidelberg NewYork London Paris Tokyo Hong Kong Barcelona Budapest To our children; grandchildren: Piotr, Maciej, Jan, Anna; Luk asz Anna, Emily Preface The central concepts in this book are Lebesgue measure and the Lebesgue integral. Their role as standard fare in UK undergraduate mathematics courses is not wholly secure; yet they provide the principal model for the development of the abstract measure spaces which underpin modern probability theory, while the Lebesgue function spaces remain the main source of examples on which to test the methods of functional analysis and its many applications, such as Fourier analysis and the theory of partial differential equations. It follows that not only budding analysts have need of a clear understanding of the construction and properties of measures and integrals, but also that those who wish to contribute seriously to the applications of analytical methods in a wide variety of areas of mathematics, physics, electronics, engineering and, most recently, finance, need to study the underlying theory with some care. We have found remarkably few texts in the current literature which aim explicitly to provide for these needs, at a level accessible to current under- graduates. There are many good books on modern probability theory, and increasingly they recognize the need for a strong grounding in the tools we develop in this book, but all too often the treatment is either too advanced for an undergraduate audience or else somewhat perfunctory. We hope therefore that the current text will not be regarded as one which fills a much-needed gap in the literature! One fundamental decision in developing a treatment of integration is whether to begin with measures or integrals, i.e.
[Show full text]
Angles ANGLE Topics • Coterminal Angles • Defintion of an Angle
Angles ANGLE Topics • Coterminal Angles • Defintion of an angle • Decimal degrees to degrees, minutes, seconds by hand using the TI-82 or TI-83 Plus • Degrees, seconds, minutes changed to decimal degree by hand using the TI-82 or TI-83 Plus • Standard position of an angle • Positive and Negative angles ___________________________________________________________________________ Definition: Angle An angle is created when a half-ray (the initial side of the angle) is drawn out of a single point (the vertex of the angle) and the ray is rotated around the point to another location (becoming the terminal side of the angle). An angle is created when a half-ray (initial side of angle) A: vertex point of angle is drawn out of a single point (vertex) AB: Initial side of angle. and the ray is rotated around the point to AC: Terminal side of angle another location (becoming the terminal side of the angle). Hence angle A is created (also called angle BAC) STANDARD POSITION An angle is in "standard position" when the vertex is at the origin and the initial side of the angle is along the positive x-axis. Recall: polynomials in algebra have a standard form (all the terms have to be listed with the term having the highest exponent first). In trigonometry, there is a standard position for angles. In this way, we are all talking about the same thing and are not trying to guess if your math solution and my math solution are the same. Not standard position. Not standard position. This IS standard position. Initial side not along Initial side along negative Initial side IS along the positive x-axis.
[Show full text]
The Axiom of Choice and Its Implications
THE AXIOM OF CHOICE AND ITS IMPLICATIONS KEVIN BARNUM Abstract. In this paper we will look at the Axiom of Choice and some of the various implications it has. These implications include a number of equivalent statements, and also some less accepted ideas. The proofs discussed will give us an idea of why the Axiom of Choice is so powerful, but also so controversial. Contents 1. Introduction 1 2. The Axiom of Choice and Its Equivalents 1 2.1. The Axiom of Choice and its Well-known Equivalents 1 2.2. Some Other Less Well-known Equivalents of the Axiom of Choice 3 3. Applications of the Axiom of Choice 5 3.1. Equivalence Between The Axiom of Choice and the Claim that Every Vector Space has a Basis 5 3.2. Some More Applications of the Axiom of Choice 6 4. Controversial Results 10 Acknowledgments 11 References 11 1. Introduction The Axiom of Choice states that for any family of nonempty disjoint sets, there exists a set that consists of exactly one element from each element of the family. It seems strange at ﬁrst that such an innocuous sounding idea can be so powerful and controversial, but it certainly is both. To understand why, we will start by looking at some statements that are equivalent to the axiom of choice. Many of these equivalences are very useful, and we devote much time to one, namely, that every vector space has a basis. We go on from there to see a few more applications of the Axiom of Choice and its equivalents, and ﬁnish by looking at some of the reasons why the Axiom of Choice is so controversial.
[Show full text]
A Historical Introduction to Elementary Geometry
i MATH 119 – Fall 2012: A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning “earth measure” ( ge = earth or land ) + ( metria = measure ) . Euclid wrote the Elements of geometry between 330 and 320 B.C. It was a compilation of the major theorems on plane and solid geometry presented in an axiomatic style. Near the beginning of the first of the thirteen books of the Elements, Euclid enumerated five fundamental assumptions called postulates or axioms which he used to prove many related propositions or theorems on the geometry of two and three dimensions. POSTULATE 1. Any two points can be joined by a straight line. POSTULATE 2. Any straight line segment can be extended indefinitely in a straight line. POSTULATE 3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center. POSTULATE 4. All right angles are congruent. POSTULATE 5. (Parallel postulate) If two lines intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. The circle described in postulate 3 is tacitly unique. Postulates 3 and 5 hold only for plane geometry; in three dimensions, postulate 3 defines a sphere. Postulate 5 leads to the same geometry as the following statement, known as Playfair's axiom, which also holds only in the plane: Through a point not on a given straight line, one and only one line can be drawn that never meets the given line.
[Show full text]
Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
[Show full text]