Feature Selection and Dimension Reduction
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Game 7S Apr 22 1.Pdf
FOR IMMEDIATE RELEASE APRIL 22, 2019 STANLEY CUP PLAYOFF SECOND-ROUND BERTHS AT STAKE IN GAME 7 DOUBLEHEADER TUESDAY NEW YORK (April 22, 2019) -- Two Stanley Cup Playoff series will be decided in a Game 7 doubleheader Tuesday when the Boston Bruins play host to the Toronto Maple Leafs (7 p.m., ET, NBCSN, Sportsnet, CBC, TVAS), followed by the San Jose Sharks facing the Vegas Golden Knights (10 p.m., ET, NBCSN, Sportsnet, TVAS). The past two playoff series between the Bruins and Maple Leafs have culminated in unprecedented Game 7 drama, both occurring at TD Garden. In 2013, Boston became the first team in NHL history to overcome a three-goal, third-period deficit to win a Game 7 (Boston 5, Toronto 4 ,OT). In 2018, the Bruins became the first team in League history to overcome three deficits of at least one goal to win a Game 7 in regulation (Boston 7, Toronto 4). Five current Bruins appeared in both the 2013 and 2018 contests: goaltender Tuukka Rask, defenseman Zdeno Chara and forwards Patrice Bergeron, Brad Marchand and David Krejci. Two Maple Leafs players have done so: defenseman Jake Gardiner and forward Nazem Kadri. Chara (0-4--4 in 12 GP) is set to tie an NHL record by playing in his 13th career Game 7, joining all-time co-leaders Patrick Roy and Scott Stevens. Most Game 7 Appearances, All Time Most Game 7 Appearances, Active Patrick Roy 13 Zdeno Chara, BOS 12 Scott Stevens 13 Nicklas Backstrom, WSH 11 Zdeno Chara 12 Alex Ovechkin, WSH 11 Glenn Anderson 12 Patrice Bergeron, BOS 10 Ken Daneyko 12 Chris Kunitz, CHI 10 Stephane Yelle 12 Milan Lucic, EDM 10 Dave Andreychuk 11 David Krejci, BOS 9 Nicklas Backstrom 11 Valtteri Filppula, NYI 9 Doug Gilmour 11 Dan Girardi, TBL 9 Al MacInnis 11 Mike Green, DET 9 Alex Ovechkin 11 Carl Hagelin, WSH 9 Mark Recchi 11 Anton Stralman, TBL 9 The Sharks (6-4 in Game 7s) will host a series-decider for the fifth time, having won three of their previous four contests on home ice. -

Boston Bruins Playoff Game Notes
Boston Bruins Playoff Game Notes Sat, Apr 13, 2019 Round 1 Game 2 Boston Bruins 0 - 1 Toronto Maple Leafs 1 - 0 Team Game: 2 0 - 1 (Home) Team Game: 2 0 - 0 (Home) Home Game: 2 0 - 0 (Road) Road Game: 2 1 - 0 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 31 Zane McIntyre - - - - - - 30 Michael Hutchinson - - - - - - 40 Tuukka Rask 1 0 1 0 3.05 .906 31 Frederik Andersen 1 1 0 0 1.00 .974 41 Jaroslav Halak - - - - - - 35 Joseph Woll - - - - - - 40 Garret Sparks - - - - - - # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 13 C Charlie Coyle 1 0 0 0 -1 0 2 D Ron Hainsey 1 0 0 0 2 0 14 R Chris Wagner 1 0 0 0 0 0 3 D Justin Holl - - - - - - 20 C Joakim Nordstrom 1 0 0 0 0 0 8 D Jake Muzzin 1 0 1 1 1 0 25 D Brandon Carlo 1 0 0 0 0 0 11 L Zach Hyman 1 0 0 0 2 0 27 D John Moore - - - - - - 12 C Patrick Marleau 1 0 1 1 1 0 33 D Zdeno Chara 1 0 0 0 -1 2 16 R Mitchell Marner 1 2 0 2 3 0 37 C Patrice Bergeron 1 1 0 1 -2 0 18 L Andreas Johnsson 1 0 0 0 0 0 42 R David Backes - - - - - - 19 C Nic Petan - - - - - - 43 C Danton Heinen 1 0 0 0 -1 0 22 D Nikita Zaitsev 1 0 0 0 2 0 44 D Steven Kampfer - - - - - - 23 D Travis Dermott 1 0 0 0 0 0 46 C David Krejci 1 0 0 0 -1 0 24 R Kasperi Kapanen 1 0 0 0 0 2 47 D Torey Krug 1 0 1 1 -1 0 28 R Connor Brown 1 0 0 0 0 0 48 D Matt Grzelcyk 1 0 0 0 -1 0 29 R William Nylander 1 1 0 1 1 2 52 C Sean Kuraly - - - - - - 33 C Frederik Gauthier 1 0 0 0 0 0 55 C Noel Acciari 1 0 0 0 0 0 34 C Auston Matthews 1 0 0 0 0 0 63 L Brad Marchand 1 0 1 1 -2 0 42 L Trevor Moore 1 0 0 0 0 0 73 D Charlie McAvoy -

Turnbull Hockey Pool For
Turnbull Hockey Pool for Each year, Turnbull students participate in several fundraising initiatives, which we promote as a way to develop a sense of community, leadership and social responsibility within the students. Last year's grade 7 and 8 students put forth a great deal of effort campaigning friends and family members to join Turnbull's annual NHL hockey pool, raising a total of $1750 for a charity of their choice (the United Way). This year's group has decided to run the hockey pool for the benefit of Help Lesotho, an international development organization working in the AIDS-ravaged country of Lesotho in southern Africa. From www.helplesotho.org "Help Lesotho’s programs foster hope and motivation in those who are most in need: orphans, vulnerable children, at-risk youth and grandmothers. Our work targets root causes and community priorities, including literacy, youth leadership training, school twinning, child sponsorship and gender programming. Help Lesotho is an effective, sustainable organization that is working at the grass-roots level to support the next generation of leaders in Lesotho." Your participation in this year's NHL hockey pool is very much appreciated. We believe it will provide students and their friends and families an opportunity to have fun together while giving back to their community by raising awareness and funds for a great cause. Prizes: > Grand Prize awarded to contestant whose team accumulates the most points over the regular NHL season = 10" Samsung Galaxy Tablet > Monthly Prizes awarded to the contestants whose teams accumulate the most points over each designated period (see website) = Two Movie Passes How it Works: > Everyone in the community is welcome to join in on the fun. -

NHL Playoffs PDF.Xlsx
Anaheim Ducks Boston Bruins POS PLAYER GP G A PTS +/- PIM POS PLAYER GP G A PTS +/- PIM F Ryan Getzlaf 74 15 58 73 7 49 F Brad Marchand 80 39 46 85 18 81 F Ryan Kesler 82 22 36 58 8 83 F David Pastrnak 75 34 36 70 11 34 F Corey Perry 82 19 34 53 2 76 F David Krejci 82 23 31 54 -12 26 F Rickard Rakell 71 33 18 51 10 12 F Patrice Bergeron 79 21 32 53 12 24 F Patrick Eaves~ 79 32 19 51 -2 24 D Torey Krug 81 8 43 51 -10 37 F Jakob Silfverberg 79 23 26 49 10 20 F Ryan Spooner 78 11 28 39 -8 14 D Cam Fowler 80 11 28 39 7 20 F David Backes 74 17 21 38 2 69 F Andrew Cogliano 82 16 19 35 11 26 D Zdeno Chara 75 10 19 29 18 59 F Antoine Vermette 72 9 19 28 -7 42 F Dominic Moore 82 11 14 25 2 44 F Nick Ritchie 77 14 14 28 4 62 F Drew Stafford~ 58 8 13 21 6 24 D Sami Vatanen 71 3 21 24 3 30 F Frank Vatrano 44 10 8 18 -3 14 D Hampus Lindholm 66 6 14 20 13 36 F Riley Nash 81 7 10 17 -1 14 D Josh Manson 82 5 12 17 14 82 D Brandon Carlo 82 6 10 16 9 59 F Ondrej Kase 53 5 10 15 -1 18 F Tim Schaller 59 7 7 14 -6 23 D Kevin Bieksa 81 3 11 14 0 63 F Austin Czarnik 49 5 8 13 -10 12 F Logan Shaw 55 3 7 10 3 10 D Kevan Miller 58 3 10 13 1 50 D Shea Theodore 34 2 7 9 -6 28 D Colin Miller 61 6 7 13 0 55 D Korbinian Holzer 32 2 5 7 0 23 D Adam McQuaid 77 2 8 10 4 71 F Chris Wagner 43 6 1 7 2 6 F Matt Beleskey 49 3 5 8 -10 47 D Brandon Montour 27 2 4 6 11 14 F Noel Acciari 29 2 3 5 3 16 D Clayton Stoner 14 1 2 3 0 28 D John-Michael Liles 36 0 5 5 1 4 F Ryan Garbutt 27 2 1 3 -3 20 F Jimmy Hayes 58 2 3 5 -3 29 F Jared Boll 51 0 3 3 -3 87 F Peter Cehlarik 11 0 2 2 -

1 Columbus Blue Jackets News Clips November 8, 2017 Columbus Blue
Columbus Blue Jackets News Clips November 8, 2017 Columbus Blue Jackets PAGE 02: Columbus Dispatch: Blue Jackets: Panarin says he was pressing, glad to get second goal PAGE 04: Columbus Dispatch: Blue Jackets: Atkinson activated, expected to play against Nashville PAGE 05: Columbus Dispatch: Predators 3 / Blue Jackets 1 | Jackets’ offense weak around the net in loss PAGE 07: Columbus Dispatch: Blue Jackets’ Cam Atkinson glad to be back after injury, illness PAGE 08: Columbus Dispatch: Deal for Duchene just too pricey for Jackets PAGE 10: The Athletic: Cam Atkinson returns tonight, plus Scott Hartnell's first game back and more PAGE 12: The Athletic: Slowly and surely, Blue Jackets rookie Pierre-Luc Dubois is coming of age Cleveland Monsters/Prospects NHL/Websites PAGE 15: The Athletic: LeBrun Notebook: Joe Sakic believes Samuel Girard key to Avs rebuild, Blue Jackets seeking centre PAGE 17: Sportsnet.ca: 31 Thoughts: Inside the Matt Duchene-Kyle Turris blockbuster PAGE 26: Sportsnet.ca: Wojtek Wolski aims for Team Canada Olympic spot after career- threatening injury PAGE 28: USA Today: After blockbuster, here are six players who could be traded this season 1 http://www.dispatch.com/sports/20171107/blue-jackets-panarin-says-he-was-pressing-glad-to-get- second-goal Blue Jackets: Panarin says he was pressing, glad to get second goal By Steve Gorten – November 7, 2017 NEW YORK — Blue Jackets winger Artemi Panarin ended his 10-game goal drought Monday night and joked after the game that it wasn’t a coincidence both of his goals this season have come against the Rangers. -

BOSTON BRUINS Vs. OTTAWA SENATORS
BOSTON BRUINS vs. OTTAWA SENATORS POST GAME NOTES MILESTONES REACHED: • Patrice Bergeron recorded his 500th NHL assist tonight ... He is the 15th active player to reach that milestone. WHO’S HOT: • David Pastrnak had a goal and two assists tonight, extending his point streak to 11 games with 13-14=27 totals in that span. • Patrice Bergeron had a goal and an assist tonight, giving him 6-8=14 totals in ten of his last 12 games. • Brad Marchand had a goal and an assist tonight, extending his assist streak to 11 games and his point streak to 12 games with 8-15=23 totals in that stretch ... Both are career-best streaks. • Danton Heinen had a goal and an assist tonight, giving him 2-3=5 totals in four of his last six games. • Jake DeBrusk had a goal tonight, giving him 2-2=4 totals in four of his last four of his last six games. • Torey Krug had an assist tonight, giving him eight assists in six of his last eight games. • Ottawa’s Mark Borowiecki had two assists tonight, giving him 1-3=4 totals in three of his last four games. • Ottawa’s Anthony Duclair had a goal tonight, giving him 4-1=5 totals in four straight games. • Ottawa’s Connor Brown had a goal tonight, extending his point streak to five games with 2-4=6 totals in that stretch. • Ottawa’s Logan Brown had an assist tonight for his second assist in his last three games. • Ottawa’s Dylan DeMelo had an assist tonight, giving him three assists in his last two straight games. -

Wisconsin 0 0 0 Vs. Victoria 0
6 NCAA Championships ▪ 16 Conference Championships ▪ 39 All-Americans ▪ 23 Olympians ▪ 80 Badgers in the NHL 201617 SCHEDULE/RESULTS WISCONSIN 000 VS. VICTORIA 000 0-0-0, 0-0-0-0 Big Ten OCT. 1, 2016 ▪ 7 P.M. &CT* ▪ MADISON, WIS ▪ KOHL CENTER &15,359* Date Opponent Time/Result WISCONSIN BADGERS VICTORIA VIKES OCT. 1 VICTORIA (EXH) 7 P.M. Head Coach: Tony Granato Head Coach: Harry Schamhart Oct. 7 vs. Northern Michigan^ 7 p.m. Record at WIS: 0-0-0 (1st Year) Record at Victoria: (12th Year) Oct. 8 vs. Northern Michigan^ 7 p.m. Overall: 0-0-0 (1st Year) Overall: (12th Year) OCT. 14 BOSTON COLLEGE 7 P.M. EXHIBITION OCT. 15 BOSTON COLLEGE 3 P.M. OCT. 21 U.S. UNDER-18 TEAM (EXH) 7 P.M. Oct. 28 at St. Lawrence 6 p.m. NEW ERA BEGINS Oct. 29 at Clarkson 6:30 p.m. n Wisconsin begins a new era with its first-year coaching NOV. 4 NORTHERN MICHIGAN 7 P.M. staff of head coach Tony Granato, and associate head NOV. 5 NORTHERN MICHIGAN 7 P.M. coaches Don Granato and Mark Osiecki. NOV. 18 MERRIMACK 7 P.M. NOV. 19 MERRIMACK 7 P.M. n Tony Granato returns to Wisconsin a er 13 years as a Nov. 25 at Colorado College 8:30 p.m. head and assistant coach in the NHL with the Detroit Nov. 26 at Denver 8 p.m. Red Wings, Pi sburgh Penguins and Colorado Avalanche. DEC. 2 OMAHA 7:30 P.M. That followed a 13-year NHL playing career that included DEC. -
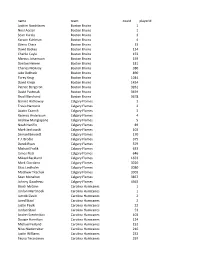
2019 Playoff Draft Player Frequency Report
name team count playerid Joakim Nordstrom Boston Bruins 1 Noel Acciari Boston Bruins 1 Sean Kuraly Boston Bruins 3 Karson Kuhlman Boston Bruins 4 Zdeno Chara Boston Bruins 13 David Backes Boston Bruins 134 Charlie Coyle Boston Bruins 153 Marcus Johansson Boston Bruins 159 Danton Heinen Boston Bruins 181 Charles McAvoy Boston Bruins 380 Jake DeBrusk Boston Bruins 890 Torey Krug Boston Bruins 1044 David Krejci Boston Bruins 1434 Patrice Bergeron Boston Bruins 3261 David Pastrnak Boston Bruins 3459 Brad Marchand Boston Bruins 3678 Garnet Hathaway Calgary Flames 2 Travis Hamonic Calgary Flames 2 Austin Czarnik Calgary Flames 3 Rasmus Andersson Calgary Flames 4 Andrew Mangiapane Calgary Flames 5 Noah Hanifin Calgary Flames 89 Mark Jankowski Calgary Flames 102 Samuel Bennett Calgary Flames 170 T.J. Brodie Calgary Flames 375 Derek Ryan Calgary Flames 379 Michael Frolik Calgary Flames 633 James Neal Calgary Flames 646 Mikael Backlund Calgary Flames 1653 Mark Giordano Calgary Flames 3020 Elias Lindholm Calgary Flames 3080 Matthew Tkachuk Calgary Flames 3303 Sean Monahan Calgary Flames 3857 Johnny Gaudreau Calgary Flames 4363 Brock McGinn Carolina Hurricanes 1 Jordan Martinook Carolina Hurricanes 1 Jaccob Slavin Carolina Hurricanes 2 Jared Staal Carolina Hurricanes 2 Justin Faulk Carolina Hurricanes 22 Jordan Staal Carolina Hurricanes 53 Andrei Svechnikov Carolina Hurricanes 103 Dougie Hamilton Carolina Hurricanes 124 Michael Ferland Carolina Hurricanes 152 Nino Niederreiter Carolina Hurricanes 216 Justin Williams Carolina Hurricanes 232 Teuvo Teravainen Carolina Hurricanes 297 Sebastian Aho Carolina Hurricanes 419 Nikita Zadorov Colorado Avalanche 1 Samuel Girard Colorado Avalanche 1 Matthew Nieto Colorado Avalanche 1 Cale Makar Colorado Avalanche 2 Erik Johnson Colorado Avalanche 2 Tyson Jost Colorado Avalanche 3 Josh Anderson Colorado Avalanche 14 Colin Wilson Colorado Avalanche 14 Matt Calvert Colorado Avalanche 14 Derick Brassard Colorado Avalanche 28 J.T. -

Sport-Scan Daily Brief
SPORT-SCAN DAILY BRIEF NHL 04/14/18 Anaheim Ducks Columbus Blue Jackets 1091262 Ducks hope momentum swings their way in Game 2 1091297 Blue Jackets | Nick Foligno’s ‘save,’ return from injury set against Sharks tone 1091263 Alexander: Ducks are forced back into response mode 1091298 One win means little in series, but plenty to Jackets fans 1091264 Ducks take clean slate approach after making a mess of 1091299 Blue Jackets | Injury report: Alexander Wennberg Game 1 against Sharks ‘doubtful’; Capitals defenseman may be out 1091265 Ducks must generate more shots, limit Sharks’ Brent 1091300 Blue Jackets | Gritty group guts out yet another close win Burns in Game 2 1091301 Blue Jackets | Alexander Wennberg doubtful for Game 2, Jarmo Kekalainen says Boston Bruins 1091302 Can strong finish to regular season carry over? It did for 1091266 Maple Leafs’ Nazem Kadri suspended for three games one night with Blue Jackets 1091267 That end-of-season Bruins slump was nothing to worry 1091303 Projecting Team USA's roster for the World about Championships 1091268 Brad Marchand finds a new way to get in his licks 1091269 Riley Nash’s status for Game 2 is still uncertain Dallas Stars 1091270 Why did Brad Marchand lick Leo Komarov in Game 1? 1091304 Vote! Who you want Stars to hire as next coach? 1091271 The Bruins came to play, and the Maple Leafs crumbled 1091305 Here's why the next Stars head coach will reap rewards 1091272 Evander Kane scores his first two career playoff goals in from Ken Hitchcock's groundwork Sharks’ win over Ducks 1091306 Player grades: Vote on Stars workhorse Radek Faksa's 1091273 Devils can’t complete comeback vs. -
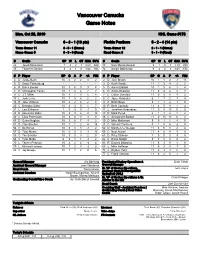
Vancouver Canucks Game Notes
Vancouver Canucks Game Notes Mon, Oct 28, 2019 NHL Game #178 Vancouver Canucks 6 - 3 - 1 (13 pts) Florida Panthers 5 - 2 - 4 (14 pts) Team Game: 11 3 - 0 - 1 (Home) Team Game: 12 2 - 1 - 1 (Home) Home Game: 5 3 - 3 - 0 (Road) Road Game: 8 3 - 1 - 3 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 25 Jacob Markstrom 7 4 2 1 2.53 .920 33 Sam Montembeault 3 1 0 1 1.79 .933 35 Thatcher Demko 3 2 1 0 1.64 .943 72 Sergei Bobrovsky 9 4 2 3 3.65 .874 # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 4 D Jordie Benn 10 0 2 2 4 2 2 D Josh Brown 10 1 1 2 -1 11 5 D Oscar Fantenberg - - - - - - 3 D Keith Yandle 11 1 3 4 2 2 6 R Brock Boeser 10 3 6 9 3 4 5 D Aaron Ekblad 10 1 5 6 1 4 8 D Christopher Tanev 10 1 3 4 2 2 6 D Anton Stralman 11 0 4 4 3 2 9 C J.T. Miller 10 4 7 11 5 8 7 C Colton Sceviour 11 0 3 3 -1 2 17 L Josh Leivo 10 1 3 4 2 2 8 C Jayce Hawryluk 6 1 1 2 -1 4 18 R Jake Virtanen 10 2 2 4 2 4 9 C Brian Boyle 3 1 1 2 1 0 20 C Brandon Sutter 10 2 3 5 1 7 10 R Brett Connolly 11 4 5 9 1 4 21 L Loui Eriksson 1 0 0 0 -1 0 11 L Jonathan Huberdeau 11 5 8 13 0 8 23 D Alexander Edler 10 3 3 6 0 10 13 D Mark Pysyk 6 1 1 2 1 2 40 C Elias Pettersson 10 3 8 11 3 0 16 C Aleksander Barkov 11 0 13 13 0 2 43 D Quinn Hughes 10 1 6 7 -1 2 19 D Mike Matheson 9 0 1 1 -1 0 51 D Troy Stecher 10 1 1 2 4 16 21 C Vincent Trocheck 8 1 5 6 -2 0 53 C Bo Horvat 10 5 3 8 -1 2 52 D MacKenzie Weegar 11 3 5 8 2 4 57 D Tyler Myers 10 0 3 3 -1 10 55 C Noel Acciari 11 4 0 4 -1 0 59 C Tim Schaller 10 3 0 3 2 8 61 D Riley Stillman 1 0 0 0 -3 5 64 C Tyler Motte 6 0 1 1 -1 2 62 C Denis Malgin 9 3 5 8 4 2 70 L Tanner Pearson 10 2 2 4 -4 4 63 R Evgenii Dadonov 11 6 3 9 1 0 79 L Micheal Ferland 10 1 2 3 -2 2 68 L Mike Hoffman 11 5 3 8 -1 6 83 C Jay Beagle 10 1 1 2 0 6 73 L Dryden Hunt 11 0 3 3 2 8 77 C Frank Vatrano 11 3 2 5 1 4 General Manager Jim Benning President of Hockey Operations & Dale Tallon Assistant General Manager John Weisbrod General Manager Head Coach Travis Green Sr. -
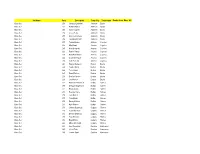
Set Name Card Description Team City Team Name Rookie Auto
Set Name Card Description Team City Team Name Rookie Auto Mem #'d Base Set 251 Hampus Lindholm Anaheim Ducks Base Set 252 Rickard Rakell Anaheim Ducks Base Set 253 Sami Vatanen Anaheim Ducks Base Set 254 Corey Perry Anaheim Ducks Base Set 255 Antoine Vermette Anaheim Ducks Base Set 256 Jonathan Bernier Anaheim Ducks Base Set 257 Tobias Rieder Arizona Coyotes Base Set 258 Max Domi Arizona Coyotes Base Set 259 Alex Goligoski Arizona Coyotes Base Set 260 Radim Vrbata Arizona Coyotes Base Set 261 Brad Richardson Arizona Coyotes Base Set 262 Louis Domingue Arizona Coyotes Base Set 263 Luke Schenn Arizona Coyotes Base Set 264 Patrice Bergeron Boston Bruins Base Set 265 Tuukka Rask Boston Bruins Base Set 266 Torey Krug Boston Bruins Base Set 267 David Backes Boston Bruins Base Set 268 Dominic Moore Boston Bruins Base Set 269 Joe Morrow Boston Bruins Base Set 270 Rasmus Ristolainen Buffalo Sabres Base Set 271 Zemgus Girgensons Buffalo Sabres Base Set 272 Brian Gionta Buffalo Sabres Base Set 273 Evander Kane Buffalo Sabres Base Set 274 Jack Eichel Buffalo Sabres Base Set 275 Tyler Ennis Buffalo Sabres Base Set 276 Dmitry Kulikov Buffalo Sabres Base Set 277 Kyle Okposo Buffalo Sabres Base Set 278 Johnny Gaudreau Calgary Flames Base Set 279 Sean Monahan Calgary Flames Base Set 280 Dennis Wideman Calgary Flames Base Set 281 Troy Brouwer Calgary Flames Base Set 282 Brian Elliott Calgary Flames Base Set 283 Micheal Ferland Calgary Flames Base Set 284 Lee Stempniak Carolina Hurricanes Base Set 285 Victor Rask Carolina Hurricanes Base Set 286 Jordan -

Hockey Trivia Questions
Hockey Trivia Questions 1. Q: What hockey team has won the most Stanley cups? A: Montreal Canadians 2. Who scored a record 10 hat tricks in one NHL season? A: Wayne Gretzky 3. Q: What hockey speedster is nicknamed the Russian Rocket? A: Pavel Bure 4. Q: What is the penalty for fighting in the NHL? A: Five minutes in the penalty box 5. Q: What is the Maurice Richard Trophy? A: Given to the player who scores the most goals during the regular season 6. Q: Who is the NHL’s all-time leading goal scorer? A: Wayne Gretzky 7. Q: Who was the first defensemen to win the NHL- point scoring title? A: Bobby Orr 8. Q: Who had the most goals in the 2016-2017 regular season? A: Sidney Crosby 9. Q: What NHL team emerges onto the ice from the giant jaws of a sea beast at home games? A: San Jose Sharks 10. Q: Who is the player to hold the record for most points in one game? A: Darryl Sittler (10 points, in one game – 6 g, 4 a) 11. Q: Which team holds the record for most goals scored in one game? A: Montreal Canadians (16 goals in 1920) 12. Q: Which team won 4 Stanley Cups in a row? A: New York Islanders 13. Q: Who had the most points in the 2016-2017 regular season? A: Connor McDavid 14. Q: Who had the best GAA average in the 2016-2017 regular season? A: Sergei Bobrovsky, GAA 2.06 (HINT: Columbus Blue Jackets) 15.