Contribution to the Analysis of the Predissociated Rovibronic Structure
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Cretaceous Corals from the Bisbee Group (Sonora; Late Barremian - Early Albian): Solenocoeniidae
Cretaceous corals from the Bisbee Group 13 Paleontología Mexicana Volumen 4, núm. 2, 2015, p. 13-24 The Cretaceous corals from the Bisbee Group (Sonora; Late Barremian - Early Albian): Solenocoeniidae Hannes Lösera,* a Instituto de Geología, Estación Regional del Noroeste, Universidad Nacional Autónoma de México, Blvd. L. D. Colosio S/N y Madrid, Col. Los Arcos, 83250 Hermosillo, Sonora, México. * [email protected] Abstract The current work constitutes the third part of the systematic revision about the corals from the Bisbee Group (Late Barremian to Early Albian) and deals with the Solenocoeniidae. This family taxon is applied instead of the poorly defined Cyathophoridae. The family has three genera in the Cretaceous of Sonora: Confusaforma, Cryptocoenia, and Cyathophoropsis. To distinguish samples within the Sonoran fauna and species of this genus, systematic measurements of the corals were taken and statistically analysed. From the Bisbee Group, two Confusaforma, six Cryptocoenia, and one Cyathophoropsis species are here described and illustrated. Most are common Early Cretaceous species with a wide geographic and stratigraphic distribution. Keywords: corals, Scleractinia, Early Cretaceous, Bisbee Group. Resumen El presente trabajo constituye la tercera parte de la revisión sistemática de los corales del Grupo Bisbee (Barremiano temprano a Aptiano tardío), la cual trata sobre la familia Solenocoeniidae, que se ha aplicado en lugar de la familia Cyathophoridae la cual se encuentra mal definida. La familia tiene tres géneros en el Cretácico de Sonora: Confusaforma, Cryptocoenia y Cyathophoropsis. Para distinguir las muestras dentro de la fauna y las especies del género se hicieron mediciones sistemáticas de los corales y se analizaron estadísticamente. -

Care Robots for an Over-Aging Society: a Technical Solution for Japan’S Demographic Problem?
Care Robots for an Over-Aging Society: A Technical Solution for Japan’s Demographic Problem? Martin RATHMANN ([email protected]) Cluster of Excellence “Asia and Europe in a Global Context”, Heidelberg University Abstract Japan has the world's longest life expectancy and highest proportion of older people in its population. As a result, the delivery of old-age care is becoming an urgent and high priority issue for the Japanese government. There is a high demand for care within a society whose population is constantly aging, and within this discrepancy, we have to somehow find a balance. Since the fertility and immigration rates are too low to compensate for the labor shortage, other solutions have to be found for providing care and for sustaining economic power. Japan is known for being a technology-loving country. Since the Meiji restoration (1868-1912), change has been connected with technology. During the period of rapid economic growth, the labor shortage was mainly compensated for by the implementation of industrial robots. There seems to be a positive relationship to technology that goes so far back that the Ministry of Economy, Trade and Industry (METI) is considering robotics as a possible technical solution for Japan’s social and economic problems that emerged from its demographic transition. After having a closer look at the origins of robots and their cultural embedment in Japan, there will be an examination of robot development for home usage, health and old-age care. Taking a closer look on Japan’s robotic landscape will uncover a variety of developments, e.g. -

JDBU Vol 25 No 1
(4. A CLASS BY iV.il Avu DCIV iLJ'.Ctj- m. %: a A •ACKj : %. T/ic Dutch in Ceylon 11. Genoa logy of tlio Schavonguivol Family 4. AIi Muid Geueva f Msefci ng , iJishijp Uouu lluokmoyer. o.s.i;. G. OhiLuufv 1. i'MiLoriai Notes ... [ _.\U pJunfcs on j ORNAMEH Contributions are invited from members on subjects calculated to be of ■interest to the Union. 2LISS. must be written on one. si-it. { Furthei ' of (he paper only and must, reach the ftditor at least a fortnight before, the date of p ub lie a lion oj tin: 'lion ixs. 51- per annum., post . I free. Single copies, if available, 2te. .(SO to be V.B.U. flail. Journal of the - Dutch Burgher Union of Ceylon. ||^.;yVOL.\XXVj; ■. JULY, 1935."' .[No. 1." "l*.. V THE SEVEN KORALES. C To most people of the present day, the words forming the title ^w- iv\ of this article will convey no meaning whatsoever, but in the early yjfflw i>UVwM»*'okW*t> mvvijW.fyg l««wK><&irth&uf days.of British rule they were pregnant with significance. They sTluiinL'W ci>nrfi*tulAtiui« (i> ^WrL ajfrtiiH *>a tni* !»App(^i _. connoted hot only the district which is now known as Kurunegala, l^VkAiiWR « tkij . itwt c-ulnlfti **f iiwir CwVtvAtlOf*--^ £ " \*» -' but they were also associated in men's minds with the dreaded sickness known as "jungle fever." The Seven Korales was one of tkfliV lonaA Mid «iutifi*I A'iurAnca of JeyuKfMt; Atvdj,.^ a.^^ $ t$™rfti»tfti £fAu iktfjt m>« pU'A« t'od tang fe—~; T>^Ev the eleven Provinces which constituted the dominion known under ^pf«**fW! J>keir s£*j*»tw* iiv (width. -

Kandy Kadawathsathara and Gangawata Korale Pradeshiya Sabha Kandy District
Kandy Kadawathsathara and Gangawata Korale Pradeshiya Sabha Kandy District ------------------------------------------------------------------------------------- 1. Financial Statements -------------------------- 1.1 Presentation of Financial Statements -------------------------------------------------- Financial Statements for the year under review had been submitted to the Audit on 29 March 2016 while Financial Statements relating to the preceding year had been submitted on 07 April 2015, and the Auditor General’s Report relating to the year under review was issued to the Secretary of the Sabha on 16 August 2016. 1.2 Qualified Opinion ------------------------ In my opinion except for the effect on the matters described in paragraph 1.3 of this report, financial statements give a true and fair view of the financial position of the Kandy Kadawathsathara and Gangawata Korale Pradeshiya Sabha as at 31 December 2015 and its financial performance for the year then ended in accordance with generally accepted accounting principles. 1.3 Comments on Financial Statements ------------------------------------------------- 1.3.1 Accounting Deficiencies --------------------------------- Following matters were observed. (a) Motor Vehicle No. WPPF – 7488 valued at Rs. 6,390,000 had not been disclosed in notes to the account which had been given to the Sabha in the year 2014 by the Ministry of Local Government and Provincial Council, however the ownership had not been transferred (b) The documents to verify the ownership had not been available with regard to 19 lands mention in the land register maintained by the Sabha, actions had not been taken to verify of those lands and to account by assessing the value 1.3.2 Non-reconciled Control Accounts ------------------------------------------------ As per the schedule, the Staff Loans as at 31 December year under review was Rs. -

MEAL Coordinator - Kandy AP- GIK Ganga Ihala Korale
MEAL Coordinator - Kandy AP- GIK Ganga Ihala Korale Location: [Asia & Pacific] [Sri Lanka] Town/City: Kandy Category: Programme Effectiveness World Vision is a Christian relief, development and advocacy organisation working with children, families and communities to overcome poverty and injustice. World Vision is dedicated to working with the world’s most vulnerable people regardless of their religion, caste, gender or ethnicity. World Vision has been in Sri Lanka since 1977 working in relief and development projects in 20 districts across the country. At World Vision we are passionate about children and are committed to bringing fullness of life to the most vulnerable and disadvantaged. Every day for forty years, that is what our team at World Vision has been doing. We are looking for dynamic individuals to join us on our journey of caring. Monitoring, Evaluation, Accountability & Learning (MEAL) Coordinator Location – Ganga Ihala Korale – GIK (Kandy Area Program) Job Profile The Monitoring & Evaluation , Accountability and Learning Coordinator(MEAL ), will provide technical support to the Area Program(AP) & the Area Development Program(ADP) in developing a strong MEAL System in the areas of monitoring, evaluation, accountability & learning for the design & implementation of quality programs/projects. Reporting to the AP/ADP Manager with technical oversight from the Design Monitoring & Evaluation (DME) Specialist,the job holder will work in collaboration with the field staff/other stakeholders in Page 1/4 developing an efficient & effective MEAL framework & plan that responds to strategic program planning, monitoring & learning agenda of WVL & it’s goals & objectives Based in the AP/ADP Office the MEAL Coordinator is responsible for collecting & mapping project and program data from the field according to the set M&E plans and process the data collected into usable formats for analysis to generate high quality evidence base for learning, decision making & accountability. -
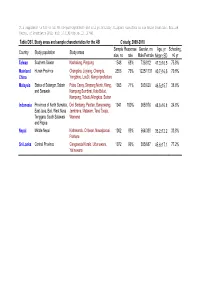
Table DS1. Study Areas and Sample Characteristics for the AB C Study
Table DS1. Study areas and sample characteristics for the AB C study, 2009-2010 Sample Response Gender, no Age, yr Schooling, Country Study population Study areas size, no rate Male/Female MeanSD >6 yr Taiwan Southern Taiwan Kaohsiung, Pingtung 1548 68% 736/812 47.316.5 75.8% Mainland Hunan Province Changsha, Liuyang, Changde, 2356 79% 1225/1131 40.716.5 79.8% China Yongzhou, LouDi, Xiangxi prefecture Malaysia States of Selangor, Sabah Pulau Carey, Simpang Morib, Klang, 1003 71% 383/620 46.515.7 38.8% and Sarawak Kampung Sembirai, Kota Belud, Kampung, Tebedu/Mongkos, Serian Indonesia Provinces of North Sumatra, Deli Serdang, Pacitan, Banyuwangi, 1941 100% 965/976 48.816.8 24.8% East Java, Bali, West Nusa Jembrana, Mataram, Tana Toraja, Tenggara, South Sulawesi Wamena and Papua Nepal Middle Nepal Kathmandu, Chitwan, Nawalparasi, 1002 99% 664/338 35.212.2 33.8% Pokhara Sri Lanka Central Province Gangawata Korale, Udunuwara, 1072 99% 385/687 45.617.1 77.2% Yatinuwara Table DS2. Definition for environmental accessibility and preventive activities in regard to betel-quid (BQ) use in six Asian communities Conditions Definition for Yes Environmental accessibility BQ can be purchased within 1km of the household. 1. Easy availability BQ can be purchased within 1km of the household. 2. Low cost The price for per BQ is less than 0.5 US dollar. 3. Readymade packaging BQ is prepared and packed beforehand in easy use way. 4. Attractive packaging BQ packaging is made in colorful packages and sweet variety. 5. Aggressive marketing Carry out alluring activities or promotive actions for BQ marketing. -

Global Conference on Small-Scale Fisheries Securing Sustainable Small-Scale Fisheries: Bringing Together Responsible Fisheries and Social Development
FAO Fisheries and Aquaculture Report No. 911 FAO, Rapport sur les pêches et l’aquaculture no 911 FAO, Informe de Pesca y Acuicultura No 911 FIEP/R911 (Tri) ISSN 2070-6987 Report of the GLOBAL CONFERENCE ON SMALL-SCALE FISHERIES SECURING SUSTAINABLE SMALL-SCALE FISHERIES: BRINGING TOGETHER RESPONSIBLE FISHERIES AND SOCIAL DEVELOPMENT Bangkok, Thailand, 13–17 October, 2008 Rapport de la CONFÉRENCE MONDIALE SUR LES PÊCHES ARTISANALES POUR UNE PÊCHE ARTISANALE DURABLE: ASSOCIER LA PÊCHE RESPONSABLE AU DÉVELOPPEMENT SOCIAL Bangkok, Thaïlande, 13-17 octobre, 2008 Informe de la CONFERENCIA MUNDIAL SOBRE LA PESCA EN PEQUEÑA ESCALA GARANTIZAR LA PESCA EN PEQUEÑA ESCALA: PESCA RESPONSABLE Y DESARROLLO SOCIAL UNIDOS Bangkok, Tailandia, 13-17 de octubre de 2008 Copies of FAO publications can be requested from: Sales and Marketing Group Communication Division FAO Viale delle Terme di Caracalla 00153 Rome, Italy E-mail: [email protected] Fax: +39 06 57053360 Web site: www.fao.org Les commandes de publications de la FAO peuvent être adressées au: Groupe des ventes et de la commercialisation Division de la communication FAO Viale delle Terme di Caracalla 00153 Rome, Italie Courriel: [email protected] Télécopie: +39 06 57053360 Site Web: www.fao.org Los pedidos de publicaciones de la FAO pueden ser dirigidos a: Grupo de Ventas y Comercialización División de Comunicación FAO Viale delle Terme di Caracalla 00153 Roma, Italia Correo electrónico: [email protected] Fax: +39 06 57053360 Sitio Web: www.fao.org FAO Fisheries and Aquaculture -

A Handbook of the Dipterocarpaceae of Sri Lanka
YAYASAN TUMBUH-TUMBUHAN YANG BERGUNA FOUNDATION FOR USEFUL PLANTS OF TROPICAL ASIA VOLUME III A HANDBOOK OF THE DIPTEROCARPACEAE OF SRI LANKA YAYASAN TUMBUH-TUMBUHAN YANG BERGUNA FOUNDATION FOR USEFUL PLANTS OF TROPICAL ASIA VOLUME III A HANDBOOK OF THE DIPTEROCARPACEAE OF SRI LANKA A.J.G.H. KOSTERMANS Wildlife Heritage Trust of Sri Lanka A HAND BOOK OF THE DIPTEROCARPACEAE OF SRI LANKA A.J.G.H Kostermans Copyright © 1992 by the Wildlife Heritage Trust of Sri Lanka ISBN 955-9114-05-0 All rights reserved. No part of this work covered by the copyright hereon may be reproduced or used in any form or by any means — graphic, electronic or mechanical, including photocopying or information storage and retrieval systems — without permission of the publisher. Manufactured in the Republic of Indonesia Published by the Wildlife Heritage Trust of Sri Lanka, Colombo 8, Sri Lanka Printed by PT Gramedia, Jakarta under supervision of PT Gramedia Pustaka Utama (Publisher), Jakarta 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 CONTENTS Preface 1 Acknowledgments 3 List of illustrations 5 Introduction 8 History of taxonomy 19 Ecology and vegetation classification 22 Dipterocarpaceae and key to the genera 27 Species 29 References 137 Abbreviations 147 Collector's numbers 147 Index of vernacular names 149 Index of scientific names 149 PREFACE Since the publication of P. Ashton's revision of the Dipterocarpaceae of Sri Lanka in 1977 (reprinted in 1980), a fair number of changes have appeared in this family, a large number of new species has been published in periodicals not always easily accessible and, hence, we thought it appropriate to bring together in a single volume an up-to-date overview of the family in Sri Lanka. -

MORALE in PUBLIC EDUCATION a Thesis Presented
PROMOTDlG :MORALE IN PUBLIC EDUCATION A Thesis Presented for the Degree ot Kaster ot Arts by Harvey Eugene Badertscher, B. s. \I THE OHIO STATE UNIVERSITY 1947 Approved by~ ' . TABLE OF CONTENTS CHAPTER PAGE I. INTRODUCTION 1 II. KORALE AND ITS ACHJE1iEMENT 5 m. PROMOT'ING STUDENT MORALE 29 IV. PROMOTING TEACHER MORALE 52 V. PRO}f:OTING CODUNITY MORAIB 79 V:I. EVALUATING MORALE 112 vn. SUDARY 137 BIBLIOGRAPHY 142 CHAPTER I THE TERM "MORALE" In American life morale ia a word which has come into general use only within the last several years. The word first appfared in titles of American periodical lit erature in 1918 toward the close of the first World War. In that year Readers' Guide to Periodical Literature listed two titles on morale, and in 1919 two more were listed. Then in t~~ period trom 1920 to 1940 o~ly ten articles on morale were listed. Yt can thus be seen that tor the two deoades following World War I the term was almost forgotten. With the outbreak of World War II, and especially in connection with the tall ot France, morale became an im portant word in American thinking, writing, and discussion. It appeared ~ billboard posters, in the daily papers, in . l . all kinds of advertising, in educational periodicals, in connection with industry, and in describing the condition of our armed forces at home and overseas, as well as con- ditions on the home front. Many committees were organized to promote morale in one torm or another. Ill 1942 alone, over 150 articles were listed under the heading of "morale" in Readers' Guide to Periodical Literature. -

Impact of Global Value Chains on Performance
ADBI Working Paper Series IMPACT OF GLOBAL VALUE CHAINS ON PERFORMANCE OF SMALL AND MEDIUM-SIZED ENTERPRISES IN SRI LANKA: EVIDENCE FROM SRI LANKA N.P. Ravindra Deyshappriya and B. C. H. Maduwanthi No. 1153 June 2020 Asian Development Bank Institute N.P. Ravindra Deyshappriya is a senior lecturer at the Faculty of Management of Uva Wellassa University of Sri Lanka. B. C. H. Maduwanthi is a lecturer at the Faculty of Agriculture of Uva Wellassa University of Sri Lanka. The views expressed in this paper are the views of the author and do not necessarily reflect the views or policies of ADBI, ADB, its Board of Directors, or the governments they represent. ADBI does not guarantee the accuracy of the data included in this paper and accepts no responsibility for any consequences of their use. Terminology used may not necessarily be consistent with ADB official terms. Working papers are subject to formal revision and correction before they are finalized and considered published. The Working Paper series is a continuation of the formerly named Discussion Paper series; the numbering of the papers continued without interruption or change. ADBI’s working papers reflect initial ideas on a topic and are posted online for discussion. Some working papers may develop into other forms of publication. Suggested citation: Deyshappriya, N.P. R. and B. C. H. Maduwanthi. 2020. Impact of Global Value Chains on Performance of Small and Medium-Sized Enterprises in Sri Lanka: Evidence from Sri Lanka. ADBI Working Paper 1153. Tokyo: Asian Development Bank Institute. Available: https://www.adb.org/publications/impact-global-value-chains-performance-smse-sri-lanka Please contact the authors for information about this paper. -

Gender and Labour Migration A
While IOM endeavours to ensure the accuracy and completeness of the content of this paper, the views, findings, interpretations and conclusions expressed herein are those of the authors and field researchers and do not necessarily reflect the official position of the IOM and their Member States. IOM does not accept any liability for any loss which may arise from the reliance on information contained in this paper. IOM is committed to the principle that humane and orderly migration benefits migrants and society. As an intergovernmental organization, IOM acts with its partners in the international community to: assist in meeting the operational challenges of migration; advance understanding of migration issues; encourage social and economic development through migration; and uphold the human dignity and well-being of migrants. International Organization for Migration 17 route des Morillons 1211 Geneva 19 Switzerland Tel: +41.22.717 91 11 Fax: +41.22.798 61 50 E-mail: [email protected] Internet: http://www.iom.int ISBN 978-92-9068-453-4 © 2009 International Organization for Migration (IOM) All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise without the prior written permission of the publisher. 21_09 Gender Labour Migration in Asia Gender and Labour Migration in Asia Contents Foreword .................................................................................................. 7 Introduction -

Threatened Birds of Asia: the Birdlife International Red Data Book
Threatened Birds of Asia: The BirdLife International Red Data Book Editors N. J. COLLAR (Editor-in-chief), A. V. ANDREEV, S. CHAN, M. J. CROSBY, S. SUBRAMANYA and J. A. TOBIAS Maps by RUDYANTO and M. J. CROSBY Principal compilers and data contributors ■ BANGLADESH P. Thompson ■ BHUTAN R. Pradhan; C. Inskipp, T. Inskipp ■ CAMBODIA Sun Hean; C. M. Poole ■ CHINA ■ MAINLAND CHINA Zheng Guangmei; Ding Changqing, Gao Wei, Gao Yuren, Li Fulai, Liu Naifa, Ma Zhijun, the late Tan Yaokuang, Wang Qishan, Xu Weishu, Yang Lan, Yu Zhiwei, Zhang Zhengwang. ■ HONG KONG Hong Kong Bird Watching Society (BirdLife Affiliate); H. F. Cheung; F. N. Y. Lock, C. K. W. Ma, Y. T. Yu. ■ TAIWAN Wild Bird Federation of Taiwan (BirdLife Partner); L. Liu Severinghaus; Chang Chin-lung, Chiang Ming-liang, Fang Woei-horng, Ho Yi-hsian, Hwang Kwang-yin, Lin Wei-yuan, Lin Wen-horn, Lo Hung-ren, Sha Chian-chung, Yau Cheng-teh. ■ INDIA Bombay Natural History Society (BirdLife Partner Designate) and Sálim Ali Centre for Ornithology and Natural History; L. Vijayan and V. S. Vijayan; S. Balachandran, R. Bhargava, P. C. Bhattacharjee, S. Bhupathy, A. Chaudhury, P. Gole, S. A. Hussain, R. Kaul, U. Lachungpa, R. Naroji, S. Pandey, A. Pittie, V. Prakash, A. Rahmani, P. Saikia, R. Sankaran, P. Singh, R. Sugathan, Zafar-ul Islam ■ INDONESIA BirdLife International Indonesia Country Programme; Ria Saryanthi; D. Agista, S. van Balen, Y. Cahyadin, R. F. A. Grimmett, F. R. Lambert, M. Poulsen, Rudyanto, I. Setiawan, C. Trainor ■ JAPAN Wild Bird Society of Japan (BirdLife Partner); Y. Fujimaki; Y. Kanai, H.