Carnevale Et Al. 1.1 Mb
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Observation of Rip Currents by Synthetic Aperture Radar
OBSERVATION OF RIP CURRENTS BY SYNTHETIC APERTURE RADAR José C.B. da Silva (1) , Francisco Sancho (2) and Luis Quaresma (3) (1) Institute of Oceanography & Dept. of Physics, University of Lisbon, 1749-016 Lisbon, Portugal (2) Laboratorio Nacional de Engenharia Civil, Av. do Brasil, 101 , 1700-066, Lisbon, Portugal (3) Instituto Hidrográfico, Rua das Trinas, 49, 1249-093 Lisboa , Portugal ABSTRACT Rip currents are near-shore cellular circulations that can be described as narrow, jet-like and seaward directed flows. These flows originate close to the shoreline and may be a result of alongshore variations in the surface wave field. The onshore mass transport produced by surface waves leads to a slight increase of the mean water surface level (set-up) toward the shoreline. When this set-up is spatially non-uniform alongshore (due, for example, to non-uniform wave breaking field), a pressure gradient is produced and rip currents are formed by converging alongshore flows with offshore flows concentrated in regions of low set-up and onshore flows in between. Observation of rip currents is important in coastal engineering studies because they can cause a seaward transport of beach sand and thus change beach morphology. Since rip currents are an efficient mechanism for exchange of near-shore and offshore water, they are important for across shore mixing of heat, nutrients, pollutants and biological species. So far however, studies of rip currents have mainly relied on numerical modelling and video camera observations. We show an ENVISAT ASAR observation in Precision Image mode of bright near-shore cell-like signatures on a dark background that are interpreted as surface signatures of rip currents. -

Part III-2 Longshore Sediment Transport
Chapter 2 EM 1110-2-1100 LONGSHORE SEDIMENT TRANSPORT (Part III) 30 April 2002 Table of Contents Page III-2-1. Introduction ............................................................ III-2-1 a. Overview ............................................................. III-2-1 b. Scope of chapter ....................................................... III-2-1 III-2-2. Longshore Sediment Transport Processes ............................... III-2-1 a. Definitions ............................................................ III-2-1 b. Modes of sediment transport .............................................. III-2-3 c. Field identification of longshore sediment transport ........................... III-2-3 (1) Experimental measurement ............................................ III-2-3 (2) Qualitative indicators of longshore transport magnitude and direction ......................................................... III-2-5 (3) Quantitative indicators of longshore transport magnitude ..................... III-2-6 (4) Longshore sediment transport estimations in the United States ................. III-2-7 III-2-3. Predicting Potential Longshore Sediment Transport ...................... III-2-7 a. Energy flux method .................................................... III-2-10 (1) Historical background ............................................... III-2-10 (2) Description ........................................................ III-2-10 (3) Variation of K with median grain size................................... III-2-13 (4) Variation of K with -

OCEANS ´09 IEEE Bremen
11-14 May Bremen Germany Final Program OCEANS ´09 IEEE Bremen Balancing technology with future needs May 11th – 14th 2009 in Bremen, Germany Contents Welcome from the General Chair 2 Welcome 3 Useful Adresses & Phone Numbers 4 Conference Information 6 Social Events 9 Tourism Information 10 Plenary Session 12 Tutorials 15 Technical Program 24 Student Poster Program 54 Exhibitor Booth List 57 Exhibitor Profiles 63 Exhibit Floor Plan 94 Congress Center Bremen 96 OCEANS ´09 IEEE Bremen 1 Welcome from the General Chair WELCOME FROM THE GENERAL CHAIR In the Earth system the ocean plays an important role through its intensive interactions with the atmosphere, cryo- sphere, lithosphere, and biosphere. Energy and material are continually exchanged at the interfaces between water and air, ice, rocks, and sediments. In addition to the physical and chemical processes, biological processes play a significant role. Vast areas of the ocean remain unexplored. Investigation of the surface ocean is carried out by satellites. All other observations and measurements have to be carried out in-situ using research vessels and spe- cial instruments. Ocean observation requires the use of special technologies such as remotely operated vehicles (ROVs), autonomous underwater vehicles (AUVs), towed camera systems etc. Seismic methods provide the foundation for mapping the bottom topography and sedimentary structures. We cordially welcome you to the international OCEANS ’09 conference and exhibition, to the world’s leading conference and exhibition in ocean science, engineering, technology and management. OCEANS conferences have become one of the largest professional meetings and expositions devoted to ocean sciences, technology, policy, engineering and education. -

Rip Currents and Alongshore Flows in Single Channels Dredged in the Surf
PUBLICATIONS Journal of Geophysical Research: Oceans RESEARCH ARTICLE Rip currents and alongshore flows in single channels dredged 10.1002/2016JC012222 in the surf zone Key Points: Melissa Moulton1,2 , Steve Elgar2 , Britt Raubenheimer2 , John C. Warner3 , and Rip currents, feeder currents, and Nirnimesh Kumar4 meandering alongshore currents were observed in single channels 1 2 dredged in the surf zone Applied Physics Laboratory, University of Washington, Seattle, Washington, USA, Department of Applied Ocean Physics 3 The model COAWST reproduces the and Engineering, Woods Hole Oceanographic Institution, Woods Hole, Massachusetts, USA, United States Geological observed circulation patterns, and is Survey, Coastal and Marine Geology Program, Woods Hole, Massachusetts, USA, 4Department of Civil and Environmental used to investigate dynamics for a Engineering, University of Washington, Seattle, Washington, USA wider range of conditions A parameter based on breaking-wave-driven setup patterns and alongshore currents predicts Abstract To investigate the dynamics of flows near nonuniform bathymetry, single channels (on average offshore-directed flow speeds 30 m wide and 1.5 m deep) were dredged across the surf zone at five different times, and the subsequent evolution of currents and morphology was observed for a range of wave and tidal conditions. In addition, Correspondence to: circulation was simulated with the numerical modeling system COAWST, initialized with the observed M. Moulton, incident waves and channel bathymetry, and with an extended set of wave conditions and channel [email protected] geometries. The simulated flows are consistent with alongshore flows and rip-current circulation patterns observed in the surf zone. Near the offshore-directed flows that develop in the channel, the dominant terms Citation: Moulton, M., S. -

1D Laboratory Study on Wave-Induced Setup Over A
1 LES Modeling of Tsunami-like Solitary Wave Processes 2 over Fringing Reefs 3 4 Yu Yao1, 4, Tiancheng He1, Zhengzhi Deng2*, Long Chen1, 3, Huiqun Guo1 5 6 1 School of Hydraulic Engineering, Changsha University of Science and Technology, 7 Changsha, Hunan 410114, China. 8 2 Ocean College, Zhejiang University, Zhoushan, Zhejiang 316021, China. 9 3 Key Laboratory of Water-Sediment Sciences and Water Disaster Prevention of 10 Hunan Province, Changsha 410114, China. 11 4Key Laboratory of Coastal Disasters and Defence of Ministry of Education, 12 Nanjing, Jiangsu 210098, China 13 14 15 16 * Corresponding author: Zhengzhi Deng 17 E-mail: [email protected] 18 Tel: +86 15068188376 19 1 20 ABSTRACT 21 Many low-lying tropical and sub-tropical reef-fringed coasts are vulnerable to 22 inundation during tsunami events. Hence accurate prediction of tsunami wave 23 transformation and runup over such reefs is a primary concern in the coastal management 24 of hazard mitigation. To overcome the deficiencies of using depth-integrated models in 25 modeling tsunami-like solitary waves interacting with fringing reefs, a three-dimensional 26 (3D) numerical wave tank based on the Computational Fluid Dynamics (CFD) tool 27 OpenFOAM® is developed in this study. The Navier-Stokes equations for two-phase 28 incompressible flow are solved, using the Large Eddy Simulation (LES) method for 29 turbulence closure and the Volume of Fluid (VOF) method for tracking the free surface. 30 The adopted model is firstly validated by two existing laboratory experiments with 31 various wave conditions and reef configurations. The model is then applied to examine 32 the impacts of varying reef morphologies (fore-reef slope, back-reef slope, lagoon width, 33 reef-crest width) on the solitary wave runup. -

A Liminal Experience Under the Surface of the Ocean
UNIVERSIDADE DE LISBOA FACULDADE DE BELAS-ARTES APNEA A liminal experience under the surface of the ocean Janna Nadjejda Ribow Guichet Dissertação Mestrado em Arte Multimedia Especialização em Fotografia Dissertação orientada pela Professora Doutora Maria João Pestana Noronha Gamito 2021 DECLARAÇÃO DE AUTORIA Eu Janna Nadjejda Ribow Guichet, declaro que a presente dissertação de mestrado intitulada “Apnéia”, é o resultado da minha investigação pessoal e independente. O conteúdo é original e todas as fontes consultadas estão devidamente mencionadas na bibliografia ou outras listagens de fontes documentais, tal como todas as citações diretas ou indiretas têm devida indicação ao longo do trabalho segundo as normas académicas. O Candidato [assinatura] Lisboa, 27.10.19 RESUMO O trabalho é sobre uma imersão no oceano e em nós mesmos. A questão é: como podemos obter um efeito positivo por meio do oceano? O primeiro capítulo analisará os pensamentos antigos e contemporâneos do sublime; A figura do vórtice foi usada nas artes e na literatura para criar sensações sublimes, Immanuel Kant e Edmund Burke afirmaram que o sublime pode trazer um efeito positivo que será discutido. Uma sensação sublime diferente é a Liminalidade, que encontrei durante a Apnéia. Muitos artistas descrevem seu poder transformador, que será comparado à pesquisa médica científica. Mas a mensagem fundamental permanece: “A experiência sublime é fundamentalmente transformadora, sobre a relação entre desordem e ordem, e a ruptura das coordenadas estáveis de tempo e espaço. Algo se precipita e somos profundamente alterados.” (Morley, 2010, p.12) O segundo capítulo define Ambientes Imersivos em Artes e Apnéia. Após a experiência liminar comecei a treinar o desporto e aprendi a controlar minha mente e corpo de forma imersiva, o que trouxe à tona os conceitos: ponto do silêncio (preparação), jogo mental (submersão) e foco (volta a superfície). -

Wave-Breaking Turbulence in the Ocean Surface Layer
JUNE 2016 T H O M S O N E T A L . 1857 Wave-Breaking Turbulence in the Ocean Surface Layer JIM THOMSON,MICHAEL S. SCHWENDEMAN, AND SETH F. ZIPPEL Applied Physics Laboratory, University of Washington, Seattle, Washington SAEED MOGHIMI Oregon State University, Corvallis, Oregon JOHANNES GEMMRICH University of Victoria, Victoria, British Columbia, Canada W. ERICK ROGERS Naval Research Laboratory, Stennis Space Center, Louisiana (Manuscript received 12 July 2015, in final form 17 March 2016) ABSTRACT Observations of winds, waves, and turbulence at the ocean surface are compared with several analytic formulations and a numerical model for the input of turbulent kinetic energy by wave breaking and the subsequent dissipation. The observations are generally consistent with all of the formulations, although some differences are notable at winds greater than 15 m s21. The depth dependence of the turbulent dissipation rate beneath the waves is fit to a decay scale, which is sensitive to the choice of vertical reference frame. In the surface-following reference frame, the strongest turbulence is isolated within a shallow region of depths much less than one significant wave height. In a fixed reference frame, the strong turbulence penetrates to depths that are at least half of the significant wave height. This occurs because the turbulence of individual breakers persists longer than the dominant period of the waves and thus the strong surface turbulence is carried from crest to trough with the wave orbital motion. 1. Introduction Gemmrich and Farmer 2004; Gemmrich 2010). The dynamic balance assumed is that the wave energy lost Wave breaking at the ocean surface limits wave during breaking S becomes a flux of turbulent ki- growth (Melville 1994), enhances gas exchange (Zappa brk netic energy F into the ocean surface layer that is dis- et al. -

Protecting Surf Breaks and Surfing Areas in California
Protecting Surf Breaks and Surfing Areas in California by Michael L. Blum Date: Approved: Dr. Michael K. Orbach, Adviser Masters project submitted in partial fulfillment of the requirements for the Master of Environmental Management degree in the Nicholas School of the Environment of Duke University May 2015 CONTENTS ACKNOWLEDGEMENTS ........................................................................................................... vi LIST OF FIGURES ...................................................................................................................... vii LIST OF TABLES ........................................................................................................................ vii LIST OF ACRONYMS ............................................................................................................... viii LIST OF DEFINITIONS ................................................................................................................ x EXECUTIVE SUMMARY ......................................................................................................... xiii 1. INTRODUCTION ...................................................................................................................... 1 2. STUDY APPROACH: A TOTAL ECOLOGY OF SURFING ................................................. 5 2.1 The Biophysical Ecology ...................................................................................................... 5 2.2 The Human Ecology ............................................................................................................ -

Questions Breaking Waves
Introduction to Oceanography Midterm 2: November 20 (Monday) Review session: Friday, Nov. 17 (TODAY!) 4:00-5:00pm in Franz 1260. Extra credit video screening: Monday, Nov. 20, 4:00-5:00pm in Royce 190. Coast Guard vessel training in breaking waves. Video by U.S. Coast Guard Air Lecture 20: Breaking Waves, Tsunami, Tides Station Cape Cod. Public Domain https://www.facebook.com/USCo Breaking wave and surfer at Mavericks, near Half Moon Bay, California. Photo by Shalom Jacobovitz, astGuardNortheast/videos/10153 Creative Commons Attribution-Share Alike 2.0 Generic, 597379234398/ https://commons.wikimedia.org/wiki/File:2010_mavericks_competition_edit1.jpg The Anatomy of a Wave The Dynamics of a Wave Wave Period – time between crests Wave Frequency – number of crests per second Wave Speed – rate crests move (meters/second) Animation courtesy Dr. Dan Russell, Kettering University, http://paws.kettering.edu/~d russell/Demos/wave-x- t/wave-x-t.html Period, frequency, speed and wavelength are related! Remember These! Period = 1/frequency Adapted from figure by Kraaiennest, Wikimedia Commons, Creative Commons A S-A 3.0, http://commons.wikimedia.org/wiki/File:Sine_wave_amplitude.svg Speed = wavelength / period = wavelength x frequency Questions Breaking Waves NASA/JPL, Public Domain, http://www.meted.ucar.edu/EUME TSAT/jason/media/graphics/tp_wi nd_wave_janjun1995.jpg Teahupoo, Tahiti, Photo by Duncan Rawlinson, Creative Commons A 2.0 Generic, http://thelastminuteblog.com/photos/album/72157603098986701/photo/1973927918/teahupoo-surfing-november- 2-2007- 1 Waves can’t transport energy as efficiently in shallow water When Do Waves Break? Waves start to break when: – The angle between front & backside of wave < 120 degrees – This occurs when Height > 1/7 Wavelength – Typically when Height ~3/4 water Depth aokomoriuta, Wikimedia Commons, Creative Commons A S-A 3.0, R. -

Safety Check List Easthamptonoceanrescue.Org Ubs
Safety Check List • Listen to surf forecast • Watch You Tube video of rip currents in action • Check for warning signs and flags • Scan water for visible rips & wave conditions from highest vintage point • Swim near lifeguard if available ubs.com eas thamptonoceanrescue.org E • L • I • C • C • A Eastern Long Island Coastal Conservation Alliance, Ltd. UNDERSTANDING WAVES AND CURRENTS Your Life May Depend Upon It Knowledge of waves and currents can help beachgoers be safer at the beach. Big breaking waves that tower over five feet high are too dangerous for most bathers and swimmers, but even relatively small waves (e.g., 2-3 feet) that seem innocuous can generate dangerous rip currents. The Surf Safety Check List helps you read the waves and currents and therefore gauge the situation relative to your own swim - ming ability. Skilled surfers seek out large plunging breakers for the most spectacular rides, and often utilize strong offshore-flowing currents (e.g., rip currents) to propel themselves seaward so they can catch the next wave. Surfers have the advantage of having a flotation device (e.g., surfboard) so that they are much better prepared than swimmers to deal with ocean forces, but even these thrill seekers must understand and respect the power of the sea. A typical summer day at Ditch Plains Beach where rip currents may be present but are not always apparent. SURF SAFETY CHECK LIST • Listen to the surf forecast. • Watch videos of rip currents in action on YouTube (www.ripcurrents.com) before heading to the beach. • Know your location in the event of an emergency; some beach accesses are numbered, while others are named by the road ending or landmarks. -
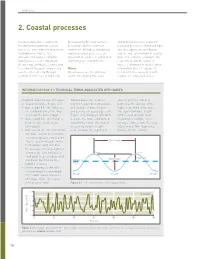
2. Coastal Processes
CHAPTER 2 2. Coastal processes Coastal landscapes result from by weakening the rock surface and driving nearshore sediment the interaction between coastal to facilitate further sediment transport processes. Wind and tides processes and sediment movement. movement. Biological, biophysical are also significant contributors, Hydrodynamic (waves, tides and biochemical processes are and are indeed dominant in coastal and currents) and aerodynamic important in coral reef, salt marsh dune and estuarine environments, (wind) processes are important. and mangrove environments. respectively, but the action of Weathering contributes significantly waves is dominant in most settings. to sediment transport along rocky Waves Information Box 2.1 explains the coasts, either directly through Ocean waves are the principal technical terms associated with solution of minerals, or indirectly agents for shaping the coast regular (or sinusoidal) waves. INFORMATION BOX 2.1 TECHNICAL TERMS ASSOCIATED WITH WAVES Important characteristics of regular, Natural waves are, however, wave height (Hs), which is or sinusoidal, waves (Figure 2.1). highly irregular (not sinusoidal), defined as the average of the • wave height (H) – the difference and a range of wave heights highest one-third of the waves. in elevation between the wave and periods are usually present The significant wave height crest and the wave trough (Figure 2.2), making it difficult to off the coast of south-west • wave length (L) – the distance describe the wave conditions in England, for example, is, on between successive crests quantitative terms. One way of average, 1.5m, despite the area (or troughs) measuring variable height experiencing 10m-high waves • wave period (T) – the time from is to calculate the significant during extreme storms. -

Observations of a Rip Current System
Calhoun: The NPS Institutional Archive Faculty and Researcher Publications Faculty and Researcher Publications 2005 RIPEX: Observations of a rip current system MacMahan, Jamie H. þÿMarine Geology, Vol. 218, (2005), pp. 113 134 http://hdl.handle.net/10945/45737 Marine Geology 218 (2005) 113–134 www.elsevier.com/locate/margeo RIPEX: Observations of a rip current system Jamie H. MacMahana,T, Ed B. Thorntona, Tim P. Stantona, Ad J.H.M. Reniersb aNaval Postgraduate School, Oceanography Department, Monterey, CA 93943, USA bCivil Engineering and Geosciences, Delft University of Technology, Delft, The Netherlands Received 10 June 2004; received in revised form 23 February 2005; accepted 14 March 2005 Abstract Rip current kinematics and beach morphodynamics were measured for 44 days at Sand City, Monterey Bay, CA using 15 instruments composed of co-located velocity and pressure sensors, acoustic Doppler current profilers, and kinematic GPS surveys. The morphology consisted of a low-tide terrace with incised quasi-periodic rip channels, representative of transverse bars. Offshore (17 m depth) significant wave height and peak period ranged 0.20–3.0 m and 5–20 s. The mean wave direction was consistently near 08 resulting in rip channel morphology, which evolved in response to the changing wave characteristics. An inverse relationship between sediment accreting on the transverse bar and eroding in the rip channel was found. The spatial distribution of sediment is reflected in the background rip current flow field. The mean velocity magnitudes within the rip channel (transverse bars) increased offshore (onshore) with decreasing tidal elevations and increased with increasing sea-swell energy. Eulerian averaged flows were predominantly shoreward on the transverse bars and seaward within the rip channel throughout the experiment, resulting in a persistent cellular circulation, except during low wave energy.