DOCSLIB.ORG

Pulse Compression for Different Types of Radar Signals

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Pulse Compression for Different Types of Radar Signals Thesis no: MCS-2012-09 Pulse compression for different types of radar signals. This thesis is presented as of Bachelor Science in Electrical Engineering with Emphasis on Telecommunication Blekinge Institute of Technology September 2012 Blekinge Institute of Technology School of Engineering Department of Electrical Engineering Supervisor: Mats Pettersson Authors: Tomás Garnacho Aparicio & Alberto Trejo Roldán 2 2 3 Abstract The aim of our project is to compare pulse compression of different waveforms using correlation of real signals or matched filter for analytic signals. In this thesis a set of programs is developed for this comparison. The characteristic of the matched filter is that it processes the highest possible Signal to Noise ratio (SNR) under the assumption of white noise. The implementation of the algorithm is made in Matlab. Radar signal processors are usually carried out over a specified range window. Returns from all targets within the received window are collected and passed through the matched filter to perform the pulse compression. Because of the recent development of digital signal processors (DSPs), this process is often performed digitally. The aim of this work is to get better quality in the radar images, including SAR (Synthetic Aperture Radar) and to explain the characteristics of each waveform. The thesis also includes an appendix, where the implemented programs and program code are attached. The work also aims at illustrative and didactic purposes. The programs have been developed so as to be easily understood and therefore useful for engineering students. 3 4 4 5 Gracias a todos aquellos que me han acompañado en este camino. A mi madre. “Si caes, levántate... si vuelves a caer, levántate otra vez... Y si vuelves a caer levántate una y otra vez... Sólo en la lucha, la fe, la constancia y la fuerza de voluntad llegaremos al triunfo...” “If you fall, get up... If you fall back again, then get up again... and if you fall back once more, get up again and again. In struggle, faith, perseverance and power are the ways to achieve the victory..." Tomás 5 6 6 7 Firstly, I would like to thank to everyone who helped us with our thesis during our stay as exchange students in Blekinge Tekniska Högskola. I especially want to mention our project supervisor Mats Pettersson for his help and support from the very beginning of the project. Furthermore I also want to give thanks to all the classmates I met during my studies as well as all the friends that were not studying with me but giving me their support, though. Additionally I am grateful for meeting so many great persons during my stay, especially Tamara, and I want to thank them for the help they were during my time in Sweden. Finally I want to thank my family, especially my parents and my sister who gave me the possibility to study abroad and their endless support and help. Alberto 7 8 8 9 Table of contents Abstract ................................................................................................................................... 3 Table of contents .................................................................................................................... 9 List of Figures ....................................................................................................................... 11 List of Acronyms .................................................................................................................. 13 Chapter 1 Introduction .......................................................................................................... 15 Chapter 2 Matched Filter ...................................................................................................... 17 2.1. Fundamentals of the Matched Filter................................................................... 17 2.2. Range Resolution Properties .............................................................................. 20 Chapter 3 Analysis Matched Filter Response of Linear Frequency Modulated Waveforms (chirp) ................................................................................................................................... 25 3.1. Basics of Linear FM Waveforms ....................................................................... 25 3.2. Frequency analysis of Linear FM Waveforms ................................................... 27 3.3. Pulse Compression Process ................................................................................ 33 Chapter 4 Cross-Correlation ................................................................................................. 37 Chapter 5 Analytic Signal .................................................................................................... 43 5.1. Definition of Hilbert transforms. ........................................................................ 43 5.2. Analytic Signal Application ............................................................................... 44 Chapter 6 Different types of radar signals ............................................................................ 53 6.1. Binary phase coded pulse ................................................................................... 53 6.2. Square pulse ....................................................................................................... 61 Chapter 7 Conclusions .......................................................................................................... 67 9 10 References ............................................................................................................................ 69 Appendix .............................................................................................................................. 73 Program code ................................................................................................................ 73 10 11 List of Figures Figure 1.Matched Filter maximizes the signal peak to mean noise ratio. ................................................... 20 Figure 2. llustration of a square pulse and its corresponding spectra. ........................................................ 21 Figure 3. Square Pulse compressed ............................................................................................................ 22 Figure 4. Comparison between the ultimate resolution of a rectangular constant frequency and a chirp pulse ................................................................................................................................................. 23 Figure 5. Output pulse compression filter. ................................................................................................. 24 Figure 6. Real part and imaginary part of signal chirp ................................................................................ 26 Figure 7. Signal chirp in the frequency domain by the use of FFT ............................................................... 28 Figure 8. Graphical Representation of signal delay. ................................................................................... 29 Figure 9. Signal chirp delayed in the frequency domain by the use of FFT .................................................. 30 Figure 10. Ramp function to implement the delayed signal. ...................................................................... 31 Figure 11. Comparison of signal chirp and signal chirp delayed in the frequency domain .......................... 32 Figure 12. Comparison of signal chirp and signal chirp delayed in the time domain ................................... 33 Figure 13. Fast Convolution Processor ....................................................................................................... 34 Figure 14. Response in frequency after after the matched filter ................................................................ 35 Figure 15. Output of the matched filter ..................................................................................................... 36 Figure 16. Convolution of Reflected echo and Time reversed pulse ........................................................... 38 Figure 17. Convolution of Reflected echo and Time reversed pulse. Intermediate step ............................. 38 Figure 18. Convolution of Reflected echo and Time reversed pulse. Finished convolution ......................... 39 Figure 19. Matched filter by cross-correlation process ............................................................................... 40 Figure 20. Comparison of the responses of matched filter and cross-correlation process for a transmitted signal ................................................................................................................................................ 41 11 12 Figure 21. Comparison of the envelopes of the responses of matched filter and cross-correlation process for a transmitted signal .................................................................................................................... 42 Figure 22. Real part and imaginary part of analytic signal. Orthogonal vectors .......................................... 44 Figure 23. Analytic signal property Hilbert ................................................................................................. 46 Figure 24. Diagram of the generation of the analytic signal ....................................................................... 47 Figure 25. Comparison between the original chirp signal and the recovered signal ..................................
Load more

Recommended publications
  • Optical Single Sideband for Broadband and Subcarrier Systems
    University of Alberta Optical Single Sideband for Broadband And Subcarrier Systems Robert James Davies 0 A thesis submitted to the faculty of Graduate Studies and Research in partial fulfillrnent of the requirernents for the degree of Doctor of Philosophy Department of Electrical And Computer Engineering Edmonton, AIberta Spring 1999 National Library Bibliothèque nationale du Canada Acquisitions and Acquisitions et Bibliographie Services services bibliographiques 395 Wellington Street 395, rue Wellington Ottawa ON KlA ON4 Ottawa ON KIA ON4 Canada Canada Yom iUe Votre relérence Our iSie Norre reference The author has granted a non- L'auteur a accordé une licence non exclusive licence allowing the exclusive permettant à la National Library of Canada to Bibliothèque nationale du Canada de reproduce, loan, distribute or sell reproduire, prêter, distribuer ou copies of this thesis in microform, vendre des copies de cette thèse sous paper or electronic formats. la forme de microfiche/nlm, de reproduction sur papier ou sur format électronique. The author retains ownership of the L'auteur conserve la propriété du copyright in this thesis. Neither the droit d'auteur qui protège cette thèse. thesis nor substantial extracts fkom it Ni la thèse ni des extraits substantiels may be printed or otheMrise de celle-ci ne doivent être Unprimés reproduced without the author's ou autrement reproduits sans son permission. autorisation. Abstract Radio systems are being deployed for broadband residential telecommunication services such as broadcast, wideband lntemet and video on demand. Justification for radio delivery centers on mitigation of problems inherent in subscriber loop upgrades such as Fiber to the Home (WH)and Hybrid Fiber Coax (HFC).
    [Show full text]
  • Waveform Design and Related Processing for Multiple Target Detection and Resolution Target Detection and Resolution
    DOI: 10.5772/intechopen.71549 Chapter 1 Provisional chapter Waveform Design and Related Processing for Multiple Waveform Design and Related Processing for Multiple Target Detection and Resolution Target Detection and Resolution Gaspare Galati and Gabriele Pavan Gaspare Galati and Gabriele Pavan Additional information is available at the end of the chapter Additional information is available at the end of the chapter http://dx.doi.org/10.5772/intechopen.71549 Abstract The performance of modern radar systems mostly depends on the radiated wave- forms, whose design is the basis of the entire system design. Today’s coherent, solid- state radars (either of the phased array type or of the single-radiator type as air traffic control or marine radars) transmit a set of deterministic signals with relatively large duty cycles, an order of 10%, calling for pulse compression to get the required range resolution. Often, power budget calls for different pulse lengths (e.g., short, medium, and long waveforms with a rectangular envelope) to cover the whole radar range. The first part of the chapter includes the topic of mitigating the effect of unwanted side lobes, inherent to every pulse compression, which is achieved both by a careful and optimal design of the waveform and by a (possibly mismatched) suitable processing. The second part of the chapter deals with the novel noise radar technology, not yet used in commercial radar sets but promising: (1) to prevent radar interception and exploitation by an enemy part and (2) to limit the mutual interferences of nearby radars, as in the marine environment. In this case, the design includes a tailoring of a set of pseudo-random waveforms, generally by recursive processing, to comply with the system requirements.
    [Show full text]
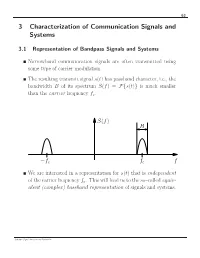
  • 3 Characterization of Communication Signals and Systems
    63 3 Characterization of Communication Signals and Systems 3.1 Representation of Bandpass Signals and Systems Narrowband communication signals are often transmitted using some type of carrier modulation. The resulting transmit signal s(t) has passband character, i.e., the bandwidth B of its spectrum S(f) = s(t) is much smaller F{ } than the carrier frequency fc. S(f) B f f f − c c We are interested in a representation for s(t) that is independent of the carrier frequency fc. This will lead us to the so–called equiv- alent (complex) baseband representation of signals and systems. Schober: Signal Detection and Estimation 64 3.1.1 Equivalent Complex Baseband Representation of Band- pass Signals Given: Real–valued bandpass signal s(t) with spectrum S(f) = s(t) F{ } Analytic Signal s+(t) In our quest to find the equivalent baseband representation of s(t), we first suppress all negative frequencies in S(f), since S(f) = S( f) is valid. − The spectrum S+(f) of the resulting so–called analytic signal s+(t) is defined as S (f) = s (t) =2 u(f)S(f), + F{ + } where u(f) is the unit step function 0, f < 0 u(f) = 1/2, f =0 . 1, f > 0 u(f) 1 1/2 f Schober: Signal Detection and Estimation 65 The analytic signal can be expressed as 1 s+(t) = − S+(f) F 1{ } = − 2 u(f)S(f) F 1{ } 1 = − 2 u(f) − S(f) F { } ∗ F { } 1 The inverse Fourier transform of − 2 u(f) is given by F { } 1 j − 2 u(f) = δ(t) + .
    [Show full text]
  • Design and Application of a Hilbert Transformer in a Digital Receiver
    Proceedings of the SDR 11 Technical Conference and Product Exposition, Copyright © 2011 Wireless Innovation Forum All Rights Reserved DESIGN AND APPLICATION OF A HILBERT TRANSFORMER IN A DIGITAL RECEIVER Matt Carrick (Northrop Grumman, Chantilly, VA, USA; [email protected]); Doug Jaeger (Northrop Grumman, Chantilly, VA, USA; [email protected]); fred harris (San Diego State University, San Diego, CA, USA; [email protected]) ABSTRACT A common method of down converting a signal from an intermediate frequency (IF) to baseband is using a quadrature down-converter. One problem with the quadrature down-converter is it requires two low pass filters; one for the real branch and one for the imaginary branch. A more efficient way is to transform the real signal to a complex signal and then complex heterodyne the resultant signal to baseband. The transformation of a real signal to a complex signal can be done using a Hilbert transform. Building a Hilbert transform directly from its sampled data sequence produces suboptimal results due to time series truncation; another method is building a Hilbert transformer by synthesizing the filter coefficients from half Figure 1: A quadrature down-converter band filter coefficients. Designing the Hilbert transform filter using a half band filter allows for a much more Another way of viewing the problem is that the structured design process as well as greatly improved quadrature down-converter not only extracts the desired results. segment of the spectrum it rejects the undesired spectral image, the spectral replica present in the Hermetian 1. INTRODUCTION symmetric spectra of a real signal. Removing this image would result in a single sided spectrum which being non- The digital portion of a receiver is typically designed to Hermetian symmetric is the transform of a complex signal.
    [Show full text]
  • A Pulse Compression Waveform for Improved-Sensitivity Weather Radar Observations
    DECEMBER 2014 K U R D Z O E T A L . 2713 A Pulse Compression Waveform for Improved-Sensitivity Weather Radar Observations JAMES M. KURDZO School of Meteorology, and Advanced Radar Research Center, University of Oklahoma, Norman, Oklahoma BOON LENG CHEONG Advanced Radar Research Center, University of Oklahoma, Norman, Oklahoma ROBERT D. PALMER AND GUIFU ZHANG School of Meteorology, and Advanced Radar Research Center, University of Oklahoma, Norman, Oklahoma JOHN B. MEIER Advanced Radar Research Center, University of Oklahoma, Norman, Oklahoma (Manuscript received 22 January 2013, in final form 9 September 2014) ABSTRACT The progression of phased array weather observations, research, and planning over the past decade has led to significant advances in development efforts for future weather radar technologies. However, numerous challenges still remain for large-scale deployment. The eventual goal for phased array weather radar tech- nology includes the use of active arrays, where each element would have its own transmit/receive module. This would lead to significant advantages; however, such a design must be capable of utilizing low-power, solid-state transmitters at each element in order to keep costs down. To provide acceptable sensitivity, as well as the range resolution needed for weather observations, pulse compression strategies are required. Pulse compression has been used for decades in military applications, but it has yet to be applied on a broad scale to weather radar, partly because of concerns regarding sensitivity loss caused by pulse windowing. A robust optimization technique for pulse compression waveforms with minimalistic windowing using a genetic al- gorithm is presented. A continuous nonlinear frequency-modulated waveform that takes into account transmitter distortion is shown, both in theory and in practical use scenarios.
    [Show full text]
  • An FPGA-BASED Implementation of a Hilbert Filter for Real-Time Estimation of Instantaneous Frequency, Phase and Amplitude of Power System Signals
    International Journal of Applied Engineering Research ISSN 0973-4562 Volume 13, Number 23 (2018) pp. 16333-16341 © Research India Publications. http://www.ripublication.com An FPGA-BASED implementation of a Hilbert filter for Real-time Estimation of Instantaneous Frequency, Phase and Amplitude of Power System Signals Q. Bart and R. Tzoneva Department of Electrical, Electronic and Computer Engineering, Cape Peninsula University of Technology, Cape town, 7535, South Africa. Abstract apriori knowledge for a particular fixed sampling rate. The DFT is periodic in nature and assumes that the window of The instantaneous parameters, amplitude, phase and sampled data contains an integer number of waveform cycles. frequency of power system signals provide valuable During frequency perturbations the sampled data may not information about the status of the power system, particularly comprise an integer number of cycles resulting in when these parameters can be obtained simultaneously from discontinuities at the endpoints. This is one of the locations that are remotely located from each other. Phasor disadvantages of the DFT for real-time estimation of Measurement Units (PMU’s) placed at these remote locations synchrophasors and this phenomenon is commonly known as can perform these simultaneous time synchronized spectral leakage. In order to accommodate the dynamic measurements. In this work digital signal processing nature of power system signals an extension of the DFT techniques and Field Programmable Gate Array (FPGA) known as the Taylor-Fourier Transform [4],[5] has also been technology was used for the real-time estimation of power utilized as a synchrophasor estimator. Alternative techniques system signal parameters. These parameters were estimated such as Kalman Filtering [6] and Enhanced Phase Locked based upon an approach utilizing the Hilbert transform and Loop techniques [7] have also been proposed.
    [Show full text]
  • Arxiv:1611.05269V3 [Cs.IT] 29 Jan 2018 Graph Analytic Signal, and Associated Amplitude and Frequency Modulations Reveal Com
    On Hilbert Transform, Analytic Signal, and Modulation Analysis for Signals over Graphs Arun Venkitaraman, Saikat Chatterjee, Peter Handel¨ Department of Information Science and Engineering, School of Electrical Engineering and ACCESS Linnaeus Center KTH Royal Institute of Technology, SE-100 44 Stockholm, Sweden . Abstract We propose Hilbert transform and analytic signal construction for signals over graphs. This is motivated by the popularity of Hilbert transform, analytic signal, and mod- ulation analysis in conventional signal processing, and the observation that comple- mentary insight is often obtained by viewing conventional signals in the graph setting. Our definitions of Hilbert transform and analytic signal use a conjugate-symmetry-like property exhibited by the graph Fourier transform (GFT), resulting in a ’one-sided’ spectrum for the graph analytic signal. The resulting graph Hilbert transform is shown to possess many interesting mathematical properties and also exhibit the ability to high- light anomalies/discontinuities in the graph signal and the nodes across which signal discontinuities occur. Using the graph analytic signal, we further define amplitude, phase, and frequency modulations for a graph signal. We illustrate the proposed con- cepts by showing applications to synthesized and real-world signals. For example, we show that the graph Hilbert transform can indicate presence of anomalies and that arXiv:1611.05269v3 [cs.IT] 29 Jan 2018 graph analytic signal, and associated amplitude and frequency modulations reveal com- plementary information in speech signals. Keywords: Graph signal, analytic signal, Hilbert transform, demodulation, anomaly detection. Email addresses: [email protected] (Arun Venkitaraman), [email protected] (Saikat Chatterjee), [email protected] (Peter Handel)¨ Preprint submitted to Signal Processing 1 1 0.8 0.8 0.6 0.6 0.4 0.4 0.2 0.2 0 0 (a) (b) Figure 1: Anomaly highlighting behavior of the graph Hilbert transform for 2D image signal graph.
    [Show full text]
  • New Non-Linear FM Pulse-Compression Technique for Radar Applications
    University of Central Florida STARS Retrospective Theses and Dissertations 1985 New Non-Linear FM Pulse-Compression Technique for Radar Applications Ronald A. Booher University of Central Florida Part of the Engineering Commons Find similar works at: https://stars.library.ucf.edu/rtd University of Central Florida Libraries http://library.ucf.edu This Masters Thesis (Open Access) is brought to you for free and open access by STARS. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of STARS. For more information, please contact [email protected]. STARS Citation Booher, Ronald A., "New Non-Linear FM Pulse-Compression Technique for Radar Applications" (1985). Retrospective Theses and Dissertations. 4806. https://stars.library.ucf.edu/rtd/4806 NEW NON-LINEAR FM PULSE-COMPRESSION TECHNIQUE FOR RADAR APPLICATIONS BY RONALD A. BOOHER B.S.E., University of Central Florida, 1984 THESIS Submitted in partial fulfillment of the requirements for the degree of Master of Science .in Engineering in the Graduate Studies Program of the College of Engineering University of Central Florida Orlando, Florida Fall Tenn 1985 ABSTRACT The development of pulsed type radar signals is examined, with a brief review of matched filtering. Gated RF, linear and non-linear FM pulse-compression ~hirp) and matched filtering of radar signals is reviewed in depth. Emphasis is given to identifying the desirable characteristics of each method. A new method of non-linear FM pulse-compression is introduced; it utilizes the Eigen Function (a form of the raised-cosine family) of functions) as its modulating term. Its properties are then compared to those of the linear and non-linear systems reviewed in the preceding sections.
    [Show full text]
  • Complex Exponentials and Spectrum Representation
    Music 270a: Complex Exponentials and Spectrum Representation Tamara Smyth, [email protected] Department of Music, University of California, San Diego (UCSD) October 21, 2019 1 Exponentials The exponential function is typically used to describe • the natural growth or decay of a system’s state. An exponential function is defined as • t/τ x(t)= e− , where e =2.7182..., and τ is the characteristic time constant, the time it takes to decay by 1/e. τ Exponential, e−t/ 1 0.9 0.8 0.7 0.6 0.5 0.4 1/e 0.3 0.2 0.1 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 Time (s) Figure 1: Exponentials with characteristic time constants, .1, .2, .3, .4, and .5 Both exponential and sinusoidal functions are aspects • of a slightly more complicated function. Music 270a: Complex Exponentials and Spectrum Representation 2 Complex numbers Complex numbers provides a system for • 1. manipulating rotating vectors, and 2. representing geometric effects of common digital signal processing operations (e.g. filtering), in algebraic form. In rectangular (or Cartesian) form, the complex • number z is defined by the notation z = x + jy. The part without the j is called the real part, and • the part with the j is called the imaginary part. Music 270a: Complex Exponentials and Spectrum Representation 3 Complex Numbers as Vectors A complex number can be drawn as a vector, the tip • of which is at the point (x, y), where x , the horizontal coordinate—the real part, y , the vertical coordinate—the imaginary part.
    [Show full text]
  • Applications of Analytic Function Theory to Analysis of Single-Sideband Angle-Modulated Systems
    TECHNICAL NASA NOTE NASA TNA D-5446 =-­ e. z c 4 c/I 4 z LOAN COPY: RETURN TC.) AFWL (WWL-2) KIRTLAND AFB, N MEX APPLICATIONS OF ANALYTIC FUNCTION THEORY TO ANALYSIS OF SINGLE-SIDEBAND ANGLE-MODULATED SYSTEMS by John H. Painter r Langley Research Center i ! Langley Station, Hdmpton, Vd. &iii I NATIONAL AERONAUTICS AND SPACE ADMINISTRATION WASHINGTON, D. C. SEPTEMBER 1969 71 d TECH LIBRARY KAFB, "I \lllllllllll. .. I1111 Illlllllllllllllllllllll 01320b2 1. Report No. 2. Government Accession No. 3. Recipient's Catalog No. NASA TN D-5446 I 4. Title and Subtitle 5. Report Date September 1969 APPLICATIONS OF ANALYTIC FUNCTION THEORY TO ANALYSIS 6. Performing Organization Co OF SINGLE-SIDEBAND ANGLE-MODULATED SYSTEMS 7. Author(s) 8. Performing Orgonization Re John H. Painter L-6562 9. Performing Orgonization Name and Address 0. Work Unit No. 125-21-05-01-23 NASA Langley Research Center Hampton, Va. 23365 1. Contract or Grant No. 3. Type of Report and Period 2. Sponsoring Agency Name ond Address Technical Note National Aeronautics and Space Administration Washington, D.C. 20546 4. Sponsoring Agency Code 15. Supplementary Notes 16. Abstract This paper applies the theory and notation of complex analytic ti" unctions and stochastic process6 to the investigation of the single-sideband angle-modulation process. Low-deviation modulation and linear product detection in the presence of noise are carefully examined for the case of sinusoidal modulation. Modulation by an arbitrary number of sinusoids or by modulated subcarriers is considered. Also treated is a method for increasing modulation efficiency. The paper concludes with an examination of the asymp­ totic (low-noise) performance of nonlinear detection of a single-sideband carrier which is heavily frequenc modulated by a Gaussian process.
    [Show full text]
  • Matched-Filter Ultrasonic Sensing: Theory and Implementation Zhaohong Zhang
    White Paper SLAA814–December 2017 Matched-Filter Ultrasonic Sensing: Theory and Implementation Zhaohong Zhang ........................................................................................................... MSP Systems This document provides a detailed discussion on the operating theory of the matched-filter based ultrasonic sensing technology and the single-chip implementation platform using the Texas Instruments (TI) MSP430FR6047 microcontroller (MCU). Contents 1 Introduction ................................................................................................................... 2 2 Theory of Matched Filtering ................................................................................................ 2 3 MSP430FR6047 for Ultrasonic Sensing .................................................................................. 5 4 MSP430FR6047 USS Subsystem......................................................................................... 6 5 MSP430FR6047 Low Energy Accelerator (LEA) ........................................................................ 8 6 References ................................................................................................................... 9 List of Figures 1 Sonar in Target Range Measurement .................................................................................... 2 2 Concept of Pulse Compression............................................................................................ 2 3 Time-Domain Waveform and Autocorrelation of FM Chirp............................................................
    [Show full text]
  • PART0001 (Pulse Compression for Phased Array Weather Radars.)
    NCAR/TN-444 NCAR TECHNICAL NOTE _· i May 1999 Pulse Compression for Phased Array Weather Radars R. Jeffrey Keeler Charles A. Hwang Ashok S. Mudukutore ATMOSPHERIC TECHNOLOGY DIVISION i NATIONAL CENTER FOR ATMOSPHERIC RESEARCH BOULDER, COLORADO - Pulse Compression for Phased Array Weather Radars NCAR Technical Report I R. Jeffrey Keeler 1, Charles A. Hwang1 and Ashok Mudukutore 2 1National Center for Atmospheric Research* PO Box 3000, Boulder, Colorado 80307 USA 2Colorado State University Fort Collins, Colorado 80369 USA E-mail: keeler@ucaredu Tel: 303-497-2031 Fax: 303-497-2044 *NCAR is operated by the University Corporation for Atmospheric Research under sponsorship of the National Science Foundation Preface This Technical Report is a reprint of the Final Report from NCAR's Atmospheric Technology Division on work per- formed from 1991 through 1995 for the FAA Terminal Area Surveillance Systems Program. It details the application of pulse compression waveforms to weather radar, the importance of range time sidelobes, special considerations for FM waveforms, simulations of fluctuating weather targets, and a validation study using the NCAR ELDORA testbed radar. The report was originally written in 1995, but not published until now. A few relevant references have been added when they amplify the work originally performed. rJK May 15, 1999 List of figures Figure 1.1. Advanced high resolution radarsystem using pulse compression waveform and phased array electronic scanned antenna . ..................................................... ................................................. .................................................. 2 Figure 2.1. Graphicaldescription of optimal sidelobe suppressionfilter design. The desiredoutput response, dk, is an impulse, but the actual output, yk, has sidelobes. ........ 6.................................................................................................6 Figure 2.2. The integratedsidelobe levels (ISL)for a Barker 13 code with inversefiltering decrease with longerfilter length for zero Doppler.
    [Show full text]