DOCSLIB.ORG

Instantaneous Frequency and Amplitude of Complex Signals Based on Quaternion Fourier Transform

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Instantaneous Frequency and Amplitude of Complex Signals Based on Quaternion Fourier Transform Instantaneous frequency and amplitude of complex signals based on quaternion Fourier transform Nicolas Le Bihan∗ Stephen J. Sangwiney Todd A. Ellz August 8, 2012 Abstract plex modulation can be represented mathematically by a polar representation of quaternions previously The ideas of instantaneous amplitude and phase are derived by the authors. As in the classical case, there well understood for signals with real-valued samples, is a restriction of non-overlapping frequency content based on the analytic signal which is a complex sig- between the modulating complex signal and the or- nal with one-sided Fourier transform. We extend thonormal complex exponential. We show that, un- these ideas to signals with complex-valued samples, der these conditions, modulation in the time domain using a quaternion-valued equivalent of the analytic is equivalent to a frequency shift in the quaternion signal obtained from a one-sided quaternion Fourier Fourier domain. Examples are presented to demon- transform which we refer to as the hypercomplex rep- strate these concepts. resentation of the complex signal. We present the necessary properties of the quaternion Fourier trans- form, particularly its symmetries in the frequency do- 1 Introduction main and formulae for convolution and the quater- nion Fourier transform of the Hilbert transform. The The instantaneous amplitude and phase of a real- hypercomplex representation may be interpreted as valued signal have been understood since 1948 from an ordered pair of complex signals or as a quater- the work of Ville [1] and Gabor [2] based on the nion signal. We discuss its derivation and proper- analytic signal. A critical discussion of instanta- ties and show that its quaternion Fourier transform neous amplitude and phase was given by Picinbono is one-sided. It is shown how to derive from the hy- in 1997, particularly with reference to amplitude and percomplex representation a complex envelope and a phase modulation [3, V]. The analytic signal and x phase. its associated modulation concepts can be simply de- A classical result in the case of real signals is that scribed, even though a full theoretical treatment is an amplitude modulated signal may be analysed into quite deep. Given a real-valued signal f(t), the cor- its envelope and carrier using the analytic signal pro- responding analytic signal a(t) is a complex signal vided that the modulating signal has frequency con- with real part equal to f(t) and imaginary part or- tent not overlapping with that of the carrier. We thogonal to f(t). The imaginary part is sometimes show that this idea extends to the complex case, known as the quadrature signal { in the case where arXiv:1208.1363v1 [math.NA] 7 Aug 2012 provided that the complex signal modulates an or- f(t) is a sinusoid, the imaginary part of the analytic thonormal complex exponential. Orthonormal com- signal is in quadrature, that is with a phase differ- ence of π=2. The orthogonal signal is related to f(t) − ∗Nicolas Le Bihan is with the CNRS, GIPSA-Lab, by the Hilbert transform [4, 5]. The analytic signal D´epartement Images et Signal, 961 Rue de la Houille Blanche, has the interesting property that its modulus a(t) is Domaine Universitaire, BP 46, 38402 Saint Martin d'H`eres j j cedex, France, email: [email protected] an envelope of the signal f(t). The envelope is also inp.fr known as the instantaneous amplitude. Thus if f(t) is yStephen J. Sangwine is with the School of Computer Sci- an amplitude-modulated sinusoid, the envelope a(t) , ence and Electronic Engineering, University of Essex, Colch- subject to certain conditions on the frequencyj con-j ester, CO4 3SQ, United Kingdom, email: [email protected] tent, is the modulating signal. The argument of the zTodd A. Ell is with Goodrich Sensors & Integrated Sys- tems, 14300 Judicial Road, Burnsville, MN 55306 USA, email: analytic signal, \ a(t) is known as the instantaneous [email protected] phase and its derivative is known as the instanta- 1 neous frequency. The analytic signal has a further a complex signal, for reasons which should be evi- very interesting property: it has a one-sided Fourier dent later in the paper. Note that, in essence, the transform. Thus a simple method for constructing approach proposed in this paper is inspired by the the analytic signal (algebraically or numerically) is work of B¨ulow [8, 9] and Labunets [10] who consid- to compute the Fourier transform of f(t), multiply ered Clifford Fourier transforms (quaternion in the the Fourier transform by a unit step which is zero for case of B¨ulow) to process multidimensional signals. negative frequencies, and then construct the inverse While B¨ulow considered 2D signals (images), here we Fourier transform of the resulting spectrum. consider 1D signals with 2D samples (complex val- ued samples). We are not focusing on any particular In this paper we extend the above ideas to sig- application in this paper, rather we propose a new nals with complex-valued samples. We show that approach to the processing of complex valued signals if a quaternion Fourier transform is computed from (including proper and improper signals, even though a complex-valued signal, and negative frequencies in proper signals are well-described using the classical the frequency domain representation are suppressed, complex Fourier transform | they are a special case.) the inverse quaternion Fourier transform gives an Schreier and Scharf's book gives examples of appli- equivalent of the analytic signal, which we refer to cations [6]. in this paper as a hypercomplex representation of the complex signal. Just as the classical analytic signal The idea of amplitude modulation is extended to represents a real-valued signal by a complex signal the case where the modulating signal is complex, and (that is with a pair of real signals), the hypercomplex the `carrier' is an orthonormal complex exponential, representation presented here represents a complex- that is a complex exponential which is in a com- valued signal by a quaternion signal (that is with a plex plane orthogonal to the complex plane of the pair of complex signals, based on the Cayley-Dickson modulating signal { this concept is easily realised form of a quaternion). using quaternions, since quaternion algebra has a 4-dimensional basis with three mutually orthogonal We consider signals with complex-valued samples imaginary units. Subject to the same restrictions on in a most general sense, without any restrictions frequency content as in the real-valued case, ampli- on the relationship between the real and imaginary tude modulation in the time domain corresponds to parts. However, we exclude the special case of an a frequency shift in the Fourier domain. Further, a analytic signal (where the real and imaginary parts complex envelope of the hypercomplex representation are orthogonal) because it does not possess an in- can be defined which recovers the complex modulat- teresting hypercomplex representation: the two ad- ing signal. This is the complex instantaneous ampli- ditional quaternion components of the hypercomplex tude. Further, the phase of the orthonormal complex representation are simply copies of the two original exponential may be recovered. This is the instanta- components. The case where the real and imaginary neous phase, and its derivative is the instantaneous parts are correlated in some statistical sense is called frequency. In the case of modulation of a complex ex- improper, whereas an analytic signal is proper. It has ponential the instantaneous frequency is that of the been customary to handle such signals by using an complex exponential `carrier'. Just as the classical augmented representation consisting of a vector con- complex analytic signal contains both the original taining the signal and its conjugate [6]. Recently, real signal (in the real part) and a real orthogonal Lilly and Olhede [7] have published a paper on bi- signal (in the imaginary part), our hypercomplex sig- variate analytic signal concepts. Their approach is nal representation contains two complex signals: the linked to a specific signal model, the modulated ellip- original signal and an orthogonal signal. tical signal, which they illustrate with the example of a drifting oceanographic float, and they utilise pairs We have previously published partial results on of analytic signals derived from the pair of real signals this topic [11{13] as we developed the ideas presented representing the time-varying positional coordinates here. The idea of orthonormal complex modulation of a drifting float. In this paper a different approach, has not previously been presented. using hypercomplex representation, is considered be- The sequence of topics in the rest of the paper is cause it is more suited to the analysis of modulation, as follows. Section 2 presents the quaternion algebra and also because we have at our disposal the existing and quaternion Fourier transform concepts used to tools of quaternion Fourier transforms, which provide construct the hypercomplex representation of a com- a natural fit with modulation of a complex signal by plex signal using a one-sided quaternion spectrum. 2 i Section 3 discusses the hypercomplex representation z1 + z2j in the basis 1; i; j; k with z1; z2 C , i.e. f g 2 of a complex signal. Section 4 discusses the instanta- zα = (zα) + i (zα) for α = 1; 2. This is called the neous amplitude and frequency concept for a complex Cayley-Dickson< = form of q. signal through its hypercomplex representation. Sec- Among the possible representations of q, we will tion 5 presents some signal examples to illustrate the make use in this paper of one that was recently in- ideas presented in the paper. troduced: the polar Cayley-Dickson form [16]. Any quaternion q also has a unique polar Cayley-Dickson 2 Quaternion Fourier form given by: Transform q = Aq exp(Bqj) = (a0 + a1i) exp((b0 + b1i)j) (3) where Aq = a0 + a1i is the complex modulus of q and In this section, we present the definition and prop- Bq = b0 +b1i its complex phase.
Load more

Recommended publications
  • Optical Single Sideband for Broadband and Subcarrier Systems
    University of Alberta Optical Single Sideband for Broadband And Subcarrier Systems Robert James Davies 0 A thesis submitted to the faculty of Graduate Studies and Research in partial fulfillrnent of the requirernents for the degree of Doctor of Philosophy Department of Electrical And Computer Engineering Edmonton, AIberta Spring 1999 National Library Bibliothèque nationale du Canada Acquisitions and Acquisitions et Bibliographie Services services bibliographiques 395 Wellington Street 395, rue Wellington Ottawa ON KlA ON4 Ottawa ON KIA ON4 Canada Canada Yom iUe Votre relérence Our iSie Norre reference The author has granted a non- L'auteur a accordé une licence non exclusive licence allowing the exclusive permettant à la National Library of Canada to Bibliothèque nationale du Canada de reproduce, loan, distribute or sell reproduire, prêter, distribuer ou copies of this thesis in microform, vendre des copies de cette thèse sous paper or electronic formats. la forme de microfiche/nlm, de reproduction sur papier ou sur format électronique. The author retains ownership of the L'auteur conserve la propriété du copyright in this thesis. Neither the droit d'auteur qui protège cette thèse. thesis nor substantial extracts fkom it Ni la thèse ni des extraits substantiels may be printed or otheMrise de celle-ci ne doivent être Unprimés reproduced without the author's ou autrement reproduits sans son permission. autorisation. Abstract Radio systems are being deployed for broadband residential telecommunication services such as broadcast, wideband lntemet and video on demand. Justification for radio delivery centers on mitigation of problems inherent in subscriber loop upgrades such as Fiber to the Home (WH)and Hybrid Fiber Coax (HFC).
    [Show full text]
  • 3 Characterization of Communication Signals and Systems
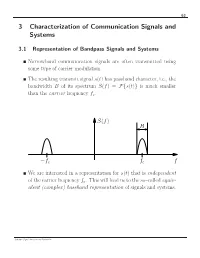
    63 3 Characterization of Communication Signals and Systems 3.1 Representation of Bandpass Signals and Systems Narrowband communication signals are often transmitted using some type of carrier modulation. The resulting transmit signal s(t) has passband character, i.e., the bandwidth B of its spectrum S(f) = s(t) is much smaller F{ } than the carrier frequency fc. S(f) B f f f − c c We are interested in a representation for s(t) that is independent of the carrier frequency fc. This will lead us to the so–called equiv- alent (complex) baseband representation of signals and systems. Schober: Signal Detection and Estimation 64 3.1.1 Equivalent Complex Baseband Representation of Band- pass Signals Given: Real–valued bandpass signal s(t) with spectrum S(f) = s(t) F{ } Analytic Signal s+(t) In our quest to find the equivalent baseband representation of s(t), we first suppress all negative frequencies in S(f), since S(f) = S( f) is valid. − The spectrum S+(f) of the resulting so–called analytic signal s+(t) is defined as S (f) = s (t) =2 u(f)S(f), + F{ + } where u(f) is the unit step function 0, f < 0 u(f) = 1/2, f =0 . 1, f > 0 u(f) 1 1/2 f Schober: Signal Detection and Estimation 65 The analytic signal can be expressed as 1 s+(t) = − S+(f) F 1{ } = − 2 u(f)S(f) F 1{ } 1 = − 2 u(f) − S(f) F { } ∗ F { } 1 The inverse Fourier transform of − 2 u(f) is given by F { } 1 j − 2 u(f) = δ(t) + .
    [Show full text]
  • Design and Application of a Hilbert Transformer in a Digital Receiver
    Proceedings of the SDR 11 Technical Conference and Product Exposition, Copyright © 2011 Wireless Innovation Forum All Rights Reserved DESIGN AND APPLICATION OF A HILBERT TRANSFORMER IN A DIGITAL RECEIVER Matt Carrick (Northrop Grumman, Chantilly, VA, USA; [email protected]); Doug Jaeger (Northrop Grumman, Chantilly, VA, USA; [email protected]); fred harris (San Diego State University, San Diego, CA, USA; [email protected]) ABSTRACT A common method of down converting a signal from an intermediate frequency (IF) to baseband is using a quadrature down-converter. One problem with the quadrature down-converter is it requires two low pass filters; one for the real branch and one for the imaginary branch. A more efficient way is to transform the real signal to a complex signal and then complex heterodyne the resultant signal to baseband. The transformation of a real signal to a complex signal can be done using a Hilbert transform. Building a Hilbert transform directly from its sampled data sequence produces suboptimal results due to time series truncation; another method is building a Hilbert transformer by synthesizing the filter coefficients from half Figure 1: A quadrature down-converter band filter coefficients. Designing the Hilbert transform filter using a half band filter allows for a much more Another way of viewing the problem is that the structured design process as well as greatly improved quadrature down-converter not only extracts the desired results. segment of the spectrum it rejects the undesired spectral image, the spectral replica present in the Hermetian 1. INTRODUCTION symmetric spectra of a real signal. Removing this image would result in a single sided spectrum which being non- The digital portion of a receiver is typically designed to Hermetian symmetric is the transform of a complex signal.
    [Show full text]
  • An FPGA-BASED Implementation of a Hilbert Filter for Real-Time Estimation of Instantaneous Frequency, Phase and Amplitude of Power System Signals
    International Journal of Applied Engineering Research ISSN 0973-4562 Volume 13, Number 23 (2018) pp. 16333-16341 © Research India Publications. http://www.ripublication.com An FPGA-BASED implementation of a Hilbert filter for Real-time Estimation of Instantaneous Frequency, Phase and Amplitude of Power System Signals Q. Bart and R. Tzoneva Department of Electrical, Electronic and Computer Engineering, Cape Peninsula University of Technology, Cape town, 7535, South Africa. Abstract apriori knowledge for a particular fixed sampling rate. The DFT is periodic in nature and assumes that the window of The instantaneous parameters, amplitude, phase and sampled data contains an integer number of waveform cycles. frequency of power system signals provide valuable During frequency perturbations the sampled data may not information about the status of the power system, particularly comprise an integer number of cycles resulting in when these parameters can be obtained simultaneously from discontinuities at the endpoints. This is one of the locations that are remotely located from each other. Phasor disadvantages of the DFT for real-time estimation of Measurement Units (PMU’s) placed at these remote locations synchrophasors and this phenomenon is commonly known as can perform these simultaneous time synchronized spectral leakage. In order to accommodate the dynamic measurements. In this work digital signal processing nature of power system signals an extension of the DFT techniques and Field Programmable Gate Array (FPGA) known as the Taylor-Fourier Transform [4],[5] has also been technology was used for the real-time estimation of power utilized as a synchrophasor estimator. Alternative techniques system signal parameters. These parameters were estimated such as Kalman Filtering [6] and Enhanced Phase Locked based upon an approach utilizing the Hilbert transform and Loop techniques [7] have also been proposed.
    [Show full text]
  • Arxiv:1611.05269V3 [Cs.IT] 29 Jan 2018 Graph Analytic Signal, and Associated Amplitude and Frequency Modulations Reveal Com
    On Hilbert Transform, Analytic Signal, and Modulation Analysis for Signals over Graphs Arun Venkitaraman, Saikat Chatterjee, Peter Handel¨ Department of Information Science and Engineering, School of Electrical Engineering and ACCESS Linnaeus Center KTH Royal Institute of Technology, SE-100 44 Stockholm, Sweden . Abstract We propose Hilbert transform and analytic signal construction for signals over graphs. This is motivated by the popularity of Hilbert transform, analytic signal, and mod- ulation analysis in conventional signal processing, and the observation that comple- mentary insight is often obtained by viewing conventional signals in the graph setting. Our definitions of Hilbert transform and analytic signal use a conjugate-symmetry-like property exhibited by the graph Fourier transform (GFT), resulting in a ’one-sided’ spectrum for the graph analytic signal. The resulting graph Hilbert transform is shown to possess many interesting mathematical properties and also exhibit the ability to high- light anomalies/discontinuities in the graph signal and the nodes across which signal discontinuities occur. Using the graph analytic signal, we further define amplitude, phase, and frequency modulations for a graph signal. We illustrate the proposed con- cepts by showing applications to synthesized and real-world signals. For example, we show that the graph Hilbert transform can indicate presence of anomalies and that arXiv:1611.05269v3 [cs.IT] 29 Jan 2018 graph analytic signal, and associated amplitude and frequency modulations reveal com- plementary information in speech signals. Keywords: Graph signal, analytic signal, Hilbert transform, demodulation, anomaly detection. Email addresses: [email protected] (Arun Venkitaraman), [email protected] (Saikat Chatterjee), [email protected] (Peter Handel)¨ Preprint submitted to Signal Processing 1 1 0.8 0.8 0.6 0.6 0.4 0.4 0.2 0.2 0 0 (a) (b) Figure 1: Anomaly highlighting behavior of the graph Hilbert transform for 2D image signal graph.
    [Show full text]
  • Complex Exponentials and Spectrum Representation
    Music 270a: Complex Exponentials and Spectrum Representation Tamara Smyth, [email protected] Department of Music, University of California, San Diego (UCSD) October 21, 2019 1 Exponentials The exponential function is typically used to describe • the natural growth or decay of a system’s state. An exponential function is defined as • t/τ x(t)= e− , where e =2.7182..., and τ is the characteristic time constant, the time it takes to decay by 1/e. τ Exponential, e−t/ 1 0.9 0.8 0.7 0.6 0.5 0.4 1/e 0.3 0.2 0.1 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 Time (s) Figure 1: Exponentials with characteristic time constants, .1, .2, .3, .4, and .5 Both exponential and sinusoidal functions are aspects • of a slightly more complicated function. Music 270a: Complex Exponentials and Spectrum Representation 2 Complex numbers Complex numbers provides a system for • 1. manipulating rotating vectors, and 2. representing geometric effects of common digital signal processing operations (e.g. filtering), in algebraic form. In rectangular (or Cartesian) form, the complex • number z is defined by the notation z = x + jy. The part without the j is called the real part, and • the part with the j is called the imaginary part. Music 270a: Complex Exponentials and Spectrum Representation 3 Complex Numbers as Vectors A complex number can be drawn as a vector, the tip • of which is at the point (x, y), where x , the horizontal coordinate—the real part, y , the vertical coordinate—the imaginary part.
    [Show full text]
  • Applications of Analytic Function Theory to Analysis of Single-Sideband Angle-Modulated Systems
    TECHNICAL NASA NOTE NASA TNA D-5446 =-­ e. z c 4 c/I 4 z LOAN COPY: RETURN TC.) AFWL (WWL-2) KIRTLAND AFB, N MEX APPLICATIONS OF ANALYTIC FUNCTION THEORY TO ANALYSIS OF SINGLE-SIDEBAND ANGLE-MODULATED SYSTEMS by John H. Painter r Langley Research Center i ! Langley Station, Hdmpton, Vd. &iii I NATIONAL AERONAUTICS AND SPACE ADMINISTRATION WASHINGTON, D. C. SEPTEMBER 1969 71 d TECH LIBRARY KAFB, "I \lllllllllll. .. I1111 Illlllllllllllllllllllll 01320b2 1. Report No. 2. Government Accession No. 3. Recipient's Catalog No. NASA TN D-5446 I 4. Title and Subtitle 5. Report Date September 1969 APPLICATIONS OF ANALYTIC FUNCTION THEORY TO ANALYSIS 6. Performing Organization Co OF SINGLE-SIDEBAND ANGLE-MODULATED SYSTEMS 7. Author(s) 8. Performing Orgonization Re John H. Painter L-6562 9. Performing Orgonization Name and Address 0. Work Unit No. 125-21-05-01-23 NASA Langley Research Center Hampton, Va. 23365 1. Contract or Grant No. 3. Type of Report and Period 2. Sponsoring Agency Name ond Address Technical Note National Aeronautics and Space Administration Washington, D.C. 20546 4. Sponsoring Agency Code 15. Supplementary Notes 16. Abstract This paper applies the theory and notation of complex analytic ti" unctions and stochastic process6 to the investigation of the single-sideband angle-modulation process. Low-deviation modulation and linear product detection in the presence of noise are carefully examined for the case of sinusoidal modulation. Modulation by an arbitrary number of sinusoids or by modulated subcarriers is considered. Also treated is a method for increasing modulation efficiency. The paper concludes with an examination of the asymp­ totic (low-noise) performance of nonlinear detection of a single-sideband carrier which is heavily frequenc modulated by a Gaussian process.
    [Show full text]
  • Bandpass Filters and Hilbert Transform
    Bandpass filters and Hilbert Transform Summary of Chapter 14 In Analyzing Neural Time Series Data: Theory and Practice Lauritz W. Dieckman A quick message from Mike X I've created a googlegroups for the book. If you have other questions about the book, analyses, or code, feel free to post them there. https://groups.google.com/forum/#!forum/a nalyzingneuraltimeseriesdata Filters ‐Everywhere • Music ‐analog recordings ~44,100 Hz sampling ‐typically bandpass filtered to range of human hearing ‐Or, purposefully Used in artistic creation ‐One persons distortion is another persons art Why? Filter‐Hilbert Method vs Complex Wavelet Convolution Similarities • Used to create a complex (real and imaginary) time series (analytic signal) from real signal data • Analytic signal used to determine phase and power ‐Methods described in Chapter 13 • The signal must be bandpass filtered before Why? Filter‐Hilbert Method vs Complex Wavelet Convolution Differences • Signal must first be bandpass filtered • Analytic signal acquired by creating the “phase quadrature component” (one quarter‐cycle) by rotating sections of a Fourier spectrum. • PRO: Filter‐Hilbert provides superior control over frequency filtering ‐not limited in shape whereas bandpass filters can take many shapes • CON: However, Filter‐Hilbert requires signal processing toolbox for kernel creation (unlike Morlet wavelets). • CON: Bandpass filtering is slower than wavelets Bandpass Filtering • First step is Bandpass filtering ‐Don’t worry Hilbert fans, we’ll get back to Hilbert transform soon • Highly recommended to separate frequencies before the transform ‐e.g. lower frequencies may dominate combined signal Filters: To Infinity and… much shorter • Finite Impulse Response (FIR) SOON I will reign –The responsesupreme to an and impulse ends at some point.infinite over your ‐Stability analytic signal ‐Computation time ‐ Risk of phase distortions You will never triumph Infinite ImpulseButterworth.
    [Show full text]
  • Signal-Processing Framework for Ultrasound Compressed Sensing Data: Envelope Detection and Spectral Analysis
    applied sciences Article Signal-Processing Framework for Ultrasound Compressed Sensing Data: Envelope Detection and Spectral Analysis Yisak Kim, Juyoung Park and Hyungsuk Kim * Department of Electrical Engineering, Kwangwoon University, Seoul 139-701, Korea; [email protected] (Y.K.); [email protected] (J.P.) * Correspondence: [email protected] Received: 20 August 2020; Accepted: 30 September 2020; Published: 4 October 2020 Abstract: Acquisition times and storage requirements have become increasingly important in signal-processing applications, as the sizes of datasets have increased. Hence, compressed sensing (CS) has emerged as an alternative processing technique, as original signals can be reconstructed using fewer data samples collected at frequencies below the Nyquist sampling rate. However, further analysis of CS data in both time and frequency domains requires the reconstruction of the original form of the time-domain data, as traditional signal-processing techniques are designed for uncompressed data. In this paper, we propose a signal-processing framework that extracts spectral properties for frequency-domain analysis directly from under-sampled ultrasound CS data, using an appropriate basis matrix, and efficiently converts this into the envelope of a time-domain signal, avoiding full reconstruction. The technique generates more accurate results than the traditional framework in both time- and frequency-domain analyses, and is simpler and faster in execution than full reconstruction, without any loss of information. Hence, the proposed framework offers a new standard for signal processing using ultrasound CS data, especially for small and portable systems handling large datasets. Keywords: compressed sensing (CS); CS reconstruction; Fourier transform; envelope detection; Hilbert transform; analytic signal; ultrasound B-mode image; ultrasound attenuation map 1.
    [Show full text]
  • Easy Fourier Analysis
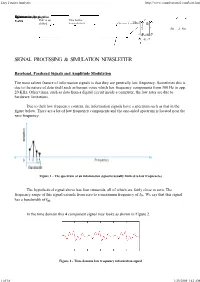
    Easy Fourier Analysis http://www.complextoreal.com/base.htm SpectrumDCInformationSignal term at 2w on csignal the positivenegative x-axis Half is up This half is shifted. down shifted. Charan Langton, The Carrier Editor fm = -1 fm = -9, fc-9,-9 -8, = -8, -8-7 -7 -9, -8, -7 SIGNAL PROCESSING & SIMULATION NEWSLETTER Baseband, Passband Signals and Amplitude Modulation The most salient feature of information signals is that they are generally low frequency. Sometimes this is due to the nature of data itself such as human voice which has frequency components from 300 Hz to app. 20 KHz. Other times, such as data from a digital circuit inside a computer, the low rates are due to hardware limitations. Due to their low frequency content, the information signals have a spectrum such as that in the figure below. There are a lot of low frequency components and the one-sided spectrum is located near the zero frequency. Figure 1 - The spectrum of an information signal is usually limited to low frequencies The hypothetical signal above has four sinusoids, all of which are fairly close to zero. The frequency range of this signal extends from zero to a maximum frequency of fm. We say that this signal has a bandwidth of fm. In the time domain this 4 component signal may looks as shown in Figure 2. Figure 2 - Time domain low frequency information signal 1 of 18 1/25/2008 3:42 AM Easy Fourier Analysis http://www.complextoreal.com/base.htm Now let’s modulate this signal, which means we are going to transfer it to a higher (usually much higher) frequency.
    [Show full text]
  • A New Discrete-Time Analytic Signal for Reducing Aliasing in Discrete Time–Frequency Distributions
    15th European Signal Processing Conference (EUSIPCO 2007), Poznan, Poland, September 3-7, 2007, copyright by EURASIP A NEW DISCRETE-TIME ANALYTIC SIGNAL FOR REDUCING ALIASING IN DISCRETE TIME–FREQUENCY DISTRIBUTIONS John M. O' Toole, Mostefa Mesbah and Boualem Boashash Perinatal Research Centre, University of Queensland, Royal Brisbane & Women's Hospital, Herston, QLD 4029, Australia. e-mail: [email protected] web: www.som.uq.edu.au/research/sprcg/ ABSTRACT tained from the finite discrete-time signal s(nT) of length N, The commonly used discrete-time analytic signal for discrete where T represents the sampling period. time–frequency distributions (DTFDs) contains spectral en- The requirements for an alias-free discrete-time, discrete- ergy at negative frequencies which results in aliasing in the frequency TFDs are as follows: a discrete-time TFD requires DTFD. A new discrete-time analytic signal is proposed that that a signal with half the Nyquist bandwidth is used, which approximately halves this spectral energy at the appropri- is the case for the analytic signal [2]. A discrete-frequency ate discrete negative frequencies. An empirical comparison TFD requires that a signal with half the time duration is shows that aliasing is reduced in the DTFD using the pro- used, that is s(nT) is zero for N < n ≤ 2N − 1 [3]. Thus posed analytic signal rather than the conventional analytic these two conditions must be combined to produce a discrete- signal. The time domain characteristics of the two analytic time, discrete-frequency TFD (simply referred to as a dis- signals are compared using an impulse signal as an exam- crete TFD, (DTFD)).
    [Show full text]
  • ADVANCED DSP ALGORITHMS in Telecommunication
    Applications of signal processors ADVANCED DSP ALGORITHMS in Telecommunication Author: Grzegorz Szwoch Gdańsk University of Technology, Department of Multimedia Systems Introduction Four algorithms selected from more advanced methods of digital signal processing, for practical application in telecommunication systems: ▪ signal resampling, decimation and interpolation; ▪ removal of changing distortion – adaptive filtering; ▪ frequency detection – autocorrelation; ▪ signal demodulation and envelope detection - analytic signal and Hilbert transformer. Signal resampling PROBLEM #1: sampling frequency 48 kHz is too low for our application. ▪ Oversampling – processing the signal with higher sampling frequency than the target one. ▪ In audio processing, signals are often oversampled 4-times, sampling frequency is 192 kHz. ▪ Drawback: more operations to perform; in signal oversampled by a factor of 4, DSP has to perform 4 times as much operations during the same time. Decimation ▪ At the output, we need a signal sampled with 48 kHz. ▪ If we have fs = 192 kHz, we have 4 times too much samples. ▪ Let’s take every 4th sample. Now, we have the number of samples we need. ▪ Before taking the samples, we need to process the oversampled signal with a low-pass decimation filter, with cut-off frequency equal to the target Nyquist frequency (24 kHz in our example). ▪ If we don’t apply the filter, aliasing occurs. Decimation Decimation from fs1 to fs2 = fs1 / D: ▪ low-pass filter with fc = fs2 / 2, ▪ then take every D-th sample. Example – generating a sawtooth wave f = 1 kHz: 4x oversampling with decimation No oversampling Interpolation ▪ We have a signal sampled with 48 kHz. How do we upsample it to 192 kHz? ▪ Let’s insert 3 zeros in between each pair of samples.
    [Show full text]