DOCSLIB.ORG

Mathematical Classification of Physical Quantities and Physics Relations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mathematical Classification of Physical Quantities and Physics Relations MATHEMATICAL CLASSIFICATION OF PHYSICAL QUANTITIES AND PHYSICS RELATIONS Thesis submitted to obtain the degree of Doctor of Philosophy Faculty of Sciences, Department of Mathematical physics and astronomy, University of Ghent, Belgium Philippe CHEVALIER Date: 13-11-2008 Version: draft 1 1 Table of contents 1 Table of contents ............................................................................................................................. 2 2 List of figures ................................................................................................................................... 6 3 Preface ............................................................................................................................................. 6 4 Introduction ..................................................................................................................................... 6 5 Definitions ....................................................................................................................................... 8 6 Base units in physics ........................................................................................................................ 8 6.1 Impact of the number of base units on physics .................................................................... 9 6.1.1 Description with one unit resulting in the graph 풗ퟎ풗ퟏ. ................................................. 9 6.1.2 Description with two units resulting in the graph 풗ퟎ풗ퟏ풗ퟐ ........................................... 9 6.1.3 Description with three units resulting in the graph 풗ퟎ풗ퟏ풗ퟐ풗ퟑ . .................................. 9 6.1.4 Description with four units resulting in the graph 풗ퟎ풗ퟏ풗ퟐ풗ퟑ풗ퟒ . ............................... 9 6.1.5 Description with five units resulting in the graph 풗ퟎ풗ퟏ풗ퟐ풗ퟑ풗ퟒ풗ퟓ.............................. 9 6.1.6 Description with six units resulting in the graph 풗ퟎ풗ퟏ풗ퟐ풗ퟑ풗ퟒ풗ퟓ풗ퟔ ........................ 10 6.1.7 Description with seven units resulting in the graph 풗ퟎ풗ퟏ풗ퟐ풗ퟑ풗ퟒ풗ퟓ풗ퟔ풗ퟕ .............. 10 6.1.8 Description with n units resulting in the graph 풗ퟎ풗ퟏ풗ퟐ풗ퟑ풗ퟒ풗ퟓ풗ퟔ … 풗퐧 ................. 10 7 Properties of 풁ퟕ for mathematical modelling of physics equations ............................................ 11 7.1 General mathematical properties and definitions applicable for 풁ퟕ ................................... 11 7.2 풁ퟕ integer lattice as representation of physical quantities .................................................. 11 7.3 Vector operations in 풁ퟕ ........................................................................................................ 12 7.3.1 Addition in 풁ퟕ ............................................................................................................... 12 7.3.2 Dot product in 풁ퟕ .......................................................................................................... 13 7.4 Map SUM() ............................................................................................................................ 15 7.5 Subgroups of 풁ퟕ for classification of physical quantities ..................................................... 16 7.6 Equivalence relation R as a classifier ..................................................................................... 17 7.7 Classification using Principal Component Analysis (PCA) ...................................................... 20 7.8 Classification using RPM mapping ......................................................................................... 33 7.9 Classification using Sammon map ......................................................................................... 37 7.10 Classification using Curvilinear Component Analysis ............................................................ 40 7.11 Graph of dimensionless products in 풁ퟕ ................................................................................ 43 7.12 Graph spectrum and graph eigenvalues ............................................................................... 52 7.13 Minimal spanning tree of a graph representing the physical quantity “force” in 풁ퟕ .......... 53 7.14 Syntax and semantics of “energy equations” ....................................................................... 56 2 7.14.1 Energy syntax N°2 .......................................................................................................... 57 7.14.2 Energy syntax N°3 .......................................................................................................... 57 7.14.3 Energy syntax N°5 .......................................................................................................... 57 7.14.4 Energy syntax N°7 .......................................................................................................... 57 7.14.5 Energy syntax N°8 .......................................................................................................... 57 7.14.6 Energy syntax N°9 .......................................................................................................... 58 7.14.7 Energy syntax N°10 ........................................................................................................ 58 7.14.8 Energy syntax N°13 ........................................................................................................ 58 7.14.9 Energy syntax N°14 ........................................................................................................ 58 7.14.10 Energy syntax N°15 .................................................................................................... 58 7.14.11 Energy syntax N°16 .................................................................................................... 58 7.14.12 Energy syntax N°17 .................................................................................................... 58 7.14.13 Energy syntax N°18 .................................................................................................... 58 7.15 n-polytopes in 풁ퟕ .................................................................................................................. 58 7.16 Closest neighbour lattice points in 풁ퟕ for the quantity “energy “ ....................................... 61 7.17 Grassmann algebra of 풁ퟕ over 풁 for classification of physical quantities ............................ 62 8 Dimensional exploration of physics equations using dimensionless products ............................. 64 8.1 Dimensional analysis ............................................................................................................. 64 8.2 Buckingham 흅 theorem ........................................................................................................ 64 8.3 Dimensional matrix for SI units ............................................................................................. 64 8.4 Dimensional exploration of “a particle in a box “ ................................................................ 64 8.4.1 흅ퟏ .................................................................................................................................. 66 8.4.2 흅ퟐ .................................................................................................................................. 66 8.4.3 흅ퟑ .................................................................................................................................. 66 8.4.4 흅ퟒ .................................................................................................................................. 66 8.4.5 흅ퟓ .................................................................................................................................. 66 8.4.6 흅ퟔ .................................................................................................................................. 67 8.4.7 Approximation of 흎흅ퟏ, 흅ퟐ, 흅ퟑ, 흅ퟒ, 흅ퟓ, 흅ퟔ = ퟎ ......................................................... 67 8.4.8 Relations involving the dilution coefficient ................................................................... 70 8.4.9 Dimensional exploration of total angular momentum J ............................................... 71 8.4.10 Interaction of external fields on free particles .............................................................. 72 8.5 Dimensional exploration of “vacuum states”........................................................................ 73 8.6 Dimensional exploration of “a box containing charged particles” ....................................... 73 8.7 Dimensional exploration of “Casimir force” ......................................................................... 74 3 8.8 Dimensional exploration of “a rotating body” ..................................................................... 74 8.9 Parametric “dimensional exploration” of physics equations ................................................ 74 8.9.1 Solution for the quantity “Length” as function of the parametric set 풉, 풄ퟎ, 풎ퟎ, 푮 ..... 75 8.9.2 Solution for the quantity “Energy” as function of the parametric set 풉, 풄ퟎ, 풎ퟎ, 푮 ..... 76 8.9.3 Solution for the quantity “Force” as function of the parametric set 풉, 풄ퟎ, 풎ퟎ, 푮 ....... 77 8.9.4 Solution for the quantity “Length” as function of the parametric set 흁ퟎ, 휺ퟎ, 퐞, 퐆....... 79 8.9.5 Solution for the quantity “Frequency” as function of the parametric set 흁ퟎ, 휺ퟎ, 퐞, 퐆 . 79 8.9.6 Solution for the quantity “Energy” as function of the parametric set 흁ퟎ, 휺ퟎ, 퐞, 퐆....... 79 8.9.7 Solution for the quantity “Magnetic moment” as function of the parametric set 흁ퟎ, 휺ퟎ,
Load more

Recommended publications
  • Dimensional Analysis and the Theory of Natural Units
    LIBRARY TECHNICAL REPORT SECTION SCHOOL NAVAL POSTGRADUATE MONTEREY, CALIFORNIA 93940 NPS-57Gn71101A NAVAL POSTGRADUATE SCHOOL Monterey, California DIMENSIONAL ANALYSIS AND THE THEORY OF NATURAL UNITS "by T. H. Gawain, D.Sc. October 1971 lllp FEDDOCS public This document has been approved for D 208.14/2:NPS-57GN71101A unlimited release and sale; i^ distribution is NAVAL POSTGRADUATE SCHOOL Monterey, California Rear Admiral A. S. Goodfellow, Jr., USN M. U. Clauser Superintendent Provost ABSTRACT: This monograph has been prepared as a text on dimensional analysis for students of Aeronautics at this School. It develops the subject from a viewpoint which is inadequately treated in most standard texts hut which the author's experience has shown to be valuable to students and professionals alike. The analysis treats two types of consistent units, namely, fixed units and natural units. Fixed units include those encountered in the various familiar English and metric systems. Natural units are not fixed in magnitude once and for all but depend on certain physical reference parameters which change with the problem under consideration. Detailed rules are given for the orderly choice of such dimensional reference parameters and for their use in various applications. It is shown that when transformed into natural units, all physical quantities are reduced to dimensionless form. The dimension- less parameters of the well known Pi Theorem are shown to be in this category. An important corollary is proved, namely that any valid physical equation remains valid if all dimensional quantities in the equation be replaced by their dimensionless counterparts in any consistent system of natural units.
    [Show full text]
  • Chapter 5 Dimensional Analysis and Similarity
    Chapter 5 Dimensional Analysis and Similarity Motivation. In this chapter we discuss the planning, presentation, and interpretation of experimental data. We shall try to convince you that such data are best presented in dimensionless form. Experiments which might result in tables of output, or even mul- tiple volumes of tables, might be reduced to a single set of curves—or even a single curve—when suitably nondimensionalized. The technique for doing this is dimensional analysis. Chapter 3 presented gross control-volume balances of mass, momentum, and en- ergy which led to estimates of global parameters: mass flow, force, torque, total heat transfer. Chapter 4 presented infinitesimal balances which led to the basic partial dif- ferential equations of fluid flow and some particular solutions. These two chapters cov- ered analytical techniques, which are limited to fairly simple geometries and well- defined boundary conditions. Probably one-third of fluid-flow problems can be attacked in this analytical or theoretical manner. The other two-thirds of all fluid problems are too complex, both geometrically and physically, to be solved analytically. They must be tested by experiment. Their behav- ior is reported as experimental data. Such data are much more useful if they are ex- pressed in compact, economic form. Graphs are especially useful, since tabulated data cannot be absorbed, nor can the trends and rates of change be observed, by most en- gineering eyes. These are the motivations for dimensional analysis. The technique is traditional in fluid mechanics and is useful in all engineering and physical sciences, with notable uses also seen in the biological and social sciences.
    [Show full text]
  • Three-Dimensional Analysis of the Hot-Spot Fuel Temperature in Pebble Bed and Prismatic Modular Reactors
    Transactions of the Korean Nuclear Society Spring Meeting Chuncheon, Korea, May 25-26 2006 Three-Dimensional Analysis of the Hot-Spot Fuel Temperature in Pebble Bed and Prismatic Modular Reactors W. K. In,a S. W. Lee,a H. S. Lim,a W. J. Lee a a Korea Atomic Energy Research Institute, P. O. Box 105, Yuseong, Daejeon, Korea, 305-600, [email protected] 1. Introduction thousands of fuel particles. The pebble diameter is 60mm High temperature gas-cooled reactors(HTGR) have with a 5mm unfueled layer. Unstaggered and 2-D been reviewed as potential sources for future energy needs, staggered arrays of 3x3 pebbles as shown in Fig. 1 are particularly for a hydrogen production. Among the simulated to predict the temperature distribution in a hot- HTGRs, the pebble bed reactor(PBR) and a prismatic spot pebble core. Total number of nodes is 1,220,000 and modular reactor(PMR) are considered as the nuclear heat 1,060,000 for the unstaggered and staggered models, source in Korea’s nuclear hydrogen development and respectively. demonstration project. PBR uses coated fuel particles The GT-MHR(PMR) reactor core is loaded with an embedded in spherical graphite fuel pebbles. The fuel annular stack of hexahedral prismatic fuel assemblies, pebbles flow down through the core during an operation. which form 102 columns consisting of 10 fuel blocks PMR uses graphite fuel blocks which contain cylindrical stacked axially in each column. Each fuel block is a fuel compacts consisting of the fuel particles. The fuel triangular array of a fuel compact channel, a coolant blocks also contain coolant passages and locations for channel and a channel for a control rod.
    [Show full text]
  • Units of Measurement and Dimensional Analysis
    Measurements and Dimensional Analysis POGIL ACTIVITY.2 Name ________________________________________ POGIL ACTIVITY 2 Units of Measurement and Dimensional Analysis A. Units of Measurement- The SI System and Metric System here are myriad units for measurement. For example, length is reported in miles T or kilometers; mass is measured in pounds or kilograms and volume can be given in gallons or liters. To avoid confusion, scientists have adopted an international system of units commonly known as the SI System. Standard units are called base units. Table A1. SI System (Systéme Internationale d’Unités) Measurement Base Unit Symbol mass gram g length meter m volume liter L temperature Kelvin K time second s energy joule j pressure atmosphere atm 7 Measurements and Dimensional Analysis POGIL. ACTIVITY.2 Name ________________________________________ The metric system combines the powers of ten and the base units from the SI System. Powers of ten are used to derive larger and smaller units, multiples of the base unit. Multiples of the base units are defined by a prefix. When metric units are attached to a number, the letter symbol is used to abbreviate the prefix and the unit. For example, 2.2 kilograms would be reported as 2.2 kg. Plural units, i.e., (kgs) are incorrect. Table A2. Common Metric Units Power Decimal Prefix Name of metric unit (and symbol) Of Ten equivalent (symbol) length volume mass 103 1000 kilo (k) kilometer (km) B kilogram (kg) Base 100 1 meter (m) Liter (L) gram (g) Unit 10-1 0.1 deci (d) A deciliter (dL) D 10-2 0.01 centi (c) centimeter (cm) C E 10-3 0.001 milli (m) millimeter (mm) milliliter (mL) milligram (mg) 10-6 0.000 001 micro () micrometer (m) microliter (L) microgram (g) Critical Thinking Questions CTQ 1 Consult Table A2.
    [Show full text]
  • International System of Units (SI)
    International System of Units (SI) National Institute of Standards and Technology (www.nist.gov) Multiplication Prefix Symbol factor 1018 exa E 1015 peta P 1012 tera T 109 giga G 106 mega M 103 kilo k 102 * hecto h 101 * deka da 10-1 * deci d 10-2 * centi c 10-3 milli m 10-6 micro µ 10-9 nano n 10-12 pico p 10-15 femto f 10-18 atto a * Prefixes of 100, 10, 0.1, and 0.01 are not formal SI units From: Downs, R.J. 1988. HortScience 23:881-812. International System of Units (SI) Seven basic SI units Physical quantity Unit Symbol Length meter m Mass kilogram kg Time second s Electrical current ampere A Thermodynamic temperature kelvin K Amount of substance mole mol Luminous intensity candela cd Supplementary SI units Physical quantity Unit Symbol Plane angle radian rad Solid angle steradian sr From: Downs, R.J. 1988. HortScience 23:881-812. International System of Units (SI) Derived SI units with special names Physical quantity Unit Symbol Derivation Absorbed dose gray Gy J kg-1 Capacitance farad F A s V-1 Conductance siemens S A V-1 Disintegration rate becquerel Bq l s-1 Electrical charge coulomb C A s Electrical potential volt V W A-1 Energy joule J N m Force newton N kg m s-2 Illumination lux lx lm m-2 Inductance henry H V s A-1 Luminous flux lumen lm cd sr Magnetic flux weber Wb V s Magnetic flux density tesla T Wb m-2 Pressure pascal Pa N m-2 Power watt W J s-1 Resistance ohm Ω V A-1 Volume liter L dm3 From: Downs, R.J.
    [Show full text]
  • Planck Dimensional Analysis of Big G
    Planck Dimensional Analysis of Big G Espen Gaarder Haug⇤ Norwegian University of Life Sciences July 3, 2016 Abstract This is a short note to show how big G can be derived from dimensional analysis by assuming that the Planck length [1] is much more fundamental than Newton’s gravitational constant. Key words: Big G, Newton, Planck units, Dimensional analysis, Fundamental constants, Atomism. 1 Dimensional Analysis Haug [2, 3, 4] has suggested that Newton’s gravitational constant (Big G) [5] can be written as l2c3 G = p ¯h Writing the gravitational constant in this way helps us to simplify and quantify a long series of equations in gravitational theory without changing the value of G, see [3]. This also enables us simplify the Planck units. We can find this G by solving for the Planck mass or the Planck length with respect to G, as has already been done by Haug. We will claim that G is not anything physical or tangible and that the Planck length may be much more fundamental than the Newton’s gravitational constant. If we assume the Planck length is a more fundamental constant than G,thenwecanalsofindG through “traditional” dimensional analysis. Here we will assume that the speed of light c, the Planck length lp, and the reduced Planck constanth ¯ are the three fundamental constants. The dimensions of G and the three fundamental constants are L3 [G]= MT2 L2 [¯h]=M T L [c]= T [lp]=L Based on this, we have ↵ β γ G = lp c ¯h L3 L β L2 γ = L↵ M (1) MT2 T T ✓ ◆ ✓ ◆ Based on this, we obtain the following three equations Lenght : 3 = ↵ + β +2γ (2) Mass : 1=γ (3) − Time : 2= β γ (4) − − − ⇤e-mail [email protected].
    [Show full text]
  • Department of Physics Notes on Dimensional Analysis and Units
    1 CSUC Department of Physics 301A Mechanics: Notes on Dimensional Analysis and Units I. INTRODUCTION Physics has a particular interest in those attributes of nature which allow comparison processes. Such qualities include e.g. length, time, mass, force, energy...., etc. By \comparison process" we mean that although we recognize that, say, \length" is an abstract quality, nonetheless, any two \lengths" may successfully be compared in a generally agreed upon manner yielding a real number which we sometimes, by custom, call their \ratio". It's crucial to realize that this outcome it isn't really a mathematical ratio since the participants aren't numbers at all, but rather completely abstract entities . viz. \Physical Extent in Space". Thus we undertake to represent physical qualities (i.e. certain aspects) of our system with real numbers. In general, we recognize that only `lengths' can be compared to `other lengths' etc - i.e. that the world divides into exclusive classes (e.g. `all lengths') of entities which can be compared to each other. We say that all the entities in any one class are `mutually comparable' with each other. These physical numbers will be our basic tools for expressing the relationships we observe in nature. As we proceed in our understanding of the physical world we will come to understand that any (and ultimately every !) properly expressed relationship (e.g. our theories) has several universal aspects of structure which we will study using what we may call \dimensional analysis". These structural aspects are of enormous importance and will be, as you progress, among the very first things you examine in any physical problem you encounter.
    [Show full text]
  • 3.1 Dimensional Analysis
    3.1 DIMENSIONAL ANALYSIS Introduction (For the Teacher).............................................................................................1 Answers to Activities 3.1.1-3.1.7........................................................................................8 3.1.1 Using appropriate unit measures..................................................................................9 3.1.2 Understanding Fundamental Quantities....................................................................14 3.1.3 Understanding unit definitions (SI vs Non-sI Units)................................................17 3.1.4 Discovering Key Relationships Using Fundamental Units (Equations)...................20 3.1.5 Using Dimensional Analysis for Standardizing Units...............................................24 3.1.6 Simplifying Calculations: The Line Method.............................................................26 3.1.7 Solving Problems with Dimensional Analysis ..........................................................29 INTRODUCTION (FOR THE TEACHER) Many teachers tell their students to solve “word problems” by “thinking logically” and checking their answers to see if they “look reasonable”. Although such advice sounds good, it doesn’t translate into good problem solving. What does it mean to “think logically?” How many people ever get an intuitive feel for a coluomb , joule, volt or ampere? How can any student confidently solve problems and evaluate solutions intuitively when the problems involve abstract concepts such as moles, calories,
    [Show full text]
  • [PDF] Dimensional Analysis
    Printed from file Manuscripts/dimensional3.tex on October 12, 2004 Dimensional Analysis Robert Gilmore Physics Department, Drexel University, Philadelphia, PA 19104 We will learn the methods of dimensional analysis through a number of simple examples of slightly increasing interest (read: complexity). These examples will involve the use of the linalg package of Maple, which we will use to invert matrices, compute their null subspaces, and reduce matrices to row echelon (Gauss Jordan) canonical form. Dimensional analysis, powerful though it is, is only the tip of the iceberg. It extends in a natural way to ideas of symmetry and general covariance (‘what’s on one side of an equation is the same as what’s on the other’). Example 1a - Period of a Pendulum: Suppose we need to compute the period of a pendulum. The length of the pendulum is l, the mass at the end of the pendulum bob is m, and the earth’s gravitational constant is g. The length l is measured in cm, the mass m is measured in gm, and the gravitational constant g is measured in cm/sec2. The period τ is measured in sec. The only way to get something whose dimensions are sec from m, g, and l is to divide l by g, and take the square root: [τ] = [pl/g] = [cm/(cm/sec2)]1/2 = [sec2]1/2 = sec (1) In this equation, the symbol [x] is read ‘the dimensions of x are ··· ’. As a result of this simple (some would say ‘sleazy’) computation, we realize that the period τ is proportional to pl/g up to some numerical factor which is usually O(1): in plain English, of order 1.
    [Show full text]
  • Dimensional Analysis
    Dimensional Analysis Taylor Dupuy November 14, 2013 Abstract Hannes Schenck explained this to me. 1 Units and Buckingham's Theorem Given a physical system there are basic units such as mass M, time T and length L and then there are \derived units" like speed S = LT −1, force F = MLT −2 and energy E = FL. Really a unit is derived from a collection of others if there is an algebraic dependence relation. For a given physical system (an experiment or thought experiment) one can take all the units you can measure (or more that will vary while you are considering them) and form an abelian group. For example with the units above if we chose the bijection M = (1; 0; 0), T = (0; 1; 0) and L = (0; 0; 1) then speed is just LT −1 = (1; −1; 0), force is (1; −2; 1) and energy is (1; 2; −1). Really the choice of which units are \derived" is quite arbitrary. All we really know is that we have a collection of units (for example M; T; L; S; F; E) and that they satisfy certain relations. There is a physical map from these units to the physical world for which one has prescribed dimensions. A dimensionless unit is one which is in the kernel of this map. In our example, −1 −1 −2 π1 = SL T is such an element (there are acually two more π2 = F MLT −1 2 −2 and π3 = E ML T ). Note that the free abelian group on our parameters is generated by the fundamental units together with the dimensionless ones.
    [Show full text]
  • Framework for the Strategic Management of Dimensional Variability of Structures in Modular Construction
    Framework for the Strategic Management of Dimensional Variability of Structures in Modular Construction by Christopher Rausch A thesis presented to the University of Waterloo in the fulfillment of the thesis requirement for the degree of Master of Applied Science in Civil Engineering Waterloo, Ontario, Canada, 2016 © Christopher Rausch 2016 Author’s Declaration I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. ii Abstract Challenges in construction related to dimensional variability exist because producing components and assemblies that have perfect compliance to dimensions and geometry specified in a design is simply not feasible. The construction industry has traditionally adopted tolerances as a way of mitigating these challenges. But what happens when tolerances are not appropriate for managing dimensional variability? In applications requiring very precise dimensional coordination, such as in modular construction, the use of conventional tolerances is frequently insufficient for managing the impacts of dimensional variability. This is evident from the literature and numerous industry examples. Often, there is a lack of properly understanding the rationale behind tolerances and about how to derive case specific allowances. Literature surrounding the use of tolerances in construction indicates that dimensional variability is often approached in a trial and error manner, waiting for conflicts and challenges to first arise, before developing appropriate solutions. While this is time consuming, non-risk averse, prone to extensive rework and very costly in conventional construction, these issues only intensify in modular construction due to the accumulation of dimensional variability, the geometric complexity of modules, and discrepancy between module production precision and project site dimensional precision.
    [Show full text]
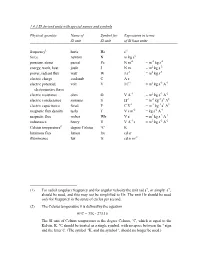
  • 1.4.3 SI Derived Units with Special Names and Symbols
    1.4.3 SI derived units with special names and symbols Physical quantity Name of Symbol for Expression in terms SI unit SI unit of SI base units frequency1 hertz Hz s-1 force newton N m kg s-2 pressure, stress pascal Pa N m-2 = m-1 kg s-2 energy, work, heat joule J N m = m2 kg s-2 power, radiant flux watt W J s-1 = m2 kg s-3 electric charge coulomb C A s electric potential, volt V J C-1 = m2 kg s-3 A-1 electromotive force electric resistance ohm Ω V A-1 = m2 kg s-3 A-2 electric conductance siemens S Ω-1 = m-2 kg-1 s3 A2 electric capacitance farad F C V-1 = m-2 kg-1 s4 A2 magnetic flux density tesla T V s m-2 = kg s-2 A-1 magnetic flux weber Wb V s = m2 kg s-2 A-1 inductance henry H V A-1 s = m2 kg s-2 A-2 Celsius temperature2 degree Celsius °C K luminous flux lumen lm cd sr illuminance lux lx cd sr m-2 (1) For radial (angular) frequency and for angular velocity the unit rad s-1, or simply s-1, should be used, and this may not be simplified to Hz. The unit Hz should be used only for frequency in the sense of cycles per second. (2) The Celsius temperature θ is defined by the equation θ/°C = T/K - 273.15 The SI unit of Celsius temperature is the degree Celsius, °C, which is equal to the Kelvin, K.
    [Show full text]