DOCSLIB.ORG

Review of Phasor Notation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Review of Phasor Notation Chapter 1 Review of Phasor Notation ECE 130a Introduction to Electromagnetics ejjq =+cosq sinq Complex Vectors and Time Harmonic Representation (Chapter 1.5, 1.6 Text) Complex Numbers Imaginary i) Rectangular/Cartesian Representation cajb=+ b ii) Polar Representation c φ jf 22 Real cce= , where cab=+ a = −1 b f tan dia cajbcec=+ =jf =cosff + jc sin real part imaginary part magnitude phase iii) Addition/Subtraction Cartesian representation most convenient cajb=+ dejh=+ Then: cd+=a ae ++f jbha +f −= −+ − cda aef jbha f iv) Multiplication/Division 2 Note that afj =−1 22 2 cc* =+= a b c , =− where cajb* , the complex conjugate. v) Cartesian Representation cd=+afafafaf a jb e + jh = ae − bh + j ah + be + + − ++ − c = ajb= ajbejh= afafae bh j be ah + + − 22+ d ejh ejhejh eh vi) Polar Representation (more convenient for multiplication and division) c j ff− jf jf j diff+ c di12 cce= 1 dde= 2 cd= c d e 12 = e d d vii) Complex Representation of Time-harmonic Scalars Consider: vtaf=+ Acosbgwfo t amplitude phase angular/radian 1 frequency magnitude aaa$$$= * 2 ωπ= $ and 2 f amplitude Re a1 radian frequency frequency Sinusoidally Time Varying Fields (1.6 Text) F p I 1) fA=+=+cosafwf t110 cos 120 p t H 4 K p FNote: radians =∞45 I H 4 K is a scalar field that depends on time only, but not on position (location). This is not a wave. For example, this is the voltage in any electric household plug. Note that the phase f simply alters the starting point. p t Fin units of I H wK voltage The circular frequency ωπ= 2 f , where f is the frequency in Hz. Here, f = 60 hertz (Hz) and ωπ==120 377 rad / sec 2) Waves -- travelling waves (main subject of this course) z vV=-cosw F t I o H vK =-Vtkzo cosaw f or Vtzo cosawb- f F z I =-Vftcos2p →+λ o H l K Repeats zz wp22f p k aor bf ∫= = propagation constant vv l v = λ f λ = wavelength 21π T ≡≡≡period v = phase velocity ω f π 2 = λ β F p I z G in units of J H b K with t = 0 This is a scalar traveling wave. 3) Vector Travelling Waves -- electromagnetic waves Examples: r F yI (i)EeE=-$ cosww t =-eE$ cosa t kyf xoH vK xo (x-oriented field, + y propagation) r F 1 $$3 I (ii)Ee=+G xyo eEtkzJ cosafw - H 2 2 K $ y eE $$1 3 $ 3 eeEx=+ e y 1 2 2 2 x 1 r 2 $ ∞ (iii)EeE=-+xocoscw tkz45 h (x-oriented, + z propagation) r p p (iv)HeH=-$ sinF xtzeHI cosafwb-+$ cosF xtzI sin afwb- xoH a K z1 H a K (waveguide example) Example: (x-directed planewave, - y propagation) r Eytaf, =++ e$ 100coscwb t y 45 ∞ h ω x = β L y ∞ O v =+et$ 100cos w F I + 45 x NM H vK QP This is a vector travelling wave field. t = 0 p t = 4w F p I y G in units of J H b K Propagates in the − y direction At ty=+045:coscb ∞ h p At ty=+=-:coschbb90 ∞ sin y 4w Note that this vector field: $ (i) always points in the ex direction (reverses, of course). (ii) propagates in the y direction. (iii)spatially depends only on the y coordinate (which is the direction of propaga- tion). z z uniform y in x-y y plane x x The magnitude E, that is, the density of these lines (or the length of the arrows), var- ies sinusoidally, both in time and in the variable y direction of propagation. Ex 100 π 3π 3 ω ω At y =− λ t 8 2π ω r 3 23p p At y =− λ : Ee=-+$ cos100 Fw t l I 8 x H l 84K p =-etet$ 100cosFw I = $ 100sinw xxH 2 K r p At y = 0: Ee=+$ cos100 Fw t I x H 4 K 100 π 3π ω ω t 2π ω Method of Phasors (“Set your phasors on ‘Stun,’ Mr. Spock!”) Background material needed: Review of complex algebra Eulers Law: exjxjx =+cos sin Reexexjx==cos , Im jx sin Suppose we have a field that varies sinusoidally in time and/or space. For a scalar field, voltage, for example, we have: = ω vVo cos t (a sinusoidal voltage) vV=-o cosaw tkzf (a voltage wave on a transmission line) These are real measurable quantities. We represent them by writing as follows: jtw vVe= Remro Now we do either of (a) or (b): = jtω (a) Drop “Re ”. The remaining v Veo is called the complex voltage (includ- ing time dependence) or voltage phasor (including time dependence). jtw jtω (b) vVe= Remro Drop “Re ” and “e ” = The resultant v Vo is called the (complex) phasor. Note that, for this example, the complex phasor happens to be real. (PHASORS are written in bold type- face.) If v =+Vto cosawff jtafwf+ jtwf j ==ReVeo Re Veo e jjtfw = Re Veo e jf Veo is a complex quantity in polar representation. Im ejjf =+cosff sin jf 22 Vo e =+=cosff sin 1 φ Re Graphical Picture of Complex Fields Consider a vector field with harmonic time dependence: r p L j O $ ∞ $ jtw 6 EeE=+∫xocoscw t30 h Re M eEee xo P N Q p j $ ∞ 6 This is another notation for eExo– 30 e . r $ ∞ jtw Complex form: EeE=–xo30 e phasor amplitude (also a vector) If we picture the entire time dependent complex field in the complex plane, we see that it rotates at angular velocity ω . π Im ω t = = 3ω t 0 Eo ° 30 Re π = t ω Note that the direction of the complex field on this complex plane has no relation- $ ship to its direction in real physical space, which here is constant ex . The entire complex field, including e jtω time dependence, is often called “Rotating Phasor.” The real field is the projection on the Re axis. Amplitude, Time Average, Mean Square and Root Mean Square (a) Amplitude is the maximum value of the time oscillation (real number). r $ (i) Ee=-+x100cosafwbf t z real r $ jf E = eex100 phasor Amplitude is 100 rr 1 2 Amplitude ≡ magnitude of phasor ≡ E = EE* −+ββ (ii) v =−100eejz 100 jz 2 waves in opposite direction, phasor form L eejx- - jx O MUse sin x = P N 2 j Q 200 j =-ee+-jzbb - jz =-200 jzsin b ⇐ This is the phasor 2 j (simplified). Amplitude of the total wave is v =-200jzsinbbbb =afaf - 200 jz sin 200 jz sin = 200 sin z function of z! Now, real form vzta ,sinsinf = 200 bw z t because: vzta ,sinf =-Re 200 jb zejtw =−Re 200jzsinβω cos t + 200 sinβ zt sinω = βω 200sinzt sin arrows show time oscillations z (b) Time average of a harmonic quantity is always zero. jf ← vta f =+ Vo cosawf t f v = Veo phasor 1 T = 1 vtaf=+∫Vto cos awf f 0 T T z0 f (c) Mean square is not zero. T 221 2 vtaf=+Vtdto cos awf f T z0 T 112 L 1 O =++Vtdto cosaf22wf T z0 NM2 2 QP V 2 = o 2 Using phasors for v 2 cannot give correct answers since phasors are not valid for a nonlinear situation. Try it and see: 222= ω 2222jtwf+ j vVo cos t , but v = Veo Does not give cos 2 when real part is taken for the time average. But the following “trick” works: For the time average: (Note: It gives only the time average.) 1 1 V 2 v2() t==Revv * Re Vejff Ve- jo = 2 22o o (This works for vector phasors, too!) r $$ If: E =+eExx eE yy r rr 2 1 Etza ,*f = Re diEE◊ Vector “dot” product r 2 EEee= - jkz $ A A o x phasor The Mean Square is related to Average Power (averaged over whole cycles). The same “trick” works for any other second order quantity. 1 Note: The""Re is necessary here, vtitafaf = Re vi* 2 since v andi may have a phase difference. (d) Root Mean Square (RMS) 2 vt2a f or Eta f 1 For harmonic fields, RMS value = amplitude. 2 Example: r If: Ee=-$ 100cosafwb t z r r cylindrical coordinates arz,,f f $ He=--∞f 03.cosafwb t z 60 rr Calculate EH¥ , using both real fields and phasors. Solution: (a) Using real fields rr $ EH¥= ez 30cosafawb t - z cos wb t - z -∞ 60 f 1 Use product of cosAB◊ cos=-++mr cosafaf ABAB cos rr 2 EH¥= e$ cos ∞+ cos1560af 2wb t - 2 z -∞ 60 rrz $ EH¥= ez 75. + 0 (b) Using phasors r $ E = er100 Phasors correspondingrr to p rr rr r - j 1 $ 3 the real Etza ,,f Htza ,f EH¥=RediEH ¥* H = eef 03. 2 p + j 1 $ 3 EH¥=* eez 15◊ 2 1 Re EH¥=* ee$ 15cos 60 ∞=$ 7. 5 2 zz Phasor examples with waves (1) Space dependence is due to propagation only (a) Uniform plane EM wave -- vector (b) Transmission line wave -- scalar voltage or current (1a) Propagation is only in one direction r $ R F z I U $ Real field: Eztaf, =- eExocosSwf t + V =-+eE xocos a wbf t z f T H vK W ω ω Propagation is in +z$ direction β = v = v β r $ jtafwbf-+ z Complex field: Ezta , f = eEexo $ jf jtafwb- z = eEexo e Phasor field: (two options possible) jtafwb- z (i) Drop entire e dependence r Phasor:E = eEe$ jf (algebraic)∫–eE$ f (schematic) r xo xo $$∞∞j 30 For example, E =–∫eeexx100 30 100 r p $ jtdiwb-+ z 6 Etzaf, = Re ex 100 e $ =-+∞etzx 100cosafwb 30 Another example: jj=+cosff sin , when f =∞90 r a f $$ E ==–∞ejyy50 e 50 90 r p $$jtafwb- z jtchwb-+ z 2 Etzaf, ==Re ey 50 je ey Re 50 e $ $ =-50etzetzyysinafwb - = 50cos a wb - + 90 ∞ f r Another example: E =-c eje$$h100 r xy $$jtafwb- z Etzaf, =-Re 100ch exy jee $ $ =-+-100 etzetzxycosawbf sin a wbf rr 2 1 1 2 $$$$ e ==-+Re 2 EE◊◊* 2af100 chch exyxy je e je 1 22 =+=2afafaf100 1 1 100 (ii) Drop only e jtω dependence r Eztaf, =-+ eE$ cos awbf t z f r xo jtafwbf-+ z Eztaf, = e$ Re Ee r xo $ -+jzjbf E = eEexo We can see that − βz and f both are phases.
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • About the Phasor Pathways in Analogical Amplitude Modulations
    About the Phasor Pathways in Analogical Amplitude Modulations H.M. de Oliveira1, F.D. Nunes1 ABSTRACT Phasor diagrams have long been used in Physics and Engineering. In telecommunications, this is particularly useful to clarify how the modulations work. This paper addresses rotating phasor pathways derived from different standard Amplitude Modulation Systems (e.g. A3E, H3E, J3E, C3F). A cornucopia of algebraic curves is then derived assuming a single tone or a double tone modulation signal. The ratio of the frequency of the tone modulator (fm) and carrier frequency (fc) is considered in two distinct cases, namely: fm/fc<1 and fm/fc 1. The geometric figures are some sort of Lissajours figures. Different shapes appear looking like epicycloids (including cardioids), rhodonea curves, Lemniscates, folium of Descartes or Lamé curves. The role played by the modulation index is elucidated in each case. Keyterms: Phasor diagram, AM, VSB, Circular harmonics, algebraic curves, geometric figures. 1. Introduction Classical analogical modulations are a nearly exhausted subject, a century after its introduction. The first approach to the subject typically relies on the case of transmission of a single tone (for the sake of simplicity) and establishes the corresponding phasor diagram. This furnishes a straightforward interpretation, which is quite valuable, especially with regard to illustrating the effects of the modulation index, overmodulation effects, and afterward, distinctions between AM and NBFM. Often this presentation is rather naïf. Nice applets do exist to help the understanding of the phasor diagram [1- 4]. However ... Without further target, unpretentiously, we start a deeper investigating the dynamic phasor diagram with the aim of building applets or animations that illustrates the temporal variation of the magnitude of the amplitude modulated phasor.
    [Show full text]
  • Correspondence Between Phasor Transforms and Frequency Response Function in Rlc Circuits
    CORRESPONDENCE BETWEEN PHASOR TRANSFORMS AND FREQUENCY RESPONSE FUNCTION IN RLC CIRCUITS Hassan Mohamed Abdelalim Abdalla Polytechnic Department of Engineering and Architecture, University of Studies of Udine, 33100 Udine, Italy. E-mail: [email protected] Abstract: The analysis of RLC circuits is usually made by considering phasor transforms of sinusoidal signals (characterized by constant amplitude, period and phase) that allow the calculation of the AC steady state of RLC circuits by solving simple algebraic equations. In this paper I try to show that phasor representation of RLC circuits is analogue to consider the frequency response function (commonly designated by FRF) of the total impedance of the circuit. In this way I derive accurate expressions for the resonance and anti-resonance frequencies and their corresponding values of impedances of the parallel and series RLC circuits respectively, notwithstanding the presence of damping effects. Keywords: Laplace transforms, phasors, Frequency response function, RLC circuits. 1. Introduction and mathematical background RLC circuits have many applications as oscillator circuits described by a second-order differential equation. The three circuit elements, resistor R, inductor L and capacitor C can be combined in different manners. All three elements in series or in parallel are the simplest and most straightforward to analyze. RLC circuits are analyzed mathematically in the phasor domain instead of solving differential equations in the time domain. Generally, a time-dependent sinusoidal function is expressed in the following way è [1]: () (1.1) where is the amplitude, is the angular frequency and is the initial phase of . () = sin ( + ) The medium value of is given by: () () (1.2) 1 2 = |()| = where is the period of the sinusoidal function .
    [Show full text]
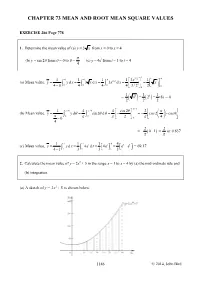
  • Chapter 73 Mean and Root Mean Square Values
    CHAPTER 73 MEAN AND ROOT MEAN SQUARE VALUES EXERCISE 286 Page 778 1. Determine the mean value of (a) y = 3 x from x = 0 to x = 4 π (b) y = sin 2θ from θ = 0 to θ = (c) y = 4et from t = 1 to t = 4 4 3/2 4 44 4 4 1 1 11/2 13x 13 (a) Mean value, y= ∫∫ yxd3d3d= xx= ∫ x x= = x − 00 0 0 4 0 4 4 4 3/20 2 1 11 = 433=( 2) = (8) = 4 2( ) 22 π /4 1 ππ/4 4 /4 4 cos 2θπ 2 (b) Mean value, yy=dθ = sin 2 θθ d =−=−−cos 2 cos 0 π ∫∫00ππ24 π − 0 0 4 2 2 = – (01− ) = or 0.637 π π 144 1 144 (c) Mean value, y= yxd= 4ett d t = 4e = e41 − e = 69.17 41− ∫∫11 3 31 3 2. Calculate the mean value of y = 2x2 + 5 in the range x = 1 to x = 4 by (a) the mid-ordinate rule and (b) integration. (a) A sketch of y = 25x2 + is shown below. 1146 © 2014, John Bird Using 6 intervals each of width 0.5 gives mid-ordinates at x = 1.25, 1.75, 2.25, 2.75, 3.25 and 3.75, as shown in the diagram x 1.25 1.75 2.25 2.75 3.25 3.75 y = 25x2 + 8.125 11.125 15.125 20.125 26.125 33.125 Area under curve between x = 1 and x = 4 using the mid-ordinate rule with 6 intervals ≈ (width of interval)(sum of mid-ordinates) ≈ (0.5)( 8.125 + 11.125 + 15.125 + 20.125 + 26.125 + 33.125) ≈ (0.5)(113.75) = 56.875 area under curve 56.875 56.875 and mean value = = = = 18.96 length of base 4− 1 3 3 4 44 1 1 2 1 2x 1 128 2 (b) By integration, y= yxd = 2 x + 5 d x = +5 x = +20 −+ 5 − ∫∫11 41 3 3 31 3 3 3 1 = (57) = 19 3 This is the precise answer and could be obtained by an approximate method as long as sufficient intervals were taken 3.
    [Show full text]
  • Frequency Response = K − Ml
    Frequency Response 1. Introduction We will examine the response of a second order linear constant coefficient system to a sinusoidal input. We will pay special attention to the way the output changes as the frequency of the input changes. This is what we mean by the frequency response of the system. In particular, we will look at the amplitude response and the phase response; that is, the amplitude and phase lag of the system’s output considered as functions of the input frequency. In O.4 the Exponential Input Theorem was used to find a particular solution in the case of exponential or sinusoidal input. Here we will work out in detail the formulas for a second order system. We will then interpret these formulas as the frequency response of a mechanical system. In particular, we will look at damped-spring-mass systems. We will study carefully two cases: first, when the mass is driven by pushing on the spring and second, when the mass is driven by pushing on the dashpot. Both these systems have the same form p(D)x = q(t), but their amplitude responses are very different. This is because, as we will see, it can make physical sense to designate something other than q(t) as the input. For example, in the system mx0 + bx0 + kx = by0 we will consider y to be the input. (Of course, y is related to the expression on the right- hand-side of the equation, but it is not exactly the same.) 2. Sinusoidally Driven Systems: Second Order Constant Coefficient DE’s We start with the second order linear constant coefficient (CC) DE, which as we’ve seen can be interpreted as modeling a damped forced harmonic oscillator.
    [Show full text]
  • Complex Numbers and Phasor Technique
    RaoApp-Av3.qxd 12/18/03 5:44 PM Page 779 APPENDIX A Complex Numbers and Phasor Technique In this appendix, we discuss a mathematical technique known as the phasor technique, pertinent to operations involving sinusoidally time-varying quanti- ties.The technique simplifies the solution of a differential equation in which the steady-state response for a sinusoidally time-varying excitation is to be deter- mined, by reducing the differential equation to an algebraic equation involving phasors. A phasor is a complex number or a complex variable. We first review complex numbers and associated operations. A complex number has two parts: a real part and an imaginary part. Imag- inary numbers are square roots of negative real numbers. To introduce the con- cept of an imaginary number, we define 2-1 = j (A.1a) or ;j 2 =-1 (A.1b) 1 2 Thus, j5 is the positive square root of -25, -j10 is the negative square root of -100, and so on.A complex number is written in the form a + jb, where a is the real part and b is the imaginary part. Examples are 3 + j4 -4 + j1 -2 - j2 2 - j3 A complex number is represented graphically in a complex plane by using Rectangular two orthogonal axes, corresponding to the real and imaginary parts, as shown in form Fig.A.1, in which are plotted the numbers just listed. Since the set of orthogonal axes resembles the rectangular coordinate axes, the representation a + jb is 1 2 known as the rectangular form. 779 RaoApp-Av3.qxd 12/18/03 5:44 PM Page 780 780 Appendix A Complex Numbers and Phasor Technique Imaginary (3 ϩ j4) 4 (Ϫ4 ϩ j1) 1 Ϫ2 2 Ϫ 4 0 3 Real Ϫ2 (Ϫ2 Ϫj2) Ϫ3 Ϫ FIGURE A.1 (2 j3) Graphical representation of complex numbers in rectangular form.
    [Show full text]
  • Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
    Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions.
    [Show full text]
  • To Learn the Basic Properties of Traveling Waves. Slide 20-2 Chapter 20 Preview
    Chapter 20 Traveling Waves Chapter Goal: To learn the basic properties of traveling waves. Slide 20-2 Chapter 20 Preview Slide 20-3 Chapter 20 Preview Slide 20-5 • result from periodic disturbance • same period (frequency) as source 1 f • Longitudinal or Transverse Waves • Characterized by – amplitude (how far do the “bits” move from their equilibrium positions? Amplitude of MEDIUM) – period or frequency (how long does it take for each “bit” to go through one cycle?) – wavelength (over what distance does the cycle repeat in a freeze frame?) – wave speed (how fast is the energy transferred?) vf v Wavelength and Frequency are Inversely related: f The shorter the wavelength, the higher the frequency. The longer the wavelength, the lower the frequency. 3Hz 5Hz Spherical Waves Wave speed: Depends on Properties of the Medium: Temperature, Density, Elasticity, Tension, Relative Motion vf Transverse Wave • A traveling wave or pulse that causes the elements of the disturbed medium to move perpendicular to the direction of propagation is called a transverse wave Longitudinal Wave A traveling wave or pulse that causes the elements of the disturbed medium to move parallel to the direction of propagation is called a longitudinal wave: Pulse Tuning Fork Guitar String Types of Waves Sound String Wave PULSE: • traveling disturbance • transfers energy and momentum • no bulk motion of the medium • comes in two flavors • LONGitudinal • TRANSverse Traveling Pulse • For a pulse traveling to the right – y (x, t) = f (x – vt) • For a pulse traveling to
    [Show full text]
  • Resonance Beyond Frequency-Matching
    Resonance Beyond Frequency-Matching Zhenyu Wang (王振宇)1, Mingzhe Li (李明哲)1,2, & Ruifang Wang (王瑞方)1,2* 1 Department of Physics, Xiamen University, Xiamen 361005, China. 2 Institute of Theoretical Physics and Astrophysics, Xiamen University, Xiamen 361005, China. *Corresponding author. [email protected] Resonance, defined as the oscillation of a system when the temporal frequency of an external stimulus matches a natural frequency of the system, is important in both fundamental physics and applied disciplines. However, the spatial character of oscillation is not considered in the definition of resonance. In this work, we reveal the creation of spatial resonance when the stimulus matches the space pattern of a normal mode in an oscillating system. The complete resonance, which we call multidimensional resonance, is a combination of both the spatial and the conventionally defined (temporal) resonance and can be several orders of magnitude stronger than the temporal resonance alone. We further elucidate that the spin wave produced by multidimensional resonance drives considerably faster reversal of the vortex core in a magnetic nanodisk. Our findings provide insight into the nature of wave dynamics and open the door to novel applications. I. INTRODUCTION Resonance is a universal property of oscillation in both classical and quantum physics[1,2]. Resonance occurs at a wide range of scales, from subatomic particles[2,3] to astronomical objects[4]. A thorough understanding of resonance is therefore crucial for both fundamental research[4-8] and numerous related applications[9-12]. The simplest resonance system is composed of one oscillating element, for instance, a pendulum. Such a simple system features a single inherent resonance frequency.
    [Show full text]
  • True RMS, Trueinrush®, and True Megohmmeter®
    “WATTS CURRENT” TECHNICAL BULLETIN Issue 09 Summer 2016 True RMS, TrueInRush®, and True Megohmmeter ® f you’re a user of AEMC® instruments, you may have come across the terms True IRMS, TrueInRush®, and/or True Megohmmeter ®. In this article, we’ll briefly define what these terms mean and why they are important to you. True RMS The most well-known of these is True RMS, an industry term for a method for calculating Root Mean Square. Root Mean Square, or RMS, is a mathematical concept used to derive the average of a constantly varying value. In electronics, RMS provides a way to measure effective AC power that allows you to compare it to the equivalent heating value of a DC system. Some low-end instruments employ a technique known as “average sensing,” sometimes referred to as “average RMS.” This entails multiplying the peak AC voltage or current by 0.707, which represents the decimal form of one over the square root of two. For electrical systems where the AC cycle is sinusoidal and reasonably undistorted, this can produce accurate and reliable results. Unfortunately, for other AC waveforms, such as square waves, this calculation can introduce significant inaccuracies. The equation can also be problematic when the AC wave is non-linear, as would be found in systems where the original or fundamental wave is distorted by one or more harmonic waves. In these cases, we need to apply a method known as “true” RMS. This involves a more generalized mathematical calculation that takes into consideration all irregularities and asymmetries that may be present in the AC waveform: In this equation, n equals the number of measurements made during one complete cycle of the waveform.
    [Show full text]
  • Lesson 1: Representation of Ac Voltages and Currents1
    1/22/2016 Lesson 1: Phasors and Complex Arithmetic ET 332b Ac Motors, Generators and Power Systems lesson1_et332b.pptx 1 Learning Objectives After this presentation you will be able to: Write time equations that represent sinusoidal voltages and currents found in power systems. Explain the difference between peak and RMS electrical quantities. Write phasor representations of sinusoidal time equations. Perform calculations using both polar and rectangular forms of complex numbers. lesson1_et332b.pptx 2 1 1/22/2016 Ac Analysis Techniques Time function representation of ac signals Time functions give representation of sign instantaneous values v(t) Vmax sin(t v ) Voltage drops e(t) Emax sin(t e ) Source voltages Currents i(t) Imax sin(t i ) Where Vmax = maximum ( peak) value of voltage Emax = maximum (peak) value of source voltage Imax = maximum (peak) value of current v, e, i = phase shift of voltage or current = frequency in rad/sec Note: =2pf lesson1_et332b.pptx 3 Ac Signal Representations Ac power system calculations use effective values of time waveforms (RMS values) Therefore: V E I V max E max I max RMS 2 RMS 2 RMS 2 1 Where 0.707 2 So RMS quantities can be expressed as: VRMS 0.707Vmax ERMS 0.707Emax IRMS 0.707Imax lesson1_et332b.pptx 4 2 1/22/2016 Ac Signal Representations Ac power systems calculations use phasors to represent time functions Phasor use complex numbers to represent the important information from the time functions (magnitude and phase angle) in vector form. Phasor Notation I I V VRMS RMS or or I I V VRMS RMS Where: VRMS, IRMS = RMS magnitude of voltages and currents = phase shift in degrees for voltages and currents lesson1_et332b.pptx 5 Ac Signal Representations Time to phasor conversion examples, Note all signal must be the same frequency Time function-voltage Find RMS magnitude v(t) 170sin(377t 30 ) VRMS 0.707170 120.2 V Phasor V 120.230 V Time function-current Find RMS magnitude i(t) 25sin(377t 20 ) IRMS 0.70725 17.7 A Phasor I 17.7 20 A Phase shift can be given in either radians or degrees.
    [Show full text]
  • Understanding What Really Happens at Resonance
    feature article Resonance Revealed: Understanding What Really Happens at Resonance Chris White Wood RESONANCE focus on some underlying principles and use these to construct The word has various meanings in acoustics, chemistry, vector diagrams to explain the resonance phenomenon. It thus electronics, mechanics, even astronomy. But for vibration aspires to provide a more intuitive understanding. professionals, it is the definition from the field of mechanics that is of interest, and it is usually stated thus: SYSTEM BEHAVIOR Before we move on to the why and how, let us review the what— “The condition where a system or body is subjected to an that is, what happens when a cyclic force, gradually increasing oscillating force close to its natural frequency.” from zero frequency, is applied to a vibrating system. Let us consider the shaft of some rotating machine. Rotor Yet this definition seems incomplete. It really only states the balancing is always performed to within a tolerance; there condition necessary for resonance to occur—telling us nothing will always be some degree of residual unbalance, which will of the condition itself. How does a system behave at resonance, give rise to a rotating centrifugal force. Although the residual and why? Why does the behavior change as it passes through unbalance is due to a nonsymmetrical distribution of mass resonance? Why does a system even have a natural frequency? around the center of rotation, we can think of it as an equivalent Of course, we can diagnose machinery vibration resonance “heavy spot” at some point on the rotor. problems without complete answers to these questions.
    [Show full text]