Studies of a Population of Stars: Mapping the Positions of Stars
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

I Nomi Delle Stelle
I nomi delle stelle Se state leggendo questa pagina perché volete acquistare il nome di una stella, visitate IAU Theme Buying Stars and Star Names. Altrimenti, proseguite con il testo sottostante. L'UAI intende delineare una distinzione tra i termini nome e designazione. In questo testo, così come in altre pubblicazioni dell'UAI, il nome si riferisce al termine (solitamente colloquiale) utilizzato per una stella nel linguaggio quotidiano, mentre la designazione è esclusivamente alfanumerica e viene usata quasi esclusivamente nei cataloghi ufficiali e nell'astronomia professionale. Storia dei cataloghi stellari La catalogazione delle stelle ha una lunga storia alle spalle. Sin dalla preistoria, culture e civiltà in tutto il mondo hanno dato dei propri nomi alle stelle più luminose e importanti nel cielo notturno. Attraversando le culture greca, latina e araba, alcuni nomi hanno subito pochi cambiamenti e altri sono in uso ancora oggi. Mentre l'astronomia si sviluppava e si evolveva nel corso dei secoli, sorgeva la necessità di un sistema di catalogazione universale, in base al quale le stelle più luminose (e quindi quelle più studiate) fossero conosciute secondo gli stessi appellativi, indipendentemente dal Paese o dalla cultura da cui provenivano gli astronomi. Per risolvere questo problema, gli astronomi durante il Rinascimento hanno tentato di produrre cataloghi stellari seguendo un insieme di regole. Il primo esempio, ancora oggi popolare, è stato introdotto da Johann Bayer nel suo atlante Uranometria del 1603. Bayer ha catalogato le stelle in ogni costellazione con lettere greche minuscole, seguendo l'ordine approssimativo della loro luminosità apparente, in modo che la stella più luminosa di una costellazione fosse solitamente (ma non sempre) etichettata come Alpha, la seconda più brillante fosse Beta, e così via. -

The Sky Tonight
MARCH POUTŪ-TE-RANGI HIGHLIGHTS Conjunction of Saturn and the Moon A conjunction is when two astronomical objects appear close in the sky as seen THE- SKY TONIGHT- - from Earth. The planets, along with the TE AHUA O TE RAKI I TENEI PO Sun and the Moon, appear to travel across Brightest Stars our sky roughly following a path called the At this time of the year, we can see the ecliptic. Each body travels at its own speed, three brightest stars in the night sky. sometimes entering ‘retrograde’ where they The brightness of a star, as seen from seem to move backwards for a period of time Earth, is measured as its apparent (though the backwards motion is only from magnitude. Pictured on the cover is our vantage point, and in fact the planets Sirius, the brightest star in our night sky, are still orbiting the Sun normally). which is 8.6 light-years away. Sometimes these celestial bodies will cross With an apparent magnitude of −1.46, paths along the ecliptic line and occupy the this star can be found in the constellation same space in our sky, though they are still Canis Major, high in the northern sky. millions of kilometres away from each other. Sirius is actually a binary star system, consisting of Sirius A which is twice the On March 19, the Moon and Saturn will be size of the Sun, and a faint white dwarf in conjunction. While the unaided eye will companion named Sirius B. only see Saturn as a bright star-like object (Saturn is the eighth brightest object in our Sirius is almost twice as bright as the night sky), a telescope can offer a spectacular second brightest star in the night sky, view of the ringed planet close to our Moon. -

As of December 2017
LIST OF NON‐REMITTING and/or NON‐REPORTING EMPLOYERS as of December 2017 NO PRO PEN EMPLOYER'S NAME 1 PRO II 6010001001 2 H MAINTENANCE & GENERAL SERVICES 2 PRO II 6010001240 8K CARWASH & VULCANIZING SHOP 3 PRO II 6000001180 A.S QUILANG ENTERPRISES 4 PRO II 6010000671 AGCOR AGRO‐VET TRADING 5 PRO II 6030000744 AGUA PLUS WATER REFILLING STATION 6 PRO II 6010001821 ALBANO MANPOWER SERVICES 7 PRO II 6030001022 ALCAR PHARMACEUTICAL 8 PRO II 6010000780 ALEX & IYA'S BAKERY 9 PRO II 6010000780 ALEX & IYA'S BAKERY 10 PRO II 6010001293 ALEX ALLAM COMPUTER SHOP 11 PRO II 6030002338 ALKALIFE NATURE'S WATER REFILLING STATION 12 PRO II 6000007914 ALLIN ENTERPRISES INC. 13 PRO II 6030002380 ALLIZWELL FURNITURE SHOP 14 PRO II 6010000879 AMADING AUTO CYCLE PARTS & ACCESSORIES 15 PRO II 6030001497 AMAZING KONILETS COMPUTER SYSTEM & GENERAL MERCHANDISE 16 PRO II 6030000936 AMAZING KONILETS COMPUTER SYSTEMS & GENERAL MERCHANDISE 17 PRO II 6010001259 AMC PHARMACY 18 PRO II 006000002782 ANGELIC SPA 19 PRO II 006000002782 ANGELIC SPA 20 PRO II 6010000677 ANITA C. UY PALAY & BUYING STATION 21 PRO II 6020000488 APPLE DRAGON INTERNET & COFFEEE BAR 22 PRO II 6030000781 AR CUARESMA‐MORALES GE TRADING 23 PRO II 6010001526 AREEJ RTW AND ACCESSORIES 24 PRO II 6000006062 ARIA ENTERTAINMENT RESORTS & DEV'T INC. 25 PRO II 6030000920 ARREOLA'S DRESS SHOP 26 PRO II 6000008717 ASZ PAYMENT SERVICES, REMITTANCE AND OTHERS 27 PRO II 6000001742 AYONEIL TRAVEL AND TOURS 28 PRO II 6010000877 B A DIAZ GENERAL MERCHANDISE 29 PRO II 6010000881 B P FERNANDEZ DRY GOODS 30 PRO II 6030002070 -

An Aboriginal Australian Record of the Great Eruption of Eta Carinae
Accepted in the ‘Journal for Astronomical History & Heritage’, 13(3): in press (November 2010) An Aboriginal Australian Record of the Great Eruption of Eta Carinae Duane W. Hamacher Department of Indigenous Studies, Macquarie University, NSW, 2109, Australia [email protected] David J. Frew Department of Physics & Astronomy, Macquarie University, NSW, 2109, Australia [email protected] Abstract We present evidence that the Boorong Aboriginal people of northwestern Victoria observed the Great Eruption of Eta (η) Carinae in the nineteenth century and incorporated the event into their oral traditions. We identify this star, as well as others not specifically identified by name, using descriptive material presented in the 1858 paper by William Edward Stanbridge in conjunction with early southern star catalogues. This identification of a transient astronomical event supports the assertion that Aboriginal oral traditions are dynamic and evolving, and not static. This is the only definitive indigenous record of η Carinae’s outburst identified in the literature to date. Keywords: Historical Astronomy, Ethnoastronomy, Aboriginal Australians, stars: individual (η Carinae). 1 Introduction Aboriginal Australians had a significant understanding of the night sky (Norris & Hamacher, 2009) and frequently incorporated celestial objects and transient celestial phenomena into their oral traditions, including the sun, moon, stars, planets, the Milky Way and Magellanic Clouds, eclipses, comets, meteors, and impact events. While Australia is home to hundreds of Aboriginal groups, each with a distinct language and culture, few of these groups have been studied in depth for their traditional knowledge of the night sky. We refer the interested reader to the following reviews on Australian Aboriginal astronomy: Cairns & Harney (2003), Clarke (1997; 2007/2008), Fredrick (2008), Haynes (1992; 2000), Haynes et al. -
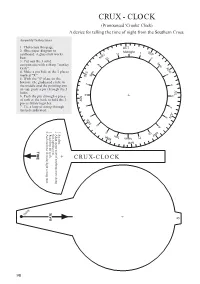
CRUX - CLOCK (Pronounced 'Crooks' Clock) a Device for Telling the Time of Night from the Southern Cross
CRUX - CLOCK (Pronounced 'Crooks' Clock) A device for telling the time of night from the Southern Cross. Assembly Instructions 1. Photocopy this page. OCT 2. Glue paper diagram to Midnight SEP cardboard. A glue-stick works 11 1 best. NOV 2 10 3. Cut out the 3 solid 3am components with a sharp "stanley 9 knife". AUG 4. Make a pin hole at the 3 places 4 8pm marked "X " DEC 5. With the "S" plate on the bottom, the graduated circle in 5 the middle and the pointing arm 7 on top, push a pin through the 3 JUL holes. 6 6. Push the pin through a piece 6 + of cork at the back to hold the 3 JAN pieces firmly together. 7 7. Tie a loop of string through 5 the hole indicated. JUN 8 4 FEB 3 9 MAY 4. Add one hour if on daylight saving time. 4. scale. 3. Read time off this sighting arm. Align major axis of southern cross along 2. 1. Set date. 10 2 11 1pm Noon MAR APR TIME + CRUX-CLOCK String + S DATE 98 HOW TO USE THE CRUX-CLOCK To Find the Time Axis 1. Set the date by rotating the graduated wheel. Acrux Gacrux It is a good idea at this stage to fix the wheel in place with a paper clip . 2. Hold the Crux-Clock at arms length by the Major string so that it hangs freely. 3. Face the Southern Cross and rotate the pointing arm so that it is parallel to the major axis of the Southern Cross. -

Astronomy Report Southern Cross Authors Maria Constanza Pavez Gabriela Constanza Rossi Consuelo Alizadeh Ruiz Ana Rojas
Astronomy Report Southern Cross Authors Maria Constanza Pavez Gabriela Constanza Rossi Consuelo Alizadeh Ruiz Ana Rojas (teacher) School Colegio Santa Marta Coquimbo Chile [email protected] Acknowledgements The authors acknowledge the support provided by the Chilean Astronomy Network (RChA, Red Chilena de Astronomía, http://www.rcha.cl) during the production of this work. The Spanish version of this report has been freed to the public domain under the terms of the License RChA. 2003 Object: areas of the Southern Cross and the Fly. Exposure: 30 minutes. Instrument: SMC Pentax-M lens 100 mm. F/2.8. Mount: CG-5 Camera: Pentax K-1000 Film: Kodak Ektachrome 200. Place: La Totorita camping, Mamalluca hill, IV region, Chile. Date: Sunday 10th February 2002, 02:38 h. Processing: Photoshop 5.0. I. Introduction Name: Southern Cross. Astronomical name: Crux. GENITIVE: Crucis. Common name: Southern Cross. This circumpolar constellation (always situated above the horizon) of the South Hemisphere, is located between the Centauri and the Fly constellations, just above the Polar Antarctic Circle and it is crossed by the Milky Way. The Crux is visible the whole year between 25 N and 90 S degrees of latitude, especially at early night from middle autumn and during the whole winter. This is why the Crux is not totally visible to all countries, and among those where it has the best visibility are: Chile, Argentina, Perú, Madagascar, Bolivia, Uruguay, etc. The Southern Cross is the smallest constellation, filling only 68 square degrees in the firmament and covering only the 5% of the biggest one, the Hidra. -

THE SKY TONIGHT Second Brightest Star in the Night Sky, Canopus
DECEMBER HAKIHEA Sailing in an Ocean of Stars HIGHLIGHTS The constellation of Carina is home to the THE SKY TONIGHT second brightest star in the night sky, Canopus. This brilliant beacon of light makes finding the TE ĀHUA O TE RAKI I TĒNEI PŌ constellation a breeze. Canopus has appeared in the mythology of many ancient cultures. Bright Stars This bright giant gets its modern name from For anyone new to the joys of star gazing, the mythological navigator of King Menelaus December heralds a beginner’s dream. Some of Sparta’s ship – some versions of the tale of the night sky’s brightest stars will illuminate suggest that Canopus was the helmsman or your experience. Orion, very much a summer pilot of the ship. constellation in Dunedin, will rise high in our northern night sky accompanied by his hunting Carina was once part of a much larger dogs – the constellations of Canis Major and constellation known as Argo Navis (the ship Argo) Canis Minor. Sirius, the ‘dog star’ impresses – three modern constellations formed this great with its luminosity; the brightest star in our ship in the sky, Carina the keel, Puppis the stern, night skies, it can be found at the head of and Vela the sails. In Greek mythology Argo was Canis Major (greater dog). the ship sailed by Jason and the Argonauts in search of the Golden Fleece. The origins of Argo For Harry Potter fans out there, you can Navis stem from ancient Greek, in the 1760s probably surmise where some of J K Rowling’s Nicolas Louis de Lacaille split the constellation inspiration came from! Orion itself boasts into its modern components. -

Aboriginal Astronomy: WA Focus
Aboriginal Astronomy: WA Focus by Pat Forster Celebrated through quilts Supported by references from the literature With web links to Aboriginal art 1 Published privately by Dr Patricia Forster 17 The Promenade Mount Pleasant Western Australia 6153 [email protected] https://patforsterblog.wordpress.com/ 02/08/2021 2 Index Sun ………………………………………………………………………3 Moon ……………………………………………………….………….11 Milky Way ……………………………………………….……………. 22 Southern Cross, Pointers and Coal Sack ……………………….….31 Pleiades .……..…………………………………………………….. 37 Orion ...........................……………………………………………...48 Magellanic Clouds …………………………………………………… 51 Aurora …………………………………………………………………. 52 Venus ………………………………………………………….....… 53 Star Navigation ………………………………………………………. 55 Meteors …………………………………………………………….56 References ……………………………………………………………63 Warning: Readers are respectfully advised that this paper contains names of people who are deceased. Web links to images are provided- if a webpage is no longer available, search on the artist and image names. 3 Sun Sun and Aboriginal Culture, by Pat Forster, 2021, 62 cm x 42 cm Quilt statement: The depiction of the Sun refers to relevant traditional cultural beliefs from Western Australia Aboriginal peoples. Characterisations include that the Sun is: the creator; giver of life; spirit carrying lighted wood; wife of Moon; mother of Venus; sun has fire, moon has light. The; sunup (dawn) and sundown (dusk) positions of the Sun were used to establish directions; Sun was a focus of increase rituals; and eclipses were feared. The quilted collage was inspired by a print of the acrylic-painting collage by JackieGuttusoDesigns https://www.etsy.com/au/shop/JackieGuttusoDesigns?ref=simple-shop-header- name&listing_id=558105433 Cotton fabrics; polyester-cotton, polyester, and metallic threads; cotton wadding. Machined raw- edge and turned edge applique; trapuntoed centre of the Sun, free-motion quilted text, machined straight-line quilting. -

STAR Brightnessin on the ‘Jewel Box’ in the Southern Cross (Hubble Space Telescope)
SCIENCE CONTENT/ TEACHER CURRICULUM LINK SHARING IDEAS AND RESOURCE OBSERVATIONS ABOUT THE STARS IN THE NIGHT SKY. EXTEND THEIR EXPERIENCES AND PERSONAL EXPLANATIONS OF THE NATURAL WORLD THROUGH EXPLORATION, PLAY, AND ASKING QUESTIONS. SEEK AND DESCRIBE STARDOME OBSERVATORY & PLANETARIUM SIMPLE PATTERNS IN PHYSICAL PHENOMENA. FACTS, RESOURCES AND ACTIVITIES ON... Even the faintest stars are not the same brightness as each other, when zooming STAR BRIGHTNESSin on the ‘Jewel Box’ in the Southern Cross (Hubble Space Telescope). Credit: ESO. Looking up at the stars at night we notice that they range from quite bright to very, very faint. Our automatic instinct is to assume the stars have different brightnesses, and not to think about how far away they are from us. But if we remember that our Sun is a star, and it appears hugely brighter than night time stars, then the distances to stars must also affect how bright they seem to us. Two stars that appear the same brightness at night may in fact be a faint star quite close and a bright star very far away. For example, the nearest star to our Sun is Alpha Centauri, which is 4.3 light-years* distant. If our Sun were at that distance, it would appear over 38 billion times fainter than in our daytime sky! In fact, it would be as faint as Procyon in the night sky, which is the main Absolute magnitude is a calculation of a star’s intrinsic star of the constellation Canis minoris (The Small Dog) brightness by adjusting its apparent magnitude to be at near the great constellation of Orion. -

This Online Essay Is an Extended Version of the Essay in the Printed-Edition Handbook, Containing All the Material of Its Print
This online essay is an extended version of the essay in the printed-edition Handbook, containing all the material of its printed- edition accompaniment, but adding material of its own. The accompanying online table is likewise an extended version of the printed-edition table, (a) with extra stars (the brightest 313, allowing for variability, where the printed edition has almost 30 fewer, allowing for variability), and (b) with additional remarks for most of the duplicated stars. The online essay and table try to address the needs of three kinds of serious amateur: amateurs who are also astrophysics students (whether or not enrolled formally at some campus); amateurs who, like many in RASC, assist in public outreach, through some form of lecturing; and amateurs who are planning their own private citizen-science observing runs, in the spirit of such “pro-am” organizations as AAVSO. Our online project, now a couple of years old, must be considered still in its early stages. We cannot claim to have fully satisfied the needs of our three constituencies. Above all, we cannot claim to have covered all the appropriate points from stellar- astronomy news in our “Remarks” column, important though news is to amateurs of all three types. We would hope in coming years to remedy our deficiencies in several ways, above all by relying more in our writing on recent primary-literature journal articles, and by making appropriate citations of the primary literature. Already at this early stage, we have tried to pick out a few tens of the more important recent journal articles. -

Brightest Stars : Discovering the Universe Through the Sky's Most Brilliant Stars / Fred Schaaf
ffirs.qxd 3/5/08 6:26 AM Page i THE BRIGHTEST STARS DISCOVERING THE UNIVERSE THROUGH THE SKY’S MOST BRILLIANT STARS Fred Schaaf John Wiley & Sons, Inc. flast.qxd 3/5/08 6:28 AM Page vi ffirs.qxd 3/5/08 6:26 AM Page i THE BRIGHTEST STARS DISCOVERING THE UNIVERSE THROUGH THE SKY’S MOST BRILLIANT STARS Fred Schaaf John Wiley & Sons, Inc. ffirs.qxd 3/5/08 6:26 AM Page ii This book is dedicated to my wife, Mamie, who has been the Sirius of my life. This book is printed on acid-free paper. Copyright © 2008 by Fred Schaaf. All rights reserved Published by John Wiley & Sons, Inc., Hoboken, New Jersey Published simultaneously in Canada Illustration credits appear on page 272. Design and composition by Navta Associates, Inc. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600, or on the web at www.copy- right.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley.com/go/permissions. -

Subsidiaries and Associated Companies, in Which We Are Majority Or Minority Shareholders
Contents / Organizational chart / Milestones Companies Subsidiaries and associates We have a network of 46 subsidiaries and associated companies, in which we are majority or minority shareholders. During 2016, the molybdenum processing plant and the metal recovery plant, located in Mejillones, began operations. Codelco participates in companies and societies of several types, such as mining, developers of new uses of copper, research and technology, mineral processing plants, electric power, ports and healthcare entities. In addition are permanently, we seeking business opportunities in partnership with third parties, such as creating partnerships, acquisitions, mergers and sales. In 2016, Codelco made capital contributions to subsidiaries and associated companies for a total of US$ 150 million. In addition, the profits received by subsidiaries and associated companies amounted to US$ 78 million. Among the most relevant milestones of 2016 are the following: Mining Mineras • In the last quarter of the year, Molybdenum Processing Plant, of Investment Companies Inversión subsidiary Molyb Ltda., located in Mejillones, began operations. Electrical Rooms Eléctricas • Also, began operations the plant of Recuperadora de Metales SpA Processing plants subsidiary, located in Mejillones. Plantas de procesamiento New uses of copper • Santiago de Río Grande S.A. and CM Picacho societies were absorbed andNuevos molybdenum usos de cobre y molibdeno • Biosigma S.A. subsidiary changed its name to Codelco Tech SpA and Research &Investigación Technology absorbed IM2 S.A. y tecnología Trading companies • Codelco Canadá was created. Comercializadoras Port companies • 50% ownership in Copper Partners Ltda. was sold Portuarias Health and PensionsSalud y pensiones Companies 117 CODELCO 2016 ANNUAL REPORT Companies subsidiaries and associates Contents / Organizational chart / Milestones Agua de la Falda S.A.