Prospect Theory Based Portfolio Optimization Problem with Imprecise Forecasts
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Possibilities of Applying Markowitz Portfolio Theory on the Croatian Capital Market
POSSIBILITIES OF APPLYING MARKOWITZ PORTFOLIO THEORY ON THE CROATIAN CAPITAL MARKET Dubravka Pekanov Starčević, Ph.D. J. J. Strossmayer University of Osijek, Faculty of Economics in Osijek E-mail: [email protected] Ana ZRNIć, Ph.D. Student, J. J. Strossmayer University of Osijek, Faculty of Economics in Osijek E-mail: [email protected] Tamara Jakšić, BEcon, student J. J. Strossmayer University of Osijek, Faculty of Economics in Osijek E-mail: [email protected] POSSIBILITIES OF APPLYING MARKOWITZ PORTFOLIO THEORY ON THE CROATIAN CAPITAL... MARKOWITZ PORTFOLIO THEORY ON THE CROATIAN POSSIBILITIES OF APPLYING Abstract In order to achieve the maximum possible profit by taking the lowest possible risk, investors build a stock portfolio consisting of a specific number of stocks which, according to the principle of diversification, significantly reduce the risk of loss. To build a portfolio, in developed capital markets investors have used the Markowitz portfolio optimization model for many years that enables us to find an optimal risk-return trade-off by selecting certain stock combinations. Despite the development of the Zagreb Stock Exchange, i.e., the central trading venue in the Republic of Croatia, the Croatian capital market is still under- developed. It is characterized by numerous shortcomings such as low liquidity, lack of transparency, high stock price volatility and insufficient traffic. Accord- ingly, the aim of this paper is to provide an insight into the functioning of the Dubravka Pekanov Starčević • Ana Zrnić • Tamara Jakšić: Dubravka Pekanov Starčević • Ana Zrnić Tamara 520 Croatian capital market and to examine the possibility of building an optimal stock portfolio by using the Markowitz model. -

FIMA Daily Insight
FIMA Daily Insight IN FOCUS - ZAGREB STOCK EXCHANGE January 8, 2013 Stocks on ZSE traded higher today. CROBEX increased 0.24% to ZSE STOCK MARKET 1,808.40 pts while blue chip CROBEX10 gained 0.21% to 1,010.86 pts. CROBEX Last 1.808,4 Regular stock turnover amounted to HRK 14.4 million. % daily 0,24% Integrated telecom HT (HTRA CZ) topped the liquidity board collecting % YTD 3,91% HRK 4.3 million in turnover. The price increased 0.9% to HRK 210.70. CROBEX10 last 1010,9 Fertilizers producer Petrokemija (PTKMRA CZ) also came to focus again % daily 0,21% with HRK 1.5 million in turnover while price gained 5.5% to HRK 240.0. % YTD 4,05% Petrokemija was in investors’ focus few months ago, after speculations on Government selling its share of 1.7 million shares (50.6% of capital). Stock Turnov er (HRK m) 14,37 A few days ago Mladen Pejnović, head of the State Office for State Total MCAP (HRK bn) 194,39 Property Management confirmed government’s plans to privatize Source: w w w .zse.hr Petrokemija. Auto-parts producer AD Plastik (ADPLRA CZ) came to focus trading in -4,0% -2,0% 0,0% 2,0% 4,0% 6,0% blocks. The price advanced 1% to HRK 115.99 on HRK 1.3 million in PTKM-R-A ATPL-R-A turnover. AD Plastik currently trades at P/E=7.7, P/S=0.7 and DDJH-R-A P/Bv=0.7. VPIK-R-A LKPC-R-A Tobacco and tourism Adris group preferred share (ADRSPA CZ) was VIRO-R-A KORF-R-A also in investors’ focus with HRK 0.7 million in turnover while price KNZM-R-A slipped 1.3% to HRK 262.20. -

Raiffeisen Weekly Report, Nr. 38/2017
Raiffeisen Weekly Report Number 38 October 16th, 2017 Leaning on exports, the economy is growing Number of overnights stays On Tuesday the national statistical office delivered tourism figures for August (Jan – Aug) which showed expected growth of tourist arrivals and overnight stays (6.1%yoy 80 and 5.4%yoy respectively). The share of foreign tourists in the overnight stays 70 amounted 94.4%. Cumulatively, during the first eight months, the number of over- night stays was 72.5 million (+11.8% more than in the same period last year). 60 For the whole 2016 total number of overnight stays stood at 77.8mn. It is very mn 50 certain that, with data for September, this year will officially be a new record 40 tourist season. Although the strength of tourism helped Croatia remain on the 30 path of 3%yoy real growth, it also increased the sensitivity to potential downturns in tourism. As long as Croatia is perceived as a safe destination, it will retain its 20 attractive destination status. Under such circumstances, the budget picture will 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 look more favourable due to the stronger revenue inflow, especially VAT. Sources: CBS, Economic RESEARCH/RBA On the other side foreign trade activities in terms of import and export of goods remained subdued although the latest data pointed to a slight rise. In the period CPI, PPI, yoy from January to July, foreign trade deficit widened to EUR 4.9bn (+9.3%yoy). In 4 the same period, exports growth at 15.7%yoy compared to imports growth of 2 13.2%yoy resulted in coverage of imports by exports at 61.7% (+1.4pp). -

Market Commentary Portfolio Performance Vs Benchmark
Feb. FKHR1 Monthly Fund Update 2016 Market Commentary Following the publication of Q4 results, the share price jumped by 7.06% in one day. Viadukt operated with a net profit of HRK 3.2m in After a tumultuous start of the year, February brought on a reversal 2015, but this is still 36% less profit compared to the previous year. of trends in most of our largest holdings. This is in line with the rest Revenue fell by 9.1%, which is the consequence of an overall of European and global markets, which reached a bottom in mid- reduction in total investment in the Republic of Croatia, from which February, only to recover by the end of the month. The Croatian Viadukt achieves 99% of its total revenue. However, the growth in market started this recovery even sooner, having reached its lowest share price after the announcement of financial results might have point during January. However during February, the benchmark been due to the optimistic expectations for the rest of the year. The CROBEX index stayed mostly at the same level from the start of the construction industry expects a slight recovery and increased month, with only slight fluctuations. In the meantime, our fund investment from contracting authorities. managed to achieve a return of almost 4% MoM, beating the A third position that we want to emphasize is Đuro Đaković Holding market by a large margin. (ĐĐ). After having an amazing January, on the 15th and 19th of The most important contributor was our largest holding, the Adris February it was announced that Đuro Đaković signed contracts with Group, with common stock growing by over 10%. -

STOXX Sub Balkan 30 Last Updated: 01.05.2014
STOXX Sub Balkan 30 Last Updated: 01.05.2014 Rank Rank (PREVIOUS ISIN Sedol RIC Int.Key Company Name Country Currency Component FF Mcap (BEUR) (FINAL) ) SI0031102120 5157235 KRKG.LJ 515723 KRKA SI EUR Y 1.8 1 1 HRHT00RA0005 B288FC6 HT.ZA B288FC HRVATSKI TELEKOM HR HRK Y 0.8 2 2 SI0031102153 5272860 PETG.LJ 527286 PETROL D.D. SI EUR Y 0.5 3 3 SI0031104290 B0WTL89 TLSG.LJ B0WTL8 TELEKOM SLOVENIJE SI EUR Y 0.3 4 4 HRINA0RA0007 B1JMYF6 INA.ZA UC011 INA INDUSTRIJA NAFTE HR HRK Y 0.3 5 5 HRADRSPA0009 B1L6Z97 ADGR_p.ZA UC012 ADRIS GRUPA PREF HR HRK Y 0.2 6 6 RSNISHE79420 B51JZ61 NIIS.BEL RS101L NIS RS RSD Y 0.2 7 7 HRPODRRA0004 5053399 PODR.ZA UC005 PODRAVKA PREHRAMBENA IND. HR HRK Y 0.2 8 8 HRLEDORA0003 B28R4V5 LEDZ.ZA UC032 LEDO HR HRK Y 0.2 9 9 HRATGRRA0003 B29GN36 ATGR.ZA UC039 ATLANTIC GRUPA HR HRK Y 0.2 10 10 HRERNTRA0000 5303373 ERNT.ZA UC007 ERICSSON NIKOLA TESLA HR HRK Y 0.1 11 11 SI0031100082 5059621 MELR.LJ 505962 POSLOVNI SISTEM MERCATOR SI EUR Y 0.1 12 12 SI0021110513 B3B20Y9 POSR.LJ EN003 POZAVAROVALNICA SAVA SI EUR Y 0.1 13 14 HRKOEIRA0009 5371712 KONL.ZA UC006 KONCAR-ELEKTROINDUSTRIJA HR HRK Y 0.1 14 13 SI0031104076 7030721 GORE.LJ 703072 GORENJE VELENJE SI EUR Y 0.1 15 17 MKALKA101011 B3CDX19 ALK.MKE UY001 ALKALOID MK MKD Y 0.1 16 15 SI0031101346 5166640 LKPG.LJ 516664 LUKA KOPER SI EUR Y 0.1 17 16 SI0031103276 7030583 ARPO.LJ 703058 AERODROM LJUBLJANA SI EUR Y 0.1 18 19 HRKORFRA0007 7722341 DOMF.ZA UC009 VALAMAR ADRIA HOLDING HR HRK Y 0.1 19 18 RSAIKBE79302 B1LJDX6 AIKB.BEL US002 AIK BANKA RS RSD Y 0.1 20 22 MKKMBS101019 B2QVV96 KMB.MKE UY003 KOMERCIJALNA BANKA ORD. -

Mogućnosti Primjene Sintetičkih Pokazatelja U Predviđanju Bankrota Poduzeća Koja Kotiraju Na Zagrebačkoj Burzi
Mogućnosti primjene sintetičkih pokazatelja u predviđanju bankrota poduzeća koja kotiraju na Zagrebačkoj burzi Ćurković, Marko Professional thesis / Završni specijalistički 2020 Degree Grantor / Ustanova koja je dodijelila akademski / stručni stupanj: University of Zagreb, Faculty of Economics and Business / Sveučilište u Zagrebu, Ekonomski fakultet Permanent link / Trajna poveznica: https://urn.nsk.hr/urn:nbn:hr:148:875083 Rights / Prava: Attribution-NonCommercial-ShareAlike 3.0 Unported Download date / Datum preuzimanja: 2021-10-03 Repository / Repozitorij: REPEFZG - Digital Repository - Faculty of Economcs & Business Zagreb Marko Ćurković Matični broj studenta: PDS-6-2018 POSLIJEDIPLOMSKI SPECIJALISTIČKI RAD MOGUĆNOSTI PRIMJENE SINTETIČKIH POKAZATELJA U PREDVIĐANJU BANKROTA PODUZEĆA KOJA KOTIRAJU NA ZAGREBAČKOJ BURZI Poslijediplomski specijalistički studij „Računovodstvo i porezi“ Sveučilište u Zagrebu Ekonomski fakultet – Zagreb Mentor: prof. dr. sc. Ivana Mamić Sačer Zagreb, lipanj 2020. _____________________________ Ime i prezime studenta/ice IZJAVA O AKADEMSKOJ ČESTITOSTI Izjavljujem i svojim potpisom potvrđujem da je ____________________________________ (vrsta rada) isključivo rezultat mog vlastitog rada koji se temelji na mojim istraživanjima i oslanja se na objavljenu literaturu, a što pokazuju korištene bilješke i bibliografija. Izjavljujem da nijedan dio rada nije napisan na nedozvoljen način, odnosno da je prepisan iz necitiranog rada, te da nijedan dio rada ne krši bilo čija autorska prava. Izjavljujem, također, da nijedan -

CEE CIS Committee Decision
INDEX COMMITTEE DECISIONS Topic: CEE & CIS Index Committee Decisions From: Wiener Börse AG / Market & Product Development Date: March 18, 2009 All adjustments will be implemented after the close of the trading session on March 20, 2009 The Index Committee has decided upon the following adjustments: CTX, CECE, SCECE, CECE TR, CECExt effective March 23, 2009 New Number Name ISIN New FF New RF of Shares CEZ CZ0005112300 537.989.759 0,32 ERSTE BANK GROUP AT0000652011 0,90 TELEFONICA O2 CR CZ0009093209 0,97 Exclusion ZENTIVA NL0000405173 HTX, CECE, SCECE, CECE TR, CECExt effective March 23, 2009 New Number Name ISIN New FF New RF of Shares MAGYAR OLAJ GAZI HU0000068952 0,71 OTP BANK HU0000061726 0,95 RICHTER GEDEON HU0000067624 0,95 PTX, CECE, SCECE, CECE TR, CECExt effective March 23, 2009 New Number Name ISIN New FF New RF of Shares Exclusion AGORA PLAGORA00067 Inclusion ASSECO POLAND PLSOFTB00016 71.292.980 0,75 1,00 GETIN PLGSPR000014 710.930.354 TVN PLTVN0000017 169.159.984 SETX, CECExt effective March 23, 2009 New Number Name ISIN New FF New RF of Shares GORENJE SI0031104076 0,78 NOVA KREDITNA BKA. MARIBOR SI0021104052 0,78 PETROL SI0031102153 0,78 TELEKOM SLOVENIJE SI0031104290 0,78 Inclusion ADRIS GRUPA HRADRSPA0009 6.784.100 1,00 1,00 DALEKOVOD HRDLKVRA0006 0,50 KRKA SI0031102120 0,42 HRVATSKI TELEKOM HRHT00RA0005 0,73 Exclusion PRIVREDNA BANKA HRPBZ0RA0004 Page 1 of 5 NTX effective March 23, 2009 New Number Name ISIN New FF New RF of Shares ANDRITZ AT0000730007 0,99 Exclusion BANCA TRANSILVANIA ROTLVAACNOR1 ERSTE GROUP BANK AT0000652011 0,99 OMV AG AT0000743059 0,99 RAIFFEISEN INTERNATIONAL AT0000606306 0,99 Exclusion CENTRAL EUROP. -

Domestic Vs International Risk Diversification Possibilities in Southeastern Europe Stock Markets
Sinisa Bogdan, Suzana Baresa, and Zoran Ivanovic. 2016. Domestic vs International Risk Diversification Possibilities in Southeastern Europe Stock Markets. UTMS Journal of Economics 7 (2): 197–208. Preliminary communication (accepted August 27, 2016) DOMESTIC VS INTERNATIONAL RISK DIVERSIFICATION POSSIBILITIES IN SOUTHEASTERN EUROPEAN STOCK MARKETS Sinisa Bogdan Suzana Baresa Zoran Ivanovic1 Abstract Modern portfolio theory is one of the most important investment decision tools in finances. In 1952 Harry Markowitz set the foundations of the Modern portfolio theory, since than this theory was a backbone of many studies that dealt with investment decisions. This research applies mean-variance portfolio optimization on the international Southeastern Europe and domestic Croatian stock market exchange. Aim of this research is to compare risk diversification possibilities on the Southeastern European capital markets and on the Croatian Capital market. By analyzing nine stock market indices in the Southeastern Europe and twenty stocks from Zagreb Stock Exchange in the period of 36 months, results clearly show that internationally diversified portfolios offer better portfolio risk reduction than domestically diversified portfolios. Lowest achieved risk in international portfolio outperformed lowest achieved risk in domestic portfolio. Since risk is lower, returns are also much lower compared to domestic stock portfolios. Results of this research also report that domestic stock portfolios outperformed international portfolios at the risk level equal or higher than 0,97%, for the same risk, domestic portfolios offer greater returns. Keywords: Modern portfolio theory, portfolio optimization, stock portfolio, stock market indices, Zagreb stock exchange. Jel Classification: G11; C61 INTRODUCTION One of the investment theory assumptions is that investors should diversify their portfolios. -
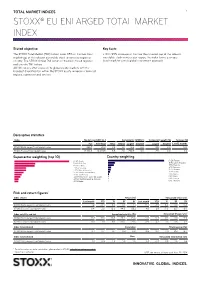
Stoxx® Eu Enlarged Total Market Index
TOTAL MARKET INDICES 1 STOXX® EU ENLARGED TOTAL MARKET INDEX Stated objective Key facts The STOXX Total Market (TMI) Indices cover 95% of the free-float » With 95% coverage of the free-float market cap of the relevant market cap of the relevant investable stock universe by region or investable stock universe per region, the index forms a unique country. The STOXX Global TMI serves as the basis for all regional benchmark for a truly global investment approach and country TMI indices. All TMI indices offer exposure to global equity markets with the broadest diversification within the STOXX equity universe in terms of regions, currencies and sectors. Descriptive statistics Index Market cap (USD bn.) Components (USD bn.) Component weight (%) Turnover (%) Full Free-float Mean Median Largest Smallest Largest Smallest Last 12 months STOXX EU Enlarged Total Market Index 266.7 121.0 0.6 0.1 10.3 0.0 8.5 0.0 N/A STOXX Europe Total Market Index 12,763.5 10,020.5 9.5 2.6 250.9 0.0 2.5 0.0 3.0 Supersector weighting (top 10) Country weighting Risk and return figures1 Index returns Return (%) Annualized return (%) Last month YTD 1Y 3Y 5Y Last month YTD 1Y 3Y 5Y STOXX EU Enlarged Total Market Index 1.2 -3.4 6.4 0.1 1.7 14.7 -4.9 6.3 0.0 0.3 STOXX Europe Total Market Index 0.4 2.0 18.3 44.5 55.2 4.8 2.9 17.9 12.7 8.9 Index volatility and risk Annualized volatility (%) Annualized Sharpe ratio2 STOXX EU Enlarged Total Market Index 15.1 15.0 16.3 23.2 25.3 -0.1 -0.4 0.4 0.0 -0.0 STOXX Europe Total Market Index 11.0 11.1 11.5 20.0 21.6 -0.9 0.3 1.3 0.6 0.4 Index to benchmark Correlation Tracking error (%) STOXX EU Enlarged Total Market Index 0.7 0.7 0.7 0.8 0.9 10.3 10.7 11.9 12.3 12.7 Index to benchmark Beta Annualized information ratio STOXX EU Enlarged Total Market Index 1.0 0.9 1.0 1.0 1.0 0.8 -0.8 -0.8 -1.0 -0.6 1 For information on data calculation, please refer to STOXX calculation reference guide. -

9Th - 11Th November 2014 Dubrovnik, Croatia
CENTRAL & SOUTHEAST EUROPEAN CONFERENCE OIL & GAS ARENA 2014 9th - 11th November 2014 Dubrovnik, Croatia www.infoarena.biz CENTRAL & SOUTHEAST EUROPEAN CONFERENCE Oil & Gas Arena 2014 9th - 11th November 2014, Dubrovnik, Croatia CENTRAL & SOUTHEAST EUROPEAN CONFERENCE Oil & Gas Arena 2014 9th - 11th November 2014, Dubrovnik, Croatia With recent developments in energy sector, Cen- tral-East and South-East Europe represent important region for the energy stability of European Union. Central-East Europe holds major oil and gas infra- structure and will stay in the future traditional cross- road for the European energy supply coming from the East. In the same time South-East Europe be- comes more and more important for the European energy sector in terms of alternative energy supply, but also in terms of new potential hydrocarbons re- serves and growth of their production in future. Both regions of Central-East and South-East Europe are also dominated with many small and medium sized national oil companies that play important role of their nation’s energy security. To fulfill this role, all these companies need to operate in a sustainable way and survive in today’s ever changing oil and gas industry. Therefore, many players and their state owners try to find answers for their future in strategic partnerships and joint ventures with bigger oil and gas players. But partnerships are not the only answer, companies also need to find ways to secure sustain- able operations by diversifying oil and gas supply for own market needs and by finding alternative streams of revenue. Central-East and South-East European Oil and Gas Arena 2014 will gather leading thought leaders from the oil and gas industry to show region’s perspective to the above trends with specific outlook for Croatia and neighboring countries. -

October 2017 FKHR1 Monthly Fund Update
October 2017 FKHR1 Monthly Fund Update Market Commentary While world stock exchanges reached record highs, primarily US Grupa and opened a bankruptcy procedure. After the ZSE decided stock market indexes, which are at the highest levels, the Croatian to remove the stock from its listings on 26th of October, the stock stock exchange index, CROBEX grew by 3.7% and is far from a soared by 68.43%. The stock ended the month trading at the all- significant recovery. US economy grew by 3% in the Q3 while time low since its listing. There is yet to see what is going to Amazon, Microsoft and Alphabet smashed forecasts and sent happen with this civil engineering firm, but the company NASDAQ to new record high. At the same time, the Fed did not announced in its annual report that their revenues fell by 82.3% raise its benchmark interest rate from its current 1% to 1.25% since last year. Also, the company said in a statement that they target, but indicated that one more hike is likely this year. Officials will sue Croatian government and that they will start the arbitrage also projected one rate hike less than initially forecasted between process because of the bridge Čiovo in Croatia. The government now and 2019. The World Bank held its assessment of the growth decided to break the contract with Viadukt d.d. for unknown of the Croatian economy this year at 2.9% and also said that risks reasons and employed an Austrian contractor. to the economy are moderate. The additional risks are posed by a still high level of indebtedness of the private sector, the Agrokor Hrvatski Telekom d.d. -

Annual Report on the Operation of the Strategic Companies And
2014. – ANNUAL REPORT ON THE OPERATIONS OF THE STRATEGIC COMPANIES AND COMPANIES OF SPECIAL INTEREST FOR THE REPUBLIC OF CROATIA 2014. - ANNUAL REPORT ON THE OPERATIONS 1 TABLE OF CONTENTS Page FOREWORD OF THE HEAD OF THE STATE ADMINISTRATIVE OFFICE FOR STATE PROPERTY MANAGEMENT ..................................................................................................................... 5 I. INTRODUCTION - DIVISION OF THE STATE PORTFOLIO - ACCORDING TO THE DECISION OF THE CROATIAN GOVERNMENT ON LAYING DOWN A LIST OF COMPANIES AND OTHER LEGAL ENTITIES OF STRATEGIC AND SPECIAL INTERESTS FOR THE REPUBLIC OF CROATIA ................................................................................ 7 II. PORTFOLIO OVERVIEW - 49 COMPANIES OF STRATEGIC AND SPECIAL INTEREST TO THE REPUBLIC OF CROATIA – ACCORDING TO ACTIVITIES .................................................................................................... 8 III. REVIEW OF OPERATIONS - 49 STRATEGIC AND COMPANIES OF SPECIAL INTEREST TO THE REPUBLIC OF CROATIA FROM 2011 TO 2014 ................................................................................................................. 9 III.I. TOTAL REVENUES, EXPENDITURES AND OPERATING RESULTS - 49 STRATEGIC AND COMPANIES OF SPECIAL INTEREST TO THE REPUBLIC OF CROATIA FROM 2011 TO 2014 .................................................... 11 III.II. NUMBER OF EMPLOYEES - 49 COMPANIES OF STRATEGIC AND SPECIAL INTEREST TO THE REPUBLIC OF CROATIA ON DECEMBER 31, 2014 FROM 2011 TO 2014 ...........................................................................