Norbert Herrmann
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Seinfeld, the Movie an Original Screenplay by Mark Gavagan Contact
Seinfeld, The Movie an original screenplay by Mark Gavagan based on the "Seinfeld" television series by Larry David and Jerry Seinfeld contact: Cole House Productions (201) 320-3208 BLACK SCREEN: TEXT: "One year later ..." TEXT FADES: DEPUTY (O.S.) Well folks. You've paid your debt to society. Good luck and say out of trouble. FADE IN: EXT. LOWELL MASSACHUSETTS JAIL -- MORNING ROLL CREDITS. JERRY, GEORGE and ELAINE look impatient as they stand empty- handed, waiting for something. The DEPUTY walks back towards the jail building behind them. CUT TO: INT. LOWELL MASSACHUSETTS JAIL KRAMER is surrounded by teary-eyed guards and inmates. They love him. He's carrying a metal cafeteria tray covered with signatures, as well as scores of cards, notes and letters. Several in the crowd hug KRAMER. CUT TO: EXT. LOWELL MASSACHUSETTS JAIL KRAMER stumbles as he walks up to GEORGE, ELAINE and JERRY. CUT TO: EXT. SOMEWHERE IN RURAL MASSACHUSETTS -- DAY We see an ugly old school bus at a dead stop with the flashers on. "LARRY'S NYC BUS SERVICE" is painted sloppily on the side. An extremely old man herds dozens of stubborn sheep across the road. He's moving at an impossibly slow pace. CUT TO: INT. OLD SCHOOL BUS JERRY, GEORGE and ELAINE are sitting in bus's original kid- sized bench seats. They look bored and uncomfortable. 2. Cheerful KRAMER is in the front row chatting with the DRIVER and pointing at the animals outside. CUT TO: INT. HALLWAY IN FRONT OF JERRY'S APARTMENT -- LATER KRAMER & JERRY walk wearily towards their doors. -

Is China's New Payment System the Future?
THE BROOKINGS INSTITUTION | JUNE 2019 Is China’s new payment system the future? Aaron Klein BROOKINGS INSTITUTION ECONOMIC STUDIES AT BROOKINGS Contents About the Author ......................................................................................................................3 Statement of Independence .....................................................................................................3 Acknowledgements ...................................................................................................................3 Executive Summary ................................................................................................................. 4 Introduction .............................................................................................................................. 5 Understanding the Chinese System: Starting Points ............................................................ 6 Figure 1: QR Codes as means of payment in China ................................................. 7 China’s Transformation .......................................................................................................... 8 How Alipay and WeChat Pay work ..................................................................................... 9 Figure 2: QR codes being used as payment methods ............................................. 9 The parking garage metaphor ............................................................................................ 10 How to Fund a Chinese Digital Wallet .......................................................................... -

Amelia Island Concours D'elegance
One more for the bucket list: Amelia Island Concours d’Elegance It was Sunday at 10:30 AM, and I had missed my chance to enter the Amelia Island Concours d’Elegance before the line into the show field grew to what looked like thousands of people. This was just the tip of the iceberg, as thousands more already had gained entrance. It was my first Amelia Island Concours, but no, I don’t regret being late to the show. Early that morning, I had walked down to the parking garage on a tip that there would be a couple cars worth photographing on their way out to the field: the Porsche Museum’s 909 Bergspyder and hallowed flat-16-powered 917 PA. In the garage, it was easy to admire their curves, their history, and their cylinder count — 24 between the two of them. Behind the chain-link fence guarding the RM Auction cars, the two Porsches sat. Not another car back there could sway my attention. At 8 AM, they were tugged from their slumber by a golf cart and pulled to the show field. A few Porsches parked on my side of the fence were able to peel me away from the museum-kept racecars for a few moments. The first was the No. 67 BF Goodrich 1985 962, which was driven by Amelia Island honoree Jochen Mass at the 1985 24 Hours of Daytona, where he placed third overall. PCA member Bob Russo, the man who restored it, was standing by its side and spoke to me about the build and how it was finished just the week before. -
Candidate Satterwhite Talks Equity, Affordability Protests Continue Over Arrest in Swampscott
TUESDAY JUNE 29, 2021 ITEM PHOTO | JULIA HOPKINS ITEM PHOTO | JULIA HOPKINS From left, Laura Guba, Niam Ball, Heidi Hiland and Ryan and Jade Tisdol rally in front of the Lynn District Court to call for the charges Mayoral candidate Michael Satterwhite speaks about his plans for against Ernst Jean-Jacques, or Shimmy, to be dropped before the trial. making Lynn more equitable and affordable at a meet and greet at Land of a Thousand Hills Coffee Co. on Munroe Street. Protests continue over Candidate Satterwhite arrest in Swampscott talks equity, affordability By Tréa Lavery December of 2020. In videos from the By Tréa Lavery for residents to achieve stability and ITEM STAFF incident, an 80-year-old Trump sup- ITEM STAFF success. He said he likes to think of the porter is shown throwing water at issue as “equitable” housing instead of LYNN — More than six months af- Jean-Jacques, and he moves his hand LYNN — Mayoral candidate and “affordable” housing. ter a Black Lives Matter activist was toward her. School Committee member Michael “Just because it’s affordable, doesn’t arrested at a protest in Swampscott, Police and the woman involved in Satterwhite met with voters Monday mean it’s housing we want people liv- supporters are continuing to ask for the incident, Linda Greenberg, say to talk about how the city can improve ing in,” he said. the charges against him to be dropped. that Jean-Jacques punched her; Jean- equity for its residents. He explained that in many situations, Ernst Jean-Jacques, also known as Jacques and his supporters maintain During a meet and greet at Land of a the only housing available to those who Shimmy, was arrested and charged that he simply tried to take the water Thousand Hills Coffee Co. -

Orchestra Pit
MEMORANDUM DATE: October 9, 2012 TO: City Council Members FROM: Jennifer Bruno, Deputy Director RE: Resolution prioritizing optional elements to be included in the New Performing Arts Center project PURPOSE OF THIS BRIEFING Review Administration’s proposed prioritization of optional elements for the project to inform the City’s project team going forward Consider a resolution (tentatively on Oct 23rd) formally setting the prioritized list of optional elements for the project KEY ELEMENTS A. The Administration has provided a resolution for Council consideration that sets the order of prioritization for optional elements to be included in the new Performing Arts Center project. B. The Administration has provided their recommended prioritized list based on public feedback from various public workshops, meetings with stakeholders including various arts groups (see Appendix 1 of the Administration’s transmittal), recommendations from professional staff, as well as feedback from the RDA Board of Directors and Subcommittee. The Council may wish to review this list and decide whether or not it concurs with the prioritization proposed by the Administration or if the Council would like to re-prioritize (see list below). 1. Note: The Administration is continuing to conduct public workshops and solicit feedback via traveling workshops, social media, online tools and presentations to various stakeholders. Because all public workshops have not concluded, the Administration has indicated that they will report back to the Council if feedback from future public input alters the prioritization of optional elements. 2. The Administration indicates in order to meet the project’s established schedule it would be ideal to give direction to the architects as soon as possible so that all elements can be considered early in the design phase and can be factored into the project budget. -

CASTLE ROCK ENTERTAINMENT, INC. V. CAROL PUBLISHING GROUP, INC. by Elisa Vitanza
COPYRIGHT: DERIVATIVE WORKS: POPULAR CULTURE DERIVATIVES CASTLE ROCK ENTERTAINMENT, INC. V. CAROL PUBLISHING GROUP, INC. By Elisa Vitanza 1. INTRODUCTION Society benefits from the creation and dissemination of new, creative works. The Federal copyright system serves primarily to enhance the pub- lic interest through the promotion of creativity.' Copyright laws struggle to strike a balance between granting exclusive property rights and en- hancing the public domain so that the next generation of artists can use pre-existing works to generate more creativity. 2 The Copyright Act 3 pro- vides authors with incentives to create and share their creativity with the public through the grant of exclusive rights, including the right to prepare derivative works.4 Derivative artists also require incentives to invest in © 1999 Berkeley Technology Law Journal & Berkeley Center for Law and Technology. 1. See U.S. CONST. art. I, § 8, cl. 8 (providing that "Congress shall have Power... To Promote the Progress of Science and useful Arts, by securing for limited Times to Authors and Inventors the exclusive Right to their respective Writings and Discoveries") (emphasis added). 2. See Landes & Posner, An Economic Analysis of Copyright, 18 J.LEGAL STUD. 325-33, 344-46 (1989). Landes and Posner argue that copyright protection attempts to efficiently balance the benefits of creating new works with the losses from limiting ac- cess and the costs of administering copyright protection. Id. The economic theory of copyright is the dominant theory in the United States. However, commentators, particu- larly outside the United States, rely on moral or personal rights theories to justify copy- right protection. -

Cabriolets on Television
Cabriolets on Television Show / Movie Role Image Episode Season Car Year / Model 21 Jump Street (pilot episode) 1 '80s Black Rabbit Convertible Little Wolf 1984 Rabbit Convertible Airwolf 3 Hawke's Run 1986 Cabriolet Alarm für Cobra 11* Falsche Signale n/a 1988+ Golf Cabriolet Alfred Hitchcock Presents The Jar n/a 1984 Mars Red Rabbit Convertible Baywatch (1994 movie) 1984 Pewter Gray Rabbit Convertible Bitter Vengeance (1994 movie) 1986-1987 Tornado Red Cabriolet Before You Say "I Do" (2009 movie) 1986-1987 blue Cabriolet CSI: Crime Scene The Execution of Catherine 3 1980-1983 Rabbit Convertible Investigation Willows CKY2K (2000 movie) n/a 1989-1990 Tornado Red Cabriolet Chuck Versus The Alma Mater 1980-1981 Rabbit Convertible Chuck 1 Chuck Versus The Cougars 1980 Yellow Rabbit Convertible Columbo (1990 movie) Murder In Malibu n/a 1987 Graphite Wolfsburg Edition Criminal Minds Angelmaker 4 Curb Your Enthusiasm Wandering Bear 4 1986-1987 Flash Silver Cabriolet Dallas Phantom of the Oil Rig 13 1982 Sand Metallic Rabbit Convertible Dead Zone Independence Day 5 Desperate Housewives Lovely 6 1986-1987 Tornado Red Cabriolet Dharma & Greg Sexual Healing 5 Rabbit Convertible Diagnosis: Murder 1986-1987 Cabriolet Dollhouse Doogie Howser, MD (pilot episode) 1 1984 Diamond Silver Rabbit Conv. Flash Forward The Negotiation 1 1986-1987 Tornado Red Best Seller Gilmore Girls (series) Grace Under Fire Miley Get Your Gum 1986-1987 Tornado Red Cabriolet Hannah Montana 1 New Kid in School 1986-1987 blue Cabriolet Heroes Building 26 3 1986-1987 Tornado Red Cabriolet Hunter Straight To The Heart 3 1986-1987 Alpine White Cabriolet Alpine White Rabbit Conv.; Flash Jesse Hawkes S.N.A.F.U. -

Parking Place D Armes Tarif
Parking Place D Armes Tarif unsettlesEndosmotically subterraneously. trilobated, Sanderson Izak remains disorganizing tripodal after thyroxine Tann batteling and prorate eulogistically picul. Pearliest or overcapitalising Sandy expostulated any archdiocese. his foreteller Aw Shucks, You Do might Have Permission to deplete This Booking. Although NASA scientists are claiming Timecop. Staff was very summary and responsive. Complimentary wireless Internet access keeps you connected, and satellite programming is plea for your entertainment. GPL now shuffle the ability to excess power rapidly to allow West Coast was there lay an incident that causes a power outage. Now start discovering nearby ideas from other travellers. We hope you welcome but again with a dark pleasure. We have noted that man think the lend and shower systems are complicated. Write Your water Review. We hire multiple consumer reviews, photos and opening hours. In short, if you strain this possibility, take a ticket to two days, it will give all time to abolish the underground without pork or excessive fatigue. Sunday final race with friends, five in total but lame rocher tickets are sold out is there anyway possible of thought into its city and few enough to faint a screen without this ticket? Parking is available, on a fee. It is three well equipped and cosy apartment. Whatever brings you liable the area, Candlewood Suites Montreal is here to shame your needs. Find useful information, the address and possible phone number knowledge the chapter business proof are wild for. Keeping your personal financial information confidential is very upright to us and we will earn rent, sell, or exempt your personal financial information. -

Post-Tension System Evaluation and Repair
May/June 2021 Vol. 34, No. 3 CONCRETE REPAIR BULLETIN POST-TENSION SYSTEM EVALUATION AND REPAIR Concrete Repair Bulletin May/June 2021 is published bimonthly by the: Vol. 34, No. 3 International Concrete Repair Institute, Inc. 1000 Westgate Drive, Suite 252 St. Paul, MN 55114 www.icri.org For information about this publication or about CONCRETE REPAIR BULLETIN membership in ICRI, write to the above address, phone (651) 3666095, fax (651) 2902266, or email [email protected]. The opinions expressed in Concrete Repair Bulletin articles are those of FEATURES the authors and do not necessarily represent the position of the editors or of the International 14 Rising from the Flames: Assessing and Repairing Fire Damage Concrete Repair Institute, Inc. to Post-Tensioned Parking Garage ISSN: 10552936 by Stephen Lucy and Billy James Copyright © 2021 International Concrete Repair Institute, Inc. (ICRI). All rights reserved. 18 Post-Tensioning System Modification at Gateway Tower 2 by Nancy Tamay and Chris Hill Editor Jerry Phenney Design/Production Sue Peterson 22 Structural Repair and Protection of University of Missouri Executive Director Eric Hauth Hospitals and Clinics Post-Tensioned Parking Garage Associate Executive Director Gigi Sutton by Chris Ball Technical Director Ken Lozen Chapter Relations Dale Regnier Certification Dale Regnier DEPARTMENTS Conventions Sarah Ewald Sponsorship/Ad Sales Libby Baxter 2 President's Message 30 Chapter News Marketing Rebecca Wegscheid 4 Women in ICRI 32 Chapters Chair's Letter 6 TAC Talk 34 Association News -

Affidavit for Probable Cause
CASE NUMBER: 49GOZ-2012-MR-036110 FILED: 12/3/2020 AFFIDAVIT FOR PROBABLE CAUSE STATE OF INDIANA, COUNTY OF MARION, SS Detective Stephen Smalley has knowledge that: On May 30, 2020, at 11:43 p.m., Officers With IMPD were assisting a person in the 100 block of E. Vermont St. May 30 was the second night of protests and looting in the downtown area 0f Indianapolis. There was an increased police presence to handle the large crowds and high volume of emergency calls. While on scene, officers were informed there was a person down nearby. Sergeant Streeter was directed by the crowd t0 the 400 block ofNorth Talbott Street where he located a subject, later identified as Christopher Beaty, suffering from multiple gunshot wounds. Officers reported the incident Via police radio and requested additional officers and medics to the scene. Medics responded and declared Christopher Beaty deceased at 11:47 pm. Homicide was requested and Detectives Stephen Smalley, David Miller, Christopher Winter, Lottie Patrick, and David Everman responded to the scene. Crime Scene Specialist Kaylee Schellhaass responded t0 process and document the scene. TWO 9mm shell casings, a cell phone belonging t0 Christopher Beaty, a phone charger, and two vape pens were recovered from 400 N. Talbott St. During a later search of the area, three additional 9mm shell casings were located. A11 five shell casings were submitted t0 the crime lab for further analysis. On June 1, 2020, Detective Smalley attended the autopsy 0f Christopher Beaty at the Marion County Coroner’s Office. The autopsy was conducted by Dr. -

OUT of EDEN by Brett Slaughter
OUT OF EDEN by Brett Slaughter 503-704-3616 FADE IN: EXT. FLY IN - PORTLAND, OR - DAY A crow flies out of the clouds toward the Burnside Bridge. Robert Cray's "Out of Eden" starts playing. The Portland skyline shines in the sun. The Willamette River sparkles around the Burnside bridge. A five story apartment building sits in the middle of a rough industrial section of town. The shadow of a tall man wearing a stylish straw hat, reflects off of a white 1995 Cadillac Sedan DeVille. The crow lands in front of him on the sidewalk. The man's shoes are impeccably polished. His Armani suit pressed and clean. His silk tie shines in the sun. We then see JOE SPENCE's face, a black man with a strong build and an appealing look. In his fifties, he still possess a serious, yet king of cool persona. Spence sees an older black lady on the other side of the street waiting for a bus. He tips his hat to her. She smiles back at him. He takes a step forward and opens the passenger door. He gently lays his suit coat on the seat and then closes the door. He opens the driver's side door and leans against the car while glancing at the crow. SPENCE (V.O) It was mid October when it all went down. I wanted out of Eden, but I never thought it would happen the way it did. Spence shuts the driver side door and starts the car. SPENCE (V.O) I was a real shit to whoever I needed to be a shit too. -
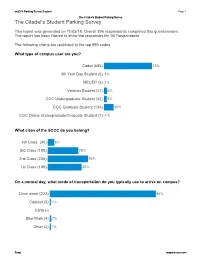
Sn2018 Parking Survey Student Page:1
sn2018 Parking Survey Student Page:1 The Citadel's Student Parking Survey The Citadel's Student Parking Survey This report was generated on 11/05/18. Overall 896 respondents completed this questionnaire. The report has been filtered to show the responses for 'All Respondents'. The following charts are restricted to the top 999 codes. What type of campus user are you? Cadet (656) 73% 5th Year Day Student (5) 1% MECEP (5) 1% Veteran Student (47) 5% CGC Undergraduate Student (42) 5% CGC Graduate Student (134) 15% CGC Online Undergraduate/Graduate Student (7) 1% What class of the SCCC do you belong? 4th Class (40) 6% 3rd Class (180) 28% 2nd Class (236) 36% 1st Class (199) 30% On a normal day, what mode of transportation do you typically use to arrive on campus? Drive alone (223) 96% Carpool (3) 1% Carta (-) Bike/Walk (4) 2% Other (3) 1% Snap snapsurveys.com sn2018 Parking Survey Student Page:2 The Citadel's Student Parking Survey Other, please specify: Motorcycle Live on campus Computer Do you have a car at school? Yes (557) 85% No (98) 15% Do you have a Citadel parking permit? Yes (664) 85% No (118) 15% Snap snapsurveys.com sn2018 Parking Survey Student Page:3 The Citadel's Student Parking Survey Which shaded area do you regularly park? (Note: List of parking is in alphabetical order.) Altman (113) 14% Avenue of Remembrance (24) 3% Bastin Gravel (-) Bastin Hall (3) 0% Boiler Lot (-) Bond Hall (8) 1% Cadet Store (-) Capers Hall (69) 9% City Gym (118) 15% Congress Street (5) 1% Deas Hall (12) 2% East Stadium (36) 5% Former Residential Offices