DOCSLIB.ORG

ACER Research Conference Proceedings (2010)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
ACER Research Conference Proceedings (2010) Conference Proceedings Contents Foreword v Keynotepapers Professor David Clarke 3 Speaking in and about mathematics classrooms internationally: The technical vocabulary of students and teachers. Mr Phil Daro 8 Standards, what’s the difference?: A view from inside the development of the Common Core State Standards in the occasionally United States. Professor Kaye Stacey 17 Mathematics teaching and learning to reach beyond the basics. Professor Paul Ernest 21 The social outcomes of school mathematics: Standard, unintended or visionary? Concurrentpapers Professor Robyn Jorgenson 27 Issues of social equity in access and success in mathematics learning for Indigenous students. Professor Tom Lowrie 31 Primary students’ decoding mathematics tasks: The role of spatial reasoning. Professor John Pegg 35 Promoting the acquisition of higher order skills and understandings in primary and secondary mathematics. Associate Professor Rosemary Callingham 39 Mathematics assessment in primary classrooms: Making it count. Dr David Leigh-Lancaster 43 The case of technology in senior secondary mathematics: Curriculum and assessment congruence? Associate Professor Joanne Mulligan 47 Reconceptualising early mathematics learning. Professor Peter Sullivan 53 Learning about selecting classroom tasks and structuring mathematics lessons from students. Mr Ross Turner 56 Identifying cognitive processes important to mathematics learning but often overlooked. Associate Professor Robert Reeve 62 Using mental representations of space when words are unavailable: Studies of enumeration and arithmetic in Indigenous Australia. Professor Merrilyn Goos 67 Using technology to support effective mathematics teaching and learning: What counts? Dr Shelley Dole 71 Making connections to the big ideas in mathematics: Promoting proportional reasoning. Dr Sue Thomson 75 Mathematics learning: What TIMSS and PISA can tell us about what counts for all Australian students. Posterpresentations 81 Conferenceprogram 85 CrownConferenceCentremapandfloorplan 89 Conferencedelegates 93 Research Conference 2010 Planning Committee Professor Geoff Masters CEO, Conference Convenor, ACER Dr John Ainley Deputy CEO and Research Director National and International Surveys, ACER Professor Kaye Stacey Professor Mathematics Education, University of Melbourne Dr David Leigh-Lancaster Mathematics Manager, Victorian Curriculum and Assessment Authority Mr Ross Turner Principal Research Fellow, ACER Ms Kerry-Anne Hoad Director ACER Institute, ACER Ms Lynda Rosman Manager Programs and Projects, ACER Institute, ACER Copyright © 2010 Australian Council for Educational Research 19 Prospect Hill Road Camberwell VIC 3124 AUSTRALIA www.acer.edu.au ISBN 978-0-86431-958-6 Design and layout by Stacey Zass of Page 12 and ACER Project Publishing Editing by Carolyn Glascodine and Kerry-Anne Hoad Printed by Print Impressions Research Conference 2010 iv Foreword GeoffMasters Australian Council for Educational Research Research Conference 2010 is the fifteenth national Research Conference. Through our research conferences, ACER provides significant opportunities at the national Geoff Masters is Chief Executive Officer and a level for reviewing current research-based knowledge in key areas of educational member of the Board of the Australian Council policy and practice. A primary goal of these conferences is to inform educational for Educational Research (ACER) – roles he has policy and practice. held since 1998. He has a PhD in educational measurement from Research Conference 2010 brings together key researchers, policy makers and the University of Chicago and has published teachers from a broad range of educational contexts from around Australia and widely in the fields of educational assessment and overseas. The conference will explore the important theme of teaching and learning research. mathematics. The conference will draw together research-based knowledge about Professor Masters has served on a range of effective teaching and learning of mathematics and explore approaches to teaching bodies, including terms as founding President of that develop the mathematical proficiency of students and catch their interest in the Asia-Pacific Educational Research Association; President of the Australian College of Educators; mathematics from the early years through to post-compulsory education. Chair of the Technical Advisory Committee for We are sure that the papers and discussions from this research conference will the International Association for the Evaluation of Educational Achievement (IEA); Chair of make a major contribution to the national and international literature and debate on the Technical Advisory Group for the OECD’s key issues related to the effective teaching and learning of mathematics. Programme for International Student Assessment (PISA); member of the Business Council of We welcome you to Research Conference 2010, and encourage you to engage Australia’s Education, Skills and Innovation in conversation with other participants, and to reflect on the research and its Taskforce; member of the Australian National connections to policy and practice. Commission for UNESCO (and Chair of the Commission’s Education Network); and member of the International Baccalaureate Research Committee. He has undertaken a number of reviews for governments, including a review of examination procedures in the New South Wales Higher School Certificate (2002); an investigation of options for the introduction of an Australian Certificate of Education (2005); a national review Professor Geoff N Masters of options for reporting and comparing school Chief Executive Officer, ACER performances (2008); and a review of strategies for improving literacy, numeracy and science learning in Queensland primary schools (2009). Professor Masters was the recipient of the Australian College of Educators’ 2009 College Medal in recognition of his contributions to education. vii Research Conference 2010 viii Keynote papers Speaking in and about mathematics classrooms internationally: The technical vocabulary of students and teachers Abstract Presentation summary This presentation takes patterns of Classroom discourse (and professional language use as the entry point for discourse about classrooms) is a form the consideration of discourses in and of social performance undertaken about the mathematics classroom. within affordances and constraints These patterns of language take the that can be both cultural and linguistic. form of discourses performed within The nature of these discourses, as mathematics classrooms around the performed in mathematics classrooms, world and among the international provides a key indicator of pedagogical DavidClarke mathematics education community principles underlying classroom practice University of Melbourne about the mathematics classroom. and the theories of learning on which Cross-cultural comparisons reveal these principles are implicitly founded. David Clarke is a Professor of Education and how discourses in and about the The discourses about mathematics the Director of the International Centre for Classroom Research (ICCR) at the University mathematics classroom have developed classrooms give expression to these of Melbourne. Over the last 15 years, Professor in different cultures. Research is used pedagogical principles sometimes Clarke’s research activity has centred on capturing to explore the role of spoken language explicitly and sometimes through the complexity of classroom practice through a in mathematics classrooms situated embedding privileged forms of program of international video-based classroom research. The ICCR is unique in the facilities in Asian and Western countries. In practice in the naming conventions by it offers for the manipulation and analysis of conceptualising effective learning, which the mathematics classroom is classroom data and provides the focus for researchers, teachers and curriculum described. From research undertaken in collaborative activities among researchers from developers need to locate proficiency classrooms situated in different cultures, China, the Czech Republic, Germany, Hong Kong, Israel, Japan, Korea, New Zealand, Norway, the with mathematical language within it appears that both mathematical Philippines, Portugal, Singapore, South Africa, their framework of valued learning discourse and professional discourse Sweden, the United Kingdom and the United outcomes. Further, different cultures, take different forms and are differently States of America. Under Professor Clarke’s employing different languages, have valued in different communities. This direction the ICCR has developed a system for web-mediated, secure, high-speed data chosen to name and therefore privilege presentation draws on and connects entry, retrieval and analysis on an international different classroom activities. Research research into these two discourses. scale (videoPortal). Other significant research is reported into how language is has addressed teacher professional learning, and might be used to describe the The spoken metacognition, problem-based learning, and events of mathematics classrooms assessment (particularly the use of open- mathematics study ended tasks for assessment and instruction in in different cultures. Research and mathematics). Current research activities involve theorising undertaken in and about Research was conducted into the multi-theoretic research designs, cross-cultural those mathematics classrooms must situated use of mathematical language analyses and the
Load more

Recommended publications
  • Student Exchanges
    Student Exchanges Introduction ................................................................................................................................................................... 2 Rationale ....................................................................................................................................................................... 2 How Do Students Qualify and Apply ........................................................................................................................... 3 Student Profile Sheet .................................................................................................................................................... 4 Section A .................................................................................................................................................................. 5 Section B .................................................................................................................................................................. 6 Rules for Exchanges ................................................................................................................................................... 10 Information for Outgoing Exchange Students ............................................................................................................ 16 Academic Issues ......................................................................................................................................................... 17 Exchange
    [Show full text]
  • 31/08/2018 1 of 8 ROSTRUM VOICE of YOUTH NATIONAL FINALISTS
    ROSTRUM VOICE OF YOUTH NATIONAL FINALISTS Year Nat Final Convenor Zone Coordinator Junior Finalist School Place Senior Finalist School Place National Coordinator 1975 Tom Trebilco ACT Tom Trebilco Fiona Tilley Belconnen HS 1 Linzi Jones 1975 NSW 1975 QLD Vince McHugh Sue Stevens St Monica's College Cairns Michelle Barker 1975 SA NA NA NA Sheryn Pitman Methodist Ladies College 2 1975 TAS Mac Blackwood Anthony Ackroyd St Virgils College, Hobart 1 1975 VIC 1975 WA Year Nat Final Convenor Zone Coordinator Junior Finalist School Place Senior Finalist School Place 1976 Tom Trebilco? ACT Tom Trebilco? Tim Hayden Telopea Park HS 1 (tie) 1976 NSW 1976 QLD Vince McHugh Michelle Morgan Brigadine Convent Margaret Paton All Hallows School Brisbane 1976 SA NA NA NA NA NA 1976 TAS Mac Blackwood Lisa Thompson Oakburn College 1 (tie) 1976 VIC 1976 WA Paul Donovan St Louis School 1 Year Nat Final Convenor Zone Coordinator Junior Finalist School Place Senior Finalist School Place 1977 ACT Michelle Regan (sub) Belconnen HS 1977 NSW John White Kerrie Mengerson Coonabarabran HS 1 Sonia Anderson Francis Greenway HS,Maitland 1 1977 QLD Mervyn Green Susan Burrows St Margarets Clayfield Anne Frawley Rockhampton 1977 SA NA NA NA NA NA 1977 TAS Mac Blackwood Julie Smith Burnie High Gabrielle Bennett Launceston 1977 Richard Smillie VIC Pat Taylor Linda Holland St Anne's Warrnambool 3 Kelvin Bicknell Echuca Technical 1977 WA David Johnston Mark Donovan John XX111 College 2 Fiona Gauntlett John XX111 College 2 Year Nat Final Convenor Zone Coordinator Junior Finalist
    [Show full text]
  • Girls Representative Volleyball Team Associated
    GIRLS REPRESENTATIVE VOLLEYBALL TEAM v ASSOCIATED PUBLIC SCHOOLS Tuesday, 30 March 2021 at 12:30 p.m. Haileybury (Gym 2) 855-891 Springvale Road, Keysborough NO: FIRST NAME AND SURNAME SCHOOL 10 Adrienne Battistella Ivanhoe Grammar 7 Rebekah Konstantopoulos Ivanhoe Grammar 6 Chloe Jacobi (Co-Captain) Ivanhoe Grammar 11 Ana Gakovic Peninsula Grammar 16 Victoria Day Penleigh and Essendon Grammar 9 Charlee Kemp Penleigh and Essendon Grammar 5 Alannah Boell Yarra Valley Grammar School 2 Lauren Dickins Yarra Valley Grammar School 8 Molly Heymanson (Co-Captain) Yarra Valley Grammar School 4 Ruby Nicks Yarra Valley Grammar School Coach: Steve Holder (Yarra Valley Grammar) Final Scores AGSV: 3 def APS: 1 25-16, 26-24, 22-25, 25-20 Associated Grammar Schools of Victoria GIRLS REPRESENTATIVE VOLLEYBALL TEAM The AGSV v APS Girls Representative Volleyball match scheduled for Tuesday, 24 March 2020 at 12:30 p.m. at Haileybury (Keysborough) was cancelled due to the Coronavirus (COVID-19) pandemic. NO: FIRST NAME AND SURNAME SCHOOL Chloe Jacobi Ivanhoe Grammar Victoria Day Penleigh & Essendon Grammar Georgie Simmons Penleigh & Essendon Grammar Emily Davis Peninsula Grammar Jenna Lamb Peninsula Grammar Alannah Boell Yarra Valley Grammar Lauren Dickins Yarra Valley Grammar Molly Heymanson Yarra Valley Grammar Ruby Nicks Yarra Valley Grammar EMERGENCIES (order of listing is irrelevant) Ana Gakovic Peninsula Grammar Livinia Stockdale Mentone Grammar Lucia Taitoko Mentone Grammar Coach: Olivia Phillips / Steve Holder (Yarra Valley Grammar) Associated Grammar
    [Show full text]
  • Download Brochure
    PARKSIDE RESIDENCES BOX HILL, MELBOURNE A COLLECTION OF PREMIUM RESIDENCES ARCHITECTURE LOCATION A PLACE TO FLOURISH 11 51 A PLACE TO FLOURISH APARTMENTS TEAM 31 63 4 CONTENTS 5 Irving Domain is your place to flourish. INTRODUCTION A PLACE TO FLOURISH A PLACE TO FLOURISH “We strive to create buildings that Ensconced in a tranquil, parkside locale, in the heart of Box Hill’s sit honestly within their context and, CBD, the residents at Irving Domain will have it all. The thirteen level building features a broad selection of 1, 2 and 3 bedroom make a generous contribution to apartments, defined by craftsmanship and innovative function. the community. The most important consideration is how each space DKO Architecture is a widely recognised and awarded design practice. The architecture and interior design at Irving Domain will make its occupant feel. At Irving is understated and elegant, inspired by an environment where Domain, the design develops effortless city-living coexists with nature. The building makes a conscious connections with nature and a yet unassuming contribution to its parkside surrounds, while sophisticated sense of home.” interiors feature authentic and uncomplicated materials, applied with a bold approach that mixes scale and texture. JESSE LINARDI, DESIGN DIRECTOR, Large, private outdoor spaces are just one of the unexpected DKO ARCHITECTURE. inclusions that reference the fundamentals of a traditional house, delivered in the format of a high-end modern apartment. Atop the building, a shared rooftop retreat brings residents together in lively social spaces to cook, dine, entertain and relax. Across lower ground levels, ample parking for cars and bicycles is enhanced by security and easy accessibility.
    [Show full text]
  • An Examination of Trinity Grammar School, Sydney, 1913 to 1976
    University of Wollongong Research Online University of Wollongong Thesis Collection 1954-2016 University of Wollongong Thesis Collections 1989 An evangelical school in an evangelical diocese: an examination of Trinity Grammar School, Sydney, 1913 to 1976 Phillip J. Heath University of Wollongong Follow this and additional works at: https://ro.uow.edu.au/theses University of Wollongong Copyright Warning You may print or download ONE copy of this document for the purpose of your own research or study. The University does not authorise you to copy, communicate or otherwise make available electronically to any other person any copyright material contained on this site. You are reminded of the following: This work is copyright. Apart from any use permitted under the Copyright Act 1968, no part of this work may be reproduced by any process, nor may any other exclusive right be exercised, without the permission of the author. Copyright owners are entitled to take legal action against persons who infringe their copyright. A reproduction of material that is protected by copyright may be a copyright infringement. A court may impose penalties and award damages in relation to offences and infringements relating to copyright material. Higher penalties may apply, and higher damages may be awarded, for offences and infringements involving the conversion of material into digital or electronic form. Unless otherwise indicated, the views expressed in this thesis are those of the author and do not necessarily represent the views of the University of Wollongong. Recommended Citation Heath, Phillip J., An evangelical school in an evangelical diocese: an examination of Trinity Grammar School, Sydney, 1913 to 1976, Master of Arts (Hons.) thesis, Faculty of Education, University of Wollongong, 1989.
    [Show full text]
  • Our Loreto Values
    Online Information BAS Website The BAS Website (www.bas.vic.edu.au ) is a useful tool in accessing results, draws, ladders, and venue locations. Once on the homepage, click on ‘Sport’ and then the drop down ‘Results’ option. From here you can select the appropriate sport (and grade if applicable). E-Newsletter As part of the Loreto College Ballarat E-Newsletter, there will be regular updates on the progress of our sporting teams throughout each term, along with any other news and events. Our Loreto Values Freedom ‘It is an inner freedom, accepting of self, open to others and trusting of life.’ Justice ‘To recognise the inherent dignity of each individual and of the natural environment and to become aware of the rights and responsibilities of all.’ Sincerity Sport ‘Self-acceptance sets us free from pretence and defensiveness, Contact Details free to relate honestly and To contact the Sport Department or Ms Gabi Howard ‘The Church recognises sport to be one of the great affectionately..’ (Co-Curricular Leader of Sport), please contact the institutions of our society that helps individuals realise Loreto College Main Reception on (03) 53296100. their human potential and builds up the bonds of the Verity community, fostering communal initiative and ‘Integrity and truth, particularly the profound truth of who we responsibility. are and what gives meaning to our lives.’ 1600 Sturt Street Ballarat As our lifestyles become more and more sedentary, Felicity Victoria Australia 3350 sport makes an essential contribution to our health and ‘Felicity
    [Show full text]
  • Light of Christ
    Catholic Education Keeping the light of Christ TERM 2, 2020 FLEXIBLE AND INTERRELIGIOUS HELP FOR THOSE 2020 CREATIVE AROUND THE 3REMOTE LEARNING 4 CULTURE 6 WHO NEED IT 8 ARTS EXHIBITION 13 ARCHDIOCESE Pandemic Welcome to the second edition of Catholic Education Editorial Today for 2020. Term 2 will be different for us all, as Excerpt taken from a poem by Lynn Ungar we have transitioned to flexible and remote learning (11 March 2020) to support government measures to limit the spread Know that we are connected of coronavirus. These measures will prevent us from in ways that are terrifying and beautiful. coming together physically as school communities (You could hardly deny it now.) during the term. Know that our lives However, as Archbishop Peter has said, the teaching are in one another’s hands. of Jesus shows that even when we are personally (Surely, that has come clear.) or socially isolated, we can remain spiritually and Do not reach out your hands. pastorally together. Reach out your heart. Reach out your words. This term, you are encouraged to work on your Reach out all the tendrils spiritual togetherness as a school community. of compassion that move, invisibly, Find creative ways of reaching out to members of where we cannot touch. your community who might be frightened or worried. Get digital in building bridges of care and concern towards those who are at risk and vulnerable. Pray for the ill and for those family members and medical professionals who are caring for them. Safety remains important, but please do not forget outreach and the responsibility we have to the wellbeing of our community.
    [Show full text]
  • The Alliance of Girls' Schools Australasia
    ANNUAL GENERAL MEETING OF THE ALLIANCE OF GIRLS’ SCHOOLS (AUSTRALASIA) LTD Monday 23 May 2016 BRANCH REPORTS: WESTERN AUSTRALIA All ten girls’ schools in Western Australia are members of AGSA. This year we welcomed two new principal’s to our schools at the beginning of 2015; Kim Keipe at St Hildas Anglican Girls School and Kerrie Fraser at Mercedes College. In Term 4 we also welcomed Dr Kate Hadwen as Principal to Presbyterian Ladies College. In welcoming new principals, we also said farewell to Beth Blackwood who has been Principal at PLC for 18 years. Beth has been a generous contributor to AGSA serving on the National committee during her time at the school. She has been an inspirational leader of a girls’ school in Western Australia. We are fortunate that we will maintain our contact with Beth as the new Executive Officer of AHISA another important educational group. We try and hold at least one AGSA event each term during the year. In Term 1 we held a Year 12 leaders afternoon which was opened up to 6 members of each School’s student leadership team. This event was run by Senior Staff and Student Leaders of Perth College. It provided a rich opportunity for the girls to connect and share their ideas and thoughts on student leadership especially following the Student Leadership Conference that many of our schools sent girls too. In Term 2 we held a networking and dinner at Penrhos College for senior staff. There were approximately 100 people in attendance and we had the opportunity to hear from Cynthia Griffin, US Consul General based in Perth.
    [Show full text]
  • RVOY Honour Roll 1975 Onwards
    ROSTRUM VOICE OF YOUTH NATIONAL FINALISTS Year Nat Final Convenor Zone Coordinator Junior Finalist School Place Senior Finalist School Place National Coordinator 1975 Tom Trebilco ACT Tom Trebilco Fiona Tilley Belconnen HS 1 Linzi Jones 1975 NSW 1975 QLD John Brown Sue Stevens St Monica's College Cairns 3 Michelle Barker 3 1975 SA NA NA NA Sheryn Pitman Methodist Ladies College 2 1975 TAS Mac Blackwood Anthony Ackroyd St Virgils College, Hobart 1 1975 VIC 1975 WA Year Nat Final Convenor Zone Coordinator Junior Finalist School Place Senior Finalist School Place 1976 Tom Trebilco? ACT Tom Trebilco? Tim Hayden Telopea Park HS 1 (tie) 1976 NSW 1976 QLD John Brown Michelle Morgan Brigadine Convent Margaret Paton All Hallows School Brisbane 1976 SA NA NA NA NA NA 1976 TAS Mac Blackwood Lisa Thompson Oakburn College 1 (tie) 1976 VIC 1976 WA Paul Donovan St Louis School 1 Year Nat Final Convenor Zone Coordinator Junior Finalist School Place Senior Finalist School Place 1977 ACT Michelle Regan (sub) Belconnen HS 1977 NSW John White Kerrie Mengerson Coonabarabran HS 1 Sonia Anderson Francis Greenway HS,Maitland 1 1977 QLD Mervyn Green Susan Burrows St Margarets Clayfield Anne Frawley Rockhampton 1977 SA NA NA NA NA NA 1977 TAS Mac Blackwood Julie Smith Burnie High Gabrielle Bennett Launceston 1977 Richard Smillie VIC Pat Taylor Linda Holland St Anne's Warrnambool 3 Kelvin Bicknell Echuca Technical 1977 WA David Johnston Mark Donovan John XX111 College 2 Fiona Gauntlett John XX111 College 2 Year Nat Final Convenor Zone Coordinator Junior Finalist
    [Show full text]
  • Become Part of Our Story YOUR STORY BEGINS Welcome
    Become part of our story YOUR STORY BEGINS Welcome Haere mai ki te Welcome to Columba College, where our aim is tohatoha tō korero to instil in every student a love of learning and an understanding that education matters. For over ki a mātou, kei reira a century, we have been preparing students to contribute and succeed, wherever their path may koe tau ai. take them. Columba is unique. A state-integrated, special character school, it is co-educational from years 0-6, and then Come and share offers single sex girls’ education and boarding from your story with us, years 7-13. Founded as a Presbyterian school in 1915, the and find the place Presbyterian faith has long been associated with where you belong. education, and service within the community. In an inclusive environment, students are taught to respond generously and compassionately, and to look after one another and those within their community. At Columba we have a clear academic focus and encourage excellence in sport and cultural pursuits, while being mindful of each student's wellbeing. Pauline Duthie We teach our students to think creatively and critically Principal in all aspects of their lives and to know that each and everyone of them can make a difference. 2 3 MISSION STATEMENT With grace and good discipline, we are dedicated to all Columba College students being lifelong learners committed to personal excellence, ethical behaviour and service to others. 4 VALUES AND MISSION Our History Columba was founded in 1915, the amalgamation of two earlier girls’ schools, Girton College and Braemar House School.
    [Show full text]
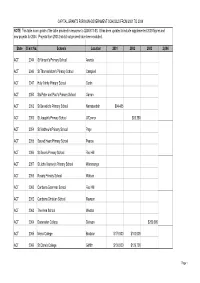
  • Answers to Estimates Questions on Notice
    CAPITAL GRANTS FOR NON-GOVERNMENT SCHOOLS FROM 2001 TO 2004 NOTE: This table is an update of the table provided in response to QON 617-03. It has been updated to include supplemented 2003 figures and new projects for 2004. Projects from 2003 that did not proceed have been excluded. State Client No. Schools Location 2001 2002 2003 2,004 ACT 2044 St Vincent's Primary School Aranda ACT 2046 St Thomas More's Primary School Campbell ACT 2047 Holy Trinity Primary School Curtin ACT 2050 Sts Peter and Paul's Primary School Garran ACT 2052 St Benedict's Primary School Narrabundah $94,485 ACT 2053 St Joseph's Primary School O'Connor $93,280 ACT 2054 St Matthew's Primary School Page ACT 2055 Sacred Heart Primary School Pearce ACT 2056 St Bede's Primary School Red Hill ACT 2057 St John Vianney's Primary School Waramanga ACT 2058 Rosary Primary School Watson ACT 2060 Canberra Grammar School Red Hill ACT 2062 Canberra Christian School Mawson ACT 2063 The Ame School Weston ACT 2064 Daramalan College Dickson $250,000 ACT 2065 Merici College Braddon $176,000 $100,000 ACT 2066 St Clare's College Griffith $130,000 $129,700 Page 1 CAPITAL GRANTS FOR NON-GOVERNMENT SCHOOLS FROM 2001 TO 2004 State Client No. Schools Location 2001 2002 2003 2,004 ACT 2067 Marist College Canberra Pearce ACT 2068 St Edmund's College Griffith ACT 2900 St Thomas Aquinas Primary School Charnwood $105,000 ACT 2902 St Monica's Primary School Evatt ACT 2903 St Francis Xavier College Florey $254,588 $200,000 ACT 2904 St Thomas the Apostle Primary School Kambah ACT 2905 St Anthony's
    [Show full text]
  • Conference Proceedings
    Conference Proceedings Contents Foreword v Keynote papers Professor John Gardner 1 Assessment for teaching: the half-way house. Dr Margaret Forster 5 Informative Assessment – understanding and guiding learning. Professor Helen Wildy 9 Making local meaning from national assessment data: NAPNuLit. Professor Patrik Scheinin 12 Using student assessment to improve teaching and educational policy. Concurrent papers Prue Anderson 15 What makes a difference? How measuring the non-academic outcomes of schooling can help guide school practice. Peter Titmanis 20 Reflections on the validity of using results from large scale assessments at the school level. Professor Helen Timperley 21 Using Assessment Data for improving teaching practice. Juliette Mendelovits and Dara Searle 26 PISA for teachers: Interpreting and using information from an international reading assessment in the classroom. Katrina Spencer and Daniel Balacco 31 Next Practice: What we are learning about teaching from student data. Professor Val Klenowski and Thelma Gertz 36 Culture-fair assessment leading to culturally responsive pedagogy with indigenous students. Jocelyn Cook 44 An Even Start: Innovative resources to suport teachers to better monitor and better support students measured below benchmark. David Wasson 47 Large Cohort Testing - How can we use assessment data to effect school and system improvement? Dr Stephen Humphry and Dr Sandra Heldsinger 57 Do rubics help to inform and direct teaching practices? Poster presentations 63 Conference program 65 Perth Convention and Exhibition
    [Show full text]