DOCSLIB.ORG

Assessing the Effect of Density on Population Growth When Modeling Individual Encounter Data Simone Tenan, Giacomo Tavecchia, Daniel Oro, Roger Pradel

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Assessing the Effect of Density on Population Growth When Modeling Individual Encounter Data Simone Tenan, Giacomo Tavecchia, Daniel Oro, Roger Pradel View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Archive Ouverte en Sciences de l'Information et de la Communication Assessing the effect of density on population growth when modeling individual encounter data Simone Tenan, Giacomo Tavecchia, Daniel Oro, Roger Pradel To cite this version: Simone Tenan, Giacomo Tavecchia, Daniel Oro, Roger Pradel. Assessing the effect of density on population growth when modeling individual encounter data. Ecology, Ecological Society of America, 2019, 100 (3), pp.e02595. 10.1002/ecy.2595. hal-02104959 HAL Id: hal-02104959 https://hal.archives-ouvertes.fr/hal-02104959 Submitted on 19 Apr 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Statistical Reports Ecology, 100(3), 2019, e02595 © 2019 by the Ecological Society of America Assessing the effect of density on population growth when modeling individual encounter data 1,5 2 3 4 SIMONE TENAN, GIACOMO TAVECCHIA, DANIEL ORO, AND ROGER PRADEL 1MUSE - Science Museum, Vertebrate Zoology Section, Corso del Lavoro e della Scienza 3, Trento 38122 Italy 2Animal Ecology and Demography Group, IMEDEA (CSIC-UIB), Miquel Marques 21, Esporles, Mallorca 07190 Spain 3Blanes Centre for Advanced Studies, CEAB (CSIC), C/d’acces a la Cala St. Francesc 14, Blanes 17300 Spain 4CEFE UMR 5175, CNRS, Universite de Montpellier, Universite Paul-Valery Montpellier - EPHE, Montpellier Cedex 5 France Citation: Tenan, S., G. Tavecchia, D. Oro, and R. Pradel. 2019. Assessing the effect of density on population growth when modeling individual encounter data. Ecology 100(3):e02595. 10. 1002/ecy.2595 Abstract. The relative role of density-dependent and density-independent variation in vital rates and population size remains largely unsolved. Despite its importance to the theory and application of population ecology, and to conservation biology, quantifying the role and strength of density dependence is particularly challenging. We present a hierarchical formula- tion of the temporal symmetry approach, also known as the Pradel model, that permits estima- tion of the strength of density dependence from capture–mark–reencounter data. A measure of relative population size is built in the model and serves to detect density dependence directly on population growth rate. The model is also extended to account for temporal random vari- ability in demographic rates, allowing estimation of the temporal variance of population growth rate unexplained by density dependence. We thus present a model-based approach that enable to test and quantify the effect of density-dependent and density-independent factors affecting population fluctuations in a single modeling framework. More generally, we use this modeling framework along with simulated and empirical data to show the value of including density dependence when modeling individual encounter data without the need for auxiliary data. Key words: Audouin’s Gull; capture-recapture; Gibbs variable selection; open population estimation; population dynamics; Pradel model; rate of population change; temporal symmetry model. of density dependence is thus fundamental to the under- INTRODUCTION standing of processes that regulate temporal and spatial Because a population cannot grow indefinitely, it is variation in population size (Lack 1954, Ricker 1954, expected that density will eventually check population Andrewartha and Birch 1986). growth (Malthus 1798). At the opposite, low levels of It has always been challenging to demonstrate density density have also been found to sometimes limit popula- dependence in real populations. There are practical, the- tion growth (Allee et al. 1949). The first phenomenon oretical, and technical difficulties in tackling the prob- (negative density dependence) will result in population lem (Lebreton 2009). First, population size and hence fluctuations around the carrying capacity (Sibly and density is notoriously difficult to measure accurately; Hone 2002) while the second (positive density depen- second, density is only a proxy for interactions among dence) will precipitate population decline. It follows that individuals and is thus a noisy measure of what actually the way density regulates population dynamics influ- occurs; but probably the main obstacle is statistical: suc- ences persistence time of threatened populations as well cessive densities and changes in density are obviously as the sustainable harvest rate of exploited populations strongly related, a fact that must be acknowledged in (Lande et al. 2003). The study of the strength and form any model. Early attempts focused on fitting the theoret- ical logistic growth model (Verhulst 1838, Pearl and Manuscript received 25 May 2018; revised 6 November 2018; Reed 1920) but were inconclusive (Slobodkin 2001). accepted 3 December 2018. Corresponding Editor: Brett T. Among the extant approaches, retrospective studies ana- McClintock. 5 E-mail: [email protected] lyze variation of population growth rate over time by Article e02595; page 1 Article e02595; page 2 SIMONE TENAN ET AL. Ecology, Vol. 100, No. 3 focusing on the realized population growth rate between where the latter includes both local recruitment and two successive time steps as qi = Ni+1/Ni, where Ni is immigration, and estimated mortality includes perma- population size at time i. However, abundance estima- nent emigration. However, the Pradel model likelihood tion in open populations can be biased when the error in can be parameterized with population growth rate q as a the counts around the true population size (observation structural parameter, thus allowing to test biological error) is not accounted for, leading to spurious detection hypotheses directly on q. In addition, a Bayesian formu- of density dependence (Dennis et al. 2006, Freckleton lation of the Pradel model permits the hierarchical mod- et al. 2006, Lebreton 2009). State-space models is elling of the biological and sampling processes and another approach that can reduce bias in parameter esti- allows the extension of the original fixed time effects mates when population counts are the only data avail- structure to random time effects (Tenan et al. 2014b). able (Clark and Bjørnstad 2004), however separating At this point, density can be integrated in the model, observation variance from process variance is only possi- only as an external covariate. This is not very satisfac- ble when the observation error is relatively small (Knape tory as the changes in density and population growth 2008). In addition, negative autocorrelation between are obviously related and considering an external mea- successive estimators may lead to an overestimation of sure of density and the population growth rate parame- temporal variance of population growth rate (an overes- ters of the model as independent is obviously wrong. In timation of Ni biases qi low but biases qiÀ1 high). this paper we derive a measure of relative population Some methods, based on individual encounter histo- size directly from the CMR data, and use it to detect ries, are currently available to assess the impact of density density dependence within the same model. In this way, on demographic rates while accounting for imperfect we circumvent the statistical difficulty inherent in den- detection. Schofield and Barker (2008) and Schofield sity-dependent models of having the same quantity, et al. (2009) propose to study the effect of density on namely density, at the same time estimated and the dri- recruitment and survival. However, density dependence ver of its own changes. may be effected differently in different years. For instance, Here we propose a new Bayesian hierarchical formula- eports for a given density, it may entail a reduced survival in tion of the temporal symmetry approach that allows years of high fecundity whereas survival will remain high quantification of the effect of population size on in years of low fecundity. Methods that allow to study the population growth rate and, more generally, the study R effect of density directly on population growth rate are of density-dependent and density-independent (i.e., thus needed. The approach proposed by Schofield et al. environmental) factors that affect temporal variation of (2009) can be reparameterized so that recruitment rate is population growth rate. Such decomposition into deter- defined as the difference between population growth rate ministic and stochastic components is important to the and survival (Nichols 2016) thus allowing modeling in assessment of the effects of environmental change on terms of population growth rate. population dynamics. Integrated population models (IPMs; Besbeas et al. We illustrate the modeling approach with simulated 2002) allow estimation of the strength of density depen- data, to investigate the effectiveness of detecting density- dence not only on demographic rates but also on the dependent effects on population growth rate, and we derived population growth rate (Abadi et al. 2012). apply the approach to encounter histories of a long-lived However,
Load more

Recommended publications
  • Modeling Techniques
    Appendix A Modeling Techniques A.1 Population Growth Models Using Differential Equations Our main goal here is to introduce a few modeling techniques we use throughout this book. We do not intend however to provide here the fundamentals on modeling, a tutorial or a review. For these, we refer to other sources (DeAngelis et al. 1992; Ford 2009; Grimm et al. 2006; Kuang 1993). This Appendix is rather a refresher as well as an example of why using different modeling techniques for one and the same problem can be beneficial to understand biological processes better. We start with the simple exponential population growth to make modeling accessible even to complete beginners. Biologists generally define a population as a collection of individuals that belong to the same species and can potentially breed with each other. One of the best-known early models on population growth was outlined by Malthus (1798). He famously maintained that the human population is predicted to grow in an exponential manner, but the crucial products needed to sustain the population grow in but a linear manner. He argued that these different types of growths will trigger disasters when the population’s needs are not satisfied. The basic exponential growth model consists of a single positive feedback loop that arises from the fact that every individual (N) is predicted to have a fixed number of offspring (r), regardless of the size of the population, and thus also regardless of the remaining resources in the habitat: dN = rN dt (A.1.1) This exponential growth model had a profound effect on biology such as developing the theory of natural selection (Darwin 1859).
    [Show full text]
  • Density Dependence in Demography and Dispersal Generates Fluctuating
    Density dependence in demography and dispersal generates fluctuating invasion speeds Lauren L. Sullivana,1, Bingtuan Lib, Tom E. X. Millerc, Michael G. Neubertd, and Allison K. Shawa aDepartment of Ecology, Evolution and Behavior, University of Minnesota, Saint Paul, MN 55108; bDepartment of Mathematics, University of Louisville, Louisville, KY 40292; cDepartment of BioSciences, Program in Ecology and Evolutionary Biology, Rice University, Houston, TX 77005; and dBiology Department, Woods Hole Oceanographic Institution, Woods Hole, MA 02543 Edited by Alan Hastings, University of California, Davis, CA, and approved March 30, 2017 (received for review November 23, 2016) Density dependence plays an important role in population regu- is driven by reproduction and dispersal from high-density pop- lation and is known to generate temporal fluctuations in popu- ulations behind the invasion front (13–15)]. The conventional lation density. However, the ways in which density dependence wisdom of a long-term constant invasion speed is widely applied affects spatial population processes, such as species invasions, (16, 17). are less understood. Although classical ecological theory suggests In contrast to classic approaches that emphasize a long-term that invasions should advance at a constant speed, empirical work constant speed, there is growing empirical recognition that inva- is illuminating the highly variable nature of biological invasions, sion dynamics can be highly variable and idiosyncratic (18–25). which often exhibit nonconstant spreading speeds, even in sim- There are several theoretical explanations for fluctuations in ple, controlled settings. Here, we explore endogenous density invasion speed (which we define here as any persistent tem- dependence as a mechanism for inducing variability in biologi- poral variability in spreading speed), including stochasticity in cal invasions with a set of population models that incorporate either demography or dispersal (24–28) and temporal or spatial density dependence in demographic and dispersal parameters.
    [Show full text]
  • Plant Diversity Increases with the Strength of Negative Density Dependence at the Global Scale
    RESEARCH FOREST ECOLOGY predators, pathogens, or herbivores) and/or com- petition for space and resources (2–4, 7). Numer- ous studies have documented the existence of CNDD in one or several plant species (8–12), and Plant diversity increases with the most of these studies explicitly or implicitly as- sume that stronger CNDD maintains higher spe- strength of negative density cies diversity in communities. However, only a handful of studies have explicitly examined dependence at the global scale the link between CNDD and species diversity (4, 11, 13, 14),andnostudyhasexaminedthis relationship across temperate and tropical lat- Joseph A. LaManna,1,2* Scott A. Mangan,2 Alfonso Alonso,3 Norman A. Bourg,4,5 itudes. Despite decades of study, our understand- Warren Y. Brockelman,6,7 Sarayudh Bunyavejchewin,8 Li-Wan Chang,9 ing of how processes at local scales—such as Jyh-Min Chiang,10 George B. Chuyong,11 Keith Clay,12 Richard Condit,13 density-dependent biotic interactions—influence Susan Cordell,14 Stuart J. Davies,15,16 Tucker J. Furniss,17 Christian P. Giardina,14 18 18 19,20 global patterns of biodiversity remains in flux I. A. U. Nimal Gunatilleke, C. V. Savitri Gunatilleke, Fangliang He, 1 15 21 22 23 ( , ). Robert W. Howe, Stephen P. Hubbell, Chang-Fu Hsieh, Both species-specific and more generalized 14 24 25 15,16 Faith M. Inman-Narahari, David Janík, Daniel J. Johnson, David Kenfack, mechanisms can cause CNDD, but only CNDD 3 24 26 17 Lisa Korte, Kamil Král, Andrew J. Larson, James A. Lutz, caused by species-specific mechanisms can main- 27,28 4 29 Sean M.
    [Show full text]
  • "Density Dependence and Independence"
    Density Dependence and Advanced article Independence Article Contents . Introduction: Concepts and Importance in Ecology Mark A Hixon, Oregon State University, Corvallis, Oregon, USA . Mechanisms of Density Dependence . Old Debates Resolved Darren W Johnson, Oregon State University, Corvallis, Oregon, USA . Detecting Density Dependence . Future Directions Online posting date: 15th December 2009 Density dependence occurs when the population growth parameter of interest involves population dynamics, rate, or constituent gain rates (e.g. birth and immi- including the population growth rate and the four primary gration) or loss rates (death and emigration), vary caus- demographic (or vital) rates – birth, death, immigration ally with population size or density (N). When these and emigration – although related parameters, such as growth and fecundity, are also investigated. See also: parameters do not vary with N, they are density-inde- Population Dynamics: Introduction pendent. Direct density dependence, where the popu- Use of the words ‘density dependence’ alone normally lation growth rate or gain rates vary as a negative means ‘direct density dependence’ (or compensation): the function of N, or the loss rates vary as a positive function of per capita (proportional) gain rate (population or indi- N, is necessary but not always sufficient for population vidual growth, fecundity, birth or immigration) decreases regulation. The opposite patterns, inverse density as N increases (Figure 1a) or the loss rate (death and/or dependence or the Allee effect, may push endangered emigration) increases as N increases (Figure 1b). The populations towards extinction. Direct density depend- opposite patterns are called inverse density dependence (or ence is caused by competition, and at times, predation.
    [Show full text]
  • Literature Cited in Lizards Natural History Database
    Literature Cited in Lizards Natural History database Abdala, C. S., A. S. Quinteros, and R. E. Espinoza. 2008. Two new species of Liolaemus (Iguania: Liolaemidae) from the puna of northwestern Argentina. Herpetologica 64:458-471. Abdala, C. S., D. Baldo, R. A. Juárez, and R. E. Espinoza. 2016. The first parthenogenetic pleurodont Iguanian: a new all-female Liolaemus (Squamata: Liolaemidae) from western Argentina. Copeia 104:487-497. Abdala, C. S., J. C. Acosta, M. R. Cabrera, H. J. Villaviciencio, and J. Marinero. 2009. A new Andean Liolaemus of the L. montanus series (Squamata: Iguania: Liolaemidae) from western Argentina. South American Journal of Herpetology 4:91-102. Abdala, C. S., J. L. Acosta, J. C. Acosta, B. B. Alvarez, F. Arias, L. J. Avila, . S. M. Zalba. 2012. Categorización del estado de conservación de las lagartijas y anfisbenas de la República Argentina. Cuadernos de Herpetologia 26 (Suppl. 1):215-248. Abell, A. J. 1999. Male-female spacing patterns in the lizard, Sceloporus virgatus. Amphibia-Reptilia 20:185-194. Abts, M. L. 1987. Environment and variation in life history traits of the Chuckwalla, Sauromalus obesus. Ecological Monographs 57:215-232. Achaval, F., and A. Olmos. 2003. Anfibios y reptiles del Uruguay. Montevideo, Uruguay: Facultad de Ciencias. Achaval, F., and A. Olmos. 2007. Anfibio y reptiles del Uruguay, 3rd edn. Montevideo, Uruguay: Serie Fauna 1. Ackermann, T. 2006. Schreibers Glatkopfleguan Leiocephalus schreibersii. Munich, Germany: Natur und Tier. Ackley, J. W., P. J. Muelleman, R. E. Carter, R. W. Henderson, and R. Powell. 2009. A rapid assessment of herpetofaunal diversity in variously altered habitats on Dominica.
    [Show full text]
  • STAGE STRUCTURE, DENSITY DEPENDENCE and the EFFICACY of MARINE RESERVES Colette M. St. Mary, Craig W. Osenberg, Thomas K. Frazer
    BULLETIN OF MARINE SCIENCE, 66(3): 675–690, 2000 STAGE STRUCTURE, DENSITY DEPENDENCE AND THE EFFICACY OF MARINE RESERVES Colette M. St. Mary, Craig W. Osenberg, Thomas K. Frazer and William J. Lindberg ABSTRACT The habitat requirements of fishes and other marine organisms often change with on- togeny, so many harvested species exhibit such extreme large-scale spatial segregation between life stages that all life stages cannot be protected within a single marine reserve. Nevertheless, most discussions of marine reserves have focused narrowly on single life- history events (e.g., reproduction or settlement) or a single life stage (e.g., adult or re- cruit). Instead, we hypothesize that an effective marine reserve system should often in- clude a diversity of protected habitats, each appropriate to a different life stage. In such a case, the spatial configuration of habitats within reserves, and of separate reserves across larger spatial scales, may affect how marine resources respond to reserve design. We explored these issues by developing a mathematical model of a fish population consist- ing of two benthic life stages (juvenile and adult) that use spatially distinct habitats and examined the population’s response to various management scenarios. Specifically, we varied the sizes of reserves protecting the two life stages and the degree of coupling between juvenile and adult reserves (i.e., the fraction of the protected juvenile stock that migrates into the adult reserve upon maturation). We examined the effects when density dependence operated in only the juvenile stage, only the adult stage, or both. The results demonstrated that population stage structure and the nature of density dependence should be incorporated into the design of marine reserves but did not provide robust support for the general tenet that all life stages must be protected for an effective reserve system.
    [Show full text]
  • DENSITY DEPENDENCE, the LOGISTIC EQUATION, and R- AUD
    89 DENSITY DEPENDENCE,THE LOGISTIC EQUATION, AND r- AUD K-SELECTION: A CRITIQUE AI{D AN AJ,TERNATIVEAPPROACH Jan Kozlowski Department of Animal Ecology Jagiellonlan University Karasia 6 30-060 Krak6w, POLAND Received September 18,1978; July 9, 1980 ABSTRACT: The logistic equation is a starting point of many ecological theories. Most ecologists agree that this equation is usually not conslstent Iillth observations and experlmental results but it ls argued that the slmpllclty of fhis equatlon ls the reason for this lnconsistency. In this paper I attempt to prove that the reason for inadequacy of the logistic equation l-s more fundamental: most systems qf equa- tions descrlbing the dynamlcs of population and lts resources cannot be transformed to the single equatlon for limited growth. Even if thls transformation is posslble' the K parameter depends on components of !r usually on the ratLo of mortallty rate to reproduction rate. Thls fact ls commonly overlooked because it ls assuned that denslty affects the abstract term r (popul-atlon growth rate). Because of doubts as to density-dependence and the logistlc equation, the r- and K-selectlon concept is criticLzed, both as a classiflcation system and as a predlctlve theory. It ls shown that when resources are explicltly consldered, it ls possible to prediet traits favored by natural- selectLon on a given resource level dlrectly from the descrlptlon of the system. This approach seems to be more advan- tageous than the r- and K-selection concept. I. INTRODUCTION Ttre logistic equation is a mathematical formulation of the denslty-dependent facEors concept. Though density-dependence may no longer be a burning issue lt ls dlfflcult to flnd a contemporary ecology textbook that does not contaln the loglstlc equation.
    [Show full text]
  • Drechslerella Stenobrocha Genome Illustrates the Mechanism Of
    Liu et al. BMC Genomics 2014, 15:114 http://www.biomedcentral.com/1471-2164/15/114 RESEARCH ARTICLE Open Access Drechslerella stenobrocha genome illustrates the mechanism of constricting rings and the origin of nematode predation in fungi Keke Liu1,2†, Weiwei Zhang1,2†, Yiling Lai1,2, Meichun Xiang1, Xiuna Wang1, Xinyu Zhang1 and Xingzhong Liu1* Abstract Background: Nematode-trapping fungi are a unique group of organisms that can capture nematodes using sophisticated trapping structures. The genome of Drechslerella stenobrocha, a constricting-ring-forming fungus, has been sequenced and reported, and provided new insights into the evolutionary origins of nematode predation in fungi, the trapping mechanisms, and the dual lifestyles of saprophagy and predation. Results: The genome of the fungus Drechslerella stenobrocha, which mechanically traps nematodes using a constricting ring, was sequenced. The genome was 29.02 Mb in size and was found rare instances of transposons and repeat induced point mutations, than that of Arthrobotrys oligospora. The functional proteins involved in nematode-infection, such as chitinases, subtilisins, and adhesive proteins, underwent a significant expansion in the A. oligospora genome, while there were fewer lectin genes that mediate fungus-nematode recognition in the D. stenobrocha genome. The carbohydrate-degrading enzyme catalogs in both species were similar to those of efficient cellulolytic fungi, suggesting a saprophytic origin of nematode-trapping fungi. In D. stenobrocha, the down-regulation of saprophytic enzyme genes and the up-regulation of infection-related genes during the capture of nematodes indicated a transition between dual life strategies of saprophagy and predation. The transcriptional profiles also indicated that trap formation was related to the protein kinase C (PKC) signal pathway and regulated by Zn(2)–C6 type transcription factors.
    [Show full text]
  • Counterintuitive Density-Dependent Growth in a Long-Lived Vertebrate After Removal of Nest Predators Ricky-John Spencer Iowa State University
    CORE Metadata, citation and similar papers at core.ac.uk Provided by Digital Repository @ Iowa State University Ecology, Evolution and Organismal Biology Ecology, Evolution and Organismal Biology Publications 12-2006 Counterintuitive density-dependent growth in a long-lived vertebrate after removal of nest predators Ricky-John Spencer Iowa State University Fredric J. Janzen Iowa State University, [email protected] Michael B. Thompson University of Sydney Follow this and additional works at: http://lib.dr.iastate.edu/eeob_ag_pubs Part of the Evolution Commons, and the Population Biology Commons The ompc lete bibliographic information for this item can be found at http://lib.dr.iastate.edu/ eeob_ag_pubs/151. For information on how to cite this item, please visit http://lib.dr.iastate.edu/ howtocite.html. This Article is brought to you for free and open access by the Ecology, Evolution and Organismal Biology at Iowa State University Digital Repository. It has been accepted for inclusion in Ecology, Evolution and Organismal Biology Publications by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Counterintuitive density-dependent growth in a long-lived vertebrate after removal of nest predators Abstract Examining the phenotypic and genetic underpinnings of life-history variation in long-lived organisms is central to the study of life-history evolution. Juvenile growth and survival are often density dependent in reptiles, and theory predicts the evolution of slow growth in response to low resources (resource-limiting hypothesis), such as under densely populated conditions. However, rapid growth is predicted when exceeding some critical body size reduces the risk of mortality (mortality hypothesis).
    [Show full text]
  • 2 Wildebeest in the Serengeti: Limits to Exponential Growth
    Case Studies in Ecology and Evolution DRAFT 2 Wildebeest in the Serengeti: limits to exponential growth In the previous chapter we saw the power of exponential population growth. Even small rates of increase will eventually lead to very large populations if r stays constant. At the beginning of the 19th century Thomas Malthus wrote extensively about the power of exponential growth, pointing out that no population can continue to grow forever. Eventually the numbers of individuals will get so large that they must run out of resources. While Malthus was particularly interested in human populations, the same must be true for all kinds of species. No population can grow exponentially forever. Charles Darwin used those ideas as one of the cornerstones of his theory of natural selection. Because of the speed at which exponentially growing populations can increase in size, very few populations in nature will show exponential growth. Once a population has reached sufficient size to balance the available resource supply, there should be only minor fluctuations in numbers. Only when there is a large perturbation of the environment, such as the introduction of a species to a new area or severe reduction in population size due to hunting or disease will you find populations increasing in an exponential manner. One very well studied system for looking at population dynamics is the wildebeest Figure 2.1. top: Herd of Wildebeest. Bottom: Map (Connochaetes taurinus) on the Serengeti plains of the Serengeti-Mara ecosystem showing the of East Africa. Anthony Sinclair and Simon annual migration route. Mduma from the University of British Columbia have been studying them for 3 decades and have generated a long time series of records of population abundance.
    [Show full text]
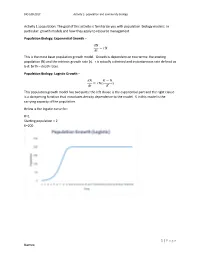
  • 1 | Page Names: Activity 1: Population: the Goal of This Activity
    BIO 108-2017 Activity 2- population and community biology Activity 1: population: The goal of this activity is familiarize you with population biology models: In particular: growth models and how they apply to resource management Population Biology: Exponential Growth – 푑푁 = 푟푁 푑푡 This is the most basic population growth model. Growth is dependent on two terms: the existing population (N) and the intrinsic growth rate (r). r is actually a derived and instantaneous rate defined as b-d: birth – death rates. Population Biology: Logistic Growth – 푑푁 퐾 − 푁 = 푟푁( ) 푑푡 퐾 This population growth model has two parts: the left clause is the exponential part and the right clause is a dampening function that introduces density dependence to the model. K in this model is the carrying capacity of the population. Below is the logistic curve for: R=1 Starting population = 2 K=200 1 | P a g e Names: BIO 108-2017 Activity 2- population and community biology The logistic equation shown above is written in its derivative form. Recall from calculus that the second derivative of an equation can be used to determine the minimum and maximum rate of change in a population. The maximum rate of change is the point on the graph above where the population grows fastest. It is the maximum instantaneous slope. Why would we want to know this? Because it has been used as a target for management of harvested species, especially in fisheries. The idea is that harvest of populations to a size equal to the population where growth rate is highest maximizes sustainable harvest.
    [Show full text]
  • Arxiv:2009.11357V3 [Physics.Bio-Ph] 18 Apr 2021 H Rbblt Itiuino H Otrcn Common Recent Most 15]
    Virus-host interactions shape viral dispersal giving rise to distinct classes of travelling waves in spatial expansions 1 1 1, 2 3, 4 1, Michael Hunter, Nikhil Krishnan, Tongfei Liu, Wolfram M¨obius, and Diana Fusco ∗ 1Cavendish Laboratory, University of Cambridge, Cambridge, CB3 0HE, United Kingdom 2Department of Physics, University of Oxford, Oxford, OX1 3PJ, United Kingdom 3Living Systems Institute, University of Exeter, Exeter, EX4 4QD, UK 4Physics and Astronomy, College of Engineering, Mathematics and Physical Sciences, University of Exeter, Exeter, EX4 4QL, UK (Dated: April 20, 2021) Reaction-diffusion waves have long been used to describe the growth and spread of populations undergoing a spatial range expansion. Such waves are generally classed as either pulled, where the dynamics are driven by the very tip of the front and stochastic fluctuations are high, or pushed, where cooperation in growth or dispersal results in a bulk-driven wave in which fluctuations are suppressed. These concepts have been well studied experimentally in populations where the cooperation leads to a density-dependent growth rate. By contrast, relatively little is known about experimental populations that exhibit density-dependent dispersal. Using bacteriophage T7 as a test organism, we present novel experimental measurements that demonstrate that the diffusion of phage T7, in a lawn of host E. coli, is hindered by steric interactions with host bacteria cells. The coupling between host density, phage dispersal and cell lysis caused by viral infection results in an effective density-dependent diffusion coefficient akin to cooperative behavior. Using a system of reaction-diffusion equations, we show that this effect can result in a transition from a pulled to pushed expansion.
    [Show full text]