Physics 6775 – G. Laicher Spring 2012 Lab 7 Part 1: Background Lecture ‐ Spectrometer
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

3 Specular Reflection Spectroscopy
3 Specular Reflection Spectroscopy Robert J. Lipert, Brian D. Lamp, and Marc D. Porter 3.1 INTRODUCTION This chapter on specular reflection spectroscopy focuses on applications in the mid-infrared region of the spectrum. Applications in other spectral regions or using other spectroscopic techniques, such as Raman spectros copy, generally follow similar patterns as discussed in this chapter. In the past few decades, infrared spectroscopy (IRS) has developed into an invaluable diagnostic tool for unraveling details about the bonding and molecular structure at surfaces [l, 2, 3, 4, 5, 6]. The importance of IRS derives from five major factors, The first and most critical factor is the role of interfacial phenomena in a vast number of emerging material and surface technologies. Examples include adhesion, catalysis, tribiology, microelec tronics, and electrochemistry [3, 7, 8, 9]. The second factor stems from the Modern Techniques in Applied Molecular Spectroscopy, Edited by Francis M. Mirabella. Techniques in Analytical Chemistry Series. ISBN 0-471-12359-5 © 1998 John Wiley & Sons, Inc. 83 84 Specular Reflection Spectroscopy information-rich content of an IRS spectrum of a surface. That is, the frequencies of the spectroscopic features can be used to identify the chemical composition of a surface and the magnitudes and polarization dependencies of the features used to determine average structural orientations. The third factor arises from advances in the performance of IRS instrumentation. The most important of these advancements are the high throughput and multi plex advantages of Fourier transform interferometry, the development of high sensitivity, low-noise IR detectors, and the improvement in the com putational rates of personal computers and their adaptation to the oper ation of chemical instrumentation. -

Reflection Measurements in IR Spectroscopy Author: Richard Spragg Perkinelmer, Inc
TECHNICAL NOTE Reflection Measurements in IR Spectroscopy Author: Richard Spragg PerkinElmer, Inc. Seer Green, UK Reflection spectra Most materials absorb infrared radiation very strongly. As a result samples have to be prepared as thin films or diluted in non- absorbing matrices in order to measure their spectra in transmission. There is no such limitation on measuring spectra by reflection, so that this is a more versatile way to obtain spectroscopic information. However reflection spectra often look quite different from transmission spectra of the same material. Here we look at the nature of reflection spectra and see when they are likely to provide useful information. This discussion considers only methods for obtaining so-called external reflection spectra not ATR techniques. The nature of reflection spectra The absorption spectrum can be calculated from the measured reflection spectrum by a mathematical operation called the Kramers-Kronig transformation. This is provided in most data manipulation packages used with FTIR spectrometers. Below is a comparison between the absorption spectrum of polymethylmethacrylate obtained by Kramers-Kronig transformation of the reflection spectrum and the transmission spectrum of a thin film. Figure 1. Reflection and transmission at a plane surface Reflection takes place at surfaces. When radiation strikes a surface it may be reflected, transmitted or absorbed. The relative amounts of reflection and transmission are determined by the refractive indices of the two media and the angle of incidence. In the common case of radiation in air striking the surface of a non-absorbing medium with refractive index n at normal incidence the reflection is given by (n-1)2/(n+1)2. -

FTIR Reflection Techniques
FT-IR Reflection Techniques Vladimír Setnička Overview – Main Principles of Reflection Techniques Internal Reflection External Reflection Summary Differences Between Transmission and Reflection FT-IR Techniques Transmission: • Excellent for solids, liquids and gases • The reference method for quantitative analysis • Sample preparation can be difficult Reflection: • Collect light reflected from an interface air/sample, solid/sample, liquid/sample • Analyze liquids, solids, gels or coatings • Minimal sample preparation • Convenient for qualitative analysis, frequently used for quantitative analysis FT-IR Reflection Techniques Internal Reflection Spectroscopy: Attenuated Total Reflection (ATR) External Reflection Spectroscopy: Specular Reflection (smooth surfaces) Combination of Internal and External Reflection: Diffuse Reflection (DRIFTs) (rough surfaces) FT-IR Reflection Techniques • Infrared beam reflects from a interface via total internal reflectance • Sample must be in optical contact with the crystal • Collected information is from the surface • Solids and powders, diluted in a IR transparent matrix if needed • Information provided is from the bulk matrix • Sample must be reflective or on a reflective surface • Information provided is from the thin layers Attenuated Total Reflection (ATR) - introduced in the 1960s, now widely used - light introduced into a suitable prism at an angle exceeding the critical angle for internal reflection an evanescent wave at the reflecting surface • sample in close contact Single Bounce ATR with IRE -

Reflectance IR Spectroscopy, Khoshhesab
11 Reflectance IR Spectroscopy Zahra Monsef Khoshhesab Payame Noor University Department of Chemistry Iran 1. Introduction Infrared spectroscopy is study of the interaction of radiation with molecular vibrations which can be used for a wide range of sample types either in bulk or in microscopic amounts over a wide range of temperatures and physical states. As was discussed in the previous chapters, an infrared spectrum is commonly obtained by passing infrared radiation through a sample and determining what fraction of the incident radiation is absorbed at a particular energy (the energy at which any peak in an absorption spectrum appears corresponds to the frequency of a vibration of a part of a sample molecule). Aside from the conventional IR spectroscopy of measuring light transmitted from the sample, the reflection IR spectroscopy was developed using combination of IR spectroscopy with reflection theories. In the reflection spectroscopy techniques, the absorption properties of a sample can be extracted from the reflected light. Reflectance techniques may be used for samples that are difficult to analyze by the conventional transmittance method. In all, reflectance techniques can be divided into two categories: internal reflection and external reflection. In internal reflection method, interaction of the electromagnetic radiation on the interface between the sample and a medium with a higher refraction index is studied, while external reflectance techniques arise from the radiation reflected from the sample surface. External reflection covers two different types of reflection: specular (regular) reflection and diffuse reflection. The former usually associated with reflection from smooth, polished surfaces like mirror, and the latter associated with the reflection from rough surfaces. -
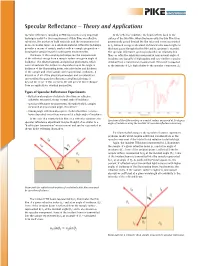
Specular Reflectance – Theory and Applications
Specular Reflectance – Theory and Applications Specular reflectance sampling in FTIR represents a very important At the reflective substrate, the beam reflects back to the technique useful for the measurement of thin films on reflective surface of the thin film. When the beam exits the thin film it has substrates, the analysis of bulk materials and the measurement of geometrically passed through the film twice and is now represented mono-molecular layers on a substrate material. Often this technique as IA. Infrared energy is absorbed at characteristic wavelengths as provides a means of sample analysis with no sample preparation – this beam passes through the thin film and its spectrum is recorded. keeping the sample intact for subsequent measurements. The specular reflectance spectra produced from relatively thin The basics of the sampling technique involve measurement films on reflective substrates measured at near-normal angle of of the reflected energy from a sample surface at a given angle of incidence are typically of high quality and very similar to spectra incidence. The electromagnetic and physical phenomena which obtained from a transmission measurement. This result is expected occur at and near the surface are dependent upon the angle of as the intensity of IA is high relative to the specular component (IR ). incidence of the illuminating beam, refractive index and thickness of the sample and other sample and experimental conditions. A discussion of all of the physical parameters and considerations surrounding the specular reflectance -

Specular Reflection on Titan: Liquids in Kraken Mare Katrin Stephan,1 Ralf Jaumann,1,2 Robert H
GEOPHYSICAL RESEARCH LETTERS, VOL. 37, L07104, doi:10.1029/2009GL042312, 2010 Click Here for Full Article Specular reflection on Titan: Liquids in Kraken Mare Katrin Stephan,1 Ralf Jaumann,1,2 Robert H. Brown,3 Jason M. Soderblom,3 Laurence A. Soderblom,4 Jason W. Barnes,5 Christophe Sotin,6 Caitlin A. Griffith,3 Randolph L. Kirk,4 Kevin H. Baines,6 Bonnie J. Buratti,6 Roger N. Clark,7 Dyer M. Lytle,3 Robert M. Nelson,6 and Phillip D. Nicholson8 Received 4 January 2010; revised 22 February 2010; accepted 25 February 2010; published 7 April 2010. [1] After more than 50 close flybys of Titan by the Cassini reflections results either because the putative lakes are not spacecraft, it has become evident that features similar in filled with liquids or the lakes have not been observed in morphology to terrestrial lakes and seas exist in Titan’s specular geometry. A further impediment is that the northern polar regions. As Titan progresses into northern spring, polar region, where several extensive features exists, including the much more numerous and larger lakes and seas in the the more than 1000 km wide Kraken Mare [Stofan et al., north‐polar region suggested by Cassini RADAR data, are 2007; Turtle et al., 2009], was not illuminated during Titan’s becoming directly illuminated for the first time since the long winter. Nevertheless, the northern polar region is now arrival of the Cassini spacecraft. This allows the Cassini illuminated for the first time since Cassini arrived at Saturn in optical instruments to search for specular reflections to 2004, thus searches for specular reflections from northern provide further confirmation that liquids are present in bodies of liquid on Titan are now possible, with our first these evident lakes. -

Method of Determining the Optical Properties of Ceramics and Ceramic Pigments: Measurement of the Refractive Index
CASTELLÓN (SPAIN) METHOD OF DETERMINING THE OPTICAL PROPERTIES OF CERAMICS AND CERAMIC PIGMENTS: MEASUREMENT OF THE REFRACTIVE INDEX A. Tolosa(1), N. Alcón(1), F. Sanmiguel(2), O. Ruiz(2). (1) AIDO, Instituto tecnológico de Óptica, Color e Imagen, Spain. (2) Torrecid, S.A., Spain. ABSTRACT The knowledge of the optical properties of materials, such as pigments or the ceramics that contain these, is a key feature in modelling the behaviour of light when it impinges upon them. This paper presents a method of obtaining the refractive index of ceramics from diffuse reflectance measurements made with a spectrophotometer equipped with an integrating sphere. The method has been demonstrated to be applicable to opaque ceramics, independently of whether the surface is polished or not, thus avoiding the need to use different methods to measure the refractive index accor- ding to the surface characteristics of the material. This method allows the Fresnel equations to be directly used to calculate the refractive index with the measured diffuse reflectance, without needing to measure just the specular reflectance. Al- ternatively, the method could also be used to measure the refractive index in transparent and translucent samples. The technique can be adapted to determine the complex refractive index of pigments. The reflectance measurement would be based on the method proposed in this paper, but for the calculation of the real part of the refractive index, related to the change in velocity that light undergoes when it reaches the material, and the imaginary part, related to light absorption by the material, the Kramers-Kronig relations would be used. -

On the Role of the Process of Reflection in Radio Wave Propagationl F
JOURNAL OF RESEARCH of the National Bureau of Standards- D. Radio Propagation Vol. 66D, No.3, May- June 1962 On the Role of the Process of Reflection In Radio Wave Propagationl F. du Castel, P. Misme, A. Spizzichino, and 1. Voge Contribution from Centre National d'Etudes des Telecommunications, France (Received August 21 , 196J ; revi sed December 9, ] 96 1) Nature offers numerous examples of irregular stratification of t he medium for t he p ro p:t gatio n of radio waves. A st udy of t he process of refl ection in such a mcdium di sting ui shes between specular reflection and d iffu se refl ection. The phenomenon of trans-ho ri zo n tropospheric propagation offers an ex ample of t he appli cation of such a process, necessar." for t he interpretation of experimental results. Other examples a re t hose of ionospheric propagation (sporadic-E laycr) a nd propagation over a n irregula r ground surfact' (phenom enon of a lbedo). 1. Introduction This paper discusses the role of partial r efi ec tion in the propagation o/" radio waves in stratified media. This work drffers considerably from other works by different authors a bout the same problem [Epstein , 1930; F einstein, 1951 and 1952; Wait, 1952; Carroll et aI. , 1955 ; Friis et aI., 1957 ; Smyth et aI. , 1957] . The authors wer e led to make such a study in th e co urse of seeking an interpretation of experimen tal 5 results obtained in trans-horizon tropospheric propa gation for which the classical theory of turbulent scattering did not appear to give a satisfactory ex planation. -

Advanced Ray Tracing
Advanced Ray Tracing (Recursive)(Recursive) RayRay TracingTracing AntialiasingAntialiasing MotionMotion BlurBlur DistributionDistribution RayRay TracingTracing RayRay TracingTracing andand RadiosityRadiosity Assumptions • Simple shading (OpenGL, z-buffering, and Phong illumination model) assumes: – direct illumination (light leaves source, bounces at most once, enters eye) – no shadows – opaque surfaces – point light sources – sometimes fog • (Recursive) ray tracing relaxes those assumptions, simulating: – specular reflection – shadows – transparent surfaces (transmission with refraction) – sometimes indirect illumination (a.k.a. global illumination) – sometimes area light sources – sometimes fog Computer Graphics 15-462 3 Ray Types for Ray Tracing Four ray types: – Eye rays: originate at the eye – Shadow rays: from surface point toward light source – Reflection rays: from surface point in mirror direction – Transmission rays: from surface point in refracted direction Computer Graphics 15-462 4 Ray Tracing Algorithm send ray from eye through each pixel compute point of closest intersection with a scene surface shade that point by computing shadow rays spawn reflected and refracted rays, repeat Computer Graphics 15-462 5 Ray Genealogy EYE Eye Obj3 L1 L2 Obj1 Obj1 Obj2 RAY TREE RAY PATHS (BACKWARD) Computer Graphics 15-462 6 Ray Genealogy EYE Eye Obj3 L1 L1 L2 L2 Obj1 T R Obj2 Obj3 Obj1 Obj2 RAY TREE RAY PATHS (BACKWARD) Computer Graphics 15-462 7 Ray Genealogy EYE Eye Obj3 L1 L1 L2 L2 Obj1 T R L1 L1 Obj2 Obj3 Obj1 L2 L2 R T R X X Obj2 X RAY TREE RAY PATHS (BACKWARD) Computer Graphics 15-462 8 When to stop? EYE Obj3 When a ray leaves the scene L1 L2 When its contribution becomes Obj1 small—at each step the contribution is attenuated by the K’s in the illumination model. -

Chapter 3 Geometrical Optics (A.K.A. Ray Optics
Chapter 3 Geometrical Optics (a.k.a. Ray Optics 3.1 Wavefront Geometrical optics is based on the wave theory of light, and it may be though of a tool that explain the behavior of light, and helps to predict what will happen with light in different situations. It's also the basis of constructing many types of optical devices, such as, e.g., photographic cameras, micro- scopes, telescopes, fiber light guides, and many others. Geometric optics is an extensive field, there is enough material in it to “fill” an entire academic course, even a two-term course. In Ph332, out of necessity, we can only devote to this material three class hours at the mos, so we have to limit ourselves to the most fundamental aspects of this field of optics. As mentioned, geometrical optics is based on the wave theory of light. We have already talked about waves, but only about the most simple ones, propagating in one direction along a single axis. But this is only a special case { in fact, there is a whole lot of other possible situations. A well- known scenario is a circular wave, which can be excited simply by throwing a stone into quiet lake water, as shown, e.g., in this Youtube clip. There are spherical waves { for instance, if an electronic speaker or any other small device generates a sound, the sound propagates in all direction, forming a spherical acoustic wave. In addition to that, the functions describing more complicated waves are 1 no longer as simple as those we used in Chapter 2, namely: 2π 2π ∆y(t) = A sin x − t λ T In the case of a circular wave spreading over a plane (e.g., on the lake surface), we need two coordinates to describe the position on the plane. -

Basic Geometrical Optics
FUNDAMENTALS OF PHOTONICS Module 1.3 Basic Geometrical Optics Leno S. Pedrotti CORD Waco, Texas Optics is the cornerstone of photonics systems and applications. In this module, you will learn about one of the two main divisions of basic optics—geometrical (ray) optics. In the module to follow, you will learn about the other—physical (wave) optics. Geometrical optics will help you understand the basics of light reflection and refraction and the use of simple optical elements such as mirrors, prisms, lenses, and fibers. Physical optics will help you understand the phenomena of light wave interference, diffraction, and polarization; the use of thin film coatings on mirrors to enhance or suppress reflection; and the operation of such devices as gratings and quarter-wave plates. Prerequisites Before you work through this module, you should have completed Module 1-1, Nature and Properties of Light. In addition, you should be able to manipulate and use algebraic formulas, deal with units, understand the geometry of circles and triangles, and use the basic trigonometric functions (sin, cos, tan) as they apply to the relationships of sides and angles in right triangles. 73 Downloaded From: https://www.spiedigitallibrary.org/ebooks on 1/8/2019 DownloadedTerms of Use: From:https://www.spiedigitallibrary.org/terms-of-use http://ebooks.spiedigitallibrary.org/ on 09/18/2013 Terms of Use: http://spiedl.org/terms F UNDAMENTALS OF P HOTONICS Objectives When you finish this module you will be able to: • Distinguish between light rays and light waves. • State the law of reflection and show with appropriate drawings how it applies to light rays at plane and spherical surfaces. -

Chapter 26 Geometrical Optics Chapter 26 Geometrical Optics
Chapter 26 Geometrical Optics Outline 26-1 The Reflection of Light 26-2 Forming Images with a Plane Mirror 26-3 Spherical Mirror 26-4 Ray Tracing and the Mirror Equation 26-5 The Refraction of Light 26-6 Ray Tracing for Lens 26-7ThiL7 Thin Lens Equa tion 26-1 The Reflection of Light Light propagation can be described in terms of “wave front” and “rays”. Wave front is mostly associated with physical optics (difficult to understand), while rays are mostly associated with geometrical optics (easy to understand). Wave front: Think about water wave! Figure 26-1 Wave Fronts and Rays of a point light source • The rays are always traveling in straight line and they indicate the traveling direction of the light--- in Geometrical Optics! • Rays are always at right angle to the wave fronts. More wave fronts Figure 26-2 Spherical (point source light) and Planar (sun light) Wave Fronts In ggpeometrical optics,,y a few rays are used for the representation of the light traveling. The Law of Reflection Figure 26-3 Reflection from a Smooth Surface The Law of Reflection θr = θi The angle of reflection is equal to the angle of incidence (Fig 26-3). The applications of Reflection Law • Reflection on smooth surface (figure a): Specular reflection. • Reflection on rough surface (figure b): Diffuse reflection. Figure 26-4 Reflection from Smooth and Rough Surfaces 26-2 Forming Images with a Plane Mirror Imaging process of the human eye: The imaging process of human is a point – to – point matching process between the distant object and the retina image, in which the image is focused by the eye “lens on the retina for sensing.