Review of Stochastic Differential Equations in Statistical Arbitrage Pairs Trading
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Kadra Gotowa Na Podbój Rio W Numerze
Sylwetki reprezentantów s. 20–69 Numer 2 (22) 2016 ISSN 2391-4807 Kadra gotowa na podbój Rio W NUMERZE Aktualności 4 IGRZYSKA OLIMPIJSKIE RIO 2016 Bardzo mocno trzymam kciuki 6 Rozmowa z ministrem sportu i turystyki Witoldem Bańką Okiem fachowca, czyli na igrzyska jedziemy pełni optymizmu 8 Trenerzy i zawodnicy omawiają szanse Polaków podczas olimpijskich zmagań Brazylijska koncepcja 12 Obiekty olimpijskie w Rio de Janeiro mają służyć sportowcom i mieszkańcom Internet w Rio 12 Przepisy dotyczące korzystania z portali społecznościowych w trakcie IO Mroczne dzielnice, czyli jak przetrwać na igrzyskach 15 Mały poradnik, jak się zachować w przypadku zagrożenia terrorystycznego Telewizja w olimpijskiej formie 16 Minister sportu i turystyki Witold Bańka wierzy Jak obejrzymy igrzyska olimpijskie w TVP w czternaście medali w Rio Tego nie można przegapić w Rio 18 Kto będzie najjaśniejszą gwiazdą igrzysk olimpijskich 2016 6–7 REPREZENTACJA POLSKI GOTOWA DO STARTU W RIO DE JANEIRO Cztery strefy olimpijskie Badminton 22 w Rio gotowe na Boks 23 przyjęcie sportowców Gimnastyka 23 Jeździectwo 23 Judo 24 Kajakarstwo 24 Kolarstwo 27 Lekkoatletyka 30 Łucznictwo 45 Pięciobój nowoczesny 45 12–15 Gry zespołowe: piłka ręczna 46 Gry zespołowe: piłka siatkowa 50 Siatkówka plażowa 52 Pływanie 52 Podnoszenie ciężarów 57 Strzelectwo 58 Szermierka 58 Taekwondo 59 Tenis 60 Tenis stołowy 61 Triatlon 62 Wioślarstwo 62 Zapasy 67 Żeglarstwo 69 Trener musi panować nad NAUKA stresem, żeby nie zawalić Trener musi panować nad stresem, a nie stres nad trenerem 70 70–73 zawodnikowi startu Rozmowa z psychologiem sportu dr. Marcinem Kochanowskim PUBLICYSTYKA Majewskiemu warto w Rio pokibicować 74 felieton Rafała Kazimierczaka Rio – śmiać się czy płakać? 75 felieton Marka Michałowskiego Wydawca: Instytut Sportu w Warszawie ch O Mars na Plutonie, a Polak na podium 76 Koordynator wydawniczy: cz horoskop olimpijski na naszych reprezentantów Piotr Marek Redaktor Naczelny: PARAOLIMPIZM Stefan Tuszyński dorota Dziennikarze: Olgierd Kwiatkowski, . -
0 E Country Event
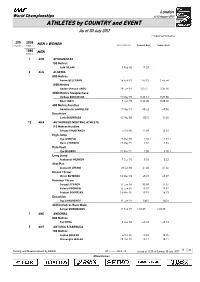
London World Championships 4-13 August 2017 ATHLETES by COUNTRY and EVENT As of 30 July 2017 i = Indoor performance 205 2038 MEN + WOMEN Countries Athletes DATE of BIRTH Personal Best Season Best 1080 MEN Athletes 1 AFG AFGHANISTAN 100 Metres Said GILANI 5 Feb 96 11.33 6 ALG ALGERIA 800 Metres Amine BELFERAR 16 Feb 91 1:45.01 1:45.44 1500 Metres Abderra mane ANOU 29 Jan 91 3:35.2 3:36.50 3000 Metres Steeplec ase Hic am BOUCHICHA 19 May 89 8:20.11 8:27.80 Bilal TABTI 7 Jun 93 8:20.20 8:20.20 400 Metres Hurdles Abdelmali) LAHOULOU 7 May 92 48.62 49.05 Decat lon Larbi BOURRADA 10 May 88 8521 8120 12 ANA AUTHORISED NEUTRAL ATHLETE 110 Metres Hurdles Sergey SHUBEN.O/ 4 Oct 90 12.98 13.01 Hig 0ump Ilya I/AN1U. 9 Mar 93 2.31i 2.31 i Danil L1SEN.O 19 May 97 2.34 2.34 2ole /ault Ilya MUDRO/ 17 Nov 91 5.80 5.70i Long 0ump Ale)sandr MEN.O/ 7 Dec 90 8.56 8.32 S ot 2ut Ale3andr LESNOI 28 Ju 88 21.40 21.36 Discus T row /ictor BUTEN.O 10 Mar 93 65.97 65.07 Hammer T row Serge5 LIT/INO/ 27 Jan 86 80.98 77.32 /aleriy 2RON.IN 15 Jun 94 79.32 79.32 Ale)sei SO.1RS.II 16 Mar 85 78.91 76.23 Decat lon Ilya SH.URENE/ 11 Jan 91 8601 8601 20 .ilometres Race 6al) Sergei SHIROBO.O/ 11 Feb 99 1:18:25 1:18:25 1 AND ANDORRA 800 Metres 2ol MO1A 9 Dec 96 1:48.13 1:48.13 5 ANT ANTIGUA 7 BARBUDA 100 Metres Ce5 ae GREENE 6 Oct 95 10.01 10.05 C a8aug n 6ALSH 29 Dec 87 10.17 10.17 1 Timing and Measurement by SEIKO AT-------.EL3..v1 Issued at 13:33 on Sunday, 30 uly 2017 78 CTTWQWOZDO b\S a London World Championships 4-13 August 2017 ATHLETES by COUNTRY and EVENT DATE of BIRTH -

Iucr Journals
INTERNATIONAL UNION OF Crystallography NEWSLETTER www.iucr.org Volume 21, Number 4 ♦ 2013 APPLY SMART SENSITIVITY CONTROL Confidence means a detector that automatically optimizes its sensitivity for every sample you investigate. Agilent’s new Eos S2, Atlas S2, and Titan S2 CCD detectors employ groundbreaking Smart Sensitivity Control, which maximizes data quality by intelligently tuning detector sensitivity to match the strength of the data observed. Combined with up to 2x faster readout times and instantly switching hardware binning, the S2 range redefines expectations for X-ray diffraction detector performance. Learn how to apply Agilent S2 detectors and Smart Sensitivity Control to your research at www.agilent.com/chem/S2CCD. ACADEMIC & INSTITUTIONAL RESEARCH Agilent is a Proud Global Partner of the International Year of Crystallography Agilent supports a variety of IYCr2014 activities for advancing crystallography worldwide. Learn more at www.agilent.com/chem/iycr2014. © Agilent Technologies, Inc. 2013 LETTER FROM THE PRESIDENT TABLE OF CONTENTS The International Year of Crystallography has arrived after LETTER FROM THE PRESIDENT ..................1 much anticipation and I extend my wishes to all our readers for a fulfilling and productive 2014. This year will re-define IUCR JOURNALS .................................2 our identity as crystallographers and convey our identity to IYCR2014 .....................................4 the world. The IYCr should facilitate good science every- CRYSTALLOGRAPHIC MEETING REPORTS ......9 where and emphasize to youngsters the meaning and reasons for doing science. MILESTONES ...................................22 The opening ceremony of IYCr2014 will be held at the FUTURE MEETINGS ......................22, C4 Gautam R. Desiraju UNESCO headquarters in Paris on 20th and 21st January, NEWS AND NOTICES ..........................23 2014. -

Młodzieżowe Rekordy Polski
stan na: 22.08.2019 MŁODZIE ŻOWE REKORDY POLSKI (U-23) MĘŻ CZY ŹNI 100 m 10.17 Dariusz KU Ć 240486 AZS-AWF Kraków 27.05.2006 Biała Podlaska +1.3 200 m 20.31 Marcin J ĘDRUSI ŃSKI 280981 Olimpia Pozna ń 09.08.2002 Monachium -0.5 400 m 45.35 Marek PLAWGO 250281 KS Warszawianka Warszawa 22.06.2002 Annecy 800 m 1:43.30 Adam KSZCZOT 020989 RKS Łód ź 20.09.2011 Rieti 1000 m 2:16.99 Adam KSZCZOT 020989 RKS Łód ź 31.05.2011 Ostrawa 1500 m 3:36.37 Michał ROZMYS 130395 UKS Barnim Goleniów 05.06.2017 Praga 3000 m 7:50.42 Michał BARTOSZAK 210670 Olimpia Pozna ń 12.09.92 Nuoro 5000m 13:29.72 Michał BARTOSZAK 210670 Olimpia Pozna ń 03.06.92 Victoria 10.000 m 28:30.4 Bronisław MALINOWSKI 040651 Olimpia Grudzi ądz 04.08.73 Celje 3000 m z przeszkodami 8:17.32 Radosław POPŁAWSKI 160183 Astra Nowa Sól 24.08.2004 Ateny 100 m przez płotki 13.29 Tomasz ŚCIGACZEWSKI 181178 KS Warszawianka Warszawa 30.06.99 Oslo +1.5 13.29 Artur NOGA 020588 KS Warszawianka Warszawa 03.07.2010 Eugene +1.6 400 m przez płotki 48.16 Marek PLAWGO 250281 Niestowarzyszony. 12.05.2001 Osaka Skok wzwy ż 2.36 Aleksander WALERIA ŃCZYK 010982 Wawel Kraków 20.07.2003 Bydgoszcz Skok o tyczce 5.91 Paweł WOJCIECHOWSKI 060689 SL WKS Zawisza Bydgoszcz 15.08.2011 Szczecin Skok w dal 8.21 Marcin STARZAK 211085 AZS-AWF Kraków 04.07.2007 Salamanka +1.4 Trójskok 17.11 Jacek PASTUSI ŃSKI 080964 Resovia Rzeszów 17.06.86 Warszawa +1.1 Pchni ęcie kul ą 22.00 h Konrad BUKOWIECKI 170397 KS AZS UWM Olsztyn 15.02.2018 Toru ń Rzut dyskiem 64.74 Piotr MAŁACHOWSKI 070683 WKS Śląsk Wrocław 26.06.2005 Biała Podlaska -

0 E Country Event
London World Championships 4-13 August 2017 ATHLETES by COUNTRY and EVENT As of 30 July 2017 i = Indoor performance 205 2038 MEN + WOMEN Countries Athletes DATE of BIRTH Personal Best Season Best Qualification Best 1080 MEN Athletes 1 AFG AFGHANISTAN 100 Metres 601 Said GILANI 5 Feb 96 11.33 6 ALG ALGERIA 800 Metres 603 Amine BELFERAR 16 Feb 91 1:45.01 1:45.44 1:45.44 1500 Metres 602 Abderrahmane ANOU 29 Jan 91 3:35.2 3:36.50 3:36.50 3000 Metres Steeplechase 604 Hicham BOUCHICHA 19 May 89 8:20.11 8:27.80 8:27.80 607 Bilal TABTI 7 Jun 93 8:20.20 8:20.20 8:20.20 400 Metres Hurdles 606 Abdelmalik LAHOULOU 7 May 92 48.62 49.05 49.05 Decathlon 605 Larbi BOURRADA 10 May 88 8521 8120 8521 12 ANA AUTHORISED NEUTRAL ATHLETE 110 Metres Hurdles 617 Sergey SHUBENKOV 4 Oct 90 12.98 13.01 13.01 High Jump 609 Ilya IVANYUK 9 Mar 93 2.31i 2.31 i 2.31 i 612 Danil LYSENKO 19 May 97 2.34 2.34 2.34 Pole Vault 614 Ilya MUDROV 17 Nov 91 5.80 5.70i 5.70 i Long Jump 613 Aleksandr MENKOV 7 Dec 90 8.56 8.32 8.32 Shot Put 610 Alexandr LESNOI 28 Jul 88 21.40 21.36 21.36 Discus Throw 608 Victor BUTENKO 10 Mar 93 65.97 65.07 65.07 Hammer Throw 611 Sergej LITVINOV 27 Jan 86 80.98 77.32 77.32 615 Valeriy PRONKIN 15 Jun 94 79.32 79.32 78.90 618 Aleksei SOKYRSKII 16 Mar 85 78.91 76.23 76.23 Decathlon 616 Ilya SHKURENEV 11 Jan 91 8601 8601 8601 20 Kilometres Race Walk 350 Sergei SHIROBOKOV 11 Feb 99 1:18:25 1:18:25 1:22:21 1 AND ANDORRA 800 Metres 619 Pol MOYA 9 Dec 96 1:48.13 1:48.13 1:48.13 5 ANT ANTIGUA & BARBUDA 100 Metres 621 Cejhae GREENE 6 Oct 95 10.01 10.05 10.05 -

3000 Metres Steeplechase
12th IAAF World Championships in Athletics Berlin From Saturday 15 August to Sunday 23 August 2009 3000 Metres Steeplechase WOMEN ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHL Final START LIST ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC RESULT NAME NAT AGE DATE VENUE WR8:58.81 Gulnara GALKINA RUS 3017 Aug 2008 Beijing (NS) CR9:06.57 Yekaterina VOLKOVA RUS 2927 Aug 2007 Osaka WL9:09.39 Marta DOMÍNGUEZ ESP 3325 Jul 2009 Barcelona (O) 17 August 2009 20:30 START BIB NAME NAT YEAR PERSONAL BEST 2009 BEST 1 789 Gulnara GALKINA RUS 78 8:58.81 9:11.58 2 602 Ruth Bisibori NYANGAU KEN 88 9:17.35 9:17.85 3 584 Milcah Chemos CHEYWA KEN 86 9:22.33 9:22.33 4 836 Yuliya ZARUDNEVA RUS 86 9:13.18 9:13.18 5 320 Zemzem AHMED ETH 84 9:17.85 9:29.36 6 732 Jessica AUGUSTO POR 81 9:22.50 9:26.64 7 445 Antje MÖLDNER GER 84 9:21.73 9:21.73 8 322 Sofia ASSEFA ETH 87 9:19.91 9:19.91 9 918 Habiba GHRIBI TUN 84 9:24.40 9:24.40 10 300 Eva ARIAS ESP 80 9:25.14 9:25.14 11 968 Jennifer BARRINGER USA 86 9:22.26 9:25.54 12 304 Marta DOMÍNGUEZ ESP 75 9:09.39 9:09.39 13 714 Katarzyna KOWALSKA POL 85 9:26.93 9:26.93 14 352 Sophie DUARTE FRA 81 9:25.62 9:25.62 15 593 Gladys Jerotich KIPKEMOI KEN 86 9:26.03 9:26.03 WORLD TOP ALL-TIME WORLD TOP -

2018 European Championships Statistics – Women’S 3000Msc by K Ken Nakamura
2018 European Championships Statistics – Women’s 3000mSC by K Ken Nakamura Summary: All time performance list at the European Championships Performance Performer Time Name Nat Pos Venue Year 1 1 9:17.57 Yuliya Zarudneva RUS 1 Barcelona 2010 2 2 9:18.85 Gesa -Felicitas Krause GER 1 Amsterdam 2016 3 3 9:26.05 Alesia Turava BLR 1 Göteborg 2006 4 4 9:28.05 Tatyana Petrova RUS 2 Göteborg 2006 5 5 9:28.52 Luiza Gega ALB 2 Amsterdam 2016 6 6 9:29.43 Antje Möldner -Schmidt GER 1 Zürich 2014 7 7 9: 30.16 Charlotta Fougberg SWE 2 Zürich 2014 8 8 9:30.19 Hatti Dean GBR 2 Barcelona 2010 9 9 9:30.70 Diana Martin ESP 3 Zürich 2014 10 10 9:30.99 Svetlana Kudzelich BLR 4 Zürich 2014 Margin of Victory Difference Winning time Name Nat Venue Year Ma x 12.62 9:17.57 Yuliya Zaripova RUS Barcelona 2010 9.67 9:18.85 Gesa-Felicitas Krause GER Amsterdam 2016 2.00 9:26.05 Alesia Turava BLR Göteborg 2006 Min 0.07 9:32.96 Gülcan Mingir TUR Helsinki 2012 Best Marks for Places in the European Championships Pos Time Name Nat Venue Year 1 9:17.57 Yuliya Zarudneva RUS Barcelona 2010 2 9:28.05 Tatyana Petrova RUS Goteborg 2006 3 9:30.70 Diana Martin ESP Zurich 2014 4 9:30.99 Svetlana Kudzelich BLR Zurich 2014 5 9:35.46 Gesa -Felicitas Krause GER Zurich 2014 Fastest non-qualifier for the final Time Position Name Nat Venue Year 9:47.37 5sf1 Roisin McGettigan IRL Göteborg 2006 Multiple Medalists: Antje Möldner-Schmidt: 2012 Bronze; 2014 Gold Wioletta Frankiewicz (POL) 2006 Bronze, 2010 Bronze Multiple Medals by athletes from a single nation Nation Year Gold Silver Bronze -

Impact Analysis of the CAP Reform on Main Agricultural Commodities
Impact analysis of the CAP reform on main agricultural commodities. Report III AGMEMOD – Model Description Lubica Bartova, Robert M’Barek, Hans van Meijl, Myrna van Leeuwen, Andrzej Tabeau, Petra Salamon, Oliver von Ledebur, Frederic Chantreuil, Fabrice Levert, Trevor Donnellan, et al. To cite this version: Lubica Bartova, Robert M’Barek, Hans van Meijl, Myrna van Leeuwen, Andrzej Tabeau, et al.. Impact analysis of the CAP reform on main agricultural commodities. Report III AGMEMOD – Model Description. [Contract] EUR 22940 EN/3, European Commission. 2008, 95 p. hal-01462457 HAL Id: hal-01462457 https://hal.archives-ouvertes.fr/hal-01462457 Submitted on 6 Jun 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Impact Analysis of CAP Reform on the Main Agricultural Commodities Report III AGMEMOD – Model Description Author: AGMEMOD Partnership Editors: Lubica Bartova and Robert M'barek EUR 22940 EN/3 - 2008 The mission of the IPTS is to provide customer-driven support to the EU policy-making process by researching science-based responses to policy challenges that have both a socio-economic as well as a scientific/technological dimension. European Commission Directorate-General Joint Research Centre Institute for Prospective Technological Studies Contact information Address: Edificio Expo. -

All Runners Are Beautiful Mattoni Olomouc HALF MARATHON 15 JUNE 2019
PRESS GUIDE ALL RUNNERS ARE BEAUTIFUL MATTONI OLOMOUC HALF MARATHON 15 JUNE 2019 OLHALF ENG MATTONI OLOMOUC HALF MARATHON PRESS GUIDE INFORMATIONS FOR JOURNALISTS MEDIA CAR Dear Sports Friends, Take advantage of an opportunity to ride in a special car which will drive ahead of the elite runners throughout the race! th Welcome to the 10 edition of the Mattoni Olomouc Half Marathon! • Unique experience • Unrivaled photographs The Press Guide, which you are holding in your hands, contains basic information for journalists about the Mattoni Olomouc • Live coverage from the course Half Marathon. You will also find a short introduction of elite athletes including intermediate times leading to breaking records. We hope you find everything you need to cover this year’s event, but please do not hesitate to ask anyone on the Reserve space in the car at the Press Centre or by calling Bohuslav Stehno at tel: +420 606 044 637. Seating is limited. Press Team, if you need anything else. PRESS TEAM live on ČT SporT Diana Rybachenko Marketing & Communication 777 746 801 [email protected] Bohuslav Stehno PR & Media 606 044 637 [email protected] Matěj Hejda PR & Media 606 044 622 [email protected] PRESS CENTRE #OLhalf The Press Center is a place where media representatives can pick up their credentials. Also, they will find there the latest information about the race, wireless Internet access, live results and live race broadcasting. #OLhalf Friday - Saturday (race day) Conference room of mayor City Hall of Olomouc, Horní Square 583 Opening hours: Friday from 11 am to 8.30 pm City Hall of Olomouc, Conference Room of mayor Saturday from 10 am to 11 pm City Hall of Olomouc, Conference Room of mayor 2 3 MATTONI OLOMOUC HALF MARATHON PRESS GUIDE RACE PROGRAM MEMORIES OF COBBLESTONES AND GLORY. -

Master Schedule.Xlsx
Date Baton Rouge Berlin Morning Time Time Sex Event Round Saturday 8/15 3:05 AM 10:05 M Shot PutQualification Saturday 8/15 3:10 AM 10:10 W 100 Metres Hurdles Heptathlon Saturday 8/15 3:50 AM 10:50 W 3000 Metres Steeplechase Heats Saturday 8/15 4:00 AM 11:00 W Triple Jump Qualification Saturday 8/15 4:20 AM 11:20 W High Jump Heptathlon Saturday 8/15 4:40 AM 11:40 M 100 Metres Heats SaturdaSaturdayy 88/15/15 55:00:00 AM 12:00M Hammer Throw QQualificationualification Saturday 8/15 5:50 AM 12:50 W 400 Metres Heats Saturday 8/15 6:00 AM 13:00 M 20 Kilometres Race Walk Final Saturday 8/15 6:20 AM 13:20 M Hammer ThrowQualification Afternoon session Saturday 8/15 11:15 AM 18:15 M 1500 Metres Heats Saturday 8/15 11:20 AM 18:20 W Shot Put Heptathlon Saturday 8/15 11:50 AM 18:50 M 100 Metres Quarter-Final Saturday 8/15 12:00 PM 19:00 W Pole Vault Qualification Saturday 8/15 12:25 PM 19:25 W 10,000 Metres Final Saturday 8/15 1:15 PM 20:15 M Shot Put Final Saturday 8/15 1:20 PM 20:20 M 400 Metres Hurdles Heats Saturday 8/15 2:10 PM 21:10 W 200 Metres Heptathlon Date Baton Rouge Berlin Date Time Time Morning session Sex Event Round Sunday 8/16 3:05 AM 10:05 W Shot PutQualification Sunday 8/16 3:10 AM 10:10 W 800 Metres Heats Sunday 8/16 3:45 AM 10:45 W Javelin Throw Qualification Sunday 8/16 4:00 AM 11:00 M 3000 Metres Steeplechase Heats Sunday 8/16 4:35 AM 11:35 W Long Jump Heptathlon SundaSundayy 88/16/16 44:55:55 AM 11:11:5555 W 100 Metres Heats Sunday 8/16 5:00 AM 12:00 W 20 Kilometres Race Walk Final Sunday 8/16 5:15 AM 12:15 W Javelin Throw -

International Union of Crystallography Newsletter Volume 20, Number 4 ♦ 2012 Bragg
international union of Crystallography newsletter www.iucr.org Volume 20, Number 4 ♦ 2012 Bragg c e l e B r a t i o 1915 Nobel Prize "For their services in the analysis of crystal structure n by means of X-rays" leTTer from The PresidenT Table of ConTenTs Letter from the President ..................1 The Executive Committee (EC) of the IUCr met iUCr JoUrnaLs .................................2 recently in Adelaide and took some important deci- sions regarding the International Year of Crystallog- editoriaL ........................................5 raphy (IYCr), and our journals. IYCr is going to be a iUCr news .....................................5 very important occasion for all of us to celebrate and CrystaLLograPhiC meeting rePorts ......7 commemorate our subject, to build bridges with the fUtUre meetings .......................22,C4 student community and with the general public at large. I hope that the Year will see a number of new news ...........................................23 country-to-country exchanges and also region-to-re- index to advertisers.......................24 gion ones. Members of the EC have been entrusted CrystaLLograPhiC meetings CaLendar .24 with independent charge of various activities. These Gautam R. Desiraju include regional activities in Africa, Latin America, Editors Eastern and South Eastern Europe and upcoming Judith L. Flippen-Anderson regions in Asia. Planned also are interactions with large facilities and especially the [email protected] SESAME project in the Middle East. IUCr wishes to be actively involved with our Commissions, Regional Associates and National Committees. These activities will William L. Duax be organized and monitored by individual EC members. Educational activities of all [email protected] types will be planned by an individual member. -

The Value of Crowdsourcing for Creative Clusters Development
Acta Innovations ISSN 2300-5599 2016 no. 21: 13-25 13 Bogusław Bembenek Rzeszow University of Technology ul. Powstańców Warszawy 8, 35-959 Rzeszów, [email protected] Katarzyna Kowalska Warsaw School of Economics, UNIMOS pl. Wolności 13, 35-073 Rzeszów, [email protected] THE VALUE OF CROWDSOURCING FOR CREATIVE CLUSTERS DEVELOPMENT Abstract The article consists of three integral parts. It characterises the essence of the functioning of creative clusters, the concept of open innovation and crowdsourcing strategic dimension. Considerations presented in the article are focused on the importance of crowdsourcing in the development of creative clusters. The problem of using crowdsourcing to solve complex problems can be evaluated with multiple levels and multiple perspectives. The authors emphasise that this model of communication between cluster members and external stakeholders allows the use of internal and external resources of creativity in the process of co-creation of positive changes, including innovations (e.g. entrepreneurial solutions to local and global new challenges). They indicate that the implementation of the crowdsourcing in creative clusters can have both, a commercial dimension, where new business projects are the result of the transfer of knowledge, and a non-commercial one, for instance, a wider use of this concept in the development of creative spaces. It was stressed that innovativeness is one of the attributes of entrepreneurial orientation of clusters. Moreover, the key barriers to development of open innovation within a cluster environment are different problems related to intellectual property. The article is based on theoretical research (literature review) and on desk research. Considerations contained herein are conceptual and provide a starting point for further research on the impact of crowdsourcing on the open innovation process within creative clusters.