DOCSLIB.ORG

Advanced Calculus I Fall 2014 §14.7: Local Minima and Maxima

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Advanced Calculus I Fall 2014 §14.7: Local Minima and Maxima Calculus 2502A - Advanced Calculus I Fall 2014 x14.7: Local minima and maxima Martin Frankland November 17, 2014 In these notes, we discuss the problem of finding the local minima and maxima of a function. 1 Background and terminology Definition 1.1. Let f : D ! R be a function, with domain D ⊆ Rn. A point ~a 2 D is called: • a local minimum of f if f(~a) ≤ f(~x) holds for all ~x in some neighborhood of ~a. • a local maximum of f if f(~a) ≥ f(~x) holds for all ~x in some neighborhood of ~a. • a global minimum (or absolute minimum) of f if f(~a) ≤ f(~x) holds for all ~x 2 D. • a global maximum (or absolute maximum) of f if f(~a) ≥ f(~x) holds for all ~x 2 D. An extremum means a minimum or a maximum. Definition 1.2. An interior point ~a 2 D is called a: • critical point of f if f is not differentiable at ~a or if the condition rf(~a) = ~0 holds, i.e., all first-order partial derivatives of f are zero at ~a. • saddle point of f if it is a critical point which is not a local extremum. In other words, for every neighborhood U of ~a, there is some point ~x 2 U satisfying f(~x) < f(~a) and some point ~x 2 U satisfying f(~x) > f(~a). Remark 1.3. Global minima or maxima are not necessarily unique. For example, the function f : R ! R defined by f(x) = sin x has a global maximum with value 1 at the points: 3π π 5π nπ o :::; − ; ; ;::: = + 2kπ j k 2 2 2 2 2 Z 1 and a global minimum with value −1 at the points: π 3π 7π 3π :::; − ; ; ;::: = + 2kπ j k 2 : 2 2 2 2 Z For a sillier example, consider a constant function g(~x) = c for all ~x 2 D. Then every point ~x 2 D is simultaneously a global minimum and a global maximum of g. Proposition 1.4. Let ~a be an interior point of the domain D. If ~a is a local extremum of f, then any partial derivative of f which exists at ~a must be zero. Proof. Assume that the partial derivative Dmf(~a) exists, for some 1 ≤ m ≤ n. Then the function of a single variable mth coordinate z}|{ g(x) := f(a1; a2;:::; x ; : : : ; an−1; an) is differentiable at x = am and has a local extremum at x = am. Therefore its derivative vanishes at that point: 0 g (am) = Dmf(~a) = 0: Remark 1.5. The converse does not hold: a critical point of f need not be a local extremum. For example, the function f(x) = x3 has a critical point at x = 0 which is a saddle point. Upshot: In order to find the local extrema of f, it suffices to consider the critical points of f. 2 2 One-dimensional case Recall the second derivative test from single variable calculus. Proposition 2.1 (Second derivative test). Let f : D ! R be a function of a single variable, with domain D ⊆ R. Let a 2 D be a critical point of f such that the first derivative f 0 exists in a neighborhood of a, and the second derivative f 00(a) exists. • If f 00(a) > 0 holds, then f has a local minimum at a. • If f 00(a) < 0 holds, then f has a local maximum at a. • If f 00(a) = 0 holds, then the test is inconclusive. Remark 2.2. The following examples illustrate why the test is inconclusive when the critical point a satisfies f 00(a) = 0. • The function f(x) = x4 has a local minimum at 0. • The function f(x) = −x4 has a local maximum at 0. • The function f(x) = x3 has a saddle point at 0. Example 2.3. Find all local extrema of the function f : R ! R defined by f(x) = 3x4 − 4x3 − 12x2 + 10: Solution. Note that f is twice differentiable on all of R, and moreover the domain of f is open in R (so that there are no boundary points to check). Let us find the critical points of f: f 0(x) = 12x3 − 12x2 − 24x = 0 , x3 − x2 − 2x = 0 , x x2 − x − 2 = 0 , x(x + 1)(x − 2) = 0 , x = −1; 0; or 2: Let us use the second derivative test to classify these critical points: f 00(x) = 12 3x2 − 2x − 2 f 00(−1) = 12 (3 + 2 − 2) = 12(3) > 0 f 00(0) = 12 (−2) < 0 f 00(2) = 12 (12 − 4 − 2) = 12(6) > 0 from which we conclude: 3 • x = −1 is a local minimum of f, with value f(−1) = 3 + 4 − 12 + 10 = 5 . • x = 0 is a local maximum of f, with value f(0) = 10 . • x = 2 is a local minimum of f, with value f(2) = 3(16) − 4(8) − 12(4) + 10 = −22 . Remark 2.4. In this example, the function f has no global maximum, because it grows arbi- trarily large: limx!+1 f(x) = +1. Moreover, the condition limx→−∞ f(x) = +1, together with the extreme value theorem, implies that f reaches a global minimum. Therefore, x = 2 is in fact the global minimum of f, with value f(2) = −22, as illustrated in Figure 1. 40 f(x) 20 x −2 −1 1 2 3 −20 Figure 1: Graph of the function f in Example 2.3. 4 3 Two-dimensional case Theorem 3.1 (Second derivatives test). Let f : D ! R be a function of two variables, with domain D ⊆ R2. Let (a; b) 2 D be a critical point of f such that the second partial derivatives fxx, fxy, fyx, fyy exist in a neighborhood of (a; b) and are continuous at (a; b), which implies in particular fxy(a; b) = fyx(a; b). The discriminant of f is the 2 × 2 determinant fxx fxy D := fyx fyy 2 = fxxfyy − fxy: Now consider the discriminant D = D(a; b) at the point (a; b). • If D > 0 and fxx(a; b) > 0 hold, then f has a local minimum at (a; b). • If D > 0 and fxx(a; b) < 0 hold, then f has a local maximum at (a; b). • If D < 0 holds, then f has a saddle point at (a; b). • If D = 0 holds, then the test is inconclusive. Remark 3.2. The following examples illustrate why the test is inconclusive when the discrim- inant satisfies D = 0 . • The function f(x; y) = x2 + y4 has a (strict) local minimum at (0; 0). • The function f(x; y) = x2 has a (non-strict) local minimum at (0; 0). • The function f(x; y) = −x2 − y4 has a (strict) local maximum at (0; 0). • The function f(x; y) = −x2 has a (non-strict) local maximum at (0; 0). • The function f(x; y) = x2 + y3 has a saddle point at (0; 0). • The function f(x; y) = −x2 + y3 has a saddle point at (0; 0). • The function f(x; y) = x2 − y4 has a saddle point at (0; 0). Example 3.3 (# 14.7.11). Find all local extrema and saddle points of the function f : R2 ! R defined by f(x; y) = x3 − 12xy + 8y3: 5 Solution. Note that f is infinitely many times differentiable on its domain R2. Let us find the critical points of f: ( 2 fx(x; y) = 3x − 12y = 0 2 fy(x; y) = −12x + 24y = 0 ( 4y = x2 , x = 2y2 ) 4y = (2y2)2 = 4y4 , y = y4 , y(y3 − 1) = 0 , y = 0 or y3 = 1 , y = 0 or y = 1 y = 0 ) x = 2(0)2 = 0 y = 1 ) x = 2(1)2 = 2 which implies that (0; 0) and (2; 1) are the only points that could be critical points of f, and indeed they are. Let us compute the discriminant of f: fxx(x; y) = 6x fxy(x; y) = −12 fyy(x; y) = 48y 2 D(x; y) = fxx(x; y)fyy(x; y) − fxy(x; y) = (6x)(48y) − (−12)2 = 122 (2xy − 1) : At the critical point (0; 0), the discriminant is: D(0; 0) = 122(0 − 1) < 0 so that (0; 0) is a saddle point . At the critical point (2; 1), the discriminant is: D(2; 1) = 122(4 − 1) > 0 and we have fxx(2; 1) = 6(2) = 12 > 0, so that (2; 1) is a local minimum with value f(2; 1) = 8 − 24 + 8 = −8 , as illustrated in Figure 2.. 6 500 0 z −500 4 2 −4 0 −2 0 −2 2 4 y x −4 Figure 2: Graph of the function f in Example 3.3. 4 Why does it work? 4.1 Quadratic approximation The second derivatives test relies on the quadratic approximation of f at the point (a; b), which is the Taylor polynomial of degree 2 at that point. Recall that for functions of a single variable f(x), the quadratic approximation of f at a is: (x − a)2 f(x) ≈ f(a) + f 0(a)(x − a) + f 00(a) : 2 Since the variable of interest is the displacement from the basepoint a, let us rewrite h := x−a and thus: h2 f(a + h) ≈ f(a) + f 0(a)h + f 00(a) : 2 If a is a critical point of f, then we have f 0(a) = 0 and the quadratic approximation becomes: h2 f(a + h) ≈ f(a) + f 00(a) : 2 If f 00(a) 6= 0 holds, then the quadratic term will determine the local behavior of f around a: f 00(a) > 0 yields a local minimum while f 00(a) < 0 yields a local maximum.
Load more

Recommended publications
  • Math 2374: Multivariable Calculus and Vector Analysis
    Math 2374: Multivariable Calculus and Vector Analysis Part 25 Fall 2012 Extreme points Definition If f : U ⊂ Rn ! R is a scalar function, • a point x0 2 U is called a local minimum of f if there is a neighborhood V of x0 such that for all points x 2 V, f (x) ≥ f (x0), • a point x0 2 U is called a local maximum of f if there is a neighborhood V of x0 such that for all points x 2 V, f (x) ≤ f (x0), • a point x0 2 U is called a local, or relative, extremum of f if it is either a local minimum or a local maximum, • a point x0 2 U is called a critical point of f if either f is not differentiable at x0 or if rf (x0) = Df (x0) = 0, • a critical point that is not a local extremum is called a saddle point. First Derivative Test for Local Extremum Theorem If U ⊂ Rn is open, the function f : U ⊂ Rn ! R is differentiable, and x0 2 U is a local extremum, then Df (x0) = 0; that is, x0 is a critical point. Proof. Suppose that f achieves a local maximum at x0, then for all n h 2 R , the function g(t) = f (x0 + th) has a local maximum at t = 0. Thus from one-variable calculus g0(0) = 0. By chain rule 0 g (0) = [Df (x0)] h = 0 8h So Df (x0) = 0. Same proof for a local minimum. Examples Ex-1 Find the maxima and minima of the function f (x; y) = x2 + y 2.
    [Show full text]
  • A Stability Boundary Based Method for Finding Saddle Points on Potential Energy Surfaces
    JOURNAL OF COMPUTATIONAL BIOLOGY Volume 13, Number 3, 2006 © Mary Ann Liebert, Inc. Pp. 745–766 A Stability Boundary Based Method for Finding Saddle Points on Potential Energy Surfaces CHANDAN K. REDDY and HSIAO-DONG CHIANG ABSTRACT The task of finding saddle points on potential energy surfaces plays a crucial role in under- standing the dynamics of a micromolecule as well as in studying the folding pathways of macromolecules like proteins. The problem of finding the saddle points on a high dimen- sional potential energy surface is transformed into the problem of finding decomposition points of its corresponding nonlinear dynamical system. This paper introduces a new method based on TRUST-TECH (TRansformation Under STability reTained Equilibria CHaracter- ization) to compute saddle points on potential energy surfaces using stability boundaries. Our method explores the dynamic and geometric characteristics of stability boundaries of a nonlinear dynamical system. A novel trajectory adjustment procedure is used to trace the stability boundary. Our method was successful in finding the saddle points on different potential energy surfaces of various dimensions. A simplified version of the algorithm has also been used to find the saddle points of symmetric systems with the help of some analyt- ical knowledge. The main advantages and effectiveness of the method are clearly illustrated with some examples. Promising results of our method are shown on various problems with varied degrees of freedom. Key words: potential energy surfaces, saddle points, stability boundary, minimum gradient point, computational chemistry. I. INTRODUCTION ecently, there has been a lot of interest across various disciplines to understand a wide Rvariety of problems related to bioinformatics.
    [Show full text]
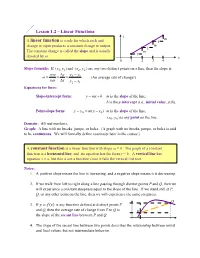
  • Lesson 1.2 – Linear Functions Y M a Linear Function Is a Rule for Which Each Unit 1 Change in Input Produces a Constant Change in Output
    Lesson 1.2 – Linear Functions y m A linear function is a rule for which each unit 1 change in input produces a constant change in output. m 1 The constant change is called the slope and is usually m 1 denoted by m. x 0 1 2 3 4 Slope formula: If (x1, y1)and (x2 , y2 ) are any two distinct points on a line, then the slope is rise y y y m 2 1 . (An average rate of change!) run x x x 2 1 Equations for lines: Slope-intercept form: y mx b m is the slope of the line; b is the y-intercept (i.e., initial value, y(0)). Point-slope form: y y0 m(x x0 ) m is the slope of the line; (x0, y0 ) is any point on the line. Domain: All real numbers. Graph: A line with no breaks, jumps, or holes. (A graph with no breaks, jumps, or holes is said to be continuous. We will formally define continuity later in the course.) A constant function is a linear function with slope m = 0. The graph of a constant function is a horizontal line, and its equation has the form y = b. A vertical line has equation x = a, but this is not a function since it fails the vertical line test. Notes: 1. A positive slope means the line is increasing, and a negative slope means it is decreasing. 2. If we walk from left to right along a line passing through distinct points P and Q, then we will experience a constant steepness equal to the slope of the line.
    [Show full text]
  • 3.2 Sources, Sinks, Saddles, and Spirals
    3.2. Sources, Sinks, Saddles, and Spirals 161 3.2 Sources, Sinks, Saddles, and Spirals The pictures in this section show solutions to Ay00 By0 Cy 0. These are linear equations with constant coefficients A; B; and C .C The graphsC showD solutions y on the horizontal axis and their slopes y0 dy=dt on the vertical axis. These pairs .y.t/;y0.t// depend on time, but time is not inD the pictures. The paths show where the solution goes, but they don’t show when. Each specific solution starts at a particular point .y.0/;y0.0// given by the initial conditions. The point moves along its path as the time t moves forward from t 0. D We know that the solutions to Ay00 By0 Cy 0 depend on the two solutions to 2 C C D As Bs C 0 (an ordinary quadratic equation for s). When we find the roots s1 and C C D s2, we have found all possible solutions : s1t s2t s1t s2t y c1e c2e y c1s1e c2s2e (1) D C 0 D C The numbers s1 and s2 tell us which picture we are in. Then the numbers c1 and c2 tell us which path we are on. Since s1 and s2 determine the picture for each equation, it is essential to see the six possibilities. We write all six here in one place, to compare them. Later they will appear in six different places, one with each figure. The first three have real solutions s1 and s2. The last three have complex pairs s a i!.
    [Show full text]
  • Lecture 8: Maxima and Minima
    Maxima and minima Lecture 8: Maxima and Minima Rafikul Alam Department of Mathematics IIT Guwahati Rafikul Alam IITG: MA-102 (2013) Maxima and minima Local extremum of f : Rn ! R Let f : U ⊂ Rn ! R be continuous, where U is open. Then • f has a local maximum at p if there exists r > 0 such that f (x) ≤ f (p) for x 2 B(p; r): • f has a local minimum at a if there exists > 0 such that f (x) ≥ f (p) for x 2 B(p; ): A local maximum or a local minimum is called a local extremum. Rafikul Alam IITG: MA-102 (2013) Maxima and minima Figure: Local extremum of z = f (x; y) Rafikul Alam IITG: MA-102 (2013) Maxima and minima Necessary condition for extremum of Rn ! R Critical point: A point p 2 U is a critical point of f if rf (p) = 0: Thus, when f is differentiable, the tangent plane to z = f (x) at (p; f (p)) is horizontal. Theorem: Suppose that f has a local extremum at p and that rf (p) exists. Then p is a critical point of f , i.e, rf (p) = 0: 2 2 Example: Consider f (x; y) = x − y : Then fx = 2x = 0 and fy = −2y = 0 show that (0; 0) is the only critical point of f : But (0; 0) is not a local extremum of f : Rafikul Alam IITG: MA-102 (2013) Maxima and minima Saddle point Saddle point: A critical point of f that is not a local extremum is called a saddle point of f : Examples: 2 2 • The point (0; 0) is a saddle point of f (x; y) = x − y : 2 2 2 • Consider f (x; y) = x y + y x: Then fx = 2xy + y = 0 2 and fy = 2xy + x = 0 show that (0; 0) is the only critical point of f : But (0; 0) is a saddle point.
    [Show full text]
  • Calculus and Differential Equations II
    Calculus and Differential Equations II MATH 250 B Linear systems of differential equations Linear systems of differential equations Calculus and Differential Equations II Second order autonomous linear systems We are mostly interested with2 × 2 first order autonomous systems of the form x0 = a x + b y y 0 = c x + d y where x and y are functions of t and a, b, c, and d are real constants. Such a system may be re-written in matrix form as d x x a b = M ; M = : dt y y c d The purpose of this section is to classify the dynamics of the solutions of the above system, in terms of the properties of the matrix M. Linear systems of differential equations Calculus and Differential Equations II Existence and uniqueness (general statement) Consider a linear system of the form dY = M(t)Y + F (t); dt where Y and F (t) are n × 1 column vectors, and M(t) is an n × n matrix whose entries may depend on t. Existence and uniqueness theorem: If the entries of the matrix M(t) and of the vector F (t) are continuous on some open interval I containing t0, then the initial value problem dY = M(t)Y + F (t); Y (t ) = Y dt 0 0 has a unique solution on I . In particular, this means that trajectories in the phase space do not cross. Linear systems of differential equations Calculus and Differential Equations II General solution The general solution to Y 0 = M(t)Y + F (t) reads Y (t) = C1 Y1(t) + C2 Y2(t) + ··· + Cn Yn(t) + Yp(t); = U(t) C + Yp(t); where 0 Yp(t) is a particular solution to Y = M(t)Y + F (t).
    [Show full text]
  • Maxima, Minima, and Saddle Points
    Real Analysis III (MAT312β) Department of Mathematics University of Ruhuna A.W.L. Pubudu Thilan Department of Mathematics University of Ruhuna | Real Analysis III(MAT312β) 1/80 Chapter 12 Maxima, Minima, and Saddle Points Department of Mathematics University of Ruhuna | Real Analysis III(MAT312β) 2/80 Introduction A scientist or engineer will be interested in the ups and downs of a function, its maximum and minimum values, its turning points. For instance, locating extreme values is the basic objective of optimization. In the simplest case, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. Department of Mathematics University of Ruhuna | Real Analysis III(MAT312β) 3/80 Introduction Cont... Drawing a graph of a function using a computer graph plotting package will reveal behavior of the function. But if we want to know the precise location of maximum and minimum points, we need to turn to algebra and differential calculus. In this Chapter we look at how we can find maximum and minimum points in this way. Department of Mathematics University of Ruhuna | Real Analysis III(MAT312β) 4/80 Chapter 12 Section 12.1 Single Variable Functions Department of Mathematics University of Ruhuna | Real Analysis III(MAT312β) 5/80 Local maximum and local minimum The local maximum and local minimum (plural: maxima and minima) of a function, are the largest and smallest value that the function takes at a point within a given interval. It may not be the minimum or maximum for the whole function, but locally it is.
    [Show full text]
  • 9 Power and Polynomial Functions
    Arkansas Tech University MATH 2243: Business Calculus Dr. Marcel B. Finan 9 Power and Polynomial Functions A function f(x) is a power function of x if there is a constant k such that f(x) = kxn If n > 0, then we say that f(x) is proportional to the nth power of x: If n < 0 then f(x) is said to be inversely proportional to the nth power of x. We call k the constant of proportionality. Example 9.1 (a) The strength, S, of a beam is proportional to the square of its thickness, h: Write a formula for S in terms of h: (b) The gravitational force, F; between two bodies is inversely proportional to the square of the distance d between them. Write a formula for F in terms of d: Solution. 2 k (a) S = kh ; where k > 0: (b) F = d2 ; k > 0: A power function f(x) = kxn , with n a positive integer, is called a mono- mial function. A polynomial function is a sum of several monomial func- tions. Typically, a polynomial function is a function of the form n n−1 f(x) = anx + an−1x + ··· + a1x + a0; an 6= 0 where an; an−1; ··· ; a1; a0 are all real numbers, called the coefficients of f(x): The number n is a non-negative integer. It is called the degree of the polynomial. A polynomial of degree zero is just a constant function. A polynomial of degree one is a linear function, of degree two a quadratic function, etc. The number an is called the leading coefficient and a0 is called the constant term.
    [Show full text]
  • Polynomials.Pdf
    POLYNOMIALS James T. Smith San Francisco State University For any real coefficients a0,a1,...,an with n $ 0 and an =' 0, the function p defined by setting n p(x) = a0 + a1 x + AAA + an x for all real x is called a real polynomial of degree n. Often, we write n = degree p and call an its leading coefficient. The constant function with value zero is regarded as a real polynomial of degree –1. For each n the set of all polynomials with degree # n is closed under addition, subtraction, and multiplication by scalars. The algebra of polynomials of degree # 0 —the constant functions—is the same as that of real num- bers, and you need not distinguish between those concepts. Polynomials of degrees 1 and 2 are called linear and quadratic. Polynomial multiplication Suppose f and g are nonzero polynomials of degrees m and n: m f (x) = a0 + a1 x + AAA + am x & am =' 0, n g(x) = b0 + b1 x + AAA + bn x & bn =' 0. Their product fg is a nonzero polynomial of degree m + n: m+n f (x) g(x) = a 0 b 0 + AAA + a m bn x & a m bn =' 0. From this you can deduce the cancellation law: if f, g, and h are polynomials, f =' 0, and fg = f h, then g = h. For then you have 0 = fg – f h = f ( g – h), hence g – h = 0. Note the analogy between this wording of the cancellation law and the corresponding fact about multiplication of numbers. One of the most useful results about integer multiplication is the unique factoriza- tion theorem: for every integer f > 1 there exist primes p1 ,..., pm and integers e1 em e1 ,...,em > 0 such that f = pp1 " m ; the set consisting of all pairs <pk , ek > is unique.
    [Show full text]
  • Analysis of Asymptotic Escape of Strict Saddle Sets in Manifold Optimization
    Analysis of Asymptotic Escape of Strict Saddle Sets in Manifold Optimization Thomas Y. Hou∗ , Zhenzhen Li y , and Ziyun Zhang z Abstract. In this paper, we provide some analysis on the asymptotic escape of strict saddles in manifold optimization using the projected gradient descent (PGD) algorithm. One of our main contributions is that we extend the current analysis to include non-isolated and possibly continuous saddle sets with complicated geometry. We prove that the PGD is able to escape strict critical submanifolds under certain conditions on the geometry and the distribution of the saddle point sets. We also show that the PGD may fail to escape strict saddles under weaker assumptions even if the saddle point set has zero measure and there is a uniform escape direction. We provide a counterexample to illustrate this important point. We apply this saddle analysis to the phase retrieval problem on the low-rank matrix manifold, prove that there are only a finite number of saddles, and they are strict saddles with high probability. We also show the potential application of our analysis for a broader range of manifold optimization problems. Key words. Manifold optimization, projected gradient descent, strict saddles, stable manifold theorem, phase retrieval AMS subject classifications. 58D17, 37D10, 65F10, 90C26 1. Introduction. Manifold optimization has long been studied in mathematics. From signal and imaging science [38][7][36], to computer vision [47][48] and quantum informa- tion [40][16][29], it finds applications in various disciplines.
    [Show full text]
  • Instability Analysis of Saddle Points by a Local Minimax Method
    INSTABILITY ANALYSIS OF SADDLE POINTS BY A LOCAL MINIMAX METHOD JIANXIN ZHOU Abstract. The objective of this work is to develop some tools for local insta- bility analysis of multiple critical points, which can be computationally carried out. The Morse index can be used to measure local instability of a nondegen- erate saddle point. However, it is very expensive to compute numerically and is ineffective for degenerate critical points. A local (weak) linking index can also be defined to measure local instability of a (degenerate) saddle point. But it is still too difficult to compute. In this paper, a local instability index, called a local minimax index, is defined by using a local minimax method. This new instability index is known beforehand and can help in finding a saddle point numerically. Relations between the local minimax index and other local insta- bility indices are established. Those relations also provide ways to numerically compute the Morse, local linking indices. In particular, the local minimax index can be used to define a local instability index of a saddle point relative to a reference (trivial) critical point even in a Banach space while others failed to do so. 1. Introduction Multiple solutions with different performance, maneuverability and instability in- dices exist in many nonlinear problems in natural or social sciences [1,7, 9,24,29,31, 33,35]. When cases are variational, the problems reduce to solving the Euler- Lagrange equation (1.1) J 0(u) = 0; where J is a C1 generic energy functional on a Banach space H and J 0 its Frechet derivative.
    [Show full text]
  • Gradient Descent Can Take Exponential Time to Escape Saddle Points
    Gradient Descent Can Take Exponential Time to Escape Saddle Points Simon S. Du Chi Jin Carnegie Mellon University University of California, Berkeley [email protected] [email protected] Jason D. Lee Michael I. Jordan University of Southern California University of California, Berkeley [email protected] [email protected] Barnabás Póczos Aarti Singh Carnegie Mellon University Carnegie Mellon University [email protected] [email protected] Abstract Although gradient descent (GD) almost always escapes saddle points asymptot- ically [Lee et al., 2016], this paper shows that even with fairly natural random initialization schemes and non-pathological functions, GD can be significantly slowed down by saddle points, taking exponential time to escape. On the other hand, gradient descent with perturbations [Ge et al., 2015, Jin et al., 2017] is not slowed down by saddle points—it canfind an approximate local minimizer in polynomial time. This result implies that GD is inherently slower than perturbed GD, and justifies the importance of adding perturbations for efficient non-convex optimization. While our focus is theoretical, we also present experiments that illustrate our theoreticalfindings. 1 Introduction Gradient Descent (GD) and its myriad variants provide the core optimization methodology in machine learning problems. Given a functionf(x), the basic GD method can be written as: x(t+1) x (t) η f x(t) , (1) ← − ∇ where η is a step size, assumedfixed in the current paper.� While� precise characterizations of the rate of convergence GD are available for convex problems, there is far less understanding of GD for non-convex problems. Indeed, for general non-convex problems, GD is only known tofind a stationary point (i.e., a point where the gradient equals zero) in polynomial time [Nesterov, 2013].
    [Show full text]