Mode-Finding for Mixtures of Gaussian Distributions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

5. the Student T Distribution
Virtual Laboratories > 4. Special Distributions > 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 5. The Student t Distribution In this section we will study a distribution that has special importance in statistics. In particular, this distribution will arise in the study of a standardized version of the sample mean when the underlying distribution is normal. The Probability Density Function Suppose that Z has the standard normal distribution, V has the chi-squared distribution with n degrees of freedom, and that Z and V are independent. Let Z T= √V/n In the following exercise, you will show that T has probability density function given by −(n +1) /2 Γ((n + 1) / 2) t2 f(t)= 1 + , t∈ℝ ( n ) √n π Γ(n / 2) 1. Show that T has the given probability density function by using the following steps. n a. Show first that the conditional distribution of T given V=v is normal with mean 0 a nd variance v . b. Use (a) to find the joint probability density function of (T,V). c. Integrate the joint probability density function in (b) with respect to v to find the probability density function of T. The distribution of T is known as the Student t distribution with n degree of freedom. The distribution is well defined for any n > 0, but in practice, only positive integer values of n are of interest. This distribution was first studied by William Gosset, who published under the pseudonym Student. In addition to supplying the proof, Exercise 1 provides a good way of thinking of the t distribution: the t distribution arises when the variance of a mean 0 normal distribution is randomized in a certain way. -

Chapter 8 Fundamental Sampling Distributions And
CHAPTER 8 FUNDAMENTAL SAMPLING DISTRIBUTIONS AND DATA DESCRIPTIONS 8.1 Random Sampling pling procedure, it is desirable to choose a random sample in the sense that the observations are made The basic idea of the statistical inference is that we independently and at random. are allowed to draw inferences or conclusions about a Random Sample population based on the statistics computed from the sample data so that we could infer something about Let X1;X2;:::;Xn be n independent random variables, the parameters and obtain more information about the each having the same probability distribution f (x). population. Thus we must make sure that the samples Define X1;X2;:::;Xn to be a random sample of size must be good representatives of the population and n from the population f (x) and write its joint proba- pay attention on the sampling bias and variability to bility distribution as ensure the validity of statistical inference. f (x1;x2;:::;xn) = f (x1) f (x2) f (xn): ··· 8.2 Some Important Statistics It is important to measure the center and the variabil- ity of the population. For the purpose of the inference, we study the following measures regarding to the cen- ter and the variability. 8.2.1 Location Measures of a Sample The most commonly used statistics for measuring the center of a set of data, arranged in order of mag- nitude, are the sample mean, sample median, and sample mode. Let X1;X2;:::;Xn represent n random variables. Sample Mean To calculate the average, or mean, add all values, then Bias divide by the number of individuals. -

A Tail Quantile Approximation Formula for the Student T and the Symmetric Generalized Hyperbolic Distribution
A Service of Leibniz-Informationszentrum econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible. zbw for Economics Schlüter, Stephan; Fischer, Matthias J. Working Paper A tail quantile approximation formula for the student t and the symmetric generalized hyperbolic distribution IWQW Discussion Papers, No. 05/2009 Provided in Cooperation with: Friedrich-Alexander University Erlangen-Nuremberg, Institute for Economics Suggested Citation: Schlüter, Stephan; Fischer, Matthias J. (2009) : A tail quantile approximation formula for the student t and the symmetric generalized hyperbolic distribution, IWQW Discussion Papers, No. 05/2009, Friedrich-Alexander-Universität Erlangen-Nürnberg, Institut für Wirtschaftspolitik und Quantitative Wirtschaftsforschung (IWQW), Nürnberg This Version is available at: http://hdl.handle.net/10419/29554 Standard-Nutzungsbedingungen: Terms of use: Die Dokumente auf EconStor dürfen zu eigenen wissenschaftlichen Documents in EconStor may be saved and copied for your Zwecken und zum Privatgebrauch gespeichert und kopiert werden. personal and scholarly purposes. Sie dürfen die Dokumente nicht für öffentliche oder kommerzielle You are not to copy documents for public or commercial Zwecke vervielfältigen, öffentlich ausstellen, öffentlich zugänglich purposes, to exhibit the documents publicly, to make them machen, vertreiben oder anderweitig nutzen. publicly available on the internet, or to distribute or otherwise use the documents in public. Sofern die Verfasser die Dokumente unter Open-Content-Lizenzen (insbesondere CC-Lizenzen) zur Verfügung gestellt haben sollten, If the documents have been made available under an Open gelten abweichend von diesen Nutzungsbedingungen die in der dort Content Licence (especially Creative Commons Licences), you genannten Lizenz gewährten Nutzungsrechte. may exercise further usage rights as specified in the indicated licence. www.econstor.eu IWQW Institut für Wirtschaftspolitik und Quantitative Wirtschaftsforschung Diskussionspapier Discussion Papers No. -

Chapter 4: Central Tendency and Dispersion
Central Tendency and Dispersion 4 In this chapter, you can learn • how the values of the cases on a single variable can be summarized using measures of central tendency and measures of dispersion; • how the central tendency can be described using statistics such as the mode, median, and mean; • how the dispersion of scores on a variable can be described using statistics such as a percent distribution, minimum, maximum, range, and standard deviation along with a few others; and • how a variable’s level of measurement determines what measures of central tendency and dispersion to use. Schooling, Politics, and Life After Death Once again, we will use some questions about 1980 GSS young adults as opportunities to explain and demonstrate the statistics introduced in the chapter: • Among the 1980 GSS young adults, are there both believers and nonbelievers in a life after death? Which is the more common view? • On a seven-attribute political party allegiance variable anchored at one end by “strong Democrat” and at the other by “strong Republican,” what was the most Democratic attribute used by any of the 1980 GSS young adults? The most Republican attribute? If we put all 1980 95 96 PART II :: DESCRIPTIVE STATISTICS GSS young adults in order from the strongest Democrat to the strongest Republican, what is the political party affiliation of the person in the middle? • What was the average number of years of schooling completed at the time of the survey by 1980 GSS young adults? Were most of these twentysomethings pretty close to the average on -
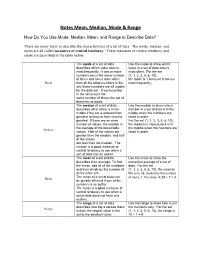
Notes Mean, Median, Mode & Range
Notes Mean, Median, Mode & Range How Do You Use Mode, Median, Mean, and Range to Describe Data? There are many ways to describe the characteristics of a set of data. The mode, median, and mean are all called measures of central tendency. These measures of central tendency and range are described in the table below. The mode of a set of data Use the mode to show which describes which value occurs value in a set of data occurs most frequently. If two or more most often. For the set numbers occur the same number {1, 1, 2, 3, 5, 6, 10}, of times and occur more often the mode is 1 because it occurs Mode than all the other numbers in the most frequently. set, those numbers are all modes for the data set. If each number in the set occurs the same number of times, the set of data has no mode. The median of a set of data Use the median to show which describes what value is in the number in a set of data is in the middle if the set is ordered from middle when the numbers are greatest to least or from least to listed in order. greatest. If there are an even For the set {1, 1, 2, 3, 5, 6, 10}, number of values, the median is the median is 3 because it is in the average of the two middle the middle when the numbers are Median values. Half of the values are listed in order. greater than the median, and half of the values are less than the median. -

Mixture Random Effect Model Based Meta-Analysis for Medical Data
Mixture Random Effect Model Based Meta-analysis For Medical Data Mining Yinglong Xia?, Shifeng Weng?, Changshui Zhang??, and Shao Li State Key Laboratory of Intelligent Technology and Systems,Department of Automation, Tsinghua University, Beijing, China [email protected], [email protected], fzcs,[email protected] Abstract. As a powerful tool for summarizing the distributed medi- cal information, Meta-analysis has played an important role in medical research in the past decades. In this paper, a more general statistical model for meta-analysis is proposed to integrate heterogeneous medi- cal researches efficiently. The novel model, named mixture random effect model (MREM), is constructed by Gaussian Mixture Model (GMM) and unifies the existing fixed effect model and random effect model. The pa- rameters of the proposed model are estimated by Markov Chain Monte Carlo (MCMC) method. Not only can MREM discover underlying struc- ture and intrinsic heterogeneity of meta datasets, but also can imply reasonable subgroup division. These merits embody the significance of our methods for heterogeneity assessment. Both simulation results and experiments on real medical datasets demonstrate the performance of the proposed model. 1 Introduction As the great improvement of experimental technologies, the growth of the vol- ume of scientific data relevant to medical experiment researches is getting more and more massively. However, often the results spreading over journals and on- line database appear inconsistent or even contradict because of variance of the studies. It makes the evaluation of those studies to be difficult. Meta-analysis is statistical technique for assembling to integrate the findings of a large collection of analysis results from individual studies. -

A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess
S S symmetry Article A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess Guillermo Martínez-Flórez 1, Víctor Leiva 2,* , Emilio Gómez-Déniz 3 and Carolina Marchant 4 1 Departamento de Matemáticas y Estadística, Facultad de Ciencias Básicas, Universidad de Córdoba, Montería 14014, Colombia; [email protected] 2 Escuela de Ingeniería Industrial, Pontificia Universidad Católica de Valparaíso, 2362807 Valparaíso, Chile 3 Facultad de Economía, Empresa y Turismo, Universidad de Las Palmas de Gran Canaria and TIDES Institute, 35001 Canarias, Spain; [email protected] 4 Facultad de Ciencias Básicas, Universidad Católica del Maule, 3466706 Talca, Chile; [email protected] * Correspondence: [email protected] or [email protected] Received: 30 June 2020; Accepted: 19 August 2020; Published: 1 September 2020 Abstract: In this paper, we consider skew-normal distributions for constructing new a distribution which allows us to model proportions and rates with zero/one inflation as an alternative to the inflated beta distributions. The new distribution is a mixture between a Bernoulli distribution for explaining the zero/one excess and a censored skew-normal distribution for the continuous variable. The maximum likelihood method is used for parameter estimation. Observed and expected Fisher information matrices are derived to conduct likelihood-based inference in this new type skew-normal distribution. Given the flexibility of the new distributions, we are able to show, in real data scenarios, the good performance of our proposal. Keywords: beta distribution; centered skew-normal distribution; maximum-likelihood methods; Monte Carlo simulations; proportions; R software; rates; zero/one inflated data 1. -

D. Normal Mixture Models and Elliptical Models
D. Normal Mixture Models and Elliptical Models 1. Normal Variance Mixtures 2. Normal Mean-Variance Mixtures 3. Spherical Distributions 4. Elliptical Distributions QRM 2010 74 D1. Multivariate Normal Mixture Distributions Pros of Multivariate Normal Distribution • inference is \well known" and estimation is \easy". • distribution is given by µ and Σ. • linear combinations are normal (! VaR and ES calcs easy). • conditional distributions are normal. > • For (X1;X2) ∼ N2(µ; Σ), ρ(X1;X2) = 0 () X1 and X2 are independent: QRM 2010 75 Multivariate Normal Variance Mixtures Cons of Multivariate Normal Distribution • tails are thin, meaning that extreme values are scarce in the normal model. • joint extremes in the multivariate model are also too scarce. • the distribution has a strong form of symmetry, called elliptical symmetry. How to repair the drawbacks of the multivariate normal model? QRM 2010 76 Multivariate Normal Variance Mixtures The random vector X has a (multivariate) normal variance mixture distribution if d p X = µ + WAZ; (1) where • Z ∼ Nk(0;Ik); • W ≥ 0 is a scalar random variable which is independent of Z; and • A 2 Rd×k and µ 2 Rd are a matrix and a vector of constants, respectively. > Set Σ := AA . Observe: XjW = w ∼ Nd(µ; wΣ). QRM 2010 77 Multivariate Normal Variance Mixtures Assumption: rank(A)= d ≤ k, so Σ is a positive definite matrix. If E(W ) < 1 then easy calculations give E(X) = µ and cov(X) = E(W )Σ: We call µ the location vector or mean vector and we call Σ the dispersion matrix. The correlation matrices of X and AZ are identical: corr(X) = corr(AZ): Multivariate normal variance mixtures provide the most useful examples of elliptical distributions. -

Mixture Modeling with Applications in Alzheimer's Disease
University of Kentucky UKnowledge Theses and Dissertations--Epidemiology and Biostatistics College of Public Health 2017 MIXTURE MODELING WITH APPLICATIONS IN ALZHEIMER'S DISEASE Frank Appiah University of Kentucky, [email protected] Digital Object Identifier: https://doi.org/10.13023/ETD.2017.100 Right click to open a feedback form in a new tab to let us know how this document benefits ou.y Recommended Citation Appiah, Frank, "MIXTURE MODELING WITH APPLICATIONS IN ALZHEIMER'S DISEASE" (2017). Theses and Dissertations--Epidemiology and Biostatistics. 14. https://uknowledge.uky.edu/epb_etds/14 This Doctoral Dissertation is brought to you for free and open access by the College of Public Health at UKnowledge. It has been accepted for inclusion in Theses and Dissertations--Epidemiology and Biostatistics by an authorized administrator of UKnowledge. For more information, please contact [email protected]. STUDENT AGREEMENT: I represent that my thesis or dissertation and abstract are my original work. Proper attribution has been given to all outside sources. I understand that I am solely responsible for obtaining any needed copyright permissions. I have obtained needed written permission statement(s) from the owner(s) of each third-party copyrighted matter to be included in my work, allowing electronic distribution (if such use is not permitted by the fair use doctrine) which will be submitted to UKnowledge as Additional File. I hereby grant to The University of Kentucky and its agents the irrevocable, non-exclusive, and royalty-free license to archive and make accessible my work in whole or in part in all forms of media, now or hereafter known. -

Volatility Modeling Using the Student's T Distribution
Volatility Modeling Using the Student’s t Distribution Maria S. Heracleous Dissertation submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Economics Aris Spanos, Chair Richard Ashley Raman Kumar Anya McGuirk Dennis Yang August 29, 2003 Blacksburg, Virginia Keywords: Student’s t Distribution, Multivariate GARCH, VAR, Exchange Rates Copyright 2003, Maria S. Heracleous Volatility Modeling Using the Student’s t Distribution Maria S. Heracleous (ABSTRACT) Over the last twenty years or so the Dynamic Volatility literature has produced a wealth of uni- variateandmultivariateGARCHtypemodels.Whiletheunivariatemodelshavebeenrelatively successful in empirical studies, they suffer from a number of weaknesses, such as unverifiable param- eter restrictions, existence of moment conditions and the retention of Normality. These problems are naturally more acute in the multivariate GARCH type models, which in addition have the problem of overparameterization. This dissertation uses the Student’s t distribution and follows the Probabilistic Reduction (PR) methodology to modify and extend the univariate and multivariate volatility models viewed as alternative to the GARCH models. Its most important advantage is that it gives rise to internally consistent statistical models that do not require ad hoc parameter restrictions unlike the GARCH formulations. Chapters 1 and 2 provide an overview of my dissertation and recent developments in the volatil- ity literature. In Chapter 3 we provide an empirical illustration of the PR approach for modeling univariate volatility. Estimation results suggest that the Student’s t AR model is a parsimonious and statistically adequate representation of exchange rate returns and Dow Jones returns data. -

The Value at the Mode in Multivariate T Distributions: a Curiosity Or Not?
The value at the mode in multivariate t distributions: a curiosity or not? Christophe Ley and Anouk Neven Universit´eLibre de Bruxelles, ECARES and D´epartement de Math´ematique,Campus Plaine, boulevard du Triomphe, CP210, B-1050, Brussels, Belgium Universit´edu Luxembourg, UR en math´ematiques,Campus Kirchberg, 6, rue Richard Coudenhove-Kalergi, L-1359, Luxembourg, Grand-Duchy of Luxembourg e-mail: [email protected]; [email protected] Abstract: It is a well-known fact that multivariate Student t distributions converge to multivariate Gaussian distributions as the number of degrees of freedom ν tends to infinity, irrespective of the dimension k ≥ 1. In particular, the Student's value at the mode (that is, the normalizing ν+k Γ( 2 ) constant obtained by evaluating the density at the center) cν;k = k=2 ν converges towards (πν) Γ( 2 ) the Gaussian value at the mode c = 1 . In this note, we prove a curious fact: c tends k (2π)k=2 ν;k monotonically to ck for each k, but the monotonicity changes from increasing in dimension k = 1 to decreasing in dimensions k ≥ 3 whilst being constant in dimension k = 2. A brief discussion raises the question whether this a priori curious finding is a curiosity, in fine. AMS 2000 subject classifications: Primary 62E10; secondary 60E05. Keywords and phrases: Gamma function, Gaussian distribution, value at the mode, Student t distribution, tail weight. 1. Foreword. One of the first things we learn about Student t distributions is the fact that, when the degrees of freedom ν tend to infinity, we retrieve the Gaussian distribution, which has the lightest tails in the Student family of distributions. -

Statistics, Measures of Central Tendency I
Statistics, Measures of Central TendencyI We are considering a random variable X with a probability distribution which has some parameters. We want to get an idea what these parameters are. We perfom an experiment n times and record the outcome. This means we have X1;:::; Xn i.i.d. random variables, with probability distribution same as X . We want to use the outcome to infer what the parameters are. Mean The outcomes are x1;:::; xn. The Sample Mean is x1+···+xn x := n . Also sometimes called the average. The expected value of X , EX , is also called the mean of X . Often denoted by µ. Sometimes called population mean. Median The number so that half the values are below, half above. If the sample is of even size, you take the average of the middle terms. Mode The number that occurs most frequently. There could be several modes, or no mode. Dan Barbasch Math 1105 Chapter 9 Week of September 25 1 / 24 Statistics, Measures of Central TendencyII Example You have a coin for which you know that P(H) = p and P(T ) = 1 − p: You would like to estimate p. You toss it n times. You count the number of heads. The sample mean should be an estimate of p: EX = p, and E(X1 + ··· + Xn) = np: So X + ··· + X E 1 n = p: n Dan Barbasch Math 1105 Chapter 9 Week of September 25 2 / 24 Descriptive StatisticsI Frequency Distribution Divide into a number of equal disjoint intervals. For each interval count the number of elements in the sample occuring.