MASTER T H E S I S Automatic Detection of Hindustani Talas
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Music Initiative Jka Peer - Reviewed Journal of Music
VOL. 01 NO. 01 APRIL 2018 MUSIC INITIATIVE JKA PEER - REVIEWED JOURNAL OF MUSIC PUBLISHED,PRINTED & OWNED BY HIGHER EDUCATION DEPARTMENT, J&K CIVIL SECRETARIAT, JAMMU/SRINAGAR,J&K CONTACT NO.S: 01912542880,01942506062 www.jkhighereducation.nic.in EDITOR DR. ASGAR HASSAN SAMOON (IAS) PRINCIPAL SECRETARY HIGHER EDUCATION GOVT. OF JAMMU & KASHMIR YOOR HIGHER EDUCATION,J&K NOT FOR SALE COVER DESIGN: NAUSHAD H GA JK MUSIC INITIATIVE A PEER - REVIEWED JOURNAL OF MUSIC INSTRUCTION TO CONTRIBUTORS A soft copy of the manuscript should be submitted to the Editor of the journal in Microsoft Word le format. All the manuscripts will be blindly reviewed and published after referee's comments and nally after Editor's acceptance. To avoid delay in publication process, the papers will not be sent back to the corresponding author for proof reading. It is therefore the responsibility of the authors to send good quality papers in strict compliance with the journal guidelines. JK Music Initiative is a quarterly publication of MANUSCRIPT GUIDELINES Higher Education Department, Authors preparing submissions are asked to read and follow these guidelines strictly: Govt. of Jammu and Kashmir (JKHED). Length All manuscripts published herein represent Research papers should be between 3000- 6000 words long including notes, bibliography and captions to the opinion of the authors and do not reect the ofcial policy illustrations. Manuscripts must be typed in double space throughout including abstract, text, references, tables, and gures. of JKHED or institution with which the authors are afliated unless this is clearly specied. Individual authors Format are responsible for the originality and genuineness of the work Documents should be produced in MS Word, using a single font for text and headings, left hand justication only and no embedded formatting of capitals, spacing etc. -

1 Syllabus for MA (Previous) Hindustani Music Vocal/Instrumental
Syllabus for M.A. (Previous) Hindustani Music Vocal/Instrumental (Sitar, Sarod, Guitar, Violin, Santoor) SEMESTER-I Core Course – 1 Theory Credit - 4 Theory : 70 Internal Assessment : 30 Maximum Marks : 100 Historical and Theoretical Study of Ragas 70 Marks A. Historical Study of the following Ragas from the period of Sangeet Ratnakar onwards to modern times i) Gaul/Gaud iv) Kanhada ii) Bhairav v) Malhar iii) Bilawal vi) Todi B. Development of Raga Classification system in Ancient, Medieval and Modern times. C. Study of the following Ragangas in the modern context:- Sarang, Malhar, Kanhada, Bhairav, Bilawal, Kalyan, Todi. D. Detailed and comparative study of the Ragas prescribed in Appendix – I Internal Assessment 30 marks Core Course – 2 Theory Credit - 4 Theory : 70 Internal Assessment : 30 Maximum Marks : 100 Music of the Asian Continent 70 Marks A. Study of the Music of the following - China, Arabia, Persia, South East Asia, with special reference to: i) Origin, development and historical background of Music ii) Musical scales iii) Important Musical Instruments B. A comparative study of the music systems mentioned above with Indian Music. Internal Assessment 30 marks Core Course – 3 Practical Credit - 8 Practical : 70 Internal Assessment : 30 Maximum Marks : 100 Stage Performance 70 marks Performance of half an hour’s duration before an audience in Ragas selected from the list of Ragas prescribed in Appendix – I Candidate may plan his/her performance in the following manner:- Classical Vocal Music i) Khyal - Bada & chota Khyal with elaborations for Vocal Music. Tarana is optional. Classical Instrumental Music ii) Alap, Jor, Jhala, Masitkhani and Razakhani Gat with eleaborations Semi Classical Music iii) A short piece of classical music /Thumri / Bhajan/ Dhun /a gat in a tala other than teentaal may also be presented. -

Famous Indian Classical Musicians and Vocalists Free Static GK E-Book
oliveboard FREE eBooks FAMOUS INDIAN CLASSICAL MUSICIANS & VOCALISTS For All Banking and Government Exams Famous Indian Classical Musicians and Vocalists Free static GK e-book Current Affairs and General Awareness section is one of the most important and high scoring sections of any competitive exam like SBI PO, SSC-CGL, IBPS Clerk, IBPS SO, etc. Therefore, we regularly provide you with Free Static GK and Current Affairs related E-books for your preparation. In this section, questions related to Famous Indian Classical Musicians and Vocalists have been asked. Hence it becomes very important for all the candidates to be aware about all the Famous Indian Classical Musicians and Vocalists. In all the Bank and Government exams, every mark counts and even 1 mark can be the difference between success and failure. Therefore, to help you get these important marks we have created a Free E-book on Famous Indian Classical Musicians and Vocalists. The list of all the Famous Indian Classical Musicians and Vocalists is given in the following pages of this Free E-book on Famous Indian Classical Musicians and Vocalists. Sample Questions - Q. Ustad Allah Rakha played which of the following Musical Instrument? (a) Sitar (b) Sarod (c) Surbahar (d) Tabla Answer: Option D – Tabla Q. L. Subramaniam is famous for playing _________. (a) Saxophone (b) Violin (c) Mridangam (d) Flute Answer: Option B – Violin Famous Indian Classical Musicians and Vocalists Free static GK e-book Famous Indian Classical Musicians and Vocalists. Name Instrument Music Style Hindustani -
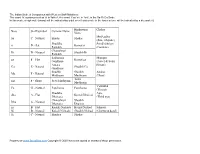
Note Staff Symbol Carnatic Name Hindustani Name Chakra Sa C
The Indian Scale & Comparison with Western Staff Notations: The vowel 'a' is pronounced as 'a' in 'father', the vowel 'i' as 'ee' in 'feet', in the Sa-Ri-Ga Scale In this scale, a high note (swara) will be indicated by a dot over it and a note in the lower octave will be indicated by a dot under it. Hindustani Chakra Note Staff Symbol Carnatic Name Name MulAadhar Sa C - Natural Shadaj Shadaj (Base of spine) Shuddha Swadhishthan ri D - flat Komal ri Rishabh (Genitals) Chatushruti Ri D - Natural Shudhh Ri Rishabh Sadharana Manipur ga E - Flat Komal ga Gandhara (Navel & Solar Antara Plexus) Ga E - Natural Shudhh Ga Gandhara Shudhh Shudhh Anahat Ma F - Natural Madhyam Madhyam (Heart) Tivra ma F - Sharp Prati Madhyam Madhyam Vishudhh Pa G - Natural Panchama Panchama (Throat) Shuddha Ajna dha A - Flat Komal Dhaivat Dhaivata (Third eye) Chatushruti Shudhh Dha A - Natural Dhaivata Dhaivat ni B - Flat Kaisiki Nishada Komal Nishad Sahsaar Ni B - Natural Kakali Nishada Shudhh Nishad (Crown of head) Så C - Natural Shadaja Shadaj Property of www.SarodSitar.com Copyright © 2010 Not to be copied or shared without permission. Short description of Few Popular Raags :: Sanskrut (Sanskrit) pronunciation is Raag and NOT Raga (Alphabetical) Aroha Timing Name of Raag (Karnataki Details Avroha Resemblance) Mood Vadi, Samvadi (Main Swaras) It is a old raag obtained by the combination of two raags, Ahiri Sa ri Ga Ma Pa Ga Ma Dha ni Så Ahir Bhairav Morning & Bhairav. It belongs to the Bhairav Thaat. Its first part (poorvang) has the Bhairav ang and the second part has kafi or Så ni Dha Pa Ma Ga ri Sa (Chakravaka) serious, devotional harpriya ang. -

And Joydeep Ghosh (Sarod)
The Asian Indian Classical Music Society 51491 Norwich Drive Granger, IN 46530 Concert Announcement Vidushi Mita Nag (sitar) Pandit Joydeep Ghosh (sarod) with Pandit Subhen Chatterjee (Tabla) April 26, 2016, Tuesday, 7.00PM At: the Andrews Auditorium, Geddes Hall University of Notre Dame Cosponsored with the Liu Institute of Asia and Asian Studies Tickets available at gate. General Admission: $10, AICMS Members and ND/SMC faculty: $5, Students: FREE Mita Nag, daughter of the veteran sitarist, Pandit Manilal Nag and granddaughter of Sangeet Acharya Gokul Nag, belongs to the Vishnupur Gharana of Bengal, a school of music that is nearly 300 years old and which is known for its dhrupad style of playing. She was initiated into music at the age of four, and studied with her mother, grandfather and father. She appeared for her debut performance at the age of ten, when she also won the Government of India’s Junior National Talent Search Award. She has given many concert performances, both alone and with her father, in cities in the US, Canada, Japan and Europe as well as in India. Joydeep Ghosh is hailed as one of India’s leading sarod, surshringar and Mohanveena artists. He started his sarod training at the age of five, and has studied with the great masters the late Sangeetacharya Anil Roychoudhury , late Sangeetacharya Radhika Mohan Moitra and Padmabhusan Acharya Buddhadev Dasgupta all of the Shahajahanpur Gharana. He has won numerous awards and fellowships, including those from the Government of India, the title of “Suramani” from the Sur Singar Samsad (Mumbai) and “Swarshree” from Swarankur (Mumbai). -

Teachers of Private Colleges (Under Section 17 – Elected Members (6) of the Kerala University Act, 1974)
1 Price Rs. 100/- per copy UNIVERSITY OF KERALA Election to the Senate from the Teachers of Private Colleges (Under Section 17 – Elected Members (6) of the Kerala University Act, 1974) ELECTORAL ROLL OF TEACHERS OF PRIVATE COLLEGES-2018 ROLL No. Name Designation College 1. Dr.Caroline Beena Mendez DDO All Saints’ College. 2. Sonya J Nair Assistant Professor ,, 3. Kukku Xavier Assistant Professor ,, 4. Dr.Liji Varghese Assistant Professor ,, 5. Dr.Sr.Pascoela Adelrich Assistant Professor ,, D’Souza 6. Dr.Rajsree M.S Assistant Professor ,, 7. Sapna Srinivas Assistant Professor ,, 8. Simna S Stephen Assistant Professor ,, 9. Nishel Prem Elias Assistant Professor ,, 10. Diana V Prakash Assistant Professor ,, 11. Dr.Kavitha .N Assistant Professor ,, 12. Joveeta Justin Assistant Professor ,, 13. Celina James Assistant Professor ,, 14. Dr.C.Udayakala Assistant Professor ,, 15. Parvathy Menon Assistant Professor ,, 16. Vijayakumari K Assistant Professor ,, 17. Dr.Sreelekha Nair Associate professor ,, 18. Dr.Reshmi.R.Prasad Associate professor ,, 19. Lissy Bennet Assistant Professor ,, 20. Shirly Joseph Associate professor All Saints’ College. 21. Sebina Mathew C Assistant Professor ,, 22. Renjini Raveendran P Assistant Professor ,, 23. Vidhya T.R Assistant Professor ,, 24. Dr.Deepa M Associate professor ,, 25. Dr.Anjana P.S Assistant Professor ,, 2 26. Dr.Veena Suresh Babu Assistant Professor ,, 27. Dr.Sunitha Kurur Assistant Professor ,, 28. Dr.Sindhu Yesodharan Assistant Professor ,, 29. Dr.Siji V.L Assistant Professor ,, 30. Dr.Beena Kumari K.S Assistant Professor ,, 31. Dr.Nisha K.K Assistant Professor ,, 32. Dr.Sr.Shaina T J Assistant Professor ,, 33. Dr.Dhanalekshmi.T.G Assistant Professor ,, 34. Divya Grace Dilip Assistant Professor ,, 35. -
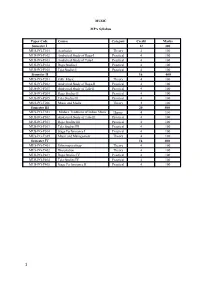
MUSIC MPA Syllabus Paper Code Course Category Credit Marks
MUSIC MPA Syllabus Paper Code Course Category Credit Marks Semester I 12 300 MUS-PG-T101 Aesthetics Theory 4 100 MUS-PG-P102 Analytical Study of Raga-I Practical 4 100 MUS-PG-P103 Analytical Study of Tala-I Practical 4 100 MUS-PG-P104 Raga Studies I Practical 4 100 MUS-PG-P105 Tala Studies I Practical 4 100 Semester II 16 400 MUS-PG-T201 Folk Music Theory 4 100 MUS-PG-P202 Analytical Study of Raga-II Practical 4 100 MUS-PG-P203 Analytical Study of Tala-II Practical 4 100 MUS-PG-P204 Raga Studies II Practical 4 100 MUS-PG-P205 Tala Studies II Practical 4 100 MUS-PG-T206 Music and Media Theory 4 100 Semester III 20 500 MUS-PG-T301 Modern Traditions of Indian Music Theory 4 100 MUS-PG-P302 Analytical Study of Tala-III Practical 4 100 MUS-PG-P303 Raga Studies III Practical 4 100 MUS-PG-P303 Tala Studies III Practical 4 100 MUS-PG-P304 Stage Performance I Practical 4 100 MUS-PG-T305 Music and Management Theory 4 100 Semester IV 16 400 MUS-PG-T401 Ethnomusicology Theory 4 100 MUS-PG-T402 Dissertation Theory 4 100 MUS-PG-P403 Raga Studies IV Practical 4 100 MUS-PG-P404 Tala Studies IV Practical 4 100 MUS-PG-P405 Stage Performance II Practical 4 100 1 Semester I MUS-PG-CT101:- Aesthetic Course Detail- The course will primarily provide an overview of music and allied issues like Aesthetics. The discussions will range from Rasa and its varieties [According to Bharat, Abhinavagupta, and others], thoughts of Rabindranath Tagore and Abanindranath Tagore on music to aesthetics and general comparative. -

Signatory ID Name CIN Company Name 02700003 RAM TIKA
Signatory ID Name CIN Company Name 02700003 RAM TIKA U55101DL1998PTC094457 RVS HOTELS AND RESORTS 02700032 BANSAL SHYAM SUNDER U70102AP2005PTC047718 SHREEMUKH PROPERTIES PRIVATE 02700065 CHHIBA SAVITA U01100MH2004PTC150274 DEJA VU FARMS PRIVATE LIMITED 02700070 PARATE VIJAYKUMAR U45200MH1993PTC072352 PARATE DEVELOPERS P LTD 02700076 BHARATI GHOSH U85110WB2007PTC118976 ACCURATE MEDICARE & 02700087 JAIN MANISH RAJMAL U45202MH1950PTC008342 LEO ESTATES PRIVATE LIMITED 02700109 NATESAN RAMACHANDRAN U51505TN2002PTC049271 RESHMA ELECTRIC PRIVATE 02700110 JEGADEESAN MAHENDRAN U51505TN2002PTC049271 RESHMA ELECTRIC PRIVATE 02700126 GUPTA JAGDISH PRASAD U74210MP2003PTC015880 GOPAL SEVA PRIVATE LIMITED 02700155 KRISHNAKUMARAN NAIR U45201GJ1994PTC021976 SHARVIL HOUSING PVT LTD 02700157 DHIREN OZA VASANTLAL U45201GJ1994PTC021976 SHARVIL HOUSING PVT LTD 02700183 GUPTA KEDAR NATH U72200AP2004PTC044434 TRAVASH SOFTWARE SOLUTIONS 02700187 KUMARASWAMY KUNIGAL U93090KA2006PLC039899 EMERALD AIRLINES LIMITED 02700216 JAIN MANOJ U15400MP2007PTC020151 CHAMBAL VALLEY AGRO 02700222 BHAIYA SHARAD U45402TN1996PTC036292 NORTHERN TANCHEM PRIVATE 02700226 HENDIN URI ZIPORI U55101HP2008PTC030910 INNER WELLSPRING HOSPITALITY 02700266 KUMARI POLURU VIJAYA U60221PY2001PLC001594 REGENCY TRANSPORT CARRIERS 02700285 DEVADASON NALLATHAMPI U72200TN2006PTC059044 ZENTERE SOLUTIONS PRIVATE 02700322 GOPAL KAKA RAM U01400UP2007PTC033194 KESHRI AGRI GENETICS PRIVATE 02700342 ASHISH OBERAI U74120DL2008PTC184837 ASTHA LAND SCAPE PRIVATE 02700354 MADHUSUDHANA REDDY U70200KA2005PTC036400 -

New and Bestselling Titles Sociology 2016-2017
New and Bestselling titles Sociology 2016-2017 www.sagepub.in Sociology | 2016-17 Seconds with Alice W Clark How is this book helpful for young women of Any memorable experience that you hadhadw whilehile rural areas with career aspirations? writing this book? Many rural families are now keeping their girls Becoming part of the Women’s Studies program in school longer, and this book encourages at Allahabad University; sharing in the colourful page 27A these families to see real benefit for themselves student and faculty life of SNDT University in supporting career development for their in Mumbai; living in Vadodara again after daughters. It contributes in this way by many years, enjoying friends and colleagues; identifying the individual roles that can be played reconnecting with friendships made in by supportive fathers and mothers, even those Bangalore. Being given entrée to lively students with very little education themselves. by professors who cared greatly about them. Being treated wonderfully by my interviewees. What facets of this book bring-in international Any particular advice that you would like to readership? share with young women aiming for a successful Views of women’s striving for self-identity career? through professionalism; the factors motivating For women not yet in college: Find supporters and encouraging them or setting barriers to their in your family to help argue your case to those accomplishments. who aren’t so supportive. Often it’s submissive Upward trends in women’s education, the and dutiful mothers who need a prompt from narrowing of the gender gap, and the effects a relative with a broader viewpoint. -

Sl No Localbody Name Ward No Door No Sub No Resident Name Address Mobile No Type of Damage Unique Number Status Rejection Remarks
Flood 2019 - Vythiri Taluk Sl No Localbody Name Ward No Door No Sub No Resident Name Address Mobile No Type of Damage Unique Number Status Rejection Remarks 1 Kalpetta Municipality 1 0 kamala neduelam 8157916492 No damage 31219021600235 Approved(Disbursement) RATION CARD DETAILS NOT AVAILABLE 2 Kalpetta Municipality 1 135 sabitha strange nivas 8086336019 No damage 31219021600240 Disbursed to Government 3 Kalpetta Municipality 1 138 manjusha sukrutham nedunilam 7902821756 No damage 31219021600076 Pending THE ADHAR CARD UPDATED ANOTHER ACCOUNT 4 Kalpetta Municipality 1 144 devi krishnan kottachira colony 9526684873 No damage 31219021600129 Verified(LRC Office) NO BRANCH NAME AND IFSC CODE 5 Kalpetta Municipality 1 149 janakiyamma kozhatatta 9495478641 >75% Damage 31219021600080 Verified(LRC Office) PASSBOOK IS NO CLEAR 6 Kalpetta Municipality 1 151 anandavalli kozhathatta 9656336368 No damage 31219021600061 Disbursed to Government 7 Kalpetta Municipality 1 16 chandran nedunilam st colony 9747347814 No damage 31219021600190 Withheld PASSBOOK NOT CLEAR 8 Kalpetta Municipality 1 16 3 sangeetha pradeepan rajasree gives nedunelam 9656256950 No damage 31219021600090 Withheld No damage type details and damage photos 9 Kalpetta Municipality 1 161 shylaja sasneham nedunilam 9349625411 No damage 31219021600074 Disbursed to Government Manjusha padikkandi house 10 Kalpetta Municipality 1 172 3 maniyancode padikkandi house maniyancode 9656467963 16 - 29% Damage 31219021600072 Disbursed to Government 11 Kalpetta Municipality 1 175 vinod madakkunnu colony -

Musical Explorers Is Made Available to a Nationwide Audience Through Carnegie Hall’S Weill Music Institute
Weill Music Institute Teacher Musical Guide Explorers My City, My Song A Program of the Weill Music Institute at Carnegie Hall for Students in Grades K–2 2016 | 2017 Weill Music Institute Teacher Musical Guide Explorers My City, My Song A Program of the Weill Music Institute at Carnegie Hall for Students in Grades K–2 2016 | 2017 WEILL MUSIC INSTITUTE Joanna Massey, Director, School Programs Amy Mereson, Assistant Director, Elementary School Programs Rigdzin Pema Collins, Coordinator, Elementary School Programs Tom Werring, Administrative Assistant, School Programs ADDITIONAL CONTRIBUTERS Michael Daves Qian Yi Alsarah Nahid Abunama-Elgadi Etienne Charles Teni Apelian Yeraz Markarian Anaïs Tekerian Reph Starr Patty Dukes Shanna Lesniak Savannah Music Festival PUBLISHING AND CREATIVE SERVICES Carol Ann Cheung, Senior Editor Eric Lubarsky, Senior Editor Raphael Davison, Senior Graphic Designer ILLUSTRATIONS Sophie Hogarth AUDIO PRODUCTION Jeff Cook Weill Music Institute at Carnegie Hall 881 Seventh Avenue | New York, NY 10019 Phone: 212-903-9670 | Fax: 212-903-0758 [email protected] carnegiehall.org/MusicalExplorers Musical Explorers is made available to a nationwide audience through Carnegie Hall’s Weill Music Institute. Lead funding for Musical Explorers has been provided by Ralph W. and Leona Kern. Major funding for Musical Explorers has been provided by the E.H.A. Foundation and The Walt Disney Company. © Additional support has been provided by the Ella Fitzgerald Charitable Foundation, The Lanie & Ethel Foundation, and -

1457621917.Pdf
ATN DD BHARATI Schedule MAR 07 TO MAR 13,2016 ET Monday Tuesday Wednesday Thursday Friday Saturday Sunday PT 7-Mar 8-Mar 9-Mar 10-Mar 11-Mar 12-Mar 13-Mar Asian Magazine Asian Magazine Asian Magazine Utsav Asian Magazine Asian Magazine Asian Magazine Asian Magazine 0:00 Ryerson University Holi Celebration Unity Festival 21:00 Konkani Association SMCC Youth Talent Show Taal Se Taal Mila Ek Shaam Kishore Kumar Ke Naam Shafqat Amanat Ali Live in Mississauga Part 01 Markham Part 01 Asian Magazine Asian Magazine Utsav Asian Magazine Asian Magazine Asian Magazine Asian Magazine Asian Magazine 0:30 Ryerson University Holi Celebration 21:30 Konkani Association Sunehri Yaadein Sham - E- Parag Canada's Diversity Celebration Rung : South Asian Heritage Weekend Toronto Festival of Literature & Arts Part 02 Part 02 1:00 Yog Vigyan Yog Vigyan Yog Vigyan Yog Vigyan Yog Vigyan Yog Vigyan Yog Vigyan 22:00 1:30 Thin Green Line Nano Ki Duniya Nano Ki Duniya Nano Ki Duniya Nano Ki Duniya Nano Ki Duniya Nano Ki Duniya 22:30 2:00 K Sankar Pillai Muzaffar Ali Ashq Dur Se Nazdeek Se A.K. Roychoudhary Ramakrishna Paramahamsa Spirit of soul DST 23:00 2:30 Sankat Mochan Hanuman Sankat Mochan Hanuman Sankat Mochan Hanuman Sankat Mochan Hanuman Sankat Mochan Hanuman Sankat Mochan Hanuman DST 23:30 3:00 Women of Substance Bandhan Bandhan Bandhan Bandhan Bhisham Sahani 0:00 Bandhan 3:30 Sanskriti Bharati Rang Tarang Aas Paas Sanskriti Bharati Sanskriti Bharati Sanskriti Bharati 0:30 4:00 Kitabnama Maati Ke Rang - Chaho To Pa Lo Kanya Kumari Ki Kahaniya : Mangal Sutra Kanya Kumari Ki Kahaniya 1:00 Bharat ke Sant Kavi ABhImanyu's Face Best of Indian Cinema :Vazhakku- Tamil Sarvjan Prarthanalay Chandani Chowk Chandani Chowk Chandani Chowk 4:30 Chandani Chowk Chandani Chowk 1:30 5:00 2:00 Carnatic Vocal : Dr.