DOCSLIB.ORG

Optimal Resource Allocation Model to Prevent, Prepare, and Respond to Multiple Disruptions, with Application to the Deepwater Horizon Oil Spill and Hurricane Katrina

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Optimal Resource Allocation Model to Prevent, Prepare, and Respond to Multiple Disruptions, with Application to the Deepwater Horizon Oil Spill and Hurricane Katrina Industrial and Manufacturing Systems Industrial and Manufacturing Systems Engineering Publications Engineering 1-28-2021 Optimal Resource Allocation Model to Prevent, Prepare, and Respond to Multiple Disruptions, with Application to the Deepwater Horizon Oil Spill and Hurricane Katrina Cameron A. MacKenzie Iowa State University, [email protected] Amro Al Kazimi Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/imse_pubs Part of the Operational Research Commons, Risk Analysis Commons, and the Systems Engineering Commons The complete bibliographic information for this item can be found at https://lib.dr.iastate.edu/ imse_pubs/261. For information on how to cite this item, please visit http://lib.dr.iastate.edu/ howtocite.html. This Book Chapter is brought to you for free and open access by the Industrial and Manufacturing Systems Engineering at Iowa State University Digital Repository. It has been accepted for inclusion in Industrial and Manufacturing Systems Engineering Publications by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Optimal Resource Allocation Model to Prevent, Prepare, and Respond to Multiple Disruptions, with Application to the Deepwater Horizon Oil Spill and Hurricane Katrina Abstract Determining how to allocate resources in order to prevent and prepare for disruptions is a challenging task for homeland security officials. Disruptions ear uncertain events with uncertain consequences. Resources that could be used to prepare for unlikely disruptions may be better used for other priorities. This chapter presents an optimization model to help homeland security officials determine howo t allocate resources to prevent and prepare for multiple disruptions and how to allocate resources to respond to and recover from a disruption. In the resource allocation model, prevention reduces the probability of a disruption, and preparation and response both reduce the consequences of a disruption. The model is applied to the US Gulf Coast region and considers a Deepwater Horizon‐type oil spill and a hurricane similar to Hurricane Katrina. Keywords resource allocation, oil spill, hurricane mitigation, emergency response Disciplines Operational Research | Risk Analysis | Systems Engineering Comments This is a manuscript of a chapter published as MacKenzie, Cameron A., and Amro Al Kazimi. "Optimal Resource Allocation Model to Prevent, Prepare, and Respond to Multiple Disruptions, with Application to the Deepwater Horizon Oil Spill and Hurricane Katrina." In S. Chatterjee, R.T. Brigantic, and A.M. Waterworth, eds., Applied Risk Analysis for Guiding Homeland Security Policy. New York: John Wiley & Sons (2021): 381-403. DOI: 10.1002/9781119287490.ch15. Posted with permission. This book chapter is available at Iowa State University Digital Repository: https://lib.dr.iastate.edu/imse_pubs/261 Optimal Resource Allocation Model to Prevent, Prepare, and Respond to Multiple Disruptions, with Application to the Deepwater Horizon Oil Spill and Hurricane Katrina Cameron A. MacKenzie and Amro Al-Kazimi Industrial and Manufacturing Systems Engineering Department, Iowa State University Abstract: Determining how to allocate resources in order to prevent and prepare for disruptions is a challenging task for homeland security officials. Disruptions are uncertain events with uncertain consequences. Resources that could be used to prepare for unlikely disruptions may be better used for other priorities. This chapter presents an optimization model to help homeland security officials determine how to allocate resources to prevent and prepare for multiple disruptions and how to allocate resources to respond to and recover from a disruption. In the resource allocation model, prevention reduces the probability of a disruption, and preparation and response both reduce the consequences of a disruption. The model is applied to the U.S. Gulf Coast region and considers a Deepwater Horizon-type oil spill and a hurricane similar to Hurricane Katrina. Keywords: resource allocation, oil spill, hurricane, mitigation, emergency response 1.1 Introduction Disruptions, including man-induced accidents, terrorist attacks, and natural disasters, are becoming more costly and occurring more frequently. Globally, the cost of natural disasters has risen from about $50 billion per year in the 1980s to an annual average of $200 billion in the 2010s (Associated Press, 2014). From 2011 to 2013, the U.S. federal government spent approximately $136 billion in disaster relief (Weiss and Weidman, 2013). The Gulf of Mexico has been especially vulnerable to significant disruptions, such Hurricanes Katrina and Rita in 2005 and the Deepwater Horizon oil spill in 2010, which resulted in several fatalities, physical destruction, environmental damage, and business losses ranging from $40 billion to more than $100 billion. Al Kazimi and Mackenzie (2016) review the literature on the economic consequences of disruptions. The largest disruptions—such as an earthquake with a magnitude of 8 or more, Hurricane Katrina, and the September 11 terrorist attacks—led to economic losses that exceeded $100 billion. The Great Hanshin Earthquake in Japan in 1995 may have induced $144 billion in losses (Okuyama, 2009), and the 2011 Japanese earthquake and tsunami resulted in $84 billion in production losses in March and April (MacKenzie et al., 2012c). The United States suffered about $3 billion in lost wages due to Hurricane Sandy in 2012 (Park et al., 2014c), and the 2011 Joplin Tornado in Missouri was estimated to cost $6 billion (Richardson et al., 2014). Some potential but yet unrealized terrorist attacks, such as a dirty bomb or a shoulder-borne missile fired against an airplane, could lead to widespread panic, leading to losses in the tens or even hundreds of billions of dollars (Gordon et al., 2007, Park et al., 2014b). Disruptions that disable key infrastructure systems such as waterway ports (Rose and Wei, 2013, MacKenzie et al., 2012a) or the electric grid (Anderson et al., 2007) can induce economic losses of approximately $10 billion. The occurrence of these disruptions raises questions about how much should the United States prepare to mitigate these disruptions. The U.S. federal government spent almost 16 times more on disaster relief than disaster preparedness from 1985 to 2004 (Healy and Malhotra, 2009), but determining how best to spend money on disaster preparedness is challenging. Disruptions are uncertain, and knowing the time and geographical location of these disruptive events is impossible. There are many competing priorities for resources, and money spent preparing for disruptions cannot be spent on other important items, whether the money is from a federal, state, or local government’s budget or from the private sector. 1 Studies on resources used to prepare for disruptions generally conclude that the benefits of preparing for natural disasters exceed the costs (Rose et al., 2007, Garrett and Sobel, 2003, Healy and Malhotra, 2009). For example, levee improvements in New Orleans would have cost about $3-6 billion and saved New Orleans from the $120 billion in losses due to Hurricane Katrina (Godschalk et al., 2009). This chapter extends backward-looking benefit-cost analysis undertaken by these studies into a forward-looking model to help a decision maker determine how much to spend in preparing for a disruption while accounting for uncertainty in the disruption and competing priorities for other resources. Numerous operations research models recommend how resources should be allocated to prepare and respond to disruptive events (McLay, 2015, Altay and Green III, 2006, Banerjee and Gillespie, 1994). Disaster management models recommend the best way to allocate discrete resources (Chelst and Barlach, 1981, McLay and Mayorga, 2013), determine which vulnerable locations to protect (Church et al., 2004, Morton, 2011, Smith et al., 2013, Willis, 2007, Alderson et al., 2013), and schedule and organize emergency logistics (Campbell et al., 2008, Caunhye et al., 2012). Other models focus on protecting against specific disruptions such as earthquakes (Dodo et al., 2007, Dodo et al., 2005, Ermoliev et al., 2000, Gearhart et al., 2014) or hurricanes (Legg et al., 2013). Game theoretic models recommend allocations to protect against strategic actors such as terrorists (Bakir, 2011, Bier, 2007, Hausken, 2008, Major, 2002). Some game theoretic model trade off between preparing for terrorist attacks and preparing for natural disasters (Zhuang and Bier, 2007, Shan and Zhuang, 2013) and studying organizational cooperation for disaster relief (Coles and Zhuang, 2011). This chapter makes several unique contributions to the literature on operations research models for homeland security. First, it develops a general model of allocating resources that can be applied to any type of disruption. Second, the model accounts for uncertainty in the disruption and incorporates alternatives for what else could be done with resources if they are not used for disruptions. Third, the model is applied to two disruptions: an oil spill in the Gulf of Mexico and a hurricane in one of the five U.S. Gulf States. Unfortunately, the Gulf States experienced both of these disruptive events in the early 2000s. The likelihood of the hurricane is large enough that a decision maker should allocate a significant portion of the budget to preparing for a hurricane like Katrina. However, the chance of a large
Load more

Recommended publications
  • Human Vulnerability to Tornadoes in the United States Is Highest In
    1 Human vulnerability to tornadoes in the United States is highest in 2 urbanized areas of the Mid South ∗ 3 James B. Elsner and Tyler Fricker 4 Florida State University, Tallahassee, Florida ∗ 5 Corresponding author address: James B. Elsner, Department of Geography, Florida State Univer- 6 sity, 113 Collegiate Loop, Tallahassee, FL 32301. 7 E-mail: [email protected] Generated using v4.3.2 of the AMS LATEX template 1 ABSTRACT 8 Risk factors for tornado casualties are well known. Less understood is how 9 and to what degree these factors, after controlling for strength and the number 10 of people affected, vary over space and time. Here we fit models to casualty 11 counts from all casualty-producing tornadoes during the period 1995–2016 in 12 order to quantify the interactions between population and energy on casualty 13 (deaths plus injuries) rates. Results show that the more populated areas of the 14 Mid South are substantially and significantly more vulnerable to casualties 15 than elsewhere in the country. In this region casualty rates are significantly 16 higher on the weekend. Night and day casualty rates are similar regardless 17 of where the tornadoes occur. States with a high percentage of older people 18 (65+) tend to have greater vulnerability perhaps related to less agility and 19 fewer communication options. 2 20 1. Introduction 21 Nearly one fifth of all natural-hazards fatalities in the United States are the direct result of tor- 22 nadoes (National Oceanic and Atmospheric Administration 2015). A tornado that hits a city is 23 capable of inflicting hundreds or thousands of casualties.
    [Show full text]
  • 3.2 an Evaluation of Tornado Intensity Using Velocity and Strength Attributes from the Wsr-88D Mesocyclone Detection Algorithm
    3.2 AN EVALUATION OF TORNADO INTENSITY USING VELOCITY AND STRENGTH ATTRIBUTES FROM THE WSR-88D MESOCYCLONE DETECTION ALGORITHM Darrel M. Kingfield*,1,2, James G. LaDue3, and Kiel L. Ortega1,2 1Cooperative Institute for Mesoscale Meteorological Studies (CIMMS), Norman, OK 2NOAA/OAR/National Severe Storms Laboratory (NSSL), Norman, OK 3NOAA/NWS/OCWWS/Warning Decision Training Branch (WDTB), Norman, OK 1. INTRODUCTION undergone several improvements since these studies, including the integration of super-resolution data. National Weather Service (NWS) service Super-resolution data (Torres and Curtis, 2007) at the assessments following the 2011 April 27 southeast split-cut elevations reduces the effective beamwidth to US tornado outbreak, and the 2011 May 22 Joplin 1.02 from the legacy 1.38 , allowing for vortex tornado found that the population failed to personalize signatures⁰ to be resolved at longer⁰ ranges from the the potential severity of the tornadoes for which they radar (Brown et al. 2002; Brown et al. 2005). In this were warned. The lack of specific information paper, we investigate how the MDA output correlates contained within the warnings has been cited as a to maximum intensity found in a tornado path. major reason why more action was not taken (NOAA, 2011a, 2011b). As a result, a number of meetings 2. DATA & METHODS amongst government, the private and the academic sectors have begun to formulate a plan to improve 2.1 Acquisition & Playback impact-based warning services. In fact, this is the number one goal of the Weather Ready Nation The initial tornado track dataset was composed initiative within the NWS (NOAA, 2012).
    [Show full text]
  • Observations and Laboratory Simulations of Tornadoes in Complex Topographical Regions Christopher D
    Iowa State University Capstones, Theses and Graduate Theses and Dissertations Dissertations 2012 Observations and Laboratory Simulations of Tornadoes in Complex Topographical Regions Christopher D. Karstens Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/etd Part of the Atmospheric Sciences Commons, and the Meteorology Commons Recommended Citation Karstens, Christopher D., "Observations and Laboratory Simulations of Tornadoes in Complex Topographical Regions" (2012). Graduate Theses and Dissertations. 12778. https://lib.dr.iastate.edu/etd/12778 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Observations and laboratory simulations of tornadoes in complex topographical regions by Christopher Daniel Karstens A dissertation submitted to the graduate faculty in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY Major: Meteorology Program of Study Committee: William A. Gallus, Jr., Major Professor Partha P. Sarkar Bruce D. Lee Catherine A. Finley Raymond W. Arritt Xiaoqing Wu Iowa State University Ames, Iowa 2012 Copyright © Christopher Daniel Karstens, 2012. All rights reserved. ii TABLE OF CONTENTS LIST OF FIGURES ..............................................................................................
    [Show full text]
  • The Geneva Reports
    The Geneva Reports Risk and Insurance Research www.genevaassociation.org Extreme events and insurance: 2011 annus horribilis edited by Christophe Courbage and Walter R. Stahel No. 5 Marc h 2012 The Geneva Association (The International Association for the Study of Insurance Economics The Geneva Association is the leading international insurance think tank for strategically important insurance and risk management issues. The Geneva Association identifies fundamental trends and strategic issues where insurance plays a substantial role or which influence the insurance sector. Through the development of research programmes, regular publications and the organisation of international meetings, The Geneva Association serves as a catalyst for progress in the understanding of risk and insurance matters and acts as an information creator and disseminator. It is the leading voice of the largest insurance groups worldwide in the dialogue with international institutions. In parallel, it advances—in economic and cultural terms—the development and application of risk management and the understanding of uncertainty in the modern economy. The Geneva Association membership comprises a statutory maximum of 90 Chief Executive Officers (CEOs) from the world’s top insurance and reinsurance companies. It organises international expert networks and manages discussion platforms for senior insurance executives and specialists as well as policy-makers, regulators and multilateral organisations. The Geneva Association’s annual General Assembly is the most prestigious gathering of leading insurance CEOs worldwide. Established in 1973, The Geneva Association, officially the “International Association for the Study of Insurance Economics”, is based in Geneva, Switzerland and is a non-profit organisation funded by its members. Chairman: Dr Nikolaus von Bomhard, Chairman of the Board of Management, Munich Re, Munich.
    [Show full text]
  • Browndegerena Udel 0
    COMPLEXITIES OF MASS FATALITY INCIDENTS IN THE UNITED STATES: EXPLORING TELECOMMUNICATION FAILURE by Melissa L. Brown de Gerena A dissertation submitted to the Faculty of the University of Delaware in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Disaster Science and Management Winter 2021 © 2021 Melissa L. Brown de Gerena All Rights Reserved COMPLEXITIES OF MASS FATALITY INCIDENTS IN THE UNITED STATES: EXPLORING TELECOMMUNICATION FAILURE by Melissa L. Brown de Gerena Approved: __________________________________________________________ James Kendra, Ph.D. Director of the Disaster Science and Management Program Approved: __________________________________________________________ Maria P. Aristigueta, D.P.A. Dean of the Joseph R. Biden, Jr. School of Public Policy and Administration Approved: __________________________________________________________ Louis F. Rossi, Ph.D. Vice Provost for Graduate and Professional Education and Dean of the Graduate College I certify that I have read this dissertation and that in my opinion it meets the academic and professional standard required by the University as a dissertation for the degree of Doctor of Philosophy. Signed: __________________________________________________________ Sue McNeil, Ph.D. Professor in charge of dissertation I certify that I have read this dissertation and that in my opinion it meets the academic and professional standard required by the University as a dissertation for the degree of Doctor of Philosophy. Signed: __________________________________________________________ Melissa Melby, Ph.D. Member of dissertation committee I certify that I have read this dissertation and that in my opinion it meets the academic and professional standard required by the University as a dissertation for the degree of Doctor of Philosophy. Signed: __________________________________________________________ Rachel Davidson, Ph.D.
    [Show full text]
  • 6.3 a Comparison of High Resolution Tornado Surveys to Doppler Radar Observed Vortex Parameters: 2011-2012 Case Studies
    6.3 A COMPARISON OF HIGH RESOLUTION TORNADO SURVEYS TO DOPPLER RADAR OBSERVED VORTEX PARAMETERS: 2011-2012 CASE STUDIES James G. LaDue1*, Kiel Ortega2,3, Brandon Smith2,3, Greg Stumpf2,3, and Darrel Kingfield2,3 1NOAA/NWS/OCWWS/Warning Decision Training Branch (WDTB), Norman, OK 2NOAA/OAR/National Severe Storms Laboratory (NSSL), Norman, OK 3Cooperative Institute for Mesoscale Meteorological Studies (CIMMS), Norman, OK 1. INTRODUCTION significant portion of it. However, an impact-based tornado warning requires a real-time nowcast of tornado We are motivated to the goal of mitigating negative intensity. This study builds upon the work of Kingfield et outcomes from specific hazards like tornadoes as a al. (2012) and attempts to answer whether a radar- result of findings from recent NWS service based real-time nowcast is possible. Then contingent assessments. These findings revealed that warning on a positive answer, guidance can be developed based responses were often inadequate, sometimes due to on a more thorough study. lack of specific information regarding the magnitude of the threat and expected impacts (NOAA, 2011a & b). 2. BACKGROUND As a response, the Central Region of the NWS initiated an impact-based tornado warning experiment in 2012 2.1 Radar (Hudson et al. 2012b). Forecasters were expected to disseminate tiered tornado warnings based on the The major challenge to making a successful potential damage they may cause. Though nowcasting relationship between observed and radar-based tornado tornado intensity wasn’t explicitly included in the intensity is beam center offset relative to a vortex directives for the experiment, forecasters still based center.
    [Show full text]
  • Can Elevation Be Associated with the 2011 Joplin, Missouri, Tornado
    aphy & N r at Stimers and Paul, J Geogr Nat Disast 2017, 7:2 og u e ra l G f D DOI: 10.4172/2167-0587.1000202 o i s l a Journal of a s n t r e u r s o J ISSN: 2167-0587 Geography & Natural Disasters ResearchReview Article Article Open Access Can Elevation be Associated with the 2011 Joplin, Missouri, Tornado Fatalities? An Empirical Study Mitchel Stimers* and Bimal Kanti Paul Department of Natural and Physical Sciences, Cloud County Community College, Junction City, Kansas, 66441, USA Abstract The 2011 Joplin, MO, USA, tornado set a record in terms of the number of lives lost-no other tornado in the United States had killed as many as 161 people since 1950. There are many stochastic parameters that can affect the speed, direction, and magnitude of a tornado and it is thought that elevation may play a role in tornado intensity. The Joplin tornado created a track whose elevation was approximately 50 m from beginning to end, providing the impetus to examine whether or not the elevation change over the damage path tornado is associated with fatalities that resulted from the event. Using data collected from various sources, and the application of GIS as well as non-parametric statistics, we reveal that the elevation and tornado fatalities are inversely related, however; the relationship is not statistically significant, the reasons for which are discussed. Keywords: Joplin tornado; Tornado fatalities; Elevation; Damage Dating to 1950, when official tabulation began, no other tornado zone; GIS in the US had killed as many people as the Joplin event.
    [Show full text]
  • Joplin, Missouri
    Taking Action: Rebuilding Joplin after the Tornado Using the ATSDR Brownfields / Land Revitalization Action Model Green Complete Streets in the 20th Street Corridor Joplin, MO / January, 2014 Taking Action: Rebuilding Joplin after the Tornado 1 Using the ATSDR Brownfields / Land Revitalization Action Model Contents Land Revitalization Action Model ............................................................................4 1. Access to Nature ........................................................................................................................................5 2. Get Outside/ Be More Active ............................................................................................9 3. Clean Environment/ Accessibility ....................................................................... 13 4. Healthier/ More Affordable Food Choices ........................................ 19 5. Want to Feel Safer ............................................................................................................................... 21 6. Get Around Without a Car ................................................................................................. 22 7. Other Health Issues ......................................................................................................................... 23 8. Communications ................................................................................................................................. 24 9. Employment / Education ......................................................................................................
    [Show full text]
  • NWS Central Region Service Assessment Joplin, Missouri, Tornado – May 22, 2011
    NWS Central Region Service Assessment Joplin, Missouri, Tornado – May 22, 2011 U.S. DEPARTMENT OF COMMERCE National Oceanic and Atmospheric Administration National Weather Service, Central Region Headquarters Kansas City, MO July 2011 Cover Photographs Left: NOAA Radar image of Joplin Tornado. Right: Aftermath of Joplin, MO, tornado courtesy of Jennifer Spinney, Research Associate, University of Oklahoma, Social Science Woven into Meteorology. Preface On May 22, 2011, one of the deadliest tornadoes in United States history struck Joplin, Missouri, directly killing 159 people and injuring over 1,000. The tornado, rated EF-5 on the Enhanced Fujita Scale, with maximum winds over 200 mph, affected a significant part of a city with a population of more than 50,000 and a population density near 1,500 people per square mile. As a result, the Joplin tornado was the first single tornado in the United States to result in over 100 fatalities since the Flint, Michigan, tornado of June 8, 1953. Because of the rarity and historical significance of this event, a regional Service Assessment team was formed to examine warning and forecast services provided by the National Weather Service. Furthermore, because of the large number of fatalities that resulted from a warned tornado event, this Service Assessment will provide additional focus on dissemination, preparedness, and warning response within the community as they relate to NWS services. Service Assessments provide a valuable contribution to ongoing efforts by the National Weather Service to improve the quality, timeliness, and value of our products and services. Findings and recommendations from this assessment will improve techniques, products, services, and information provided to our partners and the American public.
    [Show full text]
  • Rapid Intensification, Storm Merging, and the 2011 Joplin Tornado The
    Rapid Intensification, Storm Merging, and the 2011 Joplin Tornado The rapid intensification of low-level vertical wind shear leading to tornado formation (tornadogenesis) may have a source in the interaction of cells merging with a parent storm. Our research uses high-resolution (sub-1 km) Weather Research and Forecasting Model (WRF) simulations to analyze the significance of storm mergers in the subsequent intensification of the parent circulation (mesocyclone) and tornadic vortex in the devastating 22 May 2011 Joplin, Missouri case. This event was noted for the rapid evolution of the storm, in association with storm mergers, from tornadogenesis to its peak EF-5 intensity in approximately four minutes according to the National Weather Service’s Event Assessment. By identifying the connection between the merger(s) and rapid intensification, a better understanding of tornadogenesis can be achieved. Approaching this event from a modeling perspective, we used real-data WRF simulations to reproduce the observed behavior in a controlled environment. Current simulations have replicated many aspects of storm structure and evolution observed on this day. The simulation results in tornadic-strength surface rotation shortly after the occurrence of a storm merger. Increased precipitation loading from the merging cell precedes a descending reflectivity core (DRC), which recent studies have found may play a role in the intensification of low-level rotation through increased convergence along the rear-flank gust front. The exact process leading to intensification will be the topic of forthcoming research. One opportunity afforded by modeling is the ability to test hypotheses by altering the environment or physical processes. Identifying if the storm would have been as intense without the presence of cell mergers is essential to quantifying the effect of these mergers.
    [Show full text]
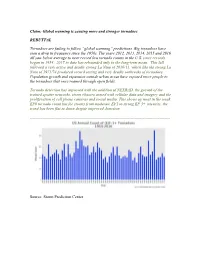
  • Claim: Global Warming Is Causing More and Stronger Tornadoes
    Claim: Global warming is causing more and stronger tornadoes REBUTTAL Tornadoes are failing to follow “global warming” predictions. Big tornadoes have seen a drop in frequency since the 1950s. The years 2012, 2013, 2014, 2015 and 2016 all saw below average to near record low tornado counts in the U.S. since records began in 1954. 2017 to date has rebounded only to the long-term mean. This lull followed a very active and deadly strong La Nina of 2010/11, which like the strong La Nina of 1973/74 produced record setting and very deadly outbreaks of tornadoes. Population growth and expansion outside urban areas have exposed more people to the tornadoes that once roamed through open fields. Tornado detection has improved with the addition of NEXRAD, the growth of the trained spotter networks, storm chasers armed with cellular data and imagery and the proliferation of cell phone cameras and social media. This shows up most in the weak EF0 tornado count but for storms from moderate EF1 to strong EF 3+ intensity, the trend has been flat to down despite improved detection. ------------------------------------------------------------------------------------------------------- Source: Storm Prediction Center Source: Storm Prediction Center Source: Storm Prediction Center Source: Storm Prediction Center Tornado outbreaks of significance occur most frequently in La Nina years, which are favored when the Pacific is cold as it was in the 1950s to the early 1970s and more recently 1999, 2008, 2010 and 2011. Source: Storm Prediction Center The death toll in the strong La Nina of 2011 was the highest since the “Superoutbreak” in the strong La Nina year of 1974.
    [Show full text]
  • The Dialogue: Volume 10, Issue 4
    A Quarterly Technical Assistance Journal on Disaster Behavioral Health Produced by the SAMHSA Disaster Technical Assistance Center IN THIS ISSUE 2 A Firefighter Peer Counselor’s Three Questions 5 Resilience in Joplin (and the Healing Power of Butterflies) 7 Strength After: The Importance 2014 | VOLUME 10 | ISSUE 4 of Disaster Behavioral Health Responders Staying Engaged Throughout Long-Term Recovery 10 Recommended Resources 11 Upcoming Events A statue dedicated to the firefighters who lost their lives in New York City on September 11, 2001. Photo: Patsy Lynch/FEMA IN THIS ISSUE 2 A Firefighter Peer Counselor’s 7 Strength After: The Importance Three Questions of Disaster Behavioral Health Responders Staying Engaged 5 Resilience in Joplin (and the Throughout Long-Term Recovery Healing Power of Butterflies) 10 Recommended Resources 11 Upcoming Events The Dialogue is a quarterly technical assistance journal on disaster behavioral health which is produced by the Substance Abuse and Mental Health Services Administration (SAMHSA) Disaster Technical Assistance Center (DTAC). Through the pages of The Dialogue, disaster behavioral health professionals share information and resources while examining the disaster behavioral health preparedness and response issues that are important to the field. The Dialogue also provides a comprehensive look at the disaster training and technical assistance services SAMHSA DTAC provides to prepare states, territories, tribes, and local entities so they can deliver effective behavioral health (mental health and substance abuse) responses to disasters. To receive The Dialogue, please go to SAMHSA’s homepage (http://www.samhsa.gov), enter your e-mail address in the “Mailing List” box on the right, and mark the checkbox for “SAMHSA’s Disaster Technical Assistance newsletter, The Dialogue,” which is listed in the Newsletters section.
    [Show full text]