Repetitively Pulsed High-Current Accelerators with Transformer Charging of Forming Lines
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lecture 09 Closing Switches.Pdf
High-voltage Pulsed Power Engineering, Fall 2018 Closing Switches Fall, 2018 Kyoung-Jae Chung Department of Nuclear Engineering Seoul National University Switch fundamentals The importance of switches in pulsed power systems In high power pulse applications, switches capable of handling tera-watt power and having jitter time in the nanosecond range are frequently needed. The rise time, shape, and amplitude of the generator output pulse depend strongly on the properties of the switches. The basic principle of switching is simple: at a proper time, change the property of the switch medium from that of an insulator to that of a conductor or the reverse. To achieve this effectively and precisely, however, is rather a complex and difficult task. It involves not only the parameters of the switch and circuit but also many physical and chemical processes. 2/44 High-voltage Pulsed Power Engineering, Fall 2018 Switch fundamentals Design of a switch requires knowledge in many areas. The property of the medium employed between the switch electrodes is the most important factor that determines the performance of the switch. Classification Medium: gas switch, liquid switch, solid switch Triggering mechanism: self-breakdown or externally triggered switches Charging mode: Statically charged or pulse charged switches No. of conducting channels: single channel or multi-channel switches Discharge property: volume discharge or surface discharge switches 3/44 High-voltage Pulsed Power Engineering, Fall 2018 Characteristics of typical switches A. Trigger pulse: a fast pulse supplied externally to initiate the action of switching, the nature of which may be voltage, laser beam or charged particle beam. -

CHARGE-Series Instructions
CHARGE-SERIES operating instructions REV216 Use for models CHARGE1000, CHARGE5000, CHARGE10000 DANGER do not use this unit unless you fully understand high -voltage and its hazards. DANGER A SERIOUS DEADLY SHOCK HAZARD WILL EXIST WHEN USING WITH HIGH ENERGY CAPACITORS ABOVE 50 J You can calculate joules by squaring the charging voltage, then multiplying by one half the capacitance in microfarads and dividing by 1 million. If over 50 J use extreme caution as improper contact can electrocute OR cause serious burns. PLEASE READ THE FOLLOWING VERY CAREFULLY Capacitive energy storage over 1000 joules MUST use for the high-voltage charge feed wire from the unit to the capacitors being SEVERAL FEET of a thin insulated preferably Teflon wire of a gauge that will disintegrate as a fuse between 100-500 amps. This wire should be sleeved into some polyethylene tubing that is available in a hardware store. You may even want to use several telescopic layers as this sleeving to provide a positive voltage rating and good mechanical rigidity. Note on knob Figure 1: Front Panel Controls CHARGE-SERIES ● rev216 © 2014 Information Unlimited www.amazing1.com 1 All rights reserved Figure 2: Back Panel CHARGE-SERIES ● rev216 © 2014 Information Unlimited www.amazing1.com 2 All rights reserved APPLICATIONS Electronic circuit charges up high energy banks of electrolytic, photo flash or other types storage capacitors from 200 to 30,000 V (depending on charger model) . Recommended capacities are between 100 to 10,000 µF. This equates out to many thousands of joules! Note the kinetic energy of a 30-06 is 750 J. -

Capillary Discharge XUV Radiation Source M
Acta Polytechnica Vol. 49 No. 2–3/2009 Capillary Discharge XUV Radiation Source M. Nevrkla A device producing Z-pinching plasma as a source of XUV radiation is described. Here a ceramic capacitor bank pulse-charged up to 100 kV is discharged through a pre-ionized gas-filled ceramic tube 3.2 mm in diameter and 21 cm in length. The discharge current has ampli- tude of 20 kA and a rise-time of 65 ns. The apparatus will serve as experimental device for studying of capillary discharge plasma, for test- ing X-ray optics elements and for investigating the interaction of water-window radiation with biological samples. After optimization it will be able to produce 46.9 nm laser radiation with collision pumped Ne-like argon ions active medium. Keywords: Capillary discharge, Z-pinch, XUV, soft X-ray, Rogowski coil, pulsed power. 1 Introduction column by the Lorentz force FL of a magnetic field B of flowing current I – a Z-pinch. First, the current flows along the In the region of XUV (eXtended Ultra Violet) radiation, walls of the capillary. The flowing current creates a magnetic i.e. in the region of ~ (0.2–100) nm there are two significant field, which affects the charged particles of the plasma by sub-regions. The first is the water-window region (2.3–4.4) a radial force. This force compresses the particles like a nm. Radiation in this region is highly absorbed in carbon, but snowplow till the magnetic pressure is equilibrated by the not much absorbed in water, so it is useful for observing or- plasma pressure. -

Type Here the Title of Your Paper
CIGRE-183 2019 CIGRE Canada Conference Montréal, Québec, September 16-19, 2019 The Research on the Key Equipment for 750kV Fixed Series Compensation in 3000m a.s.l. CHEN Yuanjun,ZHOU Qiwen,WANG Dechang,Gao Jian,Chen Wei, Zhang Daoxiong (1. NR Electric Co., Ltd., Nanjing 211102, China) SUMMARY The Qinghai 750kV fixed series compensation is officially put into operation in December 2018, it is located in the Qaidam area of China where the altitude is 3000m.In this paper, the high-altitude insulation calculation of the main equipment is carried out, and the power frequency withstand voltage, lightning impulse voltage, dry arc distance and creepage distance of each main equipment are proposed. Based on the project, we researched the key equipment such as spark gap and measurement system. According to the ANSYS simulation, the structure of the main electrode of the spark gap is optimized from ball-ball electrode to ball-plate electrode to make the self-trigger voltage be more stable. Considering the self-trigger voltage of the trigatron is up to 60kVpeak, the electrode structure of the trigatron is optimized to the structure with large curvature spherical design. The new trigatron has a better linearity and the maximum standard deviation is less than 0.6. In order to research the triggering characteristics, we completed the self-trigger test in the laboratory where the altitude is 0m, and fit the curve of the main gap air distance and the self-trigger voltage. Considering the altitude correction, we calculate the theoretical value of the main gap air distance according the self-trigger curve. -
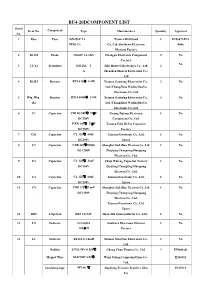
BU4-20DCOMPONENT LIST Serial Item No
BU4-20DCOMPONENT LIST Serial Item No. Component Type Manufacturer Quantity Approval No. 1 Fuse Fuse 20N250V 2A Xiamen Hollyland 1 E156471/E23 NF02-2A Co.,Ltd./Southern Electronic 4086 Element Factory 2 D1-D5 Diode 1N4007 1A,1KV Changda Electronic Component 5 No Factory No 3 T1-T2 Transistor D4128L 5 Jilin Huawei Electronics Co., Ltd. 2 A Shenzhen Shen’ai Electronics Co., Ltd 4 R3,R5 Resistor RT14 15Ω 1/4W Xiamen Gaoming Electronics Co., 2 No Ltd./ChangZhou WuJin HuaYu Electronic Co.,Ltd 5 R0、R1、 Resistor RT14 680kΩ 1/4W Xiamen Gaoming Electronics Co., 3 No R2 Ltd./ChangZhou WuJin HuaYu Electronic Co.,Ltd 6 C1 Capacitor CD11G 105℃ 22µF Yiyang Zijiang Electronic 1 No DC250V Component Co., Ltd. HXB 105℃ 22µF Xiamen Fala HeXin Capacitor DC250V Factory 7 C01 Capacitor CL 125℃ 68nF Xiamen Faratronic Co., Ltd. 1 No DC250V Epcos 8 C2 Capacitor CBB 125℃500pF Shanghai JiaLiBao Electron Co.,Ltd 1 No DC1250V Zhejiang Changxing Huaqiang Electron Co., Ltd. 9 C3 Capacitor CL 125℃ 22nF Zhuji Wufeng Capacitor Factory 1 No DC160V Zhejiang Changxing Huaqiang Electron Co., Ltd. 10 C4 Capacitor CL 125℃ 68nF Xiamen Faratronic Co., Ltd. 1 No DC250V Epcos 11 C5 Capacitor CBB 125℃5.6nF Shanghai JiaLiBao Electron Co.,Ltd 1 No DC1250V Zhejiang Changxing Huaqiang Electron Co., Ltd. Xiamen Faratronic Co., Ltd. Epcos 12 DB3 Trigatron DB3 Vz=32V Jinan Jifu Semiconductor Co., Ltd. 1 No 13 L0 Inductor LGA0410 Southern Electronic Element 1 No 100μH Factory 14 L1 Inductor EE161.5-1.6mH Xiamen XiaoTian Electronics Co., 1 No Ltd. -

14F1417 Doc 01
This document is made available through the declassification efforts and research of John Greenewald, Jr., creator of: The Black Vault The Black Vault is the largest online Freedom of Information Act (FOIA) document clearinghouse in the world. The research efforts here are responsible for the declassification of hundreds of thousands of pages released by the U.S. Government & Military. Discover the Truth at: http://www.theblackvault.com . - ·- - --·--·---------------------- A RAND NOTE ; '\Ill C: \ I I P;iS IIF ,\ ~l lrJ I T "•\ ~TI Cl l ·IIINI l\1':,\l'Cl :-o; J'R(\(;:c.N II . i•l. ''ii'll-l'•l\~ FR r: wsn:r: 'i\~ TT CJIJ·::: cl' l PrPpared For J)v2S4 forr.~ dat..:d 10/23/80 for t:o•ttrac t tiDI\903-; 8-C-018~ .and C l os~ified by multic.:..P=.lc::..' ...:s:..::o:..::u:..::r:..::c:..::I!:.:.S:...·----- Downgrade to o •._ ____ _ Declassify on____ _________ or Re·,iew on.--J\wiJ..;.'!.!ill:~:t~-·"'-!.... _ •...!. '1 !..!11____ _ .. ,.,. , : ~·~ . ' Un1:ut.ho-:-iz;J1 u; 6:wo tl ou:~ •--~ · ·- A RAND NOTE INDICATIONS Of A SOVIET PARTI CLE-S~! WF.APON PROGRAM II. PULSED-POWER CLOSlh~ SWITCHES (U) Simon Ka esel 1\uguc;t 1981 / N-1738- ARPA The Defense Advanced Re sear ch Projects Agency >- 8 ~ 81.. 10 ~ b.;.. r ... ~ -,4-- .,_~ -· ~..-.-.... - ·- BEST AVAILABLE COPY .. I.: I'· .u.: ·ilit:a J 1he research described i n this report was spon~ored by t h• Defense Advanced Research P~·oject$ Agency cnder ARPA Order No. 3520, Contract No. M!lA90J-78-I~-0 189, Director' s Office. -

What Is Pulsed Power
SAND2007-2984P PULSED POWER AT SANDIA NATIONAL LABORATORIES LABORATORIES NATIONAL SANDIA PULSED POWER AT WHAT IS PULSED POWER . the first forty years In the early days, this technology was often called ‘pulse power’ instead of pulsed power. In a pulsed power machine, low-power electrical energy from a wall plug is stored in a bank of capacitors and leaves them as a compressed pulse of power. The duration of the pulse is increasingly shortened until it is only billionths of a second long. With each shortening of the pulse, the power increases. The final result is a very short pulse with enormous power, whose energy can be released in several ways. The original intent of this technology was to use the pulse to simulate the bursts of radiation from exploding nuclear weapons. Anne Van Arsdall Anne Van Pulsed Power Timeline (over) Anne Van Arsdall SAND2007-????? ACKNOWLEDGMENTS Jeff Quintenz initiated this history project while serving as director of the Pulsed Power Sciences Center. Keith Matzen, who took over the Center in 2005, continued funding and support for the project. The author is grateful to the following people for their assistance with this history: Staff in the Sandia History Project and Records Management Department, in particular Myra O’Canna, Rebecca Ullrich, and Laura Martinez. Also Ramona Abeyta, Shirley Aleman, Anna Nusbaum, Michael Ann Sullivan, and Peggy Warner. For her careful review of technical content and helpful suggestions: Mary Ann Sweeney. For their insightful reviews and comments: Everet Beckner, Don Cook, Mike Cuneo, Tom Martin, Al Narath, Ken Prestwich, Jeff Quintenz, Marshall Sluyter, Ian Smith, Pace VanDevender, and Gerry Yonas. -

Investigation of a High–Power, High–Pressure Spark Gap Switch with High Repetition Rate
Investigation of a High–Power, High–Pressure Spark Gap Switch with High Repetition Rate Den Naturwissenschaftlichen Fakultäten der Friedrich–Alexander–Universität Erlangen–Nürnberg zur Erlangung des Doktorgrades vorgelegt von Hasibur Rahaman aus Indien Als Dissertation genehmigt von den Naturwissenschaftlichen Fakultäten der Universität Erlangen–Nürnberg Tag der mündlichen Prüfung: 12. 07. 2007 Vorsitzender der Promotionskommission: Prof. Dr. E. Bänsch Erstberichterstatter: Prof. Dr. K. Frank Zweitberichterstatter: Prof. Dr. J. Jacoby I Zusammenfassung Im Rahmen dieser Arbeit wurden die Eigenschaften von Mikroplasmen als Schaltmedium in einem miniaturisierten Hochdruckfunkenschalter untersucht. Entsprechend dem universellen Zündspannungsgesetz von Paschen gibt es bei gasgefüllten Schaltsystemen prinzipiell zwei Möglichkeiten der Realisierung: Entweder bei niederigen Gasdrücken (p < 100 Pa, Elektrodenabständen d ~ einige mm und Schaltspannungen U < 30 kV) oder bei Gasdrücken von 10 5 Pa und höher bei theoretisch unbegrenzt hohen Schaltspannungen und Elektrodenabständen d << 1 mm. Das Thyratron, der Pseudofunkenschalter und das Ignitron sind Beispiele von Niederdruckschaltsystemen, die sog. Funkenstrecken (engl. Spark Gaps) gehören dagegen zu den Hochdruckschaltsystemen. Gasgefüllte Schalter werden grundsätzlich verwendet, wenn in einem Schaltkreis langsam gespeicherte Energie sehr schnell an eine Last überführt werden soll. Von der Physik unterscheiden sich beide Klassen dadurch, daß in Niederdruckschaltsystemen das Zeitverhalten des Plasmaaufbaus -
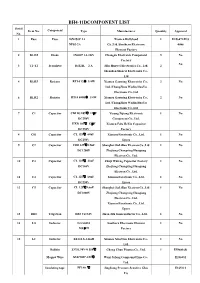
BH4-11DCOMPONENT LIST Serial Item No
BH4-11DCOMPONENT LIST Serial Item No. Component Type Manufacturer Quantity Approval No. 1 Fuse Fuse 20N250V 2A Xiamen Hollyland 1 E156471/E23 NF02-2A Co.,Ltd./Southern Electronic 4086 Element Factory 2 D1-D5 Diode 1N4007 1A,1KV Changda Electronic Component 5 No Factory No 3 T1-T2 Transistor D4124L 2 A Jilin Huawei Electronics Co., Ltd. 2 Shenzhen Shen’ai Electronics Co., Ltd 4 R3,R5 Resistor RT14 12Ω 1/4W Xiamen Gaoming Electronics Co., 2 No Ltd./ChangZhou WuJin HuaYu Electronic Co.,Ltd 6 R1,R2 Resistor RT14 680kΩ 1/4W Xiamen Gaoming Electronics Co., 2 No Ltd./ChangZhou WuJin HuaYu Electronic Co.,Ltd 7 C1 Capacitor CD11G 105℃ 12µF Yiyang Zijiang Electronic 1 No DC250V Component Co., Ltd. HXB 105℃ 12µF Xiamen Fala HeXin Capacitor DC250V Factory 8 C01 Capacitor CL 125℃ 68nF Xiamen Faratronic Co., Ltd. 1 No DC250V Epcos 9 C2 Capacitor CBB 125℃1.5nF Shanghai JiaLiBao Electron Co.,Ltd 1 No DC1200V Zhejiang Changxing Huaqiang Electron Co., Ltd. 10 C3 Capacitor CL 125℃ 22nF Zhuji Wufeng Capacitor Factory 1 No DC160V Zhejiang Changxing Huaqiang Electron Co., Ltd. 11 C4 Capacitor CL 125℃ 68nF Xiamen Faratronic Co., Ltd. 1 No DC250V Epcos 12 C5 Capacitor CL 125℃5.6nF Shanghai JiaLiBao Electron Co.,Ltd 1 No DC1000V Zhejiang Changxing Huaqiang Electron Co., Ltd. Xiamen Faratronic Co., Ltd. Epcos 13 DB3 Trigatron DB3 Vz=32V Jinan Jifu Semiconductor Co., Ltd. 1 No 14 L0 Inductor LGA0410 Southern Electronic Element 1 No 200μH Factory 15 L1 Inductor EE132.5-3.0mH Xiamen XiaoTian Electronics Co., 1 No Ltd. -

1999: Development of a Hermetically Sealed, High
See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/3837806 Development of a hermetically sealed, high energy trigatron switch for high repetition rate applications Conference Paper · February 1999 DOI: 10.1109/PPC.1999.825433 · Source: IEEE Xplore CITATIONS READS 8 107 6 authors, including: Jane Lehr W.D. Prather University of New Mexico Air Force Research Laboratory, Kirtland AFB, NM, United States 147 PUBLICATIONS 1,228 CITATIONS 106 PUBLICATIONS 1,108 CITATIONS SEE PROFILE SEE PROFILE Some of the authors of this publication are also working on these related projects: Cascade switches View project Quarter-wave Switched Oscillator View project All content following this page was uploaded by Jane Lehr on 15 February 2015. The user has requested enhancement of the downloaded file. DEVELOPMENT OF A HERMETICALLY SEALED, HIGH ENERGY TRIGATRON SWITCH FOR HIGH REPETETION RATE APPLICATIONS J.M. L&r*, M.D. Abdalla+, B. Cockrehan?, F. Gruner*, M.C. Skipper+ and W.D. Prather Air Force ResearchLaboratory, Directed Energy Directorate, Kirtland AFB, New Mexico Abstract pulsed power systems. Spark gaps can be relatively Triggeredgas switchesincrease the reliability of pulsed simpleyet exhibit excellentswitching performanceover a power systems. In particular, the performance of high wide pammeterspace. The principal advantagesof spark power, repetitively rated impulse generators is greatly gaps are their fast turn on time, good current handling enhancedby including a triggered switch In order to capability, wide operating voltage range, and acceptable simplify the pulsed power subsystemfor field testing, the pulse repetition rate. In general,high pulse repetition rate Air Force has developeda reliable, fully sealed,trigatron spark gap switchesrequire the insulating gas to be flowed switch. -

Electronics: Retrospective View, Successes and Prospects of Its Development
View metadata, citation and similar papers at core.ac.uk brought to you by CORE Electrical Engineering. Great Events. Famous Names UDC 621.3: 537.8: 910.4 doi: 10.20998/2074-272X.2018.1.01 M.I. Baranov AN ANTHOLOGY OF THE DISTINGUISHED ACHIEVEMENTS IN SCIENCE AND TECHNIQUE. PART 42: ELECTRONICS: RETROSPECTIVE VIEW, SUCCESSES AND PROSPECTS OF ITS DEVELOPMENT Purpose. Preparation of brief scientific and technical review about sources, retrospective view, basic stages, achievements, problems, trends and prospects of development of world electronics for period of 20th-21st centuries. Methodology. Known scientific methods of collection, analysis and analytical treatment of the opened scientific and technical information of world level in area of a vacuum electronics, semiconductor electronics, vacuum microelectronics and nanoelectronics, and also optical electronics. Results. A brief analytical scientific and technical review is resulted about the primary and present states, achievements, trends and prospects of development of electronics in the developed countries of the world. From positions of approach of the systems advantages and lacks of semiconductor microelectronics are described as compared to a vacuum electronics. Considerable progress is marked in development of semiconductor element base (microtransistors, microprocessors, microcontrollers and other) for creation of different electronic devices and computing engineering. Information, touching the determining deposit of electronic companies of the «Silicon Valley» in the USA in providing of technological breach in area of modern microelectronics, production of computers and their microprocessors, software and creation of devices of mobile communication development, is resulted. The basic problems of space microelectronics are affected. The possible ways of further development are indicated in the world of electronics, including vacuum microelectronics and nanoelectronics, and also optical electronics. -

Design of a Low-Cost Ultra-Wide-Band Radar Platform
sensors Article Design of a Low-Cost Ultra-Wide-Band Radar Platform Marko Malajner *,†, Danijel Šipoš † and Dušan Gleich † Faculty of Electrical Engineering and Computer Science, University of Maribor, Koroška Cesta 46, 2000 Maribor, Slovenia; [email protected] (D.Š.); [email protected] (D.G.) * Correspondence: [email protected] † These authors contributed equally to this work. Received: 24 March 2020; Accepted: 15 May 2020; Published: 18 May 2020 Abstract: This paper proposes an improved design of a pulse-based radar. An improved design of a pulse generator is presented using step recovery diodes and a signal mixer for the received signal. Two-step recovery diodes produce pulses of 120 ps in duration. A pulse generator is improved by removing the negative power supply, resulting in a reduced number of electronic pulses. A sampling mixer at the receiver’s site receives the generated signal and stretches it from picoseconds into microseconds. The improved pulse generator is also used in the sampling mixer as a strobe pulse generator, which makes the sampling mixer much simpler. The stretched signal is then sampled by a low sample rate using an analog to digital converter. The proposed radar design achieves up to 8 GHz bandwidth and an equivalent receiving sample rate of about 100 GSa/s. The radar is controlled using a software-defined radio called Red Pitaya, which is also used for data acquisition. The proposed radar design uses widely available commercial components, which makes radar design widely available with low cost implementation. Keywords: ultra-wide-band; pulse radar; ground penetrating radar; sampling mixer; pulse generator 1.