DOCSLIB.ORG

Abstract Algebra: Monoids, Groups, Rings

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Abstract Algebra: Monoids, Groups, Rings Notes on Abstract Algebra John Perry University of Southern Mississippi [email protected] http://www.math.usm.edu/perry/ Copyright 2009 John Perry www.math.usm.edu/perry/ Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States You are free: to Share—to copy, distribute and transmit the work • to Remix—to adapt the work Under• the following conditions: Attribution—You must attribute the work in the manner specified by the author or licen- • sor (but not in any way that suggests that they endorse you or your use of the work). Noncommercial—You may not use this work for commercial purposes. • Share Alike—If you alter, transform, or build upon this work, you may distribute the • resulting work only under the same or similar license to this one. With the understanding that: Waiver—Any of the above conditions can be waived if you get permission from the copy- • right holder. Other Rights—In no way are any of the following rights affected by the license: • Your fair dealing or fair use rights; ◦ Apart from the remix rights granted under this license, the author’s moral rights; ◦ Rights other persons may have either in the work itself or in how the work is used, ◦ such as publicity or privacy rights. Notice—For any reuse or distribution, you must make clear to others the license terms of • this work. The best way to do this is with a link to this web page: http://creativecommons.org/licenses/by-nc-sa/3.0/us/legalcode Table of Contents Reference sheet for notation...........................................................iv A few acknowledgements..............................................................vi Preface ...............................................................................vii Overview ...........................................................................vii Three interesting problems ............................................................1 Part . Monoids 1. From integers to monoids ...........................................................4 1. Some facts about the integers .........................................................5 2. Integers, monomials, and monoids ...................................................11 3. Direct Products and Isomorphism ....................................................16 Part I. Groups 2. Groups ............................................................................23 1. Groups ...........................................................................23 2. The symmetries of a triangle.........................................................31 3. Cyclic groups and order ............................................................37 4. The roots of unity ..................................................................44 5. Elliptic Curves ....................................................................46 3. Subgroups .........................................................................50 1. Subgroups.........................................................................50 2. Cosets ............................................................................54 3. Lagrange’s Theorem ................................................................59 4. Quotient Groups ..................................................................62 5. “Clockwork” groups................................................................67 6. “Solvable” groups ..................................................................71 4. Isomorphisms ......................................................................76 1. Homomorphisms ..................................................................76 2. Consequences of isomorphism .......................................................82 3. The Isomorphism Theorem ..........................................................87 4. Automorphisms and groups of automorphisms.........................................91 5. Groups of permutations............................................................96 1. Permutations......................................................................96 2. Groups of permutations ...........................................................105 3. Dihedral groups ..................................................................107 4. Cayley’s Theorem .................................................................112 i 5. Alternating groups ................................................................115 6. The 15-puzzle ....................................................................120 6. Number theory ...................................................................123 1. GCD and the Euclidean Algorithm .................................................123 2. The Chinese Remainder Theorem ...................................................127 3. Multiplicative clockwork groups ....................................................134 4. Euler’s Theorem ..................................................................140 5. RSA Encryption ..................................................................144 Part II. Rings 7. Rings .............................................................................151 1. A structure for addition and multiplication ..........................................151 2. Integral Domains and Fields .......................................................154 3. Polynomial rings .................................................................159 4. Euclidean domains................................................................167 8. Ideals .............................................................................173 1. Ideals............................................................................173 2. Principal Ideals ...................................................................179 3. Prime and maximal ideals .........................................................182 4. Quotient Rings ...................................................................185 5. Finite Fields I ....................................................................190 6. Ring isomorphisms ...............................................................196 7. A generalized Chinese Remainder Theorem ..........................................201 8. Nullstellensatz....................................................................204 9. Rings and polynomial factorization................................................207 1. The link between factoring and ideals ...............................................207 2. Unique Factorization domains .....................................................210 3. Finite fields II ....................................................................213 4. Polynomial factorization in finite fields ..............................................218 5. Factoring integer polynomials ......................................................223 10. Gröbner bases ...................................................................228 1. Gaussian elimination ............................................................229 2. Monomial orderings .............................................................235 3. Matrix representations of monomial orderings ......................................242 4. The structure of a Gröbner basis ...................................................245 5. Buchberger’s algorithm ...........................................................255 6. Elementary applications ..........................................................263 11. Advanced methods of computing Gröbner bases ..................................268 1. The Gebauer-Möller algorithm ....................................................268 ii 2. The F4 algorithm ................................................................277 3. Signature-based algorithms to compute a Gröbner basis...............................282 Part III. Appendices Where can I go from here? ...........................................................291 Advanced group theory .............................................................291 Advanced ring theory ..............................................................291 Applications.......................................................................291 Hints to Exercises ...................................................................292 Hints to Chapter1 .................................................................292 Hints to Chapter2 .................................................................293 Hints to Chapter3 .................................................................294 Hints to Chapter4 .................................................................295 Hints to Chapter5 .................................................................296 Hints to Chapter6 .................................................................296 Hints to Chapter7 .................................................................297 Hints to Chapter8 .................................................................298 Hints to Chapter9 .................................................................299 Hints to Chapter 10 ................................................................299 Index................................................................................300 References...........................................................................304 iii Reference sheet for notation [r ] the element r + nZ of Zn g the group (or ideal) generated by g h i A3 the alternating group on three elements A/ G for G a group, A is a normal subgroup of G A/ R for R a ring, A is an ideal of R C
Load more

Recommended publications
  • 7. Euclidean Domains Let R Be an Integral Domain. We Want to Find Natural Conditions on R Such That R Is a PID. Looking at the C
    7. Euclidean Domains Let R be an integral domain. We want to find natural conditions on R such that R is a PID. Looking at the case of the integers, it is clear that the key property is the division algorithm. Definition 7.1. Let R be an integral domain. We say that R is Eu- clidean, if there is a function d: R − f0g −! N [ f0g; which satisfies, for every pair of non-zero elements a and b of R, (1) d(a) ≤ d(ab): (2) There are elements q and r of R such that b = aq + r; where either r = 0 or d(r) < d(a). Example 7.2. The ring Z is a Euclidean domain. The function d is the absolute value. Definition 7.3. Let R be a ring and let f 2 R[x] be a polynomial with coefficients in R. The degree of f is the largest n such that the coefficient of xn is non-zero. Lemma 7.4. Let R be an integral domain and let f and g be two elements of R[x]. Then the degree of fg is the sum of the degrees of f and g. In particular R[x] is an integral domain. Proof. Suppose that f has degree m and g has degree n. If a is the leading coefficient of f and b is the leading coefficient of g then f = axm + ::: and f = bxn + :::; where ::: indicate lower degree terms then fg = (ab)xm+n + :::: As R is an integral domain, ab 6= 0, so that the degree of fg is m + n.
    [Show full text]
  • Advanced Discrete Mathematics Mm-504 &
    1 ADVANCED DISCRETE MATHEMATICS M.A./M.Sc. Mathematics (Final) MM-504 & 505 (Option-P3) Directorate of Distance Education Maharshi Dayanand University ROHTAK – 124 001 2 Copyright © 2004, Maharshi Dayanand University, ROHTAK All Rights Reserved. No part of this publication may be reproduced or stored in a retrieval system or transmitted in any form or by any means; electronic, mechanical, photocopying, recording or otherwise, without the written permission of the copyright holder. Maharshi Dayanand University ROHTAK – 124 001 Developed & Produced by EXCEL BOOKS PVT. LTD., A-45 Naraina, Phase 1, New Delhi-110 028 3 Contents UNIT 1: Logic, Semigroups & Monoids and Lattices 5 Part A: Logic Part B: Semigroups & Monoids Part C: Lattices UNIT 2: Boolean Algebra 84 UNIT 3: Graph Theory 119 UNIT 4: Computability Theory 202 UNIT 5: Languages and Grammars 231 4 M.A./M.Sc. Mathematics (Final) ADVANCED DISCRETE MATHEMATICS MM- 504 & 505 (P3) Max. Marks : 100 Time : 3 Hours Note: Question paper will consist of three sections. Section I consisting of one question with ten parts covering whole of the syllabus of 2 marks each shall be compulsory. From Section II, 10 questions to be set selecting two questions from each unit. The candidate will be required to attempt any seven questions each of five marks. Section III, five questions to be set, one from each unit. The candidate will be required to attempt any three questions each of fifteen marks. Unit I Formal Logic: Statement, Symbolic representation, totologies, quantifiers, pradicates and validity, propositional logic. Semigroups and Monoids: Definitions and examples of semigroups and monoids (including those pertaining to concentration operations).
    [Show full text]
  • An Elementary Approach to Boolean Algebra
    Eastern Illinois University The Keep Plan B Papers Student Theses & Publications 6-1-1961 An Elementary Approach to Boolean Algebra Ruth Queary Follow this and additional works at: https://thekeep.eiu.edu/plan_b Recommended Citation Queary, Ruth, "An Elementary Approach to Boolean Algebra" (1961). Plan B Papers. 142. https://thekeep.eiu.edu/plan_b/142 This Dissertation/Thesis is brought to you for free and open access by the Student Theses & Publications at The Keep. It has been accepted for inclusion in Plan B Papers by an authorized administrator of The Keep. For more information, please contact [email protected]. r AN ELEr.:ENTARY APPRCACH TC BCCLF.AN ALGEBRA RUTH QUEAHY L _J AN ELE1~1ENTARY APPRCACH TC BC CLEAN ALGEBRA Submitted to the I<:athematics Department of EASTERN ILLINCIS UNIVERSITY as partial fulfillment for the degree of !•:ASTER CF SCIENCE IN EJUCATION. Date :---"'f~~-----/_,_ffo--..i.-/ _ RUTH QUEARY JUNE 1961 PURPOSE AND PLAN The purpose of this paper is to provide an elementary approach to Boolean algebra. It is designed to give an idea of what is meant by a Boclean algebra and to supply the necessary background material. The only prerequisite for this unit is one year of high school algebra and an open mind so that new concepts will be considered reason­ able even though they nay conflict with preconceived ideas. A mathematical science when put in final form consists of a set of undefined terms and unproved propositions called postulates, in terrrs of which all other concepts are defined, and from which all other propositions are proved.
    [Show full text]
  • Algebraic Number Theory
    Algebraic Number Theory William B. Hart Warwick Mathematics Institute Abstract. We give a short introduction to algebraic number theory. Algebraic number theory is the study of extension fields Q(α1; α2; : : : ; αn) of the rational numbers, known as algebraic number fields (sometimes number fields for short), in which each of the adjoined complex numbers αi is algebraic, i.e. the root of a polynomial with rational coefficients. Throughout this set of notes we use the notation Z[α1; α2; : : : ; αn] to denote the ring generated by the values αi. It is the smallest ring containing the integers Z and each of the αi. It can be described as the ring of all polynomial expressions in the αi with integer coefficients, i.e. the ring of all expressions built up from elements of Z and the complex numbers αi by finitely many applications of the arithmetic operations of addition and multiplication. The notation Q(α1; α2; : : : ; αn) denotes the field of all quotients of elements of Z[α1; α2; : : : ; αn] with nonzero denominator, i.e. the field of rational functions in the αi, with rational coefficients. It is the smallest field containing the rational numbers Q and all of the αi. It can be thought of as the field of all expressions built up from elements of Z and the numbers αi by finitely many applications of the arithmetic operations of addition, multiplication and division (excepting of course, divide by zero). 1 Algebraic numbers and integers A number α 2 C is called algebraic if it is the root of a monic polynomial n n−1 n−2 f(x) = x + an−1x + an−2x + ::: + a1x + a0 = 0 with rational coefficients ai.
    [Show full text]
  • Properties & Multiplying a Polynomial by a Monomial Date
    Algebra I Block Name Unit #1: Linear Equations & Inequalities Period Lesson #2: Properties & Multiplying a Polynomial by a Monomial Date Properties In algebra, it is important to know certain properties. These properties are basically rules that allow us to manipulate and work with equations in order to solve for a given variable. We will be dealing with them all year, and you’ve probably actually been using them for awhile without even realizing it! The Commutative Property deals with the order of things. In other words, if I switch the order of two or more items, will my answer be the same? The Commutative Property of Addition states that when it comes to adding two different numbers, the order does . The Commutative Property of Multiplication states that when it comes to multiplying two different numbers, the order does . When it comes to subtracting and dividing numbers, the order matter, so there are no commutative properties for subtraction or division. The Associative Property deals with how things are grouped together. In other words, if I regroup two or more numbers, will my answer still be the same? Just like the commutative property, the associative property applies to addition and multiplication only. There are Identity Properties that apply all four basic operations. When it comes to identity properties, just ask yourself “What can I do to keep the answer the same?” The identity property of addition states that if I add to anything, it will stay the same. The same is true for subtraction. The identity property of multiplication states that if I multiply anything by _______, it will stay the same.
    [Show full text]
  • Ring (Mathematics) 1 Ring (Mathematics)
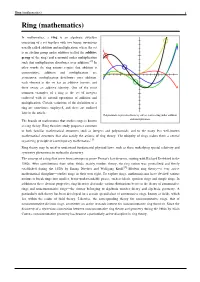
    Ring (mathematics) 1 Ring (mathematics) In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition (called the additive group of the ring) and a monoid under multiplication such that multiplication distributes over addition.a[›] In other words the ring axioms require that addition is commutative, addition and multiplication are associative, multiplication distributes over addition, each element in the set has an additive inverse, and there exists an additive identity. One of the most common examples of a ring is the set of integers endowed with its natural operations of addition and multiplication. Certain variations of the definition of a ring are sometimes employed, and these are outlined later in the article. Polynomials, represented here by curves, form a ring under addition The branch of mathematics that studies rings is known and multiplication. as ring theory. Ring theorists study properties common to both familiar mathematical structures such as integers and polynomials, and to the many less well-known mathematical structures that also satisfy the axioms of ring theory. The ubiquity of rings makes them a central organizing principle of contemporary mathematics.[1] Ring theory may be used to understand fundamental physical laws, such as those underlying special relativity and symmetry phenomena in molecular chemistry. The concept of a ring first arose from attempts to prove Fermat's last theorem, starting with Richard Dedekind in the 1880s. After contributions from other fields, mainly number theory, the ring notion was generalized and firmly established during the 1920s by Emmy Noether and Wolfgang Krull.[2] Modern ring theory—a very active mathematical discipline—studies rings in their own right.
    [Show full text]
  • Unit and Unitary Cayley Graphs for the Ring of Gaussian Integers Modulo N
    Quasigroups and Related Systems 25 (2017), 189 − 200 Unit and unitary Cayley graphs for the ring of Gaussian integers modulo n Ali Bahrami and Reza Jahani-Nezhad Abstract. Let [i] be the ring of Gaussian integers modulo n and G( [i]) and G be the Zn Zn Zn[i] unit graph and the unitary Cayley graph of Zn[i], respectively. In this paper, we study G(Zn[i]) and G . Among many results, it is shown that for each positive integer n, the graphs G( [i]) Zn[i] Zn and G are Hamiltonian. We also nd a necessary and sucient condition for the unit and Zn[i] unitary Cayley graphs of Zn[i] to be Eulerian. 1. Introduction Finding the relationship between the algebraic structure of rings using properties of graphs associated to them has become an interesting topic in the last years. There are many papers on assigning a graph to a ring, see [1], [3], [4], [5], [7], [6], [8], [10], [11], [12], [17], [19], and [20]. Let R be a commutative ring with non-zero identity. We denote by U(R), J(R) and Z(R) the group of units of R, the Jacobson radical of R and the set of zero divisors of R, respectively. The unitary Cayley graph of R, denoted by GR, is the graph whose vertex set is R, and in which fa; bg is an edge if and only if a − b 2 U(R). The unit graph G(R) of R is the simple graph whose vertices are elements of R and two distinct vertices a and b are adjacent if and only if a + b in U(R) .
    [Show full text]
  • Vector Spaces
    Chapter 1 Vector Spaces Linear algebra is the study of linear maps on finite-dimensional vec- tor spaces. Eventually we will learn what all these terms mean. In this chapter we will define vector spaces and discuss their elementary prop- erties. In some areas of mathematics, including linear algebra, better the- orems and more insight emerge if complex numbers are investigated along with real numbers. Thus we begin by introducing the complex numbers and their basic✽ properties. 1 2 Chapter 1. Vector Spaces Complex Numbers You should already be familiar with the basic properties of the set R of real numbers. Complex numbers were invented so that we can take square roots of negative numbers. The key idea is to assume we have i − i The symbol was√ first a square root of 1, denoted , and manipulate it using the usual rules used to denote −1 by of arithmetic. Formally, a complex number is an ordered pair (a, b), the Swiss where a, b ∈ R, but we will write this as a + bi. The set of all complex mathematician numbers is denoted by C: Leonhard Euler in 1777. C ={a + bi : a, b ∈ R}. If a ∈ R, we identify a + 0i with the real number a. Thus we can think of R as a subset of C. Addition and multiplication on C are defined by (a + bi) + (c + di) = (a + c) + (b + d)i, (a + bi)(c + di) = (ac − bd) + (ad + bc)i; here a, b, c, d ∈ R. Using multiplication as defined above, you should verify that i2 =−1.
    [Show full text]
  • NOTES on UNIQUE FACTORIZATION DOMAINS Alfonso Gracia-Saz, MAT 347
    Unique-factorization domains MAT 347 NOTES ON UNIQUE FACTORIZATION DOMAINS Alfonso Gracia-Saz, MAT 347 Note: These notes summarize the approach I will take to Chapter 8. You are welcome to read Chapter 8 in the book instead, which simply uses a different order, and goes in slightly different depth at different points. If you read the book, notice that I will skip any references to universal side divisors and Dedekind-Hasse norms. If you find any typos or mistakes, please let me know. These notes complement, but do not replace lectures. Last updated on January 21, 2016. Note 1. Through this paper, we will assume that all our rings are integral domains. R will always denote an integral domains, even if we don't say it each time. Motivation: We know that every integer number is the product of prime numbers in a unique way. Sort of. We just believed our kindergarden teacher when she told us, and we omitted the fact that it needed to be proven. We want to prove that this is true, that something similar is true in the ring of polynomials over a field. More generally, in which domains is this true? In which domains does this fail? 1 Unique-factorization domains In this section we want to define what it means that \every" element can be written as product of \primes" in a \unique" way (as we normally think of the integers), and we want to see some examples where this fails. It will take us a few definitions. Definition 2. Let a; b 2 R.
    [Show full text]
  • Euclidean Quadratic Forms and Adc-Forms: I
    EUCLIDEAN QUADRATIC FORMS AND ADC-FORMS: I PETE L. CLARK We denote by N the non-negative integers (including 0). Throughout R will denote a commutative, unital integral domain and K its fraction • field. We write R for R n f0g and ΣR for the set of height one primes of R. If M and N are monoids (written multiplicatively, with identity element 1), a monoid homomorphism f : M ! N is nondegenerate if f(x) = 1 () x = 1. Introduction The goal of this work is to set up the foundations and begin the systematic arith- metic study of certain classes of quadratic forms over a fairly general class of integral domains. Our work here is concentrated around that of two definitions, that of Eu- clidean form and ADC form. These definitions have a classical flavor, and various special cases of them can be found (most often implicitly) in the literature. Our work was particularly motivated by the similarities between two classical theorems. × Theorem 1. (Aubry, Davenport-Cassels) LetP A = (aij) be a symmetric n n Z matrix with coefficients in , and let q(x) = 1≤i;j≤n aijxixj be a positive definite integral quadratic form. Suppose that for all x 2 Qn, there exists y 2 Zn such that q(x − y) < 1. Then if d 2 Z is such that there exists x 2 Qn with q(x) = d, there exists y 2 Zn such that q(y) = d. 2 2 2 Consider q(x) = x1 + x2 + x3. It satisfies the hypotheses of the theorem: approxi- mating a vector x 2 Q3 by a vector y 2 Z3 of nearest integer entries, we get 3 (x − y )2 + (x − y )2 + (x − y )2 ≤ < 1: 1 1 2 2 3 3 4 Thus Theorem 1 shows that every integer which is the sum of three rational squares is also the sum of three integral squares.
    [Show full text]
  • Section IX.46. Euclidean Domains
    IX.46. Euclidean Domains 1 Section IX.46. Euclidean Domains Note. Fraleigh comments at the beginning of this section: “Now a modern tech- nique of mathematics is to take some clearly related situations and try to bring them under one roof by abstracting the important ideas common to them.” In this section, we take the idea of the division algorithm for integral domain Z and generalize it to other integral domains. Note. Recall: 1. Division Algorithm for Z (Theorem 6.3). If m is a positive integer and n is any integer, then there exist unique integers q and r such that n = mq + r and 0 ≤ r < m. 2. Division Algorithm for [x] (Theorem 23.1). n n−1 Let F be a field and let f(x)= anx + an−1x + ··· + a1x + a0 and g(x)= n m−1 bnx + bm−1x + ···+ b1x + b0 be two elements of F [x], with an and bm both nonzero elements of F and m > 0. Then there are unique polynomials q(x) and r(x) in F [x] such that f(x) = g(x)q(x)+ r(x), where either r(x)=0or the degree of r(x) is less than the degree m of g(x). Note. We now introduce a function which maps an integral domain into the nonnegative integers and use the values of this function to replace the ideas of “remainder” in Z and “degree” in F [x]. IX.46. Euclidean Domains 2 Definition 46.1. A Euclidean norm on an integral domain D is a function v mapping the nonzero elements of D into the nonnegative integers such that the following conditions are satisfied: 1.
    [Show full text]
  • RING THEORY 1. Ring Theory a Ring Is a Set a with Two Binary Operations
    CHAPTER IV RING THEORY 1. Ring Theory A ring is a set A with two binary operations satisfying the rules given below. Usually one binary operation is denoted `+' and called \addition," and the other is denoted by juxtaposition and is called \multiplication." The rules required of these operations are: 1) A is an abelian group under the operation + (identity denoted 0 and inverse of x denoted x); 2) A is a monoid under the operation of multiplication (i.e., multiplication is associative and there− is a two-sided identity usually denoted 1); 3) the distributive laws (x + y)z = xy + xz x(y + z)=xy + xz hold for all x, y,andz A. Sometimes one does∈ not require that a ring have a multiplicative identity. The word ring may also be used for a system satisfying just conditions (1) and (3) (i.e., where the associative law for multiplication may fail and for which there is no multiplicative identity.) Lie rings are examples of non-associative rings without identities. Almost all interesting associative rings do have identities. If 1 = 0, then the ring consists of one element 0; otherwise 1 = 0. In many theorems, it is necessary to specify that rings under consideration are not trivial, i.e. that 1 6= 0, but often that hypothesis will not be stated explicitly. 6 If the multiplicative operation is commutative, we call the ring commutative. Commutative Algebra is the study of commutative rings and related structures. It is closely related to algebraic number theory and algebraic geometry. If A is a ring, an element x A is called a unit if it has a two-sided inverse y, i.e.
    [Show full text]