DOCSLIB.ORG

Controlled Autonomous Vehicle Drift Maneuvering

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Controlled Autonomous Vehicle Drift Maneuvering Controlled Autonomous Vehicle Drift Maneuvering Thesis Presented in Partial Fulfillment of the Requirements for the Degree Master of Science in the Graduate School of The Ohio State University By Mohamed Lamine Kaba, B.S. Graduate Program in Electrical and Computer Engineering The Ohio State University 2019 Thesis Committee: Dr. Wei Zhang, Advisor Dr. Lisa Fiorentini c Copyright by Mohamed Lamine Kaba 2019 Abstract Drifting is an extreme maneuver which brings a vehicle into a relatively unstable and often hard to control configuration. Yet, it is an often necessary maneuver completed by profes- sional race car drivers; or to a limited extent, regular drivers aiming to regain control of their vehicle during bad road/weather conditions (e.g. vehicle skidding during snow). The study of autonomous vehicles during drifting can give insights into how to improve standard safety systems for both modern automobiles, as well as future autonomous vehicles, which must self-maneuver through such "obstacles". As complex as vehicle drifting is to maneuver, it is as complex (from a mathematical stand- point) to design drift trajectories/sequences for autonomous vehicles to track. The dynamic behavior of a vehicle during drifting is highly nonlinear; and nonlinear systems in general are typically hard to control. In this work, a set of scheduled linear controllers are used to give a vehicle the ability to autonomously drift itself about a globally planned path made using clothoids. This allows for the use of control methods such as LQR (Linear Quadratic Regulation) and PID (Proportional Integral Derivative) control in designing drift controllers capable of drifting and path following. The autonomous vehicle drifting algorithms are sim- ulated using MATLAB R /Simulink R . They are also tested on a modified 1:28 scale car, where a motion capture system is used for location tracking. Lastly, vehicle dynamics' system identification is covered in this work as well. ii This thesis is dedicated to my loving family. iii Acknowledgments I would like to express my gratitude to Prof. Zhang for having been my advisor over the course of this research, and for his teachings. His State-Space controls course solidified my interest in controls, and his approach to teaching the course (and in general) has funda- mentally changed the way in which I learn new information. I would also like to thank Prof. Fiorentini for taking time out of her schedule during a very busy week to be part of my thesis committee. Her feedback gave me a lot to think about in regards to future applications of this work. I would also like to thank Hao Yan for his collaboration on this project while he was completing his master's project. I enjoyed having a like-minded person to swap ideas with. Finally my mom, Oumou, for her endless sacrifices over the years which have allowed me to get where I am today. And to the rest of my family for their endless support of my endeavors. iv Vita December 2016 . B.S., Electrical and Computer Engineering, Ohio State University, Columbus, Ohio February 2017 - January 2018 . .Systems Engineer, Tata Consultancy Services, Auburn Hills, Michigan June 2018 - August 2018 . Research Assistant, Ohio State University, Columbus, Ohio Fields of Study Major Field: Electrical and Computer Engineering v Table of Contents Page Abstract........................................... ii Dedication......................................... iii Acknowledgments..................................... iv Vita.............................................v List of Figures ...................................... viii List of Tables .......................................x List of Abbreviations ..................................x Chapters 1 Introduction1 1.1 Background on Autonomous Vehicles...................... 1 1.1.1 The Need for Autonomous Vehicles................... 1 1.1.2 Levels of Autonomy ........................... 2 1.2 Motivation .................................... 4 1.3 Consulted Literature and Objective....................... 6 1.4 Thesis Work.................................... 9 1.5 Thesis Overview ................................. 10 2 Background Theory 11 2.1 Systems and Modeling Theory ......................... 11 2.1.1 Systems Theory ............................. 11 2.1.2 Systems Modeling ............................ 13 2.2 Modeling of Dynamical Systems......................... 14 2.2.1 Discretization............................... 16 2.3 Linear Systems.................................. 17 3 Vehicle Model 24 3.1 Vehicle Modeling Overview and Assumptions................. 27 3.2 Nonlinear Single Track Model Dynamics.................... 29 3.3 Tire Modeling................................... 32 3.3.1 Dugoff Tire Model............................ 35 3.3.2 Modified Fiala Tire Model........................ 36 3.4 Linear Vehicle Model............................... 40 vi 4 Control Systems Planning and Design 42 4.1 Path Trajectory Creation ............................ 42 4.2 Vehicle Dynamics Equilibrium.......................... 46 4.2.1 Equilibrium Analysis Overview..................... 46 4.2.2 Phase Portrait .............................. 51 4.3 Controls Overview ................................ 56 4.3.1 Tracking and Regulation......................... 56 4.4 Deviation Definitions and Control ....................... 61 4.4.1 Deviation Definitions........................... 61 4.4.2 Vehicle Controller ............................ 66 5 System Architecture and Identification 70 5.1 Vehicle Specifications............................... 71 5.2 Vehicle Architecture ............................... 73 5.3 System Identification............................... 78 5.3.1 Physical Parameters Identification ................... 81 5.3.2 Tire and Road Parameters Identification................ 83 5.3.3 Steering and Force Identification.................... 88 6 Experimentation 99 6.1 Simulation Overview............................... 99 6.2 Steady State Drifting............................... 101 6.3 Transient Drifting ................................ 103 7 Conclusion and Future Work 107 Bibliography 108 vii List of Figures Figure Page 1.1 Example of vehicle during drifting (Courtesy of: Borna Bevanda on Un- splash). ...................................... 5 1.2 Mixed open and closed loop transient drift [41]................. 7 1.3 Minimum time cornering through friction-circle acceleration planning [20].. 8 1.4 Steady state drifting (courtesy of [38])...................... 9 3.1 Vehicle inertial frame. Dashed line is parallel to x-axis of coordinate. 25 3.2 Vehicle's body frame. .............................. 26 3.3 Vehicle's tire frame contact patch. ....................... 26 3.4 Friction circle of longitudinal/lateral force Coupling ............. 33 3.5 Rear tire Fiala lateral force as critical slip angle, αcr, is varied. αcr;mx corre- sponds to maximum critical slip e.g. when ξ = 1................ 38 4.1 Generic clothoid map adapted from [24]. (Left) Path in x-y plane starting from origin. (Right) Curvature, κ, of path as arc length, s, increases.. 44 4.2 r and β over a sweep of steering angles, at Vx = 1:05 m=s........... 48 f r 4.3 Fy and Fy over a sweep of steering angles, at Vx = 1:05 m=s. 48 4.4 Longitudinal force equilibria over a sweep of steering angles, at Vx = 1:05 m=s. 49 ◦ 4.5 r−β phase dynamic when vx = 1:1 and δ = 5 , with marked equilibria. Red: Cornering, Blue: Counterclockwise drift, Green: Clockwise drift . 53 4.6 r and β fo Vx = 0:3; 0:6; 0:9 and 1:1 m=s. ................... 55 4.7 Combined path error (ela) and its components: orientation error (∆ ) and position error (e).................................. 65 4.8 Arbitrary clothoid map from 3 types of curvatures (straight, spiral and arc) 67 4.9 Vehicle control architecture............................ 68 5.1 Project's scaled vehicle (Side view)........................ 71 5.2 Project architecture................................ 73 5.3 Motive screenshot of OptiTrack system during object selection. 75 5.4 Three of 6 of our OptiTrack system's cameras. ................ 76 5.5 Vehicle center of mass balancing......................... 82 5.6 Raw OptiTrack data of vehicle location during a sample ramp steer maneuver. 85 viii 5.7 Yaw rate (r) estimated from OptiTrack yaw ( ) data. Blue: Finite difference estimation. Brown: Kalman filter estimation (using former).......... 85 5.8 Identified absolute front/rear lateral forces overlaid with Modified Fiala Model (Yellow), and cornering stiffness line (Orange). ............ 87 5.9 Identified force coefficients over multiple wr runs. Vertical line correspond to trimmed average of a given coefficient...................... 92 5.10 Vehicle trajectories at fixed steering signals versus fitted radius of trajectory. 94 5.11 Radius fit for multiple input Arduino signals (hence steering angles) super- imposed....................................... 94 5.12 Fit of Arduino signal ws to steering angle (degrees) using piece-wise linear and quadratic fit, respectively........................... 95 5.13 Less accurate linear fit of Arduino signal ws to steering angle (degrees). 96 6.1 Vehicle dynamics simulation. .......................... 100 6.2 Vehicle dynamics inner control system overview. 100 6.3 Vehicle model started near drifting equilibrium at open loop. 101 6.4 Induced vehicle drift................................ 102 6.5 Project's clothoid testing map. ......................... 103 6.6 Resulting vehicle drift in simulation....................... 104 6.7 Drifting test on scaled vehicle..........................
Load more

Recommended publications
  • Six Adventure Road Trips
    Easy Drives, Big Fun, and Planning Tips Six Adventure Road Trips DAY HIKES, FLY-FISHING, SKIING, HISTORIC SITES, AND MUCH MORE A custom guidebook in partnership with Montana Offi ce of Tourism and Business Development and Outside Magazine Montana Contents is the perfect place for road tripping. There are 3 Glacier Country miles and miles of open roads. The landscape is stunning and varied. And its towns are welcoming 6 Roaming the National Forests and alluring, with imaginative hotels, restaurants, and breweries operated by friendly locals. 8 Montana’s Mountain Yellowstone and Glacier National Parks are Biking Paradise the crown jewels, but the Big Sky state is filled with hundreds of equally awesome playgrounds 10 in which to mountain bike, trail run, hike, raft, Gateways to Yellowstone fish, horseback ride, and learn about the region’s rich history, dating back to the days of the 14 The Beauty of Little dinosaurs. And that’s just in summer. Come Bighorn Country winter, the state turns into a wonderland. The skiing and snowboarding are world-class, and the 16 Exploring Missouri state offers up everything from snowshoeing River Country and cross-country skiing to snowmobiling and hot springs. Among Montana’s star attractions 18 Montana on Tap are ten national forests, hundreds of streams, tons of state parks, and historic monuments like 20 Adventure Base Camps Little Bighorn Battlefield and the Lewis and Clark National Historic Trail. Whether it’s a family- 22 friendly hike or a peaceful river trip, there’s an Montana in Winter experience that will recharge your spirit around every corner in Montana.
    [Show full text]
  • Mountain Bike Trail Development Concept Plan
    Mountain Bike Trail Development Concept Plan Prepared by Rocky Trail Destination A division of Rocky Trail Entertainment Pty Ltd. ABN: 50 129 217 670 Address: 20 Kensington Place Mardi NSW 2259 Contact: [email protected] Ph 0403 090 952 In consultation with For: Lithgow City Council 2 Page Table of Contents 1 Project Brief ............................................................................................................................................. 6 1.1 Project Management ....................................................................................................................... 7 About Rocky Trail Destination .......................................................................................................... 7 Who we are ......................................................................................................................................... 7 What we do .......................................................................................................................................... 7 Key personnel and assets ................................................................................................................. 8 1.2 Project consultant .......................................................................................................................... 11 Project milestones 2020 .................................................................................................................. 11 2 Lithgow as a Mountain Bike Destination ...........................................................................................
    [Show full text]
  • 2021 FIA Motorsport Games: Drifting Cup – Sporting Regulations
    2021 FIA MSG: Drifting Cup Sporting Regulations – Approved by WMSC 05.03.2021 _________________________________________________________________________________________ 2021 FIA Motorsport Games: Drifting Cup – Sporting Regulations INTRODUCTION 3 GENERAL INFORMATION 3 COMPETITION DIVISIONS 1. COMPETITION PARTICIPANTS 3 2. COMPETITION CATEGORY 3 3. ENTRY PROCEDURE 4 3.1 COMPETITOR APPLICATIONS 4 3.2 COMPETITOR NATIONALITY 4 3.3 COMPETITOR ELIGIBILITY 4 4. FIA MOTORSPORT GAMES: DRIFTING CUP TITLE 4 5. FIA MOTORSPORT GAMES 5 COMPETITION OFFICIALS 6. COMPETITION OFFICIALS 5 6.1 STEWARDS 5 6.2 CLERK OF THE COURSE AND/OR RACE DIRECTOR 6 6.3 EVENT SECRETARY 6 6.4 TECHNICAL DELEGATE AND/OR CHIEF SCRUTINEER 6 6.5 JUDGES 6 PENALTIES 7. PENALTIES 7 GENERAL PROVISIONS 8. GENERAL PROVISIONS 8 9. COMPETITION NUMBERS AND ADVERTISING ON CARS 8 9.1 COMPETITION NUMBERS 8 9.2 COMPETITION BRANDING 8 9.3 ADVERTISING ON CARS 8 10. SAFETY 8 10.1 GENERAL SAFETY 8 10.2 TRACK CONTROL 9 11. INSURANCE 9 11.1 EVENT INSURANCE 9 11.2 PERSONAL INSURANCE 10 12. SIGNALIZATION 10 13. ADMINISTRATIVE CHECK 10 14. SCRUTINEERING 10 14.1 GENERAL SCRUNTINEERING PRACTICES AND REQUIREMENTS 10 14.2. NOISE RESTRICTIONS 11 COMPETITION 15. BRIEFING 11 16. PRACTICE 11 17. COMPETITION 12 __________________________________________________________________________________________________ Updated on: 12/02/2021 1/34 2021 FIA MSG: Drifting Cup Sporting Regulations – Approved by WMSC 05.03.2021 _________________________________________________________________________________________ 18. START LINE PROCEDURE 12 19. QUALIFICATION 13 19.1 QUALIFYING FORMAT 13 19.2 INITIATION DURING QUALIFYING 13 19.3 QUALIFYING SCORING 13 19.4 QUALIFYING JUDGING CRITERIA 14 19.5 FORCE MAJEURE 17 20. TANDEM BATTLES 17 20.1 ELIMINATION FORMAT 17 20.2 TANDEM JUDGING CRITERIA 17 20.3 INCOMPLETE TANDEM RUNS 18 20.4 PASSING 19 20.5 TANDEM INITIATION PROCEDURE 19 20.6 TANDEM COLLISIONS AND CONTACT 20 20.7 CAR SERVICE DURING TANDEM 21 20.8 TANDEM REPLAYS AND TELEMETRY 22 21.
    [Show full text]
  • Journal of Asia Cross Country Rally
    KYB TECHNICAL REVIEW No. 56 APR. 2018 Introduction Journal of Asia Cross Country Rally TANAKA Kazuhiro 1 Introduction attack racing. To compare, this would be like driving from Tokyo to Nagoya on general roads in a day of which the The Asia Cross Country Rally (hereinafter "AXCR") is section between Kanagawa and Shizuoka Prefectures is a South East Asia's largest four-/two-wheel rally raid race competition. certified by the International Automobile Federation (FIA) and the International Motorcycling Federation (FIM). Starting from the Kingdom of Thailand, partici- pants drive through its neighboring countries. The 2017 AXCR marked 22 years of history. This is a formal inter- national competition of this kind that is geographically closest to Japan and can be expected for the country to deliver a tremendous advertisement effect in the Asian region. Many Japanese teams with business strategies enter the rally, including those based on Japanese automo- bile manufacturers or four-wheel drive (4WD) vehicle related companies. Particularly in recent years, AXCR has seen a fierce battle for championships by international cars for emerging countries manufactured by various Photo 1 Bad road surface due to rainfall automobile makers. The participating teams have substan- tially raised their racing level in their rally vehicles with dramatically improved performance. From Japan, a lot of private teams also participate in the rally probably because 2 Position of Cross Country Rallies AXCR takes place during the summer holiday season in Japan and the costs incurred for participation is reason- Motorsports of four-wheel cars can be roughly classi- able. fied into three types: racing, rallying and trials.
    [Show full text]
  • Drifting Performance
    Racelogic Ltd Introduction Congratulations on your purchase and welcome to the worldwide DriftBox community. Drifting With your DriftBox you will be able to display and log your drifting performance. DriftBox also generates a performance related Drifting Score, which you can submit to the DriftBox website for inclusion in the worldwide DriftBox drifting league tables. See how your skills compare to other DriftBox users from around the world at www.driftbox.com Performance With DriftBox it is very easy to measure acceleration times, braking distances, quarter mile times and many more. There are a number of configurable screens that show specific test results such as 0-60, 0-100, 0-100-0, ½ mile and ¼ mile etc. DriftBox is based on the Racelogic VBOX, which is used by the majority of Car Manufacturers, Tyre Manufacturers and car magazines around the world to assess performance. Because it is very easy to edit the test ranges, DriftBox is a very powerful tool for use in many different kinds of vehicle testing. - 1 - Racelogic Ltd Introduction Lap Timing Displaying your Lap times as you drive around a circuit is simple with DriftBox. You can display your last and best Lap times and Lap count, and also display split times for up to six specified split points around the lap. Through the DriftBox website and forum you are able to download circuit overlays from around the world, compare lap times, and share lap overlay data with other users. Speed Display DriftBox has a display screen mode that shows a large digital speed value and compass. In open conditions, DriftBox has a velocity accuracy of 0.1km/h, which is useful for checking the accuracy of your vehicle’s speedometer.
    [Show full text]
  • High-Speed Autonomous Drifting with Deep Reinforcement Learning
    1 High-speed Autonomous Drifting with Deep Reinforcement Learning Peide Cai∗1, Xiaodong Mei∗1, Lei Tai2, Yuxiang Sun1, and Ming Liu1 Abstract—Drifting is a complicated task for autonomous ve- hicle control. Most traditional methods in this area are based on motion equations derived by the understanding of vehicle dynamics, which is difficult to be modeled precisely. We propose a robust drift controller without explicit motion equations, v which is based on the latest model-free deep reinforcement β learning algorithm soft actor-critic. The drift control problem (a) Drifting through a corner (b) Normal driving through a corner is formulated as a trajectory following task, where the error- based state and reward are designed. After being trained on Fig. 1. Comparison between drifting and normal driving through a corner. A tracks with different levels of difficulty, our controller is capable drift car usually has a large slip angle b with saturated rear tires caused by of making the vehicle drift through various sharp corners quickly oversteering, which is often evidenced by large amounts of tire smoke. and stably in the unseen map. The proposed controller is further shown to have excellent generalization ability, which can directly handle unseen vehicle types with different physical properties, dynamics to reduce lap time with high-speed sideslip cornering such as mass, tire friction, etc. for racing games. The results could further contribute to the understanding of aggressive driving techniques and extend the Index Terms—Deep reinforcement learning, deep learning in robotics and automation, racing car, motion control, field robots. operating envelope for autonomous vehicles.
    [Show full text]
  • The Complete Stories
    The Complete Stories by Franz Kafka a.b.e-book v3.0 / Notes at the end Back Cover : "An important book, valuable in itself and absolutely fascinating. The stories are dreamlike, allegorical, symbolic, parabolic, grotesque, ritualistic, nasty, lucent, extremely personal, ghoulishly detached, exquisitely comic. numinous and prophetic." -- New York Times "The Complete Stories is an encyclopedia of our insecurities and our brave attempts to oppose them." -- Anatole Broyard Franz Kafka wrote continuously and furiously throughout his short and intensely lived life, but only allowed a fraction of his work to be published during his lifetime. Shortly before his death at the age of forty, he instructed Max Brod, his friend and literary executor, to burn all his remaining works of fiction. Fortunately, Brod disobeyed. Page 1 The Complete Stories brings together all of Kafka's stories, from the classic tales such as "The Metamorphosis," "In the Penal Colony" and "The Hunger Artist" to less-known, shorter pieces and fragments Brod released after Kafka's death; with the exception of his three novels, the whole of Kafka's narrative work is included in this volume. The remarkable depth and breadth of his brilliant and probing imagination become even more evident when these stories are seen as a whole. This edition also features a fascinating introduction by John Updike, a chronology of Kafka's life, and a selected bibliography of critical writings about Kafka. Copyright © 1971 by Schocken Books Inc. All rights reserved under International and Pan-American Copyright Conventions. Published in the United States by Schocken Books Inc., New York. Distributed by Pantheon Books, a division of Random House, Inc., New York.
    [Show full text]
  • First-Time Snowboarders D/02
    D/01 Section D - teaching beginner snowboarders In this chapter we 12 will explore... An example progression for first-timers. All first time lessons should begin on flat terrain, with as First-Time much space as possible and minimal traffic. Generic goals for any Snowboarders first-timer lesson include: staying safe whilst becoming familiar with the snowboard, learning Equipment intro, board how to move around mobility & basic stance on flat ground with one foot strapped in; learning Skating, gliding, climbing how to stop and change direction on both the heel and toe edge. Straight runs & direction changes (J-turns) The order of the following exercises will change relative to the available Two-footed orientation terrain and snow conditions, and your students’ physical ability, Side Slipping age and fitness. All of these exercises may not be needed in every lesson Floating leaf so make sensible decisions to maximise the students’ learning time. Lift riding CHAPTER 12 / FIRST-TIME SNOWBOARDERS D/02 Equipment intro, board mobility & basic stance What, why, how Getting to know the equipment (board, boots and bindings etc.), strapping the board on with one foot to get used to how it feels, and introducing an action-ready stance to use when snowboarding. To understand how to use equipment safely, to get comfortable balancing and moving around with the snowboard attached to the leading foot, and to build a stable position to move from when snowboarding. EQUIPMENT Start by checking everyone’s boots are tight enough. Hold the snowboard nose up so that the bindings are facing the group and introduce the nose and tail, toe and heel edges, then turn the snowboard over, base out, and explain the side-cut and edges.
    [Show full text]
  • Spirit Mountain Task Force
    SPIRIT MOUNTAIN TASK FORCE RECOMMENDATIONS MARCH 2021 0 SPIRIT MOUNTAIN TASK FORCE MEMBERS Co-Chairs: City Councilor Arik Forsman, Parks, Libraries and Authorities Chair City Councilor Janet Kennedy, Fifth District Task Force Members: Matt Baumgartner Amy Brooks Barbara Carr Michele Dressel Mark Emmel Daniel Hartman Hansi Johnson Noah Kramer Dale Lewis Sam Luoma Chris Rubesch Scott Youngdahl Aaron Stolp, Spirit Mountain Recreation Area Authority Board Chair Wayne DuPuis, an Indigenous representative with expertise in Indigenous cultural resources Ex officio members: Gretchen Ransom, Dave Wadsworth and Jane Kaiser (retired), directors at Spirit Mountain Anna Tanski, executive director of Visit Duluth Tim Miller and Bjorn Reed, representatives of the Spirit Mountain workforce selected in consultation with the AFSCME collective bargaining unit 1 CONTENTS Spirit Mountain Task Force Members ........................................................................................................................... 1 Introduction ................................................................................................................................................................... 3 Executive Summary ....................................................................................................................................................... 4 Fulfilling the Charge ....................................................................................................................................................... 5 Business
    [Show full text]
  • Rum Cay Article
    THEKITEBOARDER.COM The Best Kept Secret of the Bahamas Rum Cay: FROM REP TO DESIGNER: SLINGSHOt’S AMERY BERNARD MAKING A DIFFERENCE SOUTH OF THE BORDER HOT NEW PRODUCTS 23FOR 2011 THIS LIQUID IS FORCE SURF rider: JULIEN photo: SKIP BOARDS FILLION BANKS LIQUIDFORCEKITES.COM 2 THEKITEBOARDER.COM THEKITEBOARDER.COM 3 DEPARTMENTS Liquid Force 30 Close Up rider Jan Wainman Hawaii’s Spencer Lujan and North’s THEKITEBOARDER.COM Schiegnitz called Megan O’Leary. this session at Harmanus in 58 Designer’s Corner South Africa the Tech out with designers on seven new The Best Kept spring releases. best session of Secret of the Bahamas his life. Photo Rum Cay: 64 Analyze This Jens Hogenkamp TKB’s verdict on seven new 2011 products. FROM REP TO DESIGNER: SLINGSHOt’S AMERY BERNARD 71 Workbench MAKING A DIFFERENCE SOUTH OF THE BORDER Rider: Peter Schiebel HOT NEW PRODUCTS 23FOR 2011 Ghetto fixes to get you back on the water. Kirsty Jones grabs a surf session in Mauritius. Photo Ocean Therapy 5’10” TRESPASS 9M SPITFIRE 5’10” TRESPASS LAUNCH Zach Kleppe entertains the crowd with a particularly good wipeout. The new Kitehero Fin Mount is a solid way to attach your BOARD MOUNTS FEATURESGoPro to your twin tip. Photo Jim Stringfellow For mounting a GoPro to your twin tip, the all new Kitehero Fin Mount is a much safer and more secure alternative solution to GoPro’s adhesive disk mount. Utilizing the standard fin holes on virtually any kiteboard or wakeboard, the durable low profile plastic base gives riders an unobtrusive way to mount a camera to their deck.
    [Show full text]
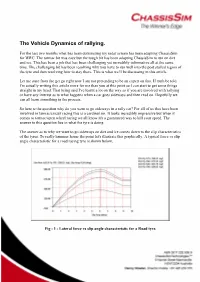
  • The Vehicle Dynamics of Rallying
    The Vehicle Dynamics of rallying. For the last two months what has been dominating my radar screen has been adapting ChassisSim for WRC. The tarmac bit was easy but the tough bit has been adapting ChassisSim to run on dirt and ice. This has been a job that has been challenging yet incredibly informative all at the same time. The challenging bit has been resolving why you have to run well into the post stalled region of the tyre and then resolving how to stay there. This is what we'll be discussing in this article. Let me state from the get go right now I am not pretending to be an expert on this. If truth be told I'm actually writing this article more for me than you at this point so I can start to get some things straight in my head. That being said I've learnt a lot on the way so if you are involved with rallying or have any interest as to what happens when a car goes sideways and then read on. Hopefully we can all learn something in the process. So here is the question why do you want to go sideways in a rally car? For all of us that have been involved in tarmac/circuit racing this is a cardinal sin. It looks incredibly impressive but when it comes to tarmac/open wheel racing we all know it's a guaranteed way to kill your speed. The answer to this question lies in what the tyre is doing. The answer as to why we want to go sideways on dirt and ice comes down to the slip characteristics of the tyres.
    [Show full text]
  • CANBERRA MOUNTAIN BIKE REPORT Draft December 2019
    N CANBERRA MOUNTAIN BIKE REPORT Draft December 2019 Prepared by The Canberra Mountain Bike Report has been prepared by TRC Tourism Pty Ltd for ACT Parks and Conservation Service. Acknowledgements We acknowledge the Traditional Custodians of the ACT, the Ngunnawal people. We acknowledge and respect their continuing culture and the contribution they make to the life of Canberra and the region. TRC Tourism would also like to acknowledge the contribution of the many stakeholders involved in this project, particularly the Project Reference Group: Rod Griffiths, National Parks Association, Jake Hannah, Majura Pines Trail Alliance, Mic Longhurst, Dynamic Motivation, Raynie McNee, Cycle Education, Lisa Morisset, Mountain Bike Australia, Kelly Ryan, Visit Canberra, Darren Stewart CORC, Jeff VanAalst, Stromlo Forest Park, Alan Vogt, Kowalski Brothers, Ryan Walsch, Fixed by Ryan and Claire Whiteman. Images: Courtesy of ACT Government, Spring Photo Competition, credits shown with image Front Cover Photos: Spring Photo Competition ACT Government (see credits in document) Map Design: TRC Tourism and Alan Vogt Disclaimer Any representation, statement, opinion or advice, expressed or implied in this document is made in good faith and on the basis that TRC Tourism Pty Ltd is not liable to any person for any damage or loss whatsoever which has occurred or may occur in relation to that person taking or not taking action in respect of any representation, statement or advice referred to in this document. www.trctourism.com DRAFT Canberra Mountain Bike Report| December 2019 i Contents Executive Summary v 1 Introduction 1 2 Strategic Context 5 3 The Mountain Bike Tourism Market 9 4 The Characteristics of Mountain Bikers 15 5 What Makes a Successful Mountain Bike Destination? 21 6 Canberra as a Mountain Bike Destination 24 7 Investing in New Trails - Potential Locations 43 8 The Canberra Mountain Bike Report 60 9 A Sustainable Management Model for the ACT 70 10 Benefits of the Report 75 11 Conclusion 79 Appendices 80 a.
    [Show full text]