DOCSLIB.ORG

Bandwidth Limitations of Ultra High Frequency–Radio Frequency

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bandwidth Limitations of Ultra High Frequency–Radio Frequency www.ietdl.org Published in IET Microwaves, Antennas & Propagation Received on 20th November 2012 Revised on 3rd May 2013 Accepted on 19th May 2013 doi: 10.1049/iet-map.2013.0158 ISSN 1751-8725 Bandwidth limitations of ultra high frequency–radio frequency identification tags Gerard Zamora1, Ferran Paredes1, Francisco Javier Herraiz-Martínez2, Ferran Martín1, Jordi Bonache1 1GEMMA/CIMITEC, Departament d’Enginyeria Electrònica, Universitat Autònoma de Barcelona, 08193 Bellaterra (Barcelona), Spain 2Department of Signal Theory and Communications, Carlos III University in Madrid, Leganés (Madrid), 28911, Spain E-mail: [email protected] Abstract: Fundamental bandwidth limitations on the design of ultra high frequency (UHF) radio frequency identification (RFID) tags are investigated. This study was conducted by considering the optimum equivalent-circuit network necessary for bandwidth broadening in single resonant UHF–RFID tags with conjugate matching. This equivalent-circuit network is simply a parallel combination of an inductor and a resistor cascaded to the UHF–RFID chip. Bandwidth optimisation of the resulting network is validated by means of the Bode criterion. According to this analysis, a broadband UHF–RFID tag prototype able to operate worldwide is designed and fabricated. In order to reduce tag size and cost, the external matching network is omitted in the reported implementation. The measured read ranges are above 5 m within the whole UHF–RFID frequency band (840– 960 MHz), with a peak value of 9 m at 870 MHz. 1 Introduction reader can read information from the tag. Since the impedance of RFID chips is complex and depends on the Radio frequency identification (RFID) is a rapidly developing manufacturer, specific RFID tag antennas must be designed technology that provides wireless identification and tracking for the considered chips available on the market. RFID tags capability [1]. Although the first paper on the basic are typically designed to achieve conjugate matching principles of passive RFID technology was published in between the chip and the antenna (this maximises the read 1948 [2], it took a long time before the technology range). Several techniques for achieving complex advanced to the current level [3]. Nowadays, many impedance matching by means of matching networks can applications, such as electronic toll collection, asset be found in the literature [6–8]. In [8], matching at two of identification, retail item management, access control, the UHF–RFID regulated bands (Europe and USA) was animal tracking and vehicle security, among others, require considered, and it was demonstrated that optimum matching RFID systems [4]. can be achieved by using dual-band tags, rather than A passive back-scattered RFID system consists of a reader broadband ones. Nevertheless these matching networks and a tag, which includes an antenna and an application introduce losses, which may degrade the tag performance. specific integrated circuit (ASIC) chip. The reader transmits However, apart from the losses introduced by the matching a modulated signal with periods of un-modulated carrier, network, cost and size issues sometimes force to omit which is received by the tag antenna. The chip converts the external matching networks and direct matching between un-modulated signal to DC (for external feeding) and sends the antenna and the chip is a due. back its information by varying its complex RF input The qualitative behaviour of antenna impedance, chip impedance. This impedance typically toggles between two impedance and read range as a function of frequency for a different states, corresponding to conjugate matching and to typical UHF–RFID tag is illustrated in Fig. 1 [5]. It can be some other impedance, effectively modulating the seen that chip impedance is always capacitive and has a back-scattered signal [5]. The UHF–RFID regulated bands small resistance [9, 10]. Obviously, this complex impedance vary in the different world regions, and include frequencies is frequency dependent, and adds difficulty in obtaining between 840 and 960 MHz. Thus, UHF–RFID is operated broadband matching with simple matching networks or at 840–845 MHz in China, at 866–869 MHz in Europe, at without matching networks. For this reason, the design of 902–928 MHz in USA and at 950–956 MHz in Japan. worldwide UHF–RFID tags without external matching Appropriate impedance matching between the antenna and networks represents an important challenge in RFID the chip is of substantial importance in RFID [5]. It directly technology. influences RFID system performance, such as the read In this paper, we investigate the fundamental bandwidth range of the tag, that is, the maximum distance at which a limitations on the design of single resonant UHF–RFID 788 IET Microw. Antennas Propag., 2013, Vol. 7, Iss. 10, pp. 788–794 & The Institution of Engineering and Technology 2013 doi: 10.1049/iet-map.2013.0158 www.ietdl.org Fig. 1 Antenna impedance, chip impedance and read range as functions of frequency for a typical RFID tag Fig. extracted from [5] tags with complex conjugate matching at roughly the where s denotes the reflection coefficient, ω the angular intermediate frequency of the UHF–RFID worldwide band frequency and RC and CC are the equivalent resistance and (915 MHz). According to this analysis, we also propose a capacitance, respectively, of the chip. Since ln(1/|s|) can be broadband tag exhibiting conjugate matching at this expressed in terms of the return loss (in dB) at the input of frequency, without using an external matching network. the matching network, the expression (1) yields The presented tag operates worldwide, with a significant read range ( >5 m) within the whole UHF–RFID band 1 (840–960 MHz), and a peak value of 9 m. − || ≤ 10 log e s dBdf (2) RCCC 2 Physical bandwidth limitations and 0 optimisation Expression (2) forces the area given by the return loss curve to 2.1 Bode criterion be less than, or equal, to a constant. Bandwidth optimisation implies assuming |s| to be a constant over the band of interest, – The input impedance of a UHF RFID chip is mainly and |˙s|=1 (RL = 0 dB) elsewhere. This is the response with determined by the voltage multiplier stage of the integrated maximum bandwidth, but it cannot be realised in practice circuit transponder, which can be modelled by a parallel because it would require an infinite number of elements in combination of a resistance RC (that accounts for the losses the matching network [13]. The necessity of multiple stages of the multiplier) and a capacitance CC (that includes all the to approximate the optimum response makes this objective capacitive effects) [9, 10], as it is shown in Fig. 2. prohibitive because of the increment of cost and tag According to Bode’s limit [11, 12], the reflection dimensions. In fact, UHF–RFID tags are typically designed coefficient achievable by any passive and lossless network with a single resonant frequency in their frequency placed between a purely resistive generator and an RC response. Therefore in this work, the main objective is parallel load is limited by bandwidth optimisation by considering a single resonant UHF–RFID tag with complex conjugate matching at the 1 intermediate frequency. p 1 v ≤ ln || d (1) s RCCC 0 2.2 Choice of passive circuit network for conjugate matching and bandwidth optimisation The purpose of this subsection is to obtain the passive circuit network which provides complex conjugate matching at the intermediate frequency and the broader possible bandwidth when it is cascaded to a given UHF–RFID chip. Let us consider the schematic depicted in Fig 2, where the load to be matched consists of a parallel combination of a capacitance CC and a resistance RC. An eventual impedance matching network is inserted between the antenna and the Fig. 2 Schematic of a typical UHF–RFID tag in the most general load, to consider the most general case. Maximum power case transfer between the antenna and the chip is achieved for = ∗ = ∗ An impedance matching network is located in between the chip (modelled as conjugate matching, that is, Zchip ZN (or Ychip YN ), a RC parallel load) and the tag antenna since this forces the power reflection coefficient, given by IET Microw. Antennas Propag., 2013, Vol. 7, Iss. 10, pp. 788–794 789 doi: 10.1049/iet-map.2013.0158 & The Institution of Engineering and Technology 2013 www.ietdl.org the authors of [14, 15] the antenna or the antenna plus the matching network (see Fig. 2) for maximum bandwidth. 2 It is important to point out that a series combination of an ∗ 2 ∗ 2 − + 2 Z −Z Y −Y GN Gchip B inductor and a resistor cascaded to the chip, providing ||s 2= chip N = N chip =(3) + + 2 conjugate matching at f , can be considered to achieve a Zchip ZN YN Ychip + + 2 0 GN Gchip B bandwidth very close to the optimum. This is a direct consequence of the fact that a low-loss network is required to be zero. In (3), YN = GN +jBN, Ychip = Gchip +jBchip and B = for bandwidth optimisation. In order to demonstrate it, let BN + Bchip. Since the chip impedance depends on the input us consider a low-loss network formed by a series power applied to the chip [5], for the evaluation of the combination of a resistor with resistance Rs and an inductor χ ≫ x ≫ maximum read range, Zchip must be considered at the with reactance s (Q 1, therefore s Rs). The threshold power. conductance GN and susceptance BN of such a network can Obviously, conjugate matching cannot be fulfilled in a be approximated by broad band. Therefore we choose the intermediate – R R frequency of the UHF RFID frequency span, f0, to force G = s ≃ s (6) N 2 + x2 x2 conjugate matching. This means that the conductances and Rs s s susceptances must satisfy GN = Gchip and BN = −Bchip, fl −x −1 respectively, at f0.
Load more

Recommended publications
  • AM Series AGILE MODULATOR
    AM Series AGILE MODULATOR AM series is a family of frequency-agile analog audio/video modulators. AM-60-860, the flag-ship model, is available in NTSC C channels 2-135 (54-860 MHz), and the PAL B, G, and I channels in the same frequency range. A More economical models are available in NTSC for the frequency ranges 54-550 MHz, or 54-806 MHz. EAS (Emergency Alert System) is standard on all models. Stereo Audio, SAP (Secondary Audio Programming), and several other optional T features are also available. V Baseband Audio/Video P R O D U Modulated C Analog RF T S Ordering Information Model Stock # Description AM-60-860 59415A Frequency-agile Audio/Video Modulator, +60 dBmV, 54-860 MHz (NTSC) AM-60-806 59419 Frequency-agile Audio/Video Modulator, +60 dBmV, 54-806 MHz (NTSC) AM-60-550 59416 Frequency-agile Audio/Video Modulator, +60 dBmV, 54-550 MHz (NTSC) AM-45-550 59404 Frequency-agile Audio/Video Modulator, +45 dBmV, 54-550 MHz (NTSC) Options AM-OPT-02 BNC Video Input Connector AM-OPT-04 Sub-Band Output (Available with AM-60-550 only) AM-OPT-05 Integrated BTSC Stereo Audio AM-OPT-06 SAP Audio/ BTSC Stereo (Available with AM-60-860 only) products AM-OPT-07 Video AGC CATV AM-OPT-09 Balanced Audio Input, 600 Ohm (Standard on AM-60-860) Related Products Model Description AMCM Frequency-agile Audio/Video modulator, +45 dBmV, 54-860 MHz (NTSC & PAL), Twelve modulators in 2RU modulators freq. agile ACM Frequency-agile Audio/Video modulator, +45 dBmV, 54-806 MHz (NTSC only), Twelve modulators in 2RU MICM Fixed-channel Audio/Video modulator, +45 dBmV, 54-806 MHz (NTSC & PAL), Twelve modulators in 2RU www.blondertongue.com | 800-523-6049 76 Specifications Input Output Connector Connector: “F” Female Standard: “F” Female Impedance: 75 Ω Option 2: BNC Female Impedance: 75 Ω Return Loss: 12 dB Return Loss: 18 dB Frequency Range Video Input Level AM-60-860 Model: 54 to 860 MHz (NTSC CATV Ch.
    [Show full text]
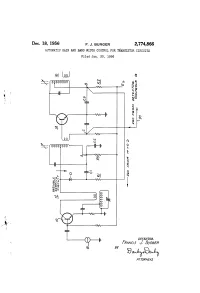
  • Dec. 18, 1956 . F. J. BURGER 2,774,866 Firancis. J. B/RGER
    Dec. 18, 1956 . F. J. BURGER 2,774,866 AUTOMATIC GAIN AND BAND WIDTH CONTROL FORTRANSISTOR CIRCUITS Filed Jan. 30, 1956 s log 00 0 0-0 000 & S. l INVENTOR, firANCIS. J. B/RGER 9. BY alid. A77ORNEYs 2,774,866 United States Patent Office Patented Dec. 18, 1956 2 reduced gain conditions. In order to prevent such dis tortion some means is required to reduce the signal level 2,774,866 prior to its application to the first intermediate frequency stage. In addition to the distortion problem, as is known, AUTOMATIC GAN AND BAND WIDTH CONTROL 5 the band width of the intermediate frequency amplifier FORTRANSISTOR CIRCUITS varies as a function of the magnitude of the automatic Francis J. Burger, Leonia, N. J., assignior to Enuerson gain controi voltage. As the gain of the transistor is Radio & Phonograph Corporation, Jersey City, N. , reduced, the loading which it presents to the intermediate a corporation of New York frequency coils decreases, thus increasing the Q of the O circuit and narrowing the band width. There also results Application January 30, 1956, Serial No. 562,072 a change in reactive loading provided by the I. F. tran 6 Claims. (C. 250-20) sistor which causes the intermediate frequency coils to shift their frequency center to a higher value. The purpose of this invention is to provide a variable This invention relates to improvements in transistor damping system which will vary the primary damping circuits, particularly transistor radio receivers with re of the converter intermediate frequency coil as a func spect to means for providing automatic gain and band tion of the automatic gain control voltage.
    [Show full text]
  • En 300 720 V2.1.0 (2015-12)
    Draft ETSI EN 300 720 V2.1.0 (2015-12) HARMONISED EUROPEAN STANDARD Ultra-High Frequency (UHF) on-board vessels communications systems and equipment; Harmonised Standard covering the essential requirements of article 3.2 of the Directive 2014/53/EU 2 Draft ETSI EN 300 720 V2.1.0 (2015-12) Reference REN/ERM-TG26-136 Keywords Harmonised Standard, maritime, radio, UHF ETSI 650 Route des Lucioles F-06921 Sophia Antipolis Cedex - FRANCE Tel.: +33 4 92 94 42 00 Fax: +33 4 93 65 47 16 Siret N° 348 623 562 00017 - NAF 742 C Association à but non lucratif enregistrée à la Sous-Préfecture de Grasse (06) N° 7803/88 Important notice The present document can be downloaded from: http://www.etsi.org/standards-search The present document may be made available in electronic versions and/or in print. The content of any electronic and/or print versions of the present document shall not be modified without the prior written authorization of ETSI. In case of any existing or perceived difference in contents between such versions and/or in print, the only prevailing document is the print of the Portable Document Format (PDF) version kept on a specific network drive within ETSI Secretariat. Users of the present document should be aware that the document may be subject to revision or change of status. Information on the current status of this and other ETSI documents is available at http://portal.etsi.org/tb/status/status.asp If you find errors in the present document, please send your comment to one of the following services: https://portal.etsi.org/People/CommiteeSupportStaff.aspx Copyright Notification No part may be reproduced or utilized in any form or by any means, electronic or mechanical, including photocopying and microfilm except as authorized by written permission of ETSI.
    [Show full text]
  • Superheterodyne Receiver
    Superheterodyne Receiver The received RF-signals must transformed in a videosignal to get the wanted informations from the echoes. This transformation is made by a super heterodyne receiver. The main components of the typical superheterodyne receiver are shown on the following picture: Figure 1: Block diagram of a Superheterodyne The superheterodyne receiver changes the rf frequency into an easier to process lower IF- frequency. This IF- frequency will be amplified and demodulated to get a videosignal. The Figure shows a block diagram of a typical superheterodyne receiver. The RF-carrier comes in from the antenna and is applied to a filter. The output of the filter are only the frequencies of the desired frequency-band. These frequencies are applied to the mixer stage. The mixer also receives an input from the local oscillator. These two signals are beat together to obtain the IF through the process of heterodyning. There is a fixed difference in frequency between the local oscillator and the rf-signal at all times by tuning the local oscillator. This difference in frequency is the IF. this fixed difference an ganged tuning ensures a constant IF over the frequency range of the receiver. The IF-carrier is applied to the IF-amplifier. The amplified IF is then sent to the detector. The output of the detector is the video component of the input signal. Image-frequency Filter A low-noise RF amplifier stage ahead of the converter stage provides enough selectivity to reduce the image-frequency response by rejecting these unwanted signals and adds to the sensitivity of the receiver.
    [Show full text]
  • Lecture 15: Introduction to Mixers
    EECS 142 Lecture 15: Introduction to Mixers Prof. Ali M. Niknejad University of California, Berkeley Copyright c 2005 by Ali M. Niknejad A. M. Niknejad University of California, Berkeley EECS 142 Lecture 15 p. 1/22 – p. 1/22 Mixers IF RF RF IF LO LO An ideal mixer is usually drawn with a multiplier symbol A real mixer cannot be driven by arbitrary inputs. Instead one port, the “LO” port, is driven by an local oscillator with a fixed amplitude sinusoid. In a down-conversion mixer, the other input port is driven by the “RF” signal, and the output is at a lower IF intermediate frequency In an up-coversion mixer, the other input is the IF signal and the output is the RF signal A. M. Niknejad University of California, Berkeley EECS 142 Lecture 15 p. 2/22 – p. 2/22 Frequency Translation down- conv ers ion IF IFRF LO As shown above, an ideal mixer translates the modulation around one carrier to another. In a receiver, this is usually from a higher RF frequency to a lower IF frequency. In a transmitter, it’s the inverse. We know that an LTI circuit cannot perform frequency translation. Mixers can be realized with either time-varying circuits or non-linear circuits A. M. Niknejad University of California, Berkeley EECS 142 Lecture 15 p. 3/22 – p. 3/22 Ideal Multiplier Suppose that the input of the mixer is the RF and LO signal vRF = A(t) cos (ω0t + φ(t)) vLO = ALO cos (ωL0t) Recall the trigonometric identity cos(A + B) = cos A cos B − sin A sin B Applying the identity, we have vout = vRF × vLO A(t)ALO = {cos φ (cos(ωLO + ω0)t + cos(ωLO − ω0)t) 2 − sin φ (sin(ωLO + ω0)t + sin(ωLO − ω0)t)} A.
    [Show full text]
  • Intermediate Frequency (IF) Sampling Receiver Concepts
    ADC12DL040,ADC12DL065,ADC12DL080, ADC14L020,ADC14L040,CLC5903,LMH6550, LMH6551 Intermediate Frequency (IF) Sampling Receiver Concepts Literature Number: SNAA107 AnalogEdge_V4_Issue3 5/31/06 10:26 AM Page 1 ANALOG edge SM Expert tips, tricks, and techniques for analog designs Vol. IV, Issue 3 DESIGN idea Intermediate Frequency (IF) Sampling Receiver Concepts Mark Rives, Principal Applications Engineer his article will discuss Intermediate Frequency zone from 39 MHz to 78 MHz, it can still be recovered (IF) sampling concepts of sub-sampling (or but the absolute frequency information is lost. When the Tunder sampling), noise processing gain, and the input signal moves above Fs/2, it has been effects of interfering signals. Examples will be based on sub-sampled and ‘reflects’ or ‘folds’ at Fs/2 and moves the GSM/EDGE communications standard where the back toward 0 Hz at the ADC output. If Fs/2 = 39 MSPS, channel bandwidth is 200 kHz and the sample rate is an input signal at 40 MHz will fold back to 38 MHz. typically a multiple of 13 MHz. Folding will occur in each Nyquist zone. For example, a 244 MHz IF at 78 MSPS will result in a 10 MHz signal Sub-Sampling at the ADC output. The folded (or aliased) frequency is Nyquist’s sampling theorem states that if a signal is sampled calculated by finding the closest multiple of Fs to the at least twice as fast as the highest sampled frequency desired input frequency (FIN, 244 MHz), then subtracting component, no information will be lost when the signal is the two frequencies: reconstructed.
    [Show full text]
  • AP-60-860A Agile Processor
    AP-60-860A Agile Processor The AP-60-860A (Agile Digital/Analog Processor) operates in one of the three following modes: Mode 1: Analog Heterodyne Processor (Analog RF IN > Analog RF OUT) D Mode 2: Digital Heterodyne Processor (QAM IN > QAM OUT) I Mode 3: Digital-to-Analog Processor (8VSB or QAM IN > Analog RF OUT) G I Mode 1 Mode 2 Mode 3 T Analog RF QAM QAM/8VSB CATV Ch. T7-T13 A CATV Ch. 2-135 CATV Ch. 2-135 VHF Ch. 2-13 CATV Ch. T7-T13 VHF Ch. 2-13 L UHF Ch. 14-69 CATV Ch. 2-135 UHF Ch. 14-69 C O CATV Ch. 2-135 CATV Ch. 2-135 CATV Ch. 2-135 L L Analog RF QAM Analog RF E +60 dBmV +55 dBmV +60 dBmV C T Features I • As an agile analog heterodyne processor: accepts one Analog RF input (CATV sub-band channels T7-T13, CATV standard channels 2-135, VHF channels 2-13, and UHF channels 14-69) and delivers one Analog RF output (CATV standard channels 2-135) O • As an agile digital heterodyne processor: accepts one Digital Cable QAM input (CATV sub-band channels T7-T13, and CATV standard N channels 2-135) and delivers one Digital Cable QAM output (CATV standard channels 2-135) • As an agile digital-to-analog processor: accepts one Digital Off-air 8VSB or Digital Cable QAM input (CATV standard channels 2-135, VHF channels 2-13, and UHF channels 14-69) and delivers one Analog RF output (CATV standard channels 2-135) • Equipped with EAS interface which can also be used as an IF (Intermediate Frequency) input • Supports Closed Captioning (EIA-608) Ordering Information Model Stock # Description AP-60-860A 59819 Agile, Processor, +60 dBmV, 54-860 MHz output Related Products Model Description DAP Digital-to-Analog Processor; 1 RU AP Series Agile Heterodyne Processor; 1 RU Purchase from: www.multicominc.com 800-423-2594 407-331-7779 ® Rev.
    [Show full text]
  • Recommendation Itu-R Bo.650-2*,**
    Rec. ITU-R BO.650-2 1 RECOMMENDATION ITU-R BO.650-2*,** Standards for conventional television systems for satellite broadcasting in the channels defined by Appendix 30 of the Radio Regulations (1986-1990-1992) The ITU Radiocommunication Assembly, considering a) that the introduction of the broadcasting-satellite service offers the possibility of reducing the disparity between television standards throughout the world; b) that this introduction also provides an opportunity, through technological developments, for improving the quality and increasing the quantity and diversity of the services offered to the public; additionally, it is possible to take advantage of new technology to introduce time-division multiplex systems in which the high degree of commonality can lead to economic multi-standard receivers; c) that it will no doubt be necessary to retain 625-line and 525-line television systems; d) that broadcasting-satellite services are being introduced using analogue composite coding according to Annex 1 of Recommendation ITU-R BT.470 for the vision signal; e) that it is generally intended that broadcasting-satellite standards should facilitate the maximum utilization of existing terrestrial equipment, especially that which concerns individual and community reception media (receivers, cable, re-broadcasting methods of distribution etc.). For this purpose a unique baseband signal which is common to the satellite-broadcasting system and the terrestrial distribution network is desirable; f) that the requirements as regards sensitivity to interference of the systems that can be used were defined by Appendix 30 of the Radio Regulations (RR); g) that complete compatibility with existing receivers is in any event not possible for frequency-modulated satellite broadcasting transmissions; ____________________ * Note – The following Reports of the ITU-R were considered in relation with this Recommendation: ITU- R BT.624-4, ITU-R BO.632-4, ITU-R BS.795-3, ITU-R BT.802-3, ITU-R BO.953-2, ITU-R BO.954-2, ITU-R BO.1073-1, ITU-R BO.1074-1 and ITU-R BO.1228.
    [Show full text]
  • Operational Diagrams of Radio Transmitters & Receivers
    Operational Diagrams of Radio Transmitters & Receivers Professor Lance Breger and Professor Kenneth Markowitz TABLE OF CONTENTS Page Preface . 4 - 5 Introduction . 6. - 7 Operation of Adder-Antenna Transmitter . .9 Operation of AM Transmitter in General . 10. Operation of AM Transmitter Showing AM Modulator in Detail . 11 Operation of TRF AM Receiver . 12. Operation of Superheterodyne AM Receiver . 13 Operation of PM Transmitter . 14. Operation of FM Transmitter in General . 15 Operation of FM Transmitter with Indirect Modulation . 16. Operation of FM Transmitter with Direct Modulation . 17 Operation of FM Receiver . 18 - 19 Operation of PM Receiver . 20. Conclusion . 21. Copyright 2004 Lance Breger 3 PREFACE ● Students: M. B. Suranga Perera, Nikolay Ostrovskiy and Johnny Lam. They produced the professional The purpose of these diagrams is to graphically explain the overall operation of AM, PM, and graphics in these vector art diagrams and created the pages. FM communications systems using very little mathematics. This explanation is accomplished by tracing a simple sinusoidal signal through all stages of each system. Although students who are "mathematically To pay these students, the following persons or organizations at NYCCT generously offered financial challenged" will find these diagrams very helpful, most students who are beginning the study of electrical advice or funds: communications systems can benefit from these same diagrams. More advanced courses can also use ● Former Dean Phyllis Sperling of the School of Technology & Design
    [Show full text]
  • An Intermediate Frequency Amplifier for High-Temperature Applications
    1 An Intermediate Frequency Amplifier for High-Temperature Applications Muhammad Waqar Hussain, Hossein Elahipanah, Stephan Schroder,¨ Saul Rodriguez, Member, IEEE, Bengt Gunnar Malm, Senior Member, IEEE, Mikael Ostling,¨ Fellow, IEEE and Ana Rusu, Member, IEEE Abstract—This paper presents a two-stage small signal inter- their constituent GaN/SiC HEMTs. This maximum operating mediate frequency (IF) amplifier for high-temperature commu- temperature can be extended, in theory, to 500 ◦C by using nication systems. The proposed amplifier is implemented using our in-house developed 4H-SiC bipolar junction transistors in-house silicon carbide (SiC) bipolar technology. Measurements show that the proposed amplifier can operate from room tem- (BJTs) [10]. However, the temperature ratings of currently perature up to 251 ◦C. At a center frequency of 54.6 MHz, available commercial passives, especially capacitors, limits the the amplifier has a gain of 22 dB at room temperature which maximum operating temperature to around 250 ◦C. ◦ decreases gradually to 16 dB at 251 C. Throughout the measured Due to the relatively modest power gain of the current in- temperature range, it achieves an input and output return loss house SiC BJTs at high-temperature and high-frequencies, of less than -7 dB and -11 dB, respectively. The amplifier has a 1-dB output compression point of about 1.4 dBm, which remains we envision receiver topologies where the majority of the fairly constant with temperature. Each amplifier stage is biased receiver gain is provided at intermediate frequencies after with a collector current of 10 mA and a base-collector voltage down-converting the input signal.
    [Show full text]
  • Cable Technician Pocket Guide Subscriber Access Networks
    RD-24 CommScope Cable Technician Pocket Guide Subscriber Access Networks Document MX0398 Revision U © 2021 CommScope, Inc. All rights reserved. Trademarks ARRIS, the ARRIS logo, CommScope, and the CommScope logo are trademarks of CommScope, Inc. and/or its affiliates. All other trademarks are the property of their respective owners. E-2000 is a trademark of Diamond S.A. CommScope is not sponsored, affiliated or endorsed by Diamond S.A. No part of this content may be reproduced in any form or by any means or used to make any derivative work (such as translation, transformation, or adaptation) without written permission from CommScope, Inc and/or its affiliates ("CommScope"). CommScope reserves the right to revise or change this content from time to time without obligation on the part of CommScope to provide notification of such revision or change. CommScope provides this content without warranty of any kind, implied or expressed, including, but not limited to, the implied warranties of merchantability and fitness for a particular purpose. CommScope may make improvements or changes in the products or services described in this content at any time. The capabilities, system requirements and/or compatibility with third-party products described herein are subject to change without notice. ii CommScope, Inc. CommScope (NASDAQ: COMM) helps design, build and manage wired and wireless networks around the world. As a communications infrastructure leader, we shape the always-on networks of tomor- row. For more than 40 years, our global team of greater than 20,000 employees, innovators and technologists have empowered customers in all regions of the world to anticipate what's next and push the boundaries of what's possible.
    [Show full text]
  • Method of Aligning a Radio Receiver and Means for Indicating the Alignment of a Radio Receiver
    Europâisches Patentamt © European Patent Office @ Publication number: 0 003 634 Office européen des brevets Bl © EUROPEAN PATENT SPECIFICATION @ Date of publication of patent spécification: 07.1 0.81 (g) Int. Cl.3: H 04 B 1/26, H 03 J 3/14 @ Application number: 79300029.0 (g) Date offiling: 09.01 .79 (54) Method of aligning a radio receiver and means for indicating the alignment of a radio receiver. © Priority: 09.02.78 US 876386 @ Proprietor: MOTOROLA, INC. 1303 East Algonquin Road Schaumburg Illinois 60196 (US) (43) Date of publication of application: 22.08.79 Bulletin 79/1 7 @ Inventor: Gould, Larrie Alan 5622 Woodhollow @ Publication of the grant of the European patent: Arlington Texas 7601 6 (US) 07.10.81 Bulletin 81/40 Inventor: Reed, Kim Warren 6036 East Belknap FortWorth Texas 761 17 (US) @ Designated Contracting States: CH DE FR GB NL @ Représentative: Newens, Léonard Eric et aJ, F.J. CLEVELAND CO. 40/43 Chancery Lane © Références cited: London WC2A 1 JQ (GB) DE-A-2 624 787 DE-B-1 034 716 GB-A-559 555 US - A - 3 896 386 o 8 O Note: Within nine months from the publication of the mention of the grant of the European patent, any person may give notice to the European Patent Office of opposition to the European patent granted. Notice of opposition shall be filed in a written reasoned statement. It shall not be deemed to have been filed until the opposition fee has been m paid. (Art. 99(1 ) European patent convention). Courier Press, Leamington Spa, England.
    [Show full text]