No-Go Theorems and the Foundations of Quantum Physics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Introduction to Copyright and Licensing in an Open Access Environment
IOP publications Frequently asked questions Glossary Frequently asked questions Creative Commons Moral rights Creative Commons Assignment Open access Dealing with copyright works Introduction to copyright copyright.iop.org Introduction to Introduction open access environment access open copyright and licensing in an in licensing and copyright Introduction to copyright to Introduction works copyright with Dealing access Open Assignment Commons Creative Commons Creative questions asked Frequently Glossary questions asked Frequently publications IOP Moral rights rights Moral What is copyright? As soon as an idea is expressed in a physical medium, such as writing a paper, it qualifies for copyright protection. Copyright is a legal right that gives the copyright holder exclusive rights over how others use their work. The level and type of protection offered by copyright varies between countries. A form of intellectual property, copyright can be dealt with like other types of property – it can be acquired, disposed of or licensed. Copyright is time-limited. The period of protection varies, but in most countries a journal article created at the present time will be protected for between 50 and 70 years from the death of the last surviving author. By means of a number of local and international laws and conventions, copyright which arises in one country is recognised and protected in many others. Treatment of copyright in the digital environment is evolving at an unprecedented rate. Copyright exists to protect the rights of an owner of an original piece of work by imposing restrictions on reuse but it does not always fit well with how we use and share information in the digital sphere. -

Introductory Guide for Authors This Guide Is for Early-Career Researchers Who Are Beginning to Write Papers for Publication
Introductory guide for authors This guide is for early-career researchers who are beginning to write papers for publication. publishingsupport.iopscience.org publishingsupport.iopscience.org This guide is for early-career researchers who are beginning to write papers for publication. Academic publishing is rapidly changing, with new technologies and publication models giving authors much more choice over where and how to publish their work. Whether you are writing up the results of a PhD chapter or submitting your first paper, knowing how to prepare your work for publication is essential. This guide will provide an overview of academic publishing and advice on how to make the most of the process for sharing your research. For more information and to download a digital version of this guide go to publishingsupport.iopscience.org. c o n t e n t s Page Choosing where to submit your paper 4 Writing and formatting 6 Peer-review process 8 Revising and responding to referee reports 10 Acceptance and publication 12 Promoting your published work 13 Copyright and ethical integrity 14 Frequently asked questions 15 Publishing glossary 16 IOP publications 18 Introductory guide for authors 3 publishingsupport.iopscience.org Choosing where to submit your paper It can be tempting to begin writing a paper before giving much thought to where it might be published. However, choosing a journal to target before you begin to prepare your paper will enable you to tailor your writing to the journal’s audience and format your paper according to its specific guidelines, which you may find on the journal’s website. -

Journal Title Abbreviations
Journal Title Abbreviations A Accounts of Chemical Research Acta Chemica Scandinavica Acta Crystallographica Acta Crystallographica, Section A: Crystal Physics, Diffraction, Theoretical and General Crystallography Acta Crystallographica, Section B: Structural Acta Mathematica Academiae Scientiarum Hungaricae Crystallography and Crystal Chemistry Acta Metallurgica Acta Oto-Laryngologica Acta Physica Acta Physica Austriaca Acta Physica Polonica Acustica Advances in Applied Mechanics Advances in Atomic and Molecular Physics Advances in Chemical Physics Advances in Magnetic Resonance Advances in Physics Advances in Quantum Chemistry AIAA Journal AIChE Journal AIP Conference Proceedings Akusticheskii Zhurnal [Soviet Physics ‒ Acoustics] American Journal of Physics Analytical Chemistry Annalen der Physik (Leipzig) Annales de Chimie et de Physique Annales de Geophysique Annales de l'Institut Henri Poincare Annales de l'Institut Henri Poincare, Section A: Physique Annales de l'Institut Henri Poincare, Section B: Calcul des Theorique Probabilites et Statistique Annales de Physique (Paris) Annals of Fluid Dynamics Annals of Mathematics Annals of Otology, Rhinology, & Laryngology Annals of Physics (New York) Annual Review of Nuclear Science Applied Optics Applied Physics Letters Applied Spectroscopy Arkiv foer Fysik Astronomical Journal Astronomicheskii Zhurnal [Soviet Astronomy] Astronomische Nachrichten Astronomy and Astrophysics Astrophysical Journal Astrophysical Journal, Letters to the Editor Astrophysical Journal, Supplement Series Astrophysical -

Impact Factor Journals in Physics
Impact Factor Journals in Physics Indexed in ISI Web of Science (JCR SCI, 2019) ______________________________________________________________________________________________________________________ Compiled By: Arslan Sheikh In Charge Reference & Research Section Junaid Zaidi Library COMSATS University Islamabad Park Road, Islamabad-Pakistan. Cell: 92+321-9423071 [email protected] 2019 Impact Rank Journal Title Factor 1 REVIEWS OF MODERN PHYSICS 45.037 2 NATURE MATERIALS 38.663 3 Living Reviews in Relativity 35.429 4 Nature Photonics 31.241 5 ADVANCED MATERIALS 27.398 6 MATERIALS SCIENCE & ENGINEERING R-REPORTS 26.625 7 PHYSICS REPORTS-REVIEW SECTION OF PHYSICS LETTERS 25.798 8 Advanced Energy Materials 25.245 9 Nature Physics 19.256 10 Applied Physics Reviews 17.054 11 REPORTS ON PROGRESS IN PHYSICS 17.032 12 ADVANCED FUNCTIONAL MATERIALS 16.836 13 Nano Energy 16.602 14 ADVANCES IN PHYSICS 16.375 15 Annual Review of Fluid Mechanics 16.306 16 Annual Review of Condensed Matter Physics 14.833 17 PROGRESS IN PARTICLE AND NUCLEAR PHYSICS 13.421 18 Physical Review X 12.577 19 Nano-Micro Letters 12.264 20 Small 11.459 21 NANO LETTERS 11.238 22 Laser & Photonics Reviews 10.655 23 Materials Today Physics 10.443 24 SURFACE SCIENCE REPORTS 9.688 25 CURRENT OPINION IN SOLID STATE & MATERIALS SCIENCE 9.571 26 npj 2D Materials and Applications 9.324 27 PROGRESS IN NUCLEAR MAGNETIC RESONANCE SPECTROSCOPY 8.892 28 Annual Review of Nuclear and Particle Science 8.778 29 PHYSICAL REVIEW LETTERS 8.385 1 | P a g e Junaid Zaidi Library, COMSATS -

RMP Style Manual
Reviews of Modern Physics Style Guide Contents D. Use of the colon 15 E. Use of the apostrophe 15 I. Introduction 3 F. Use of exclamation points and italics 16 A. Note on LATEX 3 B. Note on REVTEX 3 XIV. Abbreviations and Acronyms 16 II. Preliminary Matter 3 XV. Units 16 A. Document header 3 B. Begin Document 4 XVI. Mathematical Material 17 C. Title 4 A. Characters 17 D. Author(s) and Affiliation(s) 4 1. Character fonts 17 E. Abstract 4 2. Diacritical signs 17 F. \maketitle 4 3. Subscripts and superscripts 17 G. Table of Contents 4 B. Abbreviations in math 18 1. Abbreviations designating mathematical III. Section Headings 5 functions 18 A. First subheading 5 2. Abbreviations in subscripts and superscripts 18 1. Second subheading 5 C. Mathematical expressions 18 1. When to display 18 IV. Numbering of Figures, Tables, and Equations 5 2. Punctuation 19 A. Figure numbering 5 3. Equation breaking (multilinear equations) 19 B. Table numbering 5 4. Equation numbering, special situations 19 C. Equation numbering 6 D. Bracketing 19 1. Grouping sequence 19 V. Acknowledgments 6 2. Specific bracket notation 19 VI. Lists of symbols and/or acronyms 6 3. Specialized bracket notation 20 E. Additional style guidelines 20 VII. Appendices 6 1. Placement of limits and indices 20 2. Fractions 20 VIII. Supplemental Material not in Appendices 7 3. Multiplication signs 20 4. Mathematical terms 20 IX. Style of References 7 5. Radical signs and overbars 20 A. Citations in the text 7 B. Citations in footnotes 7 XVII. The Production File 21 C. -

Style and Notation Guide
Physical Review Style and Notation Guide Instructions for correct notation and style in preparation of REVTEX compuscripts and conventional manuscripts Published by The American Physical Society First Edition July 1983 Revised February 1993 Compiled and edited by Minor Revision June 2005 Anne Waldron, Peggy Judd, and Valerie Miller Minor Revision June 2011 Copyright 1993, by The American Physical Society Permission is granted to quote from this journal with the customary acknowledgment of the source. To reprint a figure, table or other excerpt requires, in addition, the consent of one of the original authors and notification of APS. No copying fee is required when copies of articles are made for educational or research purposes by individuals or libraries (including those at government and industrial institutions). Republication or reproduction for sale of articles or abstracts in this journal is permitted only under license from APS; in addition, APS may require that permission also be obtained from one of the authors. Address inquiries to the APS Administrative Editor (Editorial Office, 1 Research Rd., Box 1000, Ridge, NY 11961). Physical Review Style and Notation Guide Anne Waldron, Peggy Judd, and Valerie Miller (Received: ) Contents I. INTRODUCTION 2 II. STYLE INSTRUCTIONS FOR PARTS OF A MANUSCRIPT 2 A. Title ..................................................... 2 B. Author(s) name(s) . 2 C. Author(s) affiliation(s) . 2 D. Receipt date . 2 E. Abstract . 2 F. Physics and Astronomy Classification Scheme (PACS) indexing codes . 2 G. Main body of the paper|sequential organization . 2 1. Types of headings and section-head numbers . 3 2. Reference, figure, and table numbering . 3 3. -
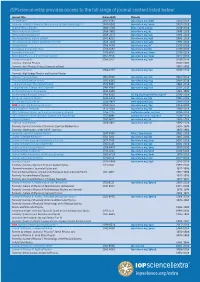
Iopscience Extra Content List
IOPscience extra provides access to the full range of journal content listed below: Journal Title Online ISSN Website 2D Materials 2 2053-1583 iopscience.org/2dm 2014–2018 Advances in Natural Sciences: Nanoscience and Nanotechnology 1, 2 2043-6262 iopscience.org/ansn 2010–2018 Applied Physics Express 1882-0786 http://apex.jsap.jp 2008–2018 The Astronomical Journal 2 1538-3881 iopscience.org/aj 1998–2018 The Astrophysical Journal 2 1538-4357 iopscience.org/apj 1996–2018 The Astrophysical Journal Letters 2 2041-8213 iopscience.org/apjl 1995–2018 The Astrophysical Journal Supplement Series 2 1538-4365 iopscience.org/apjs 1996–2018 Biofabrication 2 1758-5090 iopscience.org/bf 2009–2018 Bioinspiration & Biomimetics 2 1748-3190 iopscience.org/bb 2006–2018 Biomedical Materials 2 1748-605X iopscience.org/bmm 2006–2018 Biomedical Physics & Engineering Express 2 2057-1976 iopscience.org/bpex 2015–2018 Chinese Physics B 2058-3834 iopscience.org/cpb 2008–2018 Formerly: Chinese Physics 2000–2007 Formerly: Acta Physica Sinica (Overseas edition) 1992–1999 Chinese Physics C 2058-6132 iopscience.org/cpc 2008–2018 Formerly: High Energy Physics and Nuclear Physics Chinese Physics Letters 1741-3540 iopscience.org/cpl 1984–2018 Classical and Quantum Gravity 1361-6382 iopscience.org/cqg 1984–2018 Communications in Theoretical Physics 1572-9494 iopscience.org/ctp 1982–2018 Computational Science and Discovery 2 1749-4699 iopscience.org/csd 2008–2015 Distributed Systems Engineering 1361-6390 1993–1999 Environmental Research Letters 1, 2 1748-9326 erl.iop.org & -

Curriculum Vitae of Roderich Tumulka 1 Education and Employment 2
Curriculum vitae of Roderich Tumulka 1 Education and Employment Birthdate: 12 January 1972 Place: Frankfurt am Main, Germany Appointments Institution Dates Position Rutgers University 7/2010{present Associate Professor Rutgers University 7/2007{6/2010 Assistant Professor Eberhard-Karls-Universit¨at 12/2004{3/2007 Scientific Assistant T¨ubingen,Germany Postdoctoral Training, Visiting Positions, Etc. Institution Dates Title, Sponsor Eberhard-Karls-Universit¨at 7/2016{present Akademischer Rat T¨ubingen,Germany Eberhard-Karls-Universit¨at 4/2007{6/2007 Scholar, FQXi T¨ubingen,Germany IHES,´ Paris, France 2/2005{4/2005 Visiting Scientist Universit`adi Genova, Italy 5/2003{11/2004 Postdoc, Italian SF Rutgers University 9/2002{4/2003 Postdoc, German SF Ludwig-Maximilians-Universit¨at 11/2001{8/2002 Postdoc, German SF Munich, Germany Education and Degrees Institution Dates Degree Eberhard-Karls-Universit¨at 1/2008 Habilitation T¨ubingen,Germany Ludwig-Maximilians-Universit¨at 10/1998{10/2001 Doctor rerum naturalium Munich, Germany Johann-Wolfgang-Goethe-Univ. 10/1992{6/1998 Diplom-Mathematiker Frankfurt am Main, Germany 2 Publications Publications in peer-reviewed journals. 1. Sheldon Goldstein, Roderich Tumulka, and Nino Zangh`ı: \Is the hypothesis about a low entropy initial state of the universe necessary for explaining the arrow of time?," 13 pages. To appear in Physical Review D (2016) http://arxiv.org/abs/1602.05601 1 (According to researchgate.net, this article was the most read article from the Rutgers math department in the week of May 2, 2016.) 2. Sheldon Goldstein, Joel L. Lebowitz, Roderich Tumulka, and Nino Zangh`ı: \Any Orthonormal Basis in High Dimension is Uniformly Distributed over the Sphere," 22 pages. -

Abbreviations of Names of Serials
Abbreviations of Names of Serials This list gives the form of references used in Mathematical Reviews (MR). ∗ not previously listed The abbreviation is followed by the complete title, the place of publication x journal indexed cover-to-cover and other pertinent information. y monographic series Update date: January 30, 2018 4OR 4OR. A Quarterly Journal of Operations Research. Springer, Berlin. ISSN xActa Math. Appl. Sin. Engl. Ser. Acta Mathematicae Applicatae Sinica. English 1619-4500. Series. Springer, Heidelberg. ISSN 0168-9673. y 30o Col´oq.Bras. Mat. 30o Col´oquioBrasileiro de Matem´atica. [30th Brazilian xActa Math. Hungar. Acta Mathematica Hungarica. Akad. Kiad´o,Budapest. Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. ISSN 0236-5294. y Aastaraam. Eesti Mat. Selts Aastaraamat. Eesti Matemaatika Selts. [Annual. xActa Math. Sci. Ser. A Chin. Ed. Acta Mathematica Scientia. Series A. Shuxue Estonian Mathematical Society] Eesti Mat. Selts, Tartu. ISSN 1406-4316. Wuli Xuebao. Chinese Edition. Kexue Chubanshe (Science Press), Beijing. ISSN y Abel Symp. Abel Symposia. Springer, Heidelberg. ISSN 2193-2808. 1003-3998. y Abh. Akad. Wiss. G¨ottingenNeue Folge Abhandlungen der Akademie der xActa Math. Sci. Ser. B Engl. Ed. Acta Mathematica Scientia. Series B. English Wissenschaften zu G¨ottingen.Neue Folge. [Papers of the Academy of Sciences Edition. Sci. Press Beijing, Beijing. ISSN 0252-9602. in G¨ottingen.New Series] De Gruyter/Akademie Forschung, Berlin. ISSN 0930- xActa Math. Sin. (Engl. Ser.) Acta Mathematica Sinica (English Series). 4304. Springer, Berlin. ISSN 1439-8516. y Abh. Akad. Wiss. Hamburg Abhandlungen der Akademie der Wissenschaften xActa Math. Sinica (Chin. Ser.) Acta Mathematica Sinica. -

Reading List on Philosophy of Quantum Mechanics David Wallace, June 2018
Reading list on philosophy of quantum mechanics David Wallace, June 2018 1. Introduction .............................................................................................................................................. 2 2. Introductory and general readings in philosophy of quantum theory ..................................................... 4 3. Physics and math resources ...................................................................................................................... 5 4. The quantum measurement problem....................................................................................................... 7 4. Non-locality in quantum theory ................................................................................................................ 8 5. State-eliminativist hidden variable theories (aka Psi-epistemic theories) ............................................. 10 6. The Copenhagen interpretation and its descendants ............................................................................ 12 7. Decoherence ........................................................................................................................................... 15 8. The Everett interpretation (aka the Many-Worlds Theory) .................................................................... 17 9. The de Broglie-Bohm theory ................................................................................................................... 22 10. Dynamical-collapse theories ................................................................................................................ -

Scholarly Electronic Publishing Bibliography, Version 59
Scholarly Electronic Publishing Bibliography, Version 59 Item Type Book Authors Bailey, Charles W. Citation Scholarly Electronic Publishing Bibliography, Version 59 2005, Publisher University of Houston Libraries Download date 27/09/2021 19:27:27 Link to Item http://hdl.handle.net/10150/106410 SCHOLARLY ELECTRONIC PUBLISHING BIBLIOGRAPHY Version 59: 9/9/2005 Charles W. Bailey, Jr. University of Houston Libraries Scholarly Electronic Publishing Bibliography Charles W. Bailey, Jr. Acrobat version: http://info.lib.uh.edu/sepb/sepb.pdf HTML version: http://info.lib.uh.edu/sepb/sepb.html Included in the HTML version: Archive: http://info.lib.uh.edu/sepb/archive/sepa.htm Scholarly Electronic Publishing Resources: http://info.lib.uh.edu/sepb/sepr.htm Scholarly Electronic Publishing Weblog: http://info.lib.uh.edu/sepb/sepw.htm Copyright © 1996-2005 by Charles W. Bailey, Jr. This work is licensed under the Creative Commons Attribution-NonCommercial License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc/2.5/ or send a letter to Creative Commons, 543 Howard Street, 5th Floor, San Francisco, California, 94105, USA. University of Houston Library Administration 114 University Libraries Houston, TX 77204-2000 The author and the University of Houston Libraries make no warranty of any kind, either express or implied, for information in the Scholarly Electronic Publishing Bibliography, which is provided on an "as is" basis. The author and the University of Houston Libraries do not assume and hereby disclaim any liability to any party for any loss or damage resulting from the use of information in the Scholarly Electronic Publishing Bibliography. -

Journal of Physics a Mathematical and Theoretical
iopscience.org/jphysa Journal of Physics A Mathematical and Theoretical Highlights of 2011 Cover image: Artistic impression of nontrivial cycles and stabilizer code generators on a lattice from ‘Constructions and noise threshold of topological subsystem codes’ by M Suchara et al 2011 J. Phys. A: Math. Theor. 44 155301. Journal of Physics A: Mathematical and Theoretical Dear colleagues, 2011 has been another successful year for Journal of Physics A: Mathematical and Theoretical. The journal continues to have a broad audience and readers can enjoy high-quality research across theoretical and mathematical physics. This collection of highlights displays some of the most highly rated articles published in the journal during 2011. All of these articles were chosen primarily for their high-quality science. This selection displays the broad scope of the journal and demonstrates that it is a meeting place for researchers to share mathematically rich work across different disciplines. In 2011 we began to publish Insights: these are online, author-written news items highlighting the key achievements of recent work published in the journal to readers who might not be specialists in the field. All papers in this collection that have an associated Insight article are clearly marked. IMPACT FACTOR Some of our best articles have been published as Fast Track Communications (FTCs). FTCs * are short articles presenting important new developments in mathematical and theoretical 1.564 physics. FTCs benefit from accelerated publication and our recommended reader service, * As listed in ISI®’s 2011 Science Citation Index Journal Citation Reports where we will notify researchers selected by the authors when the article is published.