The Yang-Laplace Transform for Solving the Ivps with Local Fractional Derivative
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Research on Regional Economic Differences and Its Application
[Type text] ISSN : [Type0974 -text] 7435 Volume[Type 10 Issue text] 9 2014 BioTechnology An Indian Journal FULL PAPER BTAIJ, 10(9), 2014 [3321 - 3327] Research on regional economic differences and its application Chunguang Zhao*, Ying Hao College of Mathematics and Physics, Handan College, Handan 056005, (CHINA) E-mail : [email protected], [email protected] ABSTRACT This article takes 11 cities of Hebei Province as the object of study. According to Hebei Province's actual situation, we choose 6 important variables, which reflect the regional economies level of development. By analysing the data collected, the 11 regions of Hebei Province are divided into fourtypes: the developed, the more developed, the medium and the backward. And there is large differ-ence between the four types of regions. To further promote and realize coordinated development of theHebei Province economy, we should take measures to narrow the gap including making distinctive economic zone and business circle, promoting the regional harmonious development, developing the coastal economic belt and improving the underdeveloped region self-development capabilities. KEYWORDS Hebei province; Regional economies; Coordinated development; Principal components analysis; Cluster analysis. © Trade Science Inc. 3322 Research on regional economic differences and its application BTAIJ, 10(9) 2014 INTRODUCTION As the country continued to increase the pace of economic reform, Hebei Province, rapid economic development, economic strength and level has been among the ranks of the largest economy in the province[1]. However, economic development in Hebei province and there is a great gap between the economy, there are still many problems, especially in provincial cities between speed and level of economic development there is a clear imbalance, this imbalance has become Hebei Province, an important bottleneck restricting economic sustainable development. -

University Name Agency Number China Embassy in Tehran 3641
University Name Agency Number China Embassy in Tehran 3641 Aba Teachers College Agency Number 10646 Agricultural University of Hebei Agency Number 10086 Akzo vocational and technical College Agency Number 13093 Anglo-Chinese College Agency Number 12708 Anhui Agricultural University Agency Number 10364 Anhui Audit Vocational College Agency Number 13849 Anhui Broadcasting Movie And Television College Agency Number 13062 Anhui Business College of Vocational Technology Agency Number 12072 Anhui Business Vocational College Agency Number 13340 Anhui China-Australia Technology and Vocational College Agency Number 13341 Anhui College of Traditional Chinese Medicine Agency Number 10369 Anhui College of Traditional Chinese Medicine Agency Number 12924 Anhui Communications Vocational & Technical College Agency Number 12816 Anhui Eletrical Engineering Professional Technique College Agency Number 13336 Anhui Finance & Trade Vocational College Agency Number 13845 Anhui Foreign Language College Agency Number 13065 Anhui Industry Polytechnic Agency Number 13852 Anhui Institute of International Business Agency Number 13846 Anhui International Business and Economics College(AIBEC) Agency Number 12326 Anhui International Economy College Agency Number 14132 Anhui Lvhai Vocational College of Business Agency Number 14133 Anhui Medical College Agency Number 12925 Anhui Medical University Agency Number 10366 Anhui Normal University Agency Number 10370 Anhui Occupatinoal College of City Management Agency Number 13338 Anhui Police College Agency Number 13847 Anhui -

Analysis of the Regional Economic Differences and Coordinated Development Countermeasures in Hebei Province
Available online www.jocpr.com Journal of Chemical and Pharmaceutical Research, 2014, 6(7):1158-1163 ISSN : 0975-7384 Research Article CODEN(USA) : JCPRC5 Analysis of the regional economic differences and coordinated development countermeasures in Hebei province Chunguang Zhao and Ying Hao College of Mathematics and Physics, Handan College, Handan, China _____________________________________________________________________________________________ ABSTRACT This article takes 11 cities of Hebei Province as the object of study. According to Hebei Province's actual situation , we choose 6 important variables ,which reflect the regional economies level of development. By analysing the data collected ,the 11 regions of Hebei Province are divided into four types: the developed ,the more developed ,the medium and the backward. And there is large difference between the four types of regions. To further promote and realize coordinated development of the Hebei Province economy ,we should take measures to narrow the gap including making distinctive economic zone and business circle ,promoting the regional harmonious development , developing the coastal economic belt and improving the underdeveloped region self-development capabilities. Key words: Hebei Province; regional economies; coordinated development; principal components analysis; cluster analysis _____________________________________________________________________________________________ INTRODUCTION As the country continued to increase the pace of economic reform, Hebei Province, rapid economic development, economic strength and level has been among the ranks of the largest economy in the province[1].However, economic development in Hebei province and there is a great gap between the economy, there are still many problems, especially in provincial cities between speed and level of economic development there is a clear imbalance, this imbalance has become Hebei Province, an important bottleneck restricting economic sustainable development. -

From “Yung Wing's
Advances in Social Science, Education and Humanities Research, volume 416 4th International Conference on Culture, Education and Economic Development of Modern Society (ICCESE 2020) A Study on Library Development Practice and Thought of Notabilities Whose Native Places Are Xiangshan — From “Yung Wing’s Paper” to “Four- corner Indexing System” Xiaohui Zhang Library Zhuhai College of Jilin University Zhuhai, China 519000 Abstract—By studying documents such as "Yung Wing's significant contribution on the indexing of ancient books in Paper", Tsai Ting Kan's "Lao Jie Lao" (a book of annotation China. This article only discusses the library theory and of "Lao Tzu"), Zheng Guanying's "Shengshi Weiyan: practice from “Yung Wing’s Paper” to "Four-corner Number CangShu" (a book of exploring the way to save the country), Checking Method", and reveals the main academic and Wang Yunwu's "Four-corner Indexing System", the viewpoints and contributions of library industry in modern article selects the excellent practice of most famous sages of China. Xiangshan in Guangdong in library business, while extracting the essence of their ideas. From the perspective of literature analysis, it can be seen that notabilities whose native places are II. "YUNG WING'S PAPER" Xiangshan devoted a lot of effort to the library cause in In Yung Wing's residence in his old age, 16 Edwood modern China, which is of special value to the research and Road, Hartford City, he completed the English construction of the "Greater Bay Area with Humanities" of autobiography "My Life in China and America", which Xiangshan culture, and has special historical status in China's mentioned in Chapter 5 "My College Days" that, at the end library cause, deserving the attention of academic circles. -

A Complete Collection of Chinese Institutes and Universities For
Study in China——All China Universities All China Universities 2019.12 Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities Anhui 安徽 【www.studyinanhui.com】 1. Anhui University 安徽大学 http://ahu.admissions.cn 2. University of Science and Technology of China 中国科学技术大学 http://ustc.admissions.cn 3. Hefei University of Technology 合肥工业大学 http://hfut.admissions.cn 4. Anhui University of Technology 安徽工业大学 http://ahut.admissions.cn 5. Anhui University of Science and Technology 安徽理工大学 http://aust.admissions.cn 6. Anhui Engineering University 安徽工程大学 http://ahpu.admissions.cn 7. Anhui Agricultural University 安徽农业大学 http://ahau.admissions.cn 8. Anhui Medical University 安徽医科大学 http://ahmu.admissions.cn 9. Bengbu Medical College 蚌埠医学院 http://bbmc.admissions.cn 10. Wannan Medical College 皖南医学院 http://wnmc.admissions.cn 11. Anhui University of Chinese Medicine 安徽中医药大学 http://ahtcm.admissions.cn 12. Anhui Normal University 安徽师范大学 http://ahnu.admissions.cn 13. Fuyang Normal University 阜阳师范大学 http://fynu.admissions.cn 14. Anqing Teachers College 安庆师范大学 http://aqtc.admissions.cn 15. Huaibei Normal University 淮北师范大学 http://chnu.admissions.cn Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities 16. Huangshan University 黄山学院 http://hsu.admissions.cn 17. Western Anhui University 皖西学院 http://wxc.admissions.cn 18. Chuzhou University 滁州学院 http://chzu.admissions.cn 19. Anhui University of Finance & Economics 安徽财经大学 http://aufe.admissions.cn 20. Suzhou University 宿州学院 http://ahszu.admissions.cn 21. -

Phenyl Propenyl Acyloxy Alkyl Phosphonate Molecular Derivatives
Latin American Applied Research 44:137-140 (2014) STUDY ON STRUCTURE-ACTIVITY RELATIONSHIP OF 2E-3- PHENYL PROPENYL ACYLOXY ALKYL PHOSPHONATE MOLECULAR DERIVATIVES H.-M. BI†, P.-T. XIE†, J.-P. HU†, Y. LIU†, F.-Y. YOU† and L.-P. MENG‡ † Handan key laboratory of organic small molecule materials, Handan College, Hebei Handan 056002, China. [email protected] ‡ Hebei Normal University, Shijiazhuang, Hebei Province 050091, China Abstract— The quantum chemistry calculation of obtained. Harmonic vibrational frequencies calculated at 2E-3-phenyl propenyl acyloxy alkyl phosphonate the same level were used for the characterization of sta- derivates was carried out to investigate the relation- tionary points as a minimum. All quantum calculations ship between the structure and plant regulator activ- were performed with the Gaussian 03 program. The ity of these compounds. All the compounds were logP, V, M, Sg and Rm were calculated by Hyperchem studied by HF method with 6-31G* basis set using using the optimized configuration from the result of the PCM model within the self-consistent reaction Gaussian 03. field method to assess solvent effects, and then we es- tablished mathematical correlation between the B. Results and discussions properties and bioactivity of these compounds. The Stability configurations and natural charge result showed that the bioactivity of these com- Figure 1 depicts the structure of compounds. The atom- pounds has a linear relationship with the frontier ic natural charges of compounds are given in Table 1. orbital energy and other properties. At the same These data show that the negative charge is mainly con- time, the active sites of these molecules were predict- centrated in the C (8), and O (10) of carbonyl, These at- ed. -

Research Java Web Framework Based on Osgi
AvailableAvailable online online at www.sciencedirect.com at www.sciencedirect.com Procedia Engineering ProcediaProcedia Engineering Engineering 00 (2011) 15 (2011) 000–000 2374 – 2378 www.elsevier.com/locate/procedia Research Java Web framework based on OSGi Jingjun Zhanga, Lei Wangb, Hui Lic and Guangyuan Liub a* aDepartment of Science Research, Hebei University of Engineering, Handan, Hebei, 056038, China bHebei University of Engineering, Handan, Hebei, 056038, China c Handan College, Handan, Hebei, 056005, China Abstract OSGi (Open Services Gateway Initiative) provides a programming model for service components. Programming based on OSGi can bring many advantages, such as modular, standardized, service oriented, dynamisms, and easy reuse, easy extension, easy deployment, and so on. At this issue, we integrate the OSGi and Java Web popular framework which includes Struts, Spring, Hibernate, and build an enterprise applications micro-core architecture called OSSH. Java programmers who are familiar with SSH can experience the benefits of OSGi. Keywords: OSGi; Integration Framework; Java Web; 1. Introduction As the rapid development of hardware and network technology, the software features undoubtedly become more complex, larger, and its requirements change frequently because of the changing business environment. Software companies are facing a global size of the common problems which includes real- time response to new demands, the dynamic deployment of new modules, and rapid assembly of various components of the service [1]. OSGi (Open Service Gateway Initiative) makes all these questions simple. OSGi is an application development framework which is lightweight, loosely coupled, service-oriented [2]. OSGi modules bring a standardized development of organizations and unified way. The OSGi-based systems have many benefits including hot-swappable plug-in architecture, high reusability, efficiency, etc. -

CGS) Merupakan Beasiswa Full Untuk Meneruskan Jenjang Pendidikan Magister Di Shanghai Normal University Dari Tahun 2016 Sampai Dengan Saat Ini
Departemen Pendidikan dan Pengembangan Organisasi Perhimpunan Pelajar Indonesia (PPI) Tiongkok Beasiswa pertama yang ia peroleh dari Chinese Government Scholarships (CGS) merupakan beasiswa full untuk meneruskan jenjang pendidikan magister di Shanghai Normal University dari tahun 2016 sampai dengan saat ini. Belajar dan tinggal di negeri China merupakan cita-cita kecilnya semenjak usia 6 tahun. Karena ia terinspirasi dari hadits Nabi Muhammad SAW yang berbunyi, “Uthlubul ilma walau bisshin” yang artinya, “Carilah ilmu sampai ke negeri China”. 0 | H a l a m a n Departemen Pendidikan dan Pengembangan Organisasi Perhimpunan Pelajar Indonesia (PPI) Tiongkok 1 | H a l a m a n Departemen Pendidikan dan Pengembangan Organisasi Perhimpunan Pelajar Indonesia (PPI) Tiongkok PPI Tiongkok mempersembahkan PANDUAN KULIAH DI CHINA Edisi 2017 Penulis: Nurul Juliati Putra Wanda Ahmad Fahmi Putri Aris Safitri Tirta anhari Editor: Fadlan Muzakki, Sitti Marwah, Marilyn Janice 2 | H a l a m a n Departemen Pendidikan dan Pengembangan Organisasi Perhimpunan Pelajar Indonesia (PPI) Tiongkok Sambutan Ketua PPI Tiongkok Salam sejahtera untuk kita semua. Ada pepatah yang mengatakan hidup itu harus menjadi garam dan terang bagi dunia. atas dasar itulah PPI Tiongkok ada, yaitu memberikan kontribusi positif bagi Indonesia. PPI Tiongkok sebagai wadah pengembangan minat dan bakat mahasiswa Indonesia memegang peranan penting dalam mempersatukan para pelajar Indonesia di Tiongkok. salah satu misi kami adalah agar para pelajar Indonesia tidak lupa dengan bangsanya sendiri dan suatu saat nanti bisa pulang untuk membangun Indonesia. Oleh karena itu visi Kabinet KB (keluarga berencana) PPI Tiongkok tahun ini adalah memperkuat hubungan internal antar pengurus dan juga meningkatkan kesinergian antara PPIT Cabang. kami yakin dengan hubungan internal yang solid, bahkan hingga mampu menjadi seperti keluarga, ditambah dengan perencanaan yang matang, PPI Tiongkok dapat menghasilkan inisiatif-inisiatif yang dapat berdampak positif bagi mahasiswa-mahasiswa Indonesia yang ada di Tiongkok. -

Research on English and American Literature and English Teaching
2020 4th International Conference on Economics, Management Engineering and Education Technology (ICEMEET 2020) Research on English and American Literature and English Teaching Hongyan Zhou Shandong Youth University of Political Science, Jinan, Shandong, 250103, China Keywords: English and American literature, English teaching Abstract: British and American literature is an important part of the entire English teaching process and plays an important role in the entire English teaching. In the process of English teaching, with the introduction of British and American culture as the background and the appreciation of classic literary works as the teaching method, students can enhance their ability to appreciate and analyze works while reading and writing in English. By teaching the knowledge of English and American literature, it is possible to cultivate the comprehensive quality of students and comprehensively improve the quality of English teaching. 1. Introduction The status of British and American literature in English teaching is self-evident, but it has long been neglected in college English teaching. The reason is that there are few college English class hours, limited foreign language level of the students, and relatively weak teachers of college English teachers. However, the author believes that the root cause is still the education concept that emphasizes ability and light quality. Now when it comes to the reform of college English teaching, people think of strengthening the cultivation of students' listening, speaking, reading, writing and other application abilities. Our current college English education is too focused on the training of basic skills. It seems that there is nothing but listening, speaking, reading, writing and translating. -

Content • June 2016 • Issue 13 Research on Optimal Placement Of
Content • June 2016 • Issue 13 Research on Optimal Placement of Sensors in the Vibration Test of Hydropower House 5 Wang Liqing, Zhang Yanping, Henan Vocational College of Water and Environment, Zhengzhou, Henan, China Improvement of the Volume Data Segmentation and Visualization 11 Qian Xua, Zhengxu Zhao, Yang Guo, Shijiazhuang Tiedao University, Shijiazhuang, Hebei, China Feature Research on Aerobic Granular Sludge to Remove Saliferous Organic Wastewater 16 Gaoli Guo, Hubei University of Technology Engineering and Technology College, China; Bihua Xiong, Hubei Sunshine 100 Real Estate Co., Ltd; Hubei University of Technology Engineering and Technology College, China Research on the Modern Agricultural Informationization Construction Mode and Application in Sichuan Province, China 22 Jiangke Cheng, [email protected]; Shengnan Wang; Panzhihua University, Panzhihua, Sichuan Province, China Collaborative Strategies and Applied Research of Costume Design Supply Chains Based on Cloud Computing 28 Ran Duan, [email protected]; Xiaogang Liu; Fashion and Art Design Institute, Donghua University, Shanghai, China Research on the Relationship Between Pore Structure of PHCP Concrete and Its Sulfate Erosion Resistance 33 Yanyan Hu, [email protected]; Tingshu He; Collage of Materials and Mineral Resources, Xi’an University of Architecture and Technology, Xi’an, Shaanxi Province, China Evaluation of Undesirable Output of Regional Multi-airport Productivity 38 Wei Wei; College of Air Transportation, Shanghai University of Engineering Science, Shanghai, -
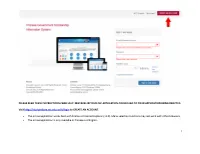
1 Please Read These Instructions Carefully
PLEASE READ THESE INSTRUCTIONS CAREFULLY. MISTAKES IN YOUR CSC APPLICATION COULD LEAD TO YOUR APPLICATION BEING REJECTED. Visit http://studyinchina.csc.edu.cn/#/login to CREATE AN ACCOUNT. • The online application works best with Firefox or Internet Explorer (11.0). Menu selection functions may not work with other browsers. • The online application is only available in Chinese and English. 1 • Please read this page carefully before clicking on the “Application online” tab to start your application. 2 • The Program Category is Type B. • The Agency No. matches the university you will be attending. See Appendix A for a list of the Chinese university agency numbers. • Use the + by each section to expand on that section of the form. 3 • Fill out your personal information accurately. o Make sure to have a valid passport at the time of your application. o Use the name and date of birth that are on your passport. Use the name on your passport for all correspondences with the CLIC office or Chinese institutions. o List Canadian as your Nationality, even if you have dual citizenship. Only Canadian citizens are eligible for CLIC support. o Enter the mailing address for where you want your admission documents to be sent under Permanent Address. Leave Current Address blank. Contact your home or host university coordinator to find out when you will receive your admission documents. Contact information for you home university CLIC liaison can be found here: http://clicstudyinchina.com/contact-us/ 4 • Fill out your Education and Employment History accurately. o For Highest Education enter your current degree studies. -

Century Journals Project (CJP)
China National Knowledge Infrastructure: Century Journals Project (CJP) Complete Title List - Series H (at July, 2008) Please note: Titles are sorted by Series, then Language (with English titles appearing first) , then by Pinyin title in English phonetic order. Earliest Control Journal Title Language Title in Pinyin Glossing of Title Former Title Freq. ISSN # CN # Publisher Issue in Status URL Notes Code Series CNKI H 当代中国人口 (英文版) English Dangdai Zhongguo Renkou (Yingwenban) China Population Today 当代中国人口 bimonthly 1003-4595 11-2872/C 中国人口信息研究 1994/01 Active http://china.eastview.com/kns50/Navi/Bridge.aspx?L DDZG H 上海体育学院学报 Chinese and Shanghai Tiyuxue Yuan Xue Bao Journal of Shanghai University of Sport bimonthly 1000-5498 31-1005/G8 上海体育学院 1959/01 Active http://china.eastview.com/kns50/Navi/Bridge.aspx?L STYB English H 山西农业大学学报 (社会科学版) Chinese and Shanxi Nongye Daxue Xuebao (Shehui Kexue Journal of Shanxi Agricultural University (Social quarterly 1671-816X 14-1305/C 山西农业大学 2002/01 Active http://china.eastview.com/kns50/Navi/Bridge.aspx?L SXND English Ban) Science Edition) H 英语知识 Chinese and Yingyu Zhishi The Knowledge of English monthly 1003-3351 21-1059/H 大连外国语学院 1987/01 Active http://china.eastview.com/kns50/Navi/Bridge.aspx?L YYZS English H 中国体育教练员 Chinese and Zhongguo Tiyu Jiaolianyuan China Sports Coaches quarterly 1006-8732 31-1644/G8 国家体育总局科教 1993/01 Active http://china.eastview.com/kns50/Navi/Bridge.aspx?L TYJL English H 安徽大学学报 (哲学社会科学版) Chinese Ahhui Daxue Xuebao (Zhexue Shehui Kexue Journal of Anhui University (Philosophy