Polynomial Transformations of Tschirnhaus, Bring and Jerrard
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

SIGLOG: Special Interest Group on Logic and Computation a Proposal
SIGLOG: Special Interest Group on Logic and Computation A Proposal Natarajan Shankar Computer Science Laboratory SRI International Menlo Park, CA Mar 21, 2014 SIGLOG: Executive Summary Logic is, and will continue to be, a central topic in computing. ACM has a core constituency with an interest in Logic and Computation (L&C), witnessed by 1 The many Turing Awards for work centrally in L&C 2 The ACM journal Transactions on Computational Logic 3 Several long-running conferences like LICS, CADE, CAV, ICLP, RTA, CSL, TACAS, and MFPS, and super-conferences like FLoC and ETAPS SIGLOG explores the connections between logic and computing covering theory, semantics, analysis, and synthesis. SIGLOG delivers value to its membership through the coordination of conferences, journals, newsletters, awards, and educational programs. SIGLOG enjoys significant synergies with several existing SIGs. Natarajan Shankar SIGLOG 2/9 Logic and Computation: Early Foundations Logicians like Alonzo Church, Kurt G¨odel, Alan Turing, John von Neumann, and Stephen Kleene have played a pioneering role in laying the foundation of computing. In the last 65 years, logic has become the calculus of computing underpinning the foundations of many diverse sub-fields. Natarajan Shankar SIGLOG 3/9 Logic and Computation: Turing Awardees Turing awardees for logic-related work include John McCarthy, Edsger Dijkstra, Dana Scott Michael Rabin, Tony Hoare Steve Cook, Robin Milner Amir Pnueli, Ed Clarke Allen Emerson Joseph Sifakis Leslie Lamport Natarajan Shankar SIGLOG 4/9 Interaction between SIGLOG and other SIGs Logic interacts in a significant way with AI (SIGAI), theory of computation (SIGACT), databases (SIGMOD) and knowledge bases (SIGKDD), programming languages (SIGPLAN), software engineering (SIGSOFT), computational biology (SIGBio), symbolic computing (SIGSAM), semantic web (SIGWEB), and hardware design (SIGDA and SIGARCH). -

© in This Web Service Cambridge University Press
Cambridge University Press 978-1-107-03903-2 - Modern Computer Algebra: Third Edition Joachim Von Zur Gathen and Jürgen Gerhard Index More information Index A page number is underlined (for example: 667) when it represents the definition or the main source of information about the index entry. For several key words that appear frequently only ranges of pages or the most important occurrences are indexed. AAECC ......................................... 21 analytic number theory . 508, 523, 532, 533, 652 Abbott,John .............................. 465, 734 AnalyticalEngine ............................... 312 Abel,NielsHenrik .............................. 373 Andrews, George Eyre . 644, 697, 729, 735 Abeliangroup ................................... 704 QueenAnne .................................... 219 Abramov, Serge˘ı Aleksandrovich (Abramov annihilating polynomial ......................... 341 SergeiAleksandroviq) 7, 641, 671, 675, annihilator, Ann( ) .............................. 343 734, 735 annusconfusionis· ................................ 83 Abramson, Michael . 738 Antoniou,Andreas ........................ 353, 735 Achilles ......................................... 162 Antoniszoon, Adrian (Metius) .................... 82 ACM . see Association for Computing Machinery Aoki,Kazumaro .......................... 542, 751 active attack . 580 Apéry, Roger . 671, 684, 697, 761 Adam,Charles .................................. 729 number ....................................... 684 Adams,DouglasNoël ..................... 729, 796 Apollonius of -

Central Library: IIT GUWAHATI
Central Library, IIT GUWAHATI BACK VOLUME LIST DEPARTMENTWISE (as on 20/04/2012) COMPUTER SCIENCE & ENGINEERING S.N. Jl. Title Vol.(Year) 1. ACM Jl.: Computer Documentation 20(1996)-26(2002) 2. ACM Jl.: Computing Surveys 30(1998)-35(2003) 3. ACM Jl.: Jl. of ACM 8(1961)-34(1987); 43(1996);45(1998)-50 (2003) 4. ACM Magazine: Communications of 39(1996)-46#3-12(2003) ACM 5. ACM Magazine: Intelligence 10(1999)-11(2000) 6. ACM Magazine: netWorker 2(1998)-6(2002) 7. ACM Magazine: Standard View 6(1998) 8. ACM Newsletters: SIGACT News 27(1996);29(1998)-31(2000) 9. ACM Newsletters: SIGAda Ada 16(1996);18(1998)-21(2001) Letters 10. ACM Newsletters: SIGAPL APL 28(1998)-31(2000) Quote Quad 11. ACM Newsletters: SIGAPP Applied 4(1996);6(1998)-8(2000) Computing Review 12. ACM Newsletters: SIGARCH 24(1996);26(1998)-28(2000) Computer Architecture News 13. ACM Newsletters: SIGART Bulletin 7(1996);9(1998) 14. ACM Newsletters: SIGBIO 18(1998)-20(2000) Newsletters 15. ACM Newsletters: SIGCAS 26(1996);28(1998)-30(2000) Computers & Society 16. ACM Newsletters: SIGCHI Bulletin 28(1996);30(1998)-32(2000) 17. ACM Newsletters: SIGCOMM 26(1996);28(1998)-30(2000) Computer Communication Review 1 Central Library, IIT GUWAHATI BACK VOLUME LIST DEPARTMENTWISE (as on 20/04/2012) COMPUTER SCIENCE & ENGINEERING S.N. Jl. Title Vol.(Year) 18. ACM Newsletters: SIGCPR 17(1996);19(1998)-20(1999) Computer Personnel 19. ACM Newsletters: SIGCSE Bulletin 28(1996);30(1998)-32(2000) 20. ACM Newsletters: SIGCUE Outlook 26(1998)-27(2001) 21. -
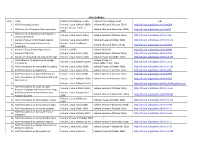
ACM JOURNALS S.No. TITLE PUBLICATION RANGE :STARTS PUBLICATION RANGE: LATEST URL 1. ACM Computing Surveys Volume 1 Issue 1
ACM JOURNALS S.No. TITLE PUBLICATION RANGE :STARTS PUBLICATION RANGE: LATEST URL 1. ACM Computing Surveys Volume 1 Issue 1 (March 1969) Volume 49 Issue 3 (October 2016) http://dl.acm.org/citation.cfm?id=J204 Volume 24 Issue 1 (Feb. 1, 2. ACM Journal of Computer Documentation Volume 26 Issue 4 (November 2002) http://dl.acm.org/citation.cfm?id=J24 2000) ACM Journal on Emerging Technologies in 3. Volume 1 Issue 1 (April 2005) Volume 13 Issue 2 (October 2016) http://dl.acm.org/citation.cfm?id=J967 Computing Systems 4. Journal of Data and Information Quality Volume 1 Issue 1 (June 2009) Volume 8 Issue 1 (October 2016) http://dl.acm.org/citation.cfm?id=J1191 Journal on Educational Resources in Volume 1 Issue 1es (March 5. Volume 16 Issue 2 (March 2016) http://dl.acm.org/citation.cfm?id=J814 Computing 2001) 6. Journal of Experimental Algorithmics Volume 1 (1996) Volume 21 (2016) http://dl.acm.org/citation.cfm?id=J430 7. Journal of the ACM Volume 1 Issue 1 (Jan. 1954) Volume 63 Issue 4 (October 2016) http://dl.acm.org/citation.cfm?id=J401 8. Journal on Computing and Cultural Heritage Volume 1 Issue 1 (June 2008) Volume 9 Issue 3 (October 2016) http://dl.acm.org/citation.cfm?id=J1157 ACM Letters on Programming Languages Volume 2 Issue 1-4 9. Volume 1 Issue 1 (March 1992) http://dl.acm.org/citation.cfm?id=J513 and Systems (March–Dec. 1993) 10. ACM Transactions on Accessible Computing Volume 1 Issue 1 (May 2008) Volume 9 Issue 1 (October 2016) http://dl.acm.org/citation.cfm?id=J1156 11. -

Robert Grossman Curriculum Vita
Robert Grossman Curriculum Vita Summary Robert Grossman is a faculty member at the University of Chicago, where he is the Director of Informatics at the Institute for Genomics and Systems Biology, a Senior Fellow at the Computation Institute, and a Professor of Medicine in the Section of Genetic Medicine. His research group focuses on bioinformatics, data mining, cloud computing, data intensive computing, and related areas. He is also the Chief Research Informatics Officer of the Biological Sciences Division. From 1998 to 2010, he was the Director of the National Center for Data Mining at the University of Illinois at Chicago (UIC). From 1984 to 1988 he was a faculty member at the University of California at Berkeley. He received a Ph.D. from Princeton in 1985 and a B.A. from Harvard in 1980. He is also the Founder and a Partner of Open Data Group. Open Data provides management consulting and outsourced analytic services for businesses and organizations. At Open Data, he has led the development of analytic systems that are used by millions of people daily all over the world. He has published over 150 papers in refereed journals and proceedings and edited seven books on data intensive computing, bioinformatics, cloud computing, data mining, high performance computing and networking, and Internet technologies. Prior to founding the Open Data Group, he founded Magnify, Inc. in 1996. Magnify provides data mining solutions to the insurance industry. Grossman was Magnify’s CEO until 2001 and its Chairman until it was sold to ChoicePoint in 2005. ChoicePoint was acquired by LexisNexis in 2008. -

FCRC 2011 June 4 - 11, San Jose, CA TIMELINE SCHEDULE
FCRC 2011 June 4 - 11, San Jose, CA TIMELINE SCHEDULE Sponsored by Corporate Support Provided by Gold Silver CONFERENCE/WORKSHOP/EVENT ACRONYMS & DATES Dates Full Name Dates Full Name 3DAPAS 8 A Workshop on Dynamic Distrib. Data-Intensive Applications, Programming Abstractions, & Systs (HPDC) IWQoS 6--7 Int. Workshop on Quality of Service (ACM SIGMETRICS and IEEE Communications Society) A4MMC 4 Applications fo Multi and Many Core Processors: Analysis, Implementation, and Performance (ISCA) LSAP 8 P Workshop on Large-Scale System and Application Performance (HPDC) AdAuct 5 Ad Auction Workshop (EC) MAMA 8 Workshop on Mathematical Performance Modeling and Analysis (METRICS) AMAS-BT 4 P Workship on Architectural and Microarchitectural Support for Binary Translation (ISCA) METRICS 7--11 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems BMD 5 Workshop on Bayesian Mechanism Design (EC) MoBS 5 A Workshop on Modeling, Benchmarking, and Simulation (ISCA) CARD 5 P Workshop on Computer Architecture Research Directions (ISCA) MRA 8 Int. Workshop on MapReduce and its Applications (HPDC) CBP 4 P JILP Workshop on Computer Architecture Competitions: Championship Branch Prediction (ISCA) MSPC 5 Memory Systems Performance and Correctness (PLDI) Complex 8--10 IEEE Conference on Computational Complexity (IEEE TCMFC) NDCA 5 A New Directions in Computer Architecture (ISCA) CRA-W 4--5 CRA-W Career Mentoring Workshop NetEcon 6 Workshop on the Economics of Networks, Systems, and Computation (EC) DIDC 8 P Int. Workshop on Data-Intensive Distributed Computing (HPDC) PLAS 5 Programming Languages and Analysis for Security Workshop (PLDI) EAMA 4 Workshop on Emerging Applications and Manycore Architectures (ISCA) PLDI 4--8 ACM SIGPLAN Conference on Programming Language Design and Implementation EC 5--9 ACM Conference on Electronic Commerce (ACM SIGECOM) PODC 6--8 ACM SIGACT-SIGOPT Symp. -

Automatic Complexity Analysis of Explicitly Parallel Programs
Automatic Complexity Analysis of Explicitly Parallel Programs Torsten Hoefler Grzegorz Kwasniewski ETH Zurich ETH Zurich Zurich, Switzerland Zurich, Switzerland [email protected] [email protected] ABSTRACT This implies that programmers need to expose exponen- The doubling of cores every two years requires programmers tially growing parallelism to exploit the full potential of the to expose maximum parallelism. Applications that are de- architecture. Parallel programming is generally hard and veloped on today's machines will often be required to run on practical implementations may not always expose enough many more cores. Thus, it is necessary to understand how parallelism to be considered future-proof. This is exagger- much parallelism codes can expose. The work and depth ated by continuous application development and the fact model provides a convenient mental framework to assess the that applications are developed on systems with significantly required work and the maximum parallelism of algorithms lower core counts than their production environment. Thus, and their parallel efficiency. We propose an automatic anal- it is increasingly important that programmers understand ysis to extract work and depth from a source-code. We do bounds on the scalability of their implementation. this by statically counting the number of loop iterations de- Parallel codes are manifold and numerous programming pending on the set of input parameters. The resulting ex- frameworks exist to implement parallel versions of sequen- pression can be used to assess work and depth with regards tial codes. We define the class of explicitly parallel codes as to the program inputs. Our method supports the large class applications that statically divide their workload into sev- of practically relevant loops with affine update functions and eral pieces which are processed in parallel. -

American Jeurnal of Computational Linguistics
American Jeurnal of Computational Linguistics NEWSLETTER OF THE ASSOCIATION FOR COMPUTATIONPEC LINGUI StICS VOLUME 14 - NUMBER 1 FEBRUARY1977 NEW MANAGING EDITOR Donald E Walker has accepted the responsibilities of Managing Editor of AJCL along with those of Secretary-Treasurer of the Association He needs time to obtain and sort the records and stocks formerly held by the Center for Applied Linguistics, but will soon be ready to provide prompt service to members and institutional subscribers EDITORIAL BOARD CHANGES Five new members have joined the Board Jonathan Allen, Gary G Hendrux, C Raymond Perreault, Jane Robinson, and William C Rounds See frames 3-5 of this fiche FORMAT SHIFT To conserve production money, AJCL now uses blank frames following the text of some contributions for news and other material formerly collected in The Finite String AMERICAN JOURNAL OF COMPUTATIONAL LINGUISTICS is published by the Association for Computational Linguistics EDITOR David G Hays, Professor of Linguistics and of Computer Science, State University of New York, Buffalo EDITORIAL ASSISTANT William Benzon EDITORIAL ADDRESS 5048 ~akeShore Rbad, Hamburg, New York 14075 TECHNICAL ADVISOR Martin Kay, Xerox Palo Alto Research Center MANAGING EDITOR Donald E Walker PRODUCTION AND SUBSCRIPTION ADDRESS. Artificial Intelligence Center, Stanford Research Institute, Menlo Park, California 94025 Assoclatlon for Computational Llngulstlcs CONTENTS EDITORIAL BOARD: Three-year terms inaugurated EULOGY af A Ljudskanov by G Rondeau LETTERS concerning Igor Mel'chuk IFIF -

Subscriber Renewal Guide
Advancing Computing as a Science & Profession Subscriber Renewal Guide www.acm.org Dear Subscriber: Your subscription(s) will expire shortly. We urge you to renew quickly to assure continuous service. Please contact us if you have any questions. Adding Service(s): Just list the service(s) you wish to add on the front of your invoice. Be sure to include the appropriate rate(s). Indicate your new Total Amount. ACM offers Expedited Air Service—a partial air service for residents outside of North America. Publications will be delivered within 7 to 14 days. For complete publication information: www.acm.org/publications For non-member subscription information: www.acm.org/publications/alacarte How to Contact ACM Hours: 8:30a.m. to 4:30p.m. Mail: ACM Member Services Dept. (US Eastern Time) General Post Office Phone: 1-800-342-6626 (US & Canada) P.O. Box 30777 +1-212-626-0500 (Global) New York, NY 10087-0777 USA Fax: +1-212-944-1318 Email: [email protected] www.acm.org 07ACM124356 Applications and Research Based Publications Individual Pricing * Institutional Pricing † Magazines and Journals: Issues Per Print Online Print+Online Print Online Print+Online Air Year Collective Intelligence 12 Price ** GOLD OPEN ACCESS ** ** GOLD OPEN ACCESS ** Offer Code Communications of the ACM 12 Price $319 $255 $383 $1,266 $1,014 $1,521 $76 Offer Code 101 201 301 101L 201L 301L Computing Reviews 12 Price $340 $272 n/a $1,036 n/a n/a $50 Offer Code 104 204 104L Computing Surveys 4 Price $305 $244 $366 $887 $711 $1,070 $43 Offer Code 103 203 303 103L 203L 303L Digital -

ACM Student Membership Application and Order Form
student membership application and order form INSTRUCTIONS Name Please print clearly Member Number Carefully complete this PDF applica - tion and return with payment by mail Address or fax to ACM. You must be a full-time student to qualify for student rates. City State/Province Postal code/Zip Ë CONTACT ACM Country Please do not release my postal address to third parties Area code & Daytime phone Email address Ë Yes, please send me ACM Announcements via email Ë No, please do not send me ACM Announcements via email phone: 1-800-342-6626 (US & Canada) +1-212-626-0500 MEMBERSHIP OPTIONS & ADD ONS (Global) MEMBERSHIP OPTIONS: hours: 8:30am - 4:30pm US Eastern Time Ë Student Membership: $19 (USD) fax: +1-212-944-1318 Ë Student Membership PLUS Digital Library: $42 (USD) [email protected] email: Ë Student Membership PLUS Print CACM Magazine: $42 (USD) mail: ACM, Member Services Ë General Post Office Student Membership w/Digital Library PLUS Print CACM Magazine: $62 (USD) P.O. Box 30777 MEMBERSHIP ADD ONS: NY, NY 10087-0777, USA Ë ACM Books Subscription: $10 (USD) For immediate processing, Ë FAX this application to Additional Print Publications and/or Special Interest Groups +1-212-944-1318. PUBLICATIONS Please check one WHAT’S NEW Check the appropriate box and calculate Issues amount due on reverse. per year Code Member Rate Air Rate* ACM Learning Webinars keep you at the • ACM Inroads 4 178 $41 Ë $69 Ë Ë Ë cutting edge of the latest technical and tech - • Communications of the ACM 12 101 $50 $69 • Computers in Entertainment (online only) 4 247 $48 Ë N/A nological developments. -

Acm Digital Library 매뉴얼
ACM DIGITAL LIBRARY 매뉴얼 신원데이터넷 [email protected] Confidential 1 ⓒ 2020 Shinwon Datanet Co., Ltd TABLE OF CONTENTS 1. 출판사 소개 2. 수록내용 3. The ACM Digital Library 4. The Guide to Computing Literature Confidential 2 ⓒ 2020 Shinwon Datanet Co., Ltd 1. 출판사 소개 Association for Computing Machinery (ACM) - 1947년 설립된 미국컴퓨터협회 ACM(http://www.acm.org)은 컴퓨터 및 IT 관련 모든 분야에 대한 최신 정보를 제공하는 협회로, 현재 전 세계 190 여 개 국 150,000 여 명 이상의 회원 보유 - ACM 회원들은 단순히 기술보고서나 논문을 게재하는 활동 이외에도, 연구 시 발생 되었던 문제들과 해결 방법, 그리고 수록된 기술 보고서나 논문에 대한 Review를 제시함으로써 컴퓨터 관련 분야의 가장 권위 있는 Community를 형성하고 있음 Confidential 3 ⓒ 2020 Shinwon Datanet Co., Ltd 1. 출판사 소개 SIG(Special Interest Groups) • ACM 내 소 주제분야 관련 분과회 • 전세계 170개의 컨퍼런스, 워크샵, 심포지엄을 주관 • 컴퓨터 IT 관련 분야의 37개 분과에서 관련 연구 및 정보 교환 SIGACCESS Accessibility and Computing SIGKDD Knowledge Discovery in Data SIGACT Algorithms & Computation Theory SIGLOG Logic and Computation SIGAI Artificial Intelligence SIGMETRICS Measurement and Evaluation SIGAPP Applied Computing SIGMICRO Microarchitecture SIGARCH Computer Architecture SIGMIS Management Information Systems SIGAda Ada Programming Language SIGMM Multimedia Systems SIGBED Embedded Systems SIGMOBILE Mobility of Systems, Users, Data & Computing SIGBio Bioinformatics, Computational Biology SIGMOD Management of Data SIGCAS Computers and Society SIGOPS Operating Systems SIGCHI Computer SIGPLAN Programming Languages SIGCOMM Data Communication SIGSAC Security, Audit and Control SIGCSE Computer Science Education SIGSAM Symbolic & Algebraic Manipulation SIGDA Design Automation SIGSIM Simulation SIGDOC Design of Communication SIGSOFT Software Engineering SIGEVO Genetic and Evolutionary Computation SIGSPATIAL Spatial Information SIGGRAPH Computer Graphics SIGUCCS University & College Computing Services SIGHPC High Performance Computing SIGWEB Hypertext, Hypermedia and Web SIGIR Information Retrieval SIGecom Electronic Commerce SIGITE Information Technology Education Confidential ⓒ 2020 Shinwon Datanet Co., Ltd 4 2. -

Human Centered Computing New Degree
HCC PhD New Degree Proposal April, 17 2015 GC1 Board of Governors, State University System of Florida Request to Offer a New Degree Program (Please do not revise this proposal format without prior approval from Board staff) University of Florida Fall 2016 University Submitting Proposal Proposed Implementation Term CISE College of Engineering Name of College(s) or School(s) Name of Department(s)/ Division(s) Doctor of Philosophy Human-Centered Computing Academic Specialty or Field Complete Name of Degree 11.0104 Proposed CIP Code The submission of this proposal constitutes a commitment by the university that, if the proposal is approved, the necessary financial resources and the criteria for establishing new programs have been met prior to the initiation of the program. Date Approved by the University Board of President Date Trustees Signature of Chair, Board of Date Vice President for Academic Date Trustees Affairs Provide headcount (HC) and full-time equivalent (FTE) student estimates of majors for Years 1 through 5. HC and FTE estimates should be identical to those in Table 1 in Appendix A. Indicate the program costs for the first and the fifth years of implementation as shown in the appropriate columns in Table 2 in Appendix A. Calculate an Educational and General (E&G) cost per FTE for Years 1 and 5 (Total E&G divided by FTE). Projected Implementatio Projected Program Costs Enrollment n Timeframe (From Table 2) (From Table 1) E&G Contract E&G Auxiliary Total HC FTE Cost per & Grants Funds Funds Cost FTE Funds Year 1 12 8.4 55,740 468,215 0 0 468,215 Year 2 20 14 Year 3 30 21 Year 4 40 28 Year 5 50 35 15,057 526,981 0 0 526,981 Note: This outline and the questions pertaining to each section must be reproduced within the body of the proposal to ensure that all sections have been satisfactorily addressed.