DOCSLIB.ORG

Kinematics of Ductile Shear Zones with Deformable Or Mobile Walls

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Kinematics of Ductile Shear Zones with Deformable Or Mobile Walls J. Earth Syst. Sci. (2019) 128 218 Ó Indian Academy of Sciences https://doi.org/10.1007/s12040-019-1238-y (0123456789().,-volV)(0123456789().,-volV) Kinematics of ductile shear zones with deformable or mobile walls 1, 2 KIERAN FMULCHRONE * and SOUMYAJIT MUKHERJEE 1 Department of Applied Mathematics, School of Mathematical Sciences, University College, Cork, Ireland. 2 Department of Earth Sciences, Indian Institute of Technology Bombay, Powai, Mumbai, Maharashtra 400 076, India. *Corresponding author. e-mail: [email protected] MS received 22 May 2018; revised 21 February 2019; accepted 16 May 2019 Shear zones are important phenomena in the Earth’s middle and lower crust and are of great interest to structural geologists. Models involving rigid boundaries moving parallel to themselves are extended here to include the case where (i) walls are deformable and (ii) mobile rigid walls approach each other. These models are combined with Couette and Poiseuille flow to define a broad range of kinematic possibilities. Deformable wall models lead to smooth transitions from deformed to undeformed materials as well as with the zone transitions to gentler and more spread out deformation. Mobile walls, on the other hand, lead to shear zones where shear sense can change along a shear zone boundary. Keywords. Shear zone kinematics; rheology; structural geology; deformation mechanism; Couette flow; fluid mechanics. 1. Introduction context); (iv) Poiseuille flow: the boundaries of the shear zone remain static and an along zone pres- Ductile shear zones at different scales of observa- sure difference causes flow along the shear zone tion are intensely studied by structural geologists (figure 1d; Beaumont et al. 2001); and (v) com- because, in addition to theoretical reasons (Fossen bined simple shear and Poiseuille flow: the and Cavalcante 2017), these zones define major boundaries shear past each other along with a plate boundaries and are the loci of seismicity pressure gradient-induced fluid flow inside the zone (Regenauer-Lieb and Yuen 2003). Taking the (figure 1e; Mukherjee and Koyi 2010). Recently, simplest case of a shear zone with parallel rigid these different ductile shear mechanisms have been boundaries, several kinds of ductile shear have discussed and debated vigorously in the context of been recognised: (i) simple shear/Couette flow: extrusion of portions of large, hot orogens, such as where one or both the boundaries move parallel to the Greater Himalayan Crystallines (Appendix of themselves (figure 1a; Ramsay 1980); (ii) pure Mukherjee 2013a). At a much smaller scale, flow of shear/cream-cake model: the boundaries move partially molten material through brittle planes perpendicular to themselves (figure 1b; Mukherjee can follow a Poiseuille flow mechanism during the submitted), (iii) general shear/sub-simple shear: ductile shear process. Assuming an incompressible the boundaries move in a way that have both Newtonian rheology for material inside the shear simple- and pure shear components (figure 1c; zone, velocity profiles for simple shear through a Vannay and Grasemann (2001) in a tectonic horizontal shear zone are linear, and for all other 218 Page 2 of 11 J. Earth Syst. Sci. (2019) 128 218 Figure 1. Ductile shear kinematics. Parallel boundary cases: (a) Simple shear; (b) Pure shear; (c) General shear, (d) Poiseuille flow of a Newtonian fluid; (e) Combined simple shear and Poiseuille flow; (f) Poiseuille flow of a non-Newtonian fluid. Non- parallel boundary cases: (g) Slipping boundary; (h) Simple shear with tapering boundaries; (i) Jeffery Hamel flow of Newtonian fluid. (j) Simple shear within a circular zone. Refer to section 1: Introduction. ductile shear types referred above they look The possibility of shear zones with deformable or parabolic. For non-Newtonian rheology, Couette mobile boundaries has been recognised for some flow profile is non-specific (Hobbs 1972), and for a time (Bailey et al. 2004 and references therein) but purely Poiseuille flow bell-shaped (figure 1f; Tur- their kinematic details are not well known. For cotte and Schubert 2014). example, Lisle (2014) analysed the kinematics of Besides, these common ductile shear patterns, ductile deformation assuming the rigid boundaries. Mandal et al. (2002) analogue modelled flow kine- Flattening/pure shear of a zone with deformable matics for tapering ductile shear zones with rigid walls was analysed only by Mandal et al. (2001). walls (figure 1h). Mukherjee et al. (2012) mechan- Their kinematic analysis involves a parameter that ically modelled ductile extrusion through a shear defines the competency contrast between the shear zone that converges at depth (figure 1i). Mukherjee zone rock and its wall rock. Ductile sheared mig- and Biswas (2014, 2015) analytically modelled matites can be characterised by leucosome layers simple shear flow profile through circular horizon- defining the primary shear planes near which tal shear zones (figure 1j). Mulchrone and alternate layers of leucosomes and melanosomes Mukherjee (2016) investigated the simple shear swerve defining S-fabrics (Mukherjee 2010). The with or without Poiseuille flow for slipping occurrence of leucosome layers along C-planes boundary cases (figure 1g). indicates the syntectonic/syn-shear migmatisation J. Earth Syst. Sci. (2019) 128 218 Page 3 of 11 218 (Marchildon and Brown 2003). While undergoing (Mukherjee 2013b). In phyllites, the ratio of migmatisation, the leucosome was in a fluid stage. viscosity between mica-poor and mica-rich layers We, therefore, interpret the common observations ranges 1–2 (Bayly 1970). Except for a single esti- that such C-planes are not perfectly planar mate of viscosity (1021–1022 Pa s) for a feldspar-rich (figure 2a, b), as an indication of internal ductile rock at high temperatures (Rybacki et al. 2002), deformation of the soft fluid layer. Lloyd et al. viscosity magnitudes of ductile deforming micas, (1992) reported the deformed shear zone margins at quartz and feldspar are largely unknown. In the the grain scale from mylonites in Scotland. Zhang ductile regime, below 8–15 km depth, there is no et al. (2012) document the deformed footwall of a guarantee that the shear zone material deforms in a shear zone from Yiwulushan (China), both having ductile manner while simultaneously the surround- similar kinematic indicators. Roy Choudhury et al. ing rocks behave rigidly. (2016) documented the deformation in the footwall Mica-rich layers defining narrow shear zones of a mylonitised shear zone (Rajasthan, India). inside a quartzofeldspathic matrix are common in It will be important not to compare the present many rock types (e.g., Mukherjee 2013b), where model with cases where the shear zone boundary the shear zone boundaries are defined by preferred deformed after the ductile deformation e.g., a alignment of micas that are recognised also as C- or brittle deformed margin in a metamorphic core primary shear planes (Passchier and Trouw 2005). complex (Davis 1983). We presently neither have viscosity magnitudes Shear zone boundaries act rigidly when the ratio nor ratios of such micas and quartzofeldspathic of viscosity between the shear zone and the sur- minerals to compare whether theoretically such rounding rocks is 10-7 (Mancktelow 2008). How- mica layers can act rigidly during the shear. A ever, inside such rigid ‘‘ÁÁÁboundaries, the softer common observation, however, is that such mica rock would produce primary shear planes parallel to layers are not always perfectly straight in meso- the boundaries of the shear zones’’ (Passchier and (figure 2a–d) and micro-scales (figure 3a–d), pos- Trouw 2005). Note that we do not mean those C- sibly indicating that mica layers acted as deform- planes to act as shear zone boundaries in this paper. able boundaries of such shear zones. A similar Such C-planes to are locally found to be warped conclusion can be drawn from ductile shear zones recognised on mega-scales using the remote sensing images (Pour and Hashim 2016). C-planes are readily recognised based on sharp termination/ swerving of S-fabrics and are clearly curving in exposures and therefore must also be curvi-planar in 3D. Note that at smaller scales step-overs (of mica fish trails denoting the mylonitic foliation/C-plane: Lister and Snoke 1984) and possibly intrafolial folded C-planes indicate ductile shear of the C- plane themselves. Thus, there is a need to extend the kinematic theory of ductile shear zones to include the case of deformable and mobile bound- aries in structural geology. Figure 2. Ductile shear zones in meso-scale, with non-planar All analogue and most numerical models of shear C-plane. Reproduced from figures 1.4, 1.5, 1.49 and 2.7, zones in structural geology and tectonics tend to respectively, of Mukherjee and Biswas (2014). Blue full arrow: consider the rigid boundaries. Curviplanar margins curved C-plane. (a, b) S-fabric defined by thicker leucosome of shear zones were implicitly presumed to be pre- and thinner and close-spaced melanosome layers C-plane traces white line. Top-to-S (top-to-right) shear. Greater deformational. Curved primary ductile shear Himalayan Crystallines, Sutlej river section, Himachal Pra- planes in meso-scales (Coward 1976) and in hand desh state, India. (c) A delta structure of quartz clast. Top-to- specimens (Gapais et al. 1987) are well known. S (top-to-left up) sheared. Bhagirathi section of Greater Hyperbolic- and linear flow paths for pure and Himalayan Crystallines, India. (d) A train of intrafolial fold simple shear zones (Schlichting 1960) have also (Mukherjee and Biswas 2015) bound by C-planes. Top-to-NE down (top-to-left down) sheared. Near Karcham, Himachal been well established. However, the velocity pro- Pradesh, Sutlej river section, Greater Himalayan Crystallines, les for shear zones with deformable boundaries India. have not been explored. 218 Page 4 of 11 J. Earth Syst. Sci. (2019) 128 218 Figure 3. Ductile shear zone within mylonitized gneiss in micro-scale, with non-planar C-plane, all photomicrographs lengths are 0.24 mm.
Load more

Recommended publications
  • Chapter 8 Large Strains
    Chapter 8 Large Strains Introduction Most geological deformation, whether distorted fossils or fold and thrust belt shortening, accrues over a long period of time and can no longer be analyzed with the assumptions of infinitesimal strain. Fortunately, these large, or finite strains have the same starting point that infinitesimal strain does: the deformation and dis- placement gradient tensors. However, we must clearly distinguish between gradi- ents in position or displacement with respect to the initial (material) or to the final (spatial) state and several assumptions from the last Chapter — small angles, addi- tion of successive phases or steps in the deformation — no longer hold. Finite strain can get complicated very quickly with many different tensors to worry about. Most of our emphasis here will be on the practical measurement of finite strain rather than the details of the theory but we do have to review a few basic concepts first, so that we can appreciate the differences between finite and infinitesimal strain. Some of these differences have a profound impact on how we analyze de- formation. CHAPTER 8 FINITE STRAIN Comparison to Infinitesimal Strain A Plethora of Finite Strain Tensors There are lots of finite strain tensors and they come in pairs: one referenced to the initial state and the other referenced to the final state. The derivation of these tensors is usually based on Figure 7.3 and is tedious but straightforward; we will skip the derivation here but you can see it in Allmendinger et al. (2012) or any good continuum mechanics text. The first tensor is the Lagrangian strain tensor: 1 ⎡ ∂ui ∂u j ∂uk ∂uk ⎤ 1 " Lij = ⎢ + + ⎥ = ⎣⎡Eij + E ji + EkiEkj ⎦⎤ (8.1) 2 ⎣∂ X j ∂ Xi ∂ Xi ∂ X j ⎦ 2 where Eij is the displacement gradient tensor from the last Chapter.
    [Show full text]
  • Gy403 Structural Geology Kinematic Analysis Kinematics
    GY403 STRUCTURAL GEOLOGY KINEMATIC ANALYSIS KINEMATICS • Translation- described by a vector quantity • Rotation- described by: • Axis of rotation point • Magnitude of rotation (degrees) • Sense of rotation (reference frame; clockwise or anticlockwise) • Dilation- volume change • Loss of volume = negative dilation • Increase of volume = positive dilation • Distortion- change in original shape RIGID VS. NON-RIGID BODY DEFORMATION • Rigid Body Deformation • Translation: fault slip • Rotation: rotational fault • Non-rigid Body Deformation • Dilation: burial of sediment/rock • Distortion: ductile deformation (permanent shape change) TRANSLATION EXAMPLES • Slip along a planar fault • 360 meters left lateral slip • 50 meters normal dip slip • Classification: normal left-lateral slip fault 30 Net Slip Vector X(S) 40 70 N 50m dip slip X(N) 360m strike slip 30 40 0 100m ROTATIONAL FAULT • Fault slip is described by an axis of rotation • Rotation is anticlockwise as viewed from the south fault block • Amount of rotation is 50 degrees Axis W E 50 FAULT SEPARATION VS. SLIP • Fault separation: the apparent slip as viewed on a planar outcrop. • Fault slip: must be measured with net slip vector using a linear feature offset by the fault. 70 40 150m D U 40 STRAIN ELLIPSOID X • A three-dimensional ellipsoid that describes the magnitude of dilational and distortional strain. • Assume a perfect sphere before deformation. • Three mutually perpendicular axes X, Y, and Z. • X is maximum stretch (S ) and Z is minimum stretch (S ). X Z Y Z • There are unique directions
    [Show full text]
  • Ductile Deformation - Concepts of Finite Strain
    327 Ductile deformation - Concepts of finite strain Deformation includes any process that results in a change in shape, size or location of a body. A solid body subjected to external forces tends to move or change its displacement. These displacements can involve four distinct component patterns: - 1) A body is forced to change its position; it undergoes translation. - 2) A body is forced to change its orientation; it undergoes rotation. - 3) A body is forced to change size; it undergoes dilation. - 4) A body is forced to change shape; it undergoes distortion. These movement components are often described in terms of slip or flow. The distinction is scale- dependent, slip describing movement on a discrete plane, whereas flow is a penetrative movement that involves the whole of the rock. The four basic movements may be combined. - During rigid body deformation, rocks are translated and/or rotated but the original size and shape are preserved. - If instead of moving, the body absorbs some or all the forces, it becomes stressed. The forces then cause particle displacement within the body so that the body changes its shape and/or size; it becomes deformed. Deformation describes the complete transformation from the initial to the final geometry and location of a body. Deformation produces discontinuities in brittle rocks. In ductile rocks, deformation is macroscopically continuous, distributed within the mass of the rock. Instead, brittle deformation essentially involves relative movements between undeformed (but displaced) blocks. Finite strain jpb, 2019 328 Strain describes the non-rigid body deformation, i.e. the amount of movement caused by stresses between parts of a body.
    [Show full text]
  • Geometry and Kinematics of Bivergent Extension in the Southern Cycladic Archipelago: Constraining an Extensional Hinge Zone on S
    RESEARCH ARTICLE Geometry and Kinematics of Bivergent Extension in 10.1029/2020TC006641 the Southern Cycladic Archipelago: Constraining an Key Points: Extensional Hinge Zone on Sikinos Island, Aegean Sea, • New and novel (re)interpretation of extension-related structures in Greece Cycladic Blueschist Unit • Extensional structures resulted from Uwe Ring1 and Johannes Glodny2 high degree of pure-shear flattening during general-shear deformation 1Department of Geological Sciences, Stockholm University, Stockholm, Sweden, 2GFZ German Research Centre for • Structures are interpreted to reflect Geosciences, Potsdam, Germany an extensional hinge zone in southern Cyclades Abstract We report the results of a field study on Sikinos Island in the Aegean extensional province Supporting Information: of Greece and propose a hinge zone controlling incipient bivergent extension in the southern Cyclades. Supporting Information may be found A first deformation event led to top-S thrusting of the Cycladic Blueschist Unit (CBU) onto the Cycladic in the online version of this article. basement in the Oligocene. The mean kinematic vorticity number (Wm) during this event is between 0.56 and 0.63 in the CBU, and 0.72 to 0.84 in the basement, indicating general-shear deformation with about Correspondence to: equal components of pure and simple shear. The strain geometry was close to plane strain. Subsequent U. Ring, [email protected] lower-greenschist-facies extensional shearing was also by general-shear deformation; however, the pure- shear component was distinctly greater (Wm = 0.3–0.41). The degree of subvertical pure-shear flattening Citation: increases structurally upward and explains alternating top-N and top-S shear senses over large parts of Ring, U., & Glodny, J.
    [Show full text]
  • 2 Review of Stress, Linear Strain and Elastic Stress- Strain Relations
    2 Review of Stress, Linear Strain and Elastic Stress- Strain Relations 2.1 Introduction In metal forming and machining processes, the work piece is subjected to external forces in order to achieve a certain desired shape. Under the action of these forces, the work piece undergoes displacements and deformation and develops internal forces. A measure of deformation is defined as strain. The intensity of internal forces is called as stress. The displacements, strains and stresses in a deformable body are interlinked. Additionally, they all depend on the geometry and material of the work piece, external forces and supports. Therefore, to estimate the external forces required for achieving the desired shape, one needs to determine the displacements, strains and stresses in the work piece. This involves solving the following set of governing equations : (i) strain-displacement relations, (ii) stress- strain relations and (iii) equations of motion. In this chapter, we develop the governing equations for the case of small deformation of linearly elastic materials. While developing these equations, we disregard the molecular structure of the material and assume the body to be a continuum. This enables us to define the displacements, strains and stresses at every point of the body. We begin our discussion on governing equations with the concept of stress at a point. Then, we carry out the analysis of stress at a point to develop the ideas of stress invariants, principal stresses, maximum shear stress, octahedral stresses and the hydrostatic and deviatoric parts of stress. These ideas will be used in the next chapter to develop the theory of plasticity.
    [Show full text]
  • Download Download
    e-ISSN 2580 - 0752 BULLETIN OF GEOLOGY Fakultas Ilmu dan Teknologi Kebumian (FITB) Institut Teknologi Bandung (ITB) STRUCTURAL CONTROL RELATED WITH MEDIUM-TO-VERY HIGH Au GRADE AT PIT B EAST AND B WEST, TUJUH BUKIT MINE, EAST JAVA ILHAM AJI DERMAWAN1, ANDRI SLAMET SUBANDRIO1, ALFEND RUDYAWAN1, ARYA DWI SANJAYA2, RAMA MAHARIEF2, KRISMA ANDITYA2, RIZFAN HASNUR2, M. SATYA MUTTAQIEN2, CICIH LARASATI WIDYA FITRI2, ANDI PAHLEVI2, DEDY DAULAY2, AGUS PURWANTO2, ADI ADRIANSYAH SJOEKRI2 1. Program Studi Teknik Geologi, Fakultas Ilmu dan Teknologi Kebumian, Institut Teknologi Bandung (ITB), Jl. Ganesha No.10, Bandung, Jawa Barat, Indonesia. Email: [email protected] 2. PT Bumi Suksesindo, Desa Sumberagung, Kecamatan Pesanggaran, Kabupaten Banyuwangi, Provinsi Jawa Timur, Indonesia. Sari – Tujuh Bukit secara umum disusun oleh batuan vulkanik dan vulkaniklastik Formasi Batuampar berumur Oligosen Akhir sampai Miosen Tengah. Setelah terjadi aktivitas tektonomagmatisme pada Pliosen, satuan tersebut teralterasi dan menjadi host rock bagi mineralisasi ekonomis yang juga terbentuk pada Pliosen. Daerah penelitian berada di tambang terbuka Pit B East dan B West. Kavling yang mencakup kedua pit tersebut memiliki luas ± 700 x 500 m2, terletak pada koordinat ± 9045100 – 9045600 mU dan ± 174400 – 175100 mT sistem proyeksi koordinat UTM WGS 1984 zona 50S. Penelitian ini membahas tentang kontrol struktur yang berperan dalam pembentukan karakteristik alterasi dan mineralisasi Au sistem epitermal sulfidasi tinggi yang berkembang di Pit B East dan B West, tambang Tujuh Bukit. Struktur geologi yang dominan berkembang berupa sistem sesar mendatar berumur Pliosen, berarah relatif NW-SE dan N-S, dengan arah tegasan utama NNW-SSE mengikuti model pure shear. Terdapat pula sesar normal berarah relatif NW-SE dan sesar naik berarah relatif ENE-WSW.
    [Show full text]
  • Formation of Melange in Afore/And Basin Overthrust Setting: Example from the Taconic Orogen
    Printed in U.S.A. Geological Society of America Special Paper 198 1984 Formation of melange in afore/and basin overthrust setting: Example from the Taconic Orogen F. W. Vollmer* William Bosworth* Department of Geological Sciences State University of New York at Albany Albany, New York 12222 ABSTRACT The Taconic melanges of eastern New York developed through the progressive deformation of a synorogenic flysch sequence deposited within a N-S elongate foreland basin. This basin formed in front of the Taconic Allochthon as it was emplaced onto the North American continental shelf during the medial Ordovician Taconic Orogeny. The flysch was derived from, and was subsequently overridden by the allochthon, resulting in the formation of belts of tectonic melange. An east to west decrease in deformation intensity allows interpretation of the structural history of the melange and study of the flysch-melange transition. The formation of the melange involved: isoclinal folding, boudinage and disruption of graywacke-shale sequences due to ductility contrasts; sub­ aqueous slumping and deposition of olistoliths which were subsequently tectonized and incorporated into the melange; and imbrication of the overthrust and underthrust sedi­ mentary sections into the melange. The characteristic microstructure of the melange is a phacoidal conjugate-shear cleavage, which is intimately associated with high strains and bedding disruption. Rootless isoclines within the melange have apparently been rotated into an east-west shear direction, consistent with fault, fold, and cleavage orientations within the flysch. The melange zones are best modeled as zones of high shear strain developed during the emplacement of the Taconic Allochthon. Total displacement across these melange zones is estimated to be in excess of 60 kilometers.
    [Show full text]
  • Study of Small-Scale Structures and Their Significance in Unravelling the Accretionary Character of Singhbhum Shear Zone, Jharkhand, India
    J. Earth Syst. Sci. (2020) 129:227 Ó Indian Academy of Sciences https://doi.org/10.1007/s12040-020-01496-9 (0123456789().,-volV)(0123456789().,-volV) Study of small-scale structures and their significance in unravelling the accretionary character of Singhbhum shear zone, Jharkhand, India 1 2, ABHINABA ROY and ABDUL MATIN * 1Formerly Geological Survey of India, New Delhi, India. 2Formerly Department of Geology, University of Calcutta, Kolkata, India. *Corresponding author. e-mail: [email protected] MS received 1 April 2020; revised 22 July 2020; accepted 29 August 2020 Localized strain within tabular ductile shear zones is developed from micro- to meso- to even large scales to form complex structures. They grow in width and length through linkage of segments with progressive accumulation of strain and displacement, and Bnally produce shear zone networks characterized by anastomosing patterns. Singhbhum shear zone (SSZ) represents a large composite zone characterized by a collage of different dismembered lithotectonic segments, with heterogeneous structural features, within a matrix typical of a shear zone. Structural features indicate that the material properties of protoliths have a great role in controlling the mechanics of deformation. Meso- and micro-scale structural studies of the east-central part of the SSZ reveal ‘tectonic complex like’ (? deeper level equivalent of melange type complex) assemblage of dismembered lithoteconic units. Shear-induced foliations, S, C and C0, were developed while the main mylonitic foliation is represented by C-plane. Apart from that, shear lenses are exceptionally well developed in both meso- and micro-scale in most of the units, particularly in schistose rocks. They were formed from different processes during progressive simple shear, which includes (1) anastomosing C-planes, (2) intersection between C- and C0-planes, (3) disruption of stretched out longer limbs of asymmetric folds, and (4) cleavage duplex.
    [Show full text]
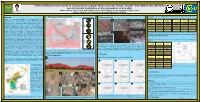
  • Field and Microstructure Study of Transpressive Jogdadi Shear Zone
    Field and Microstructure study of Transpressive Jogdadi shear zone near Ambaji, Aravalli- Delhi Mobile Belt, NW India and its tectonic implication on the exhumation of granulite Sudheer Kumar Tiwari, Tapas Kumar Biswal ([email protected], [email protected]) Indian Institute of Technology Bombay, Mumbai- 400076 Table1: Mean kinematic vorticity (WM) and percentage(%) of Pure shear for (A) Jogdadi and Surela Abstract 2. Geological map of study area 4. Microstructures shear zone N Aravalli- Delhi mobile belt is situated in the nortwestern part of Indian (A) NW SE (A) (B) shield. It comprises tectono- magmatic histories fromfrom Archean to W E Percentage (%) of Percentage (%) of A B C Sample No. Range of WM Sample No. Range of WM neoproterozoic age. It possesses three tectono- magmatic metamorphic Pure shear Pure shear C2 belts namely Bhilwara Supergroup (3000 Ma), Aravalli Supergorup (1800 Ma) S N A5 0.48- 0.53 65- 70 SA2 0.71- 0.80 42- 50 and Delhi Supergroup (1100 -750Ma). The Delhi Supergroup is divided in two (B) parts North Delhi and South Delhi; North Delhi (1100 Ma to 850 Ma) is older W E A21 0.47- 0.57 63- 71 MYL 0.73- 0.80 42- 49 than South Delhi (850 Ma to 750 Ma). The study area falls in the South Delhi JSZ A29 0.70- 0.73 48- 52 SC2 0.76- 0.82 40- 47 terrane; BKSK granulites are the major unit in this terrane. BKSK granulites S comprise gabbro- norite-basic granulite, pelitic granulite, calcareous granulite N A34 0.58- 0.61 59- 62 SE5 0.76- 0.79 44- 47 and occur within the surrounding of low grade rocks as meta- rhyolite, (C) quartzite, mica schist and amphibolites.
    [Show full text]
  • Principal Stresses
    Chapter 4 Principal Stresses Anisotropic stress causes tectonic deformations. Tectonic stress is defined in an early part of this chapter, and natural examples of tectonic stresses are also presented. 4.1 Principal stresses and principal stress axes Because of symmetry (Eq. (3.32)), the stress tensor r has real eigenvalues and mutually perpendicu- lar eigenvectors. The eigenvalues are called the principal stresses of the stress. The principal stresses are numbered conventionally in descending order of magnitude, σ1 ≥ σ2 ≥ σ3, so that they are the maximum, intermediate and minimum principal stresses. Note that these principal stresses indicate the magnitudes of compressional stress. On the other hand, the three quantities S1 ≥ S2 ≥ S3 are the principal stresses of S, so that the quantities indicate the magnitudes of tensile stress. The orientations defined by the eigenvectors are called the principal axes of stress or simply stress axes, and the orientation corresponding to the principal stress, e.g., σ1 is called the σ1-axis (Fig. 4.1). Principal planes of stress are the planes parallel to two of the stress axes, or perpendicular to one of the stress axes. Deformation is driven by the anisotropic state of stress with a large difference of the principal stresses. Accordingly, the differential stress ΔS = S1 − S3, Δσ = σ1 − σ3 is defined to indicate the difference1. Taking the axes of the rectangular Cartesian coordinates O-123 parallel to the stress axes, a stress tensor is expressed by a diagonal matrix. Therefore, Cauchy’s stress (Eq. (3.10)) formula is ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ t1(n) σ1 00 n1 ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ t(n) = t2(n) = 0 σ2 0 n2 .
    [Show full text]
  • Rifting, Seafloor Spreading, and Extensional Tectonics
    2917-CH16.pdf 11/20/03 5:21 PM Page 382 CHAPTER SIXTEEN Rifting, Seafloor Spreading, and Extensional Tectonics 16.1 Introduction 382 16.6.2 Igneous-Rock Assemblage of Rifts 397 16.2 Cross-Sectional Structure of a Rift 385 16.6.3 Active Rift Topography 16.2.1 Normal Fault Systems 385 and Rift-Margin Uplifts 399 16.2.2 Pure-Shear versus Simple-Shear 16.7 Tectonics of Midocean Ridges 402 Models of Rifting 389 16.8 Passive Margins 405 16.2.3 Examples of Rift Structure 16.9 Causes of Rifting 408 in Cross Section 389 16.10 Closing Remarks 410 16.3 Cordilleran Metamorphic Core Complexes 390 Additional Reading 410 16.4 Formation of a Rift System 394 16.5 Controls on Rift Orientation 396 16.6 Rocks and Topographic Features of Rifts 397 16.6.1 Sedimentary-Rock Assemblages in Rifts 397 16.1 INTRODUCTION phere undergoes regional horizontal extension. A rift or rift system is a belt of continental lithosphere that Eastern Africa, when viewed from space, looks like it is currently undergoing extension, or underwent exten- has been slashed by a knife, for numerous ridges, sion in the past. During rifting, the lithosphere bounding deep, gash-like troughs, traverse the land- stretches with a component roughly perpendicular to scape from north to south (Figure 16.1a and b). This the trend of the rift; in an oblique rift, the stretching landscape comprises the East African Rift, a region direction is at an acute angle to the rift trend. where the continent of Africa is quite literally splitting Geologists distinguish between active and inactive apart—land lying on the east side of the rift moves rifts, based on the timing of the extension.
    [Show full text]
  • Quantitative Finite Strain Analysis of the Quartz Mylonites Within the Three
    ZOBODAT - www.zobodat.at Zoologisch-Botanische Datenbank/Zoological-Botanical Database Digitale Literatur/Digital Literature Zeitschrift/Journal: Austrian Journal of Earth Sciences Jahr/Year: 2018 Band/Volume: 111 Autor(en)/Author(s): Kanjanapayont Pitsanupong, Ponmanee Peekamon, Grasemann Bernhard, Klötzli Urs S., Nantasin Prayath Artikel/Article: Quantitative finite strain analysis of the quartz mylonites within the Three Pagodas shear zone, western Thailand 171-179 download https://content.sciendo.com/view/journals/ajes/ajes-overview.xml Austrian Journal of Earth Sciences Vienna 2018 Volume 111/2 171 - 179 DOI: 10.17738/ajes.2018.0011 Quantitative finite strain analysis of the quartz mylonites within the Three Pagodas shear zone, western Thailand Pitsanupong KANJANAPAYONT1)*), Peekamon PONMANEE1), Bernhard GRASEMANN2), Urs KLÖTZLI3) & Prayath NANTASIN4) 1) Basin Analysis and Structural Evolution Special Task Force for Activating Research (BASE STAR), Department of Geology, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand; 2) Department of Geodynamics and Sedimentology, University of Vienna, Althanstrasse 14, Vienna 1090, Austria; 3) Department of Lithospheric Research, University of Vienna, Althanstrasse 14, Vienna 1090, Austria; 4) Department of Earth Sciences, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand; *) Corresponding author: [email protected] KEYWORDS Finite strain; Kinematic vorticity; Sinistral; Three Pagodas shear zone; Thailand Abstract The NW–trending Three Pagodas shear zone exposes a high–grade metamorphic complex named Thabsila gneiss in the Kanchanaburi region, western Thailand. The quartz mylonites within this strike–slip zone were selected for strain analysis. 2–dimensional strain analysis indicates that the averaged strain ratio (Rs) for the lower greenschist facies increment of XZ– plane is Rs = 1.60–1.97 by using the Fry’s method.
    [Show full text]