DOCSLIB.ORG

Basic Astronomy Labs

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Basic Astronomy Labs Astronomy Laboratory Exercise 22 Solar Lab The Sun (or Sol) is the nearest star to Earth. In fact, it is about 300,000 times closer to Earth than the next nearest star, Proxima Centauri. It is the only star whose surface features are clearly visible from Earth, and so it provides a glimpse into the workings of other stars. The Sun's importance can not be overstressed, for without the Sun there would be no life on Earth. This lab explores some of the features and motions of the Sun. The "surface" of the Sun can be viewed safely by projecting it onto a screen or looking through heavy filtering (such as welder's glass #14 or a special solar filter). NEVER LOOK DIRECTLY AT THE SUN, AS PERMANENT DAMAGE TO VISION MAY OCCUR! The Solar Observing Lab, Exercise 23, provides several observing exercises involving the Sun. The Sun is not a solid object, but a huge globe of glowing plasma. The "surface" that is seen through a filtered telescope or in a solar projection is the photosphere. The photosphere is that layer of the Sun from which light seems to come. But the energy of the light originates in thermonuclear fusion reactions in the core of the Sun, where hydrogen nuclei are fused into helium. The interior of the Sun can be divided into three principal parts: the core, the radiative zone, and the convective zone. In the radiative zone, light is absorbed and reemitted by the solar material. The direction in which the light is reemitted is random, so it may take millions of years for light to leave the radiative zone. At the outer boundary of the radiative zone, however, the density of the solar material is low enough for convection to occur. Material that absorbs the light is heated, rises, transmits its heat to higher materials, and falls to be heated again. The convective zone consists of loops of rising and falling material. At the photosphere, the density is low enough that the hot, rising material radiates its heat away as light then sinks to be reheated. The Sun's rotational period is not uniform across its surface; material near the equator moves about the solar axis more rapidly than material near the poles. This is called differential rotation. The sidereal rotational period of the Sun increases from about 25 days near the equator to about 34 days near the poles. However, since Earth revolves about the Sun at about 1 degree per day in the same direction that the Sun rotates, the synodic period is longer. As viewed from Earth, material near the Sun's equator takes about 27 days to complete one rotation, while material near the solar poles takes about 3 8 days. The solar rotational period at the latitude of a sunspot may be determined by measuring the sunspot's change in solar longitude (~L) over a number of days (~T) . The Sun rotates 360° in one period. Thus, the solar rotational period (P) at the latitude of the sunspot is given by P=llT·e:] . (1) 22 - 1 Example 1: A sunspot is seen to move 24 o in 2. 0 days. What is the period of rotation for material at the same latitude as the sunspot? P= (2.0· df;;o) = 30.-d Figure 22-1 illustrates the Solar Angle Device (SAD). The SAD is designed to facilitate recording the Sun's movements in the sky. It consists of a flat surface (the recording platform) mounted with a perpendicular mast. The mast may be topped by a horizontal plate with a 'V' shaped cut-out. The 'V' points toward the mast. If the 'V' is placed far enough from the mast, its shadow can be seen from the equator at solar noon on both of the solstices without reorienting the SAD. The SAD is oriented so that the recording platform is level with the ground and the shadow of the 'V' falls on the surface. The recording platform is covered with paper so a new record of the Sun's motions can be made each year. A mark is placed directly below the point of the 'V' to indicate the location of the zenith as seen from the tip of the 'V'. Also, it is convenient to mount the SAD at exactly the same location and in the same orientation each time it is used. to zenith to Snn a recording platfonn 1 tano=-} / zenith/ IE b mark Figure 22-1: Solar Angle Device (SAD) seen edge-on. The length of the shadow cast by a vertical pole can be used to determine the Sun's position in the sky. Solar noon is the time when the Sun is on the meridian. The Sun is highest in the sky at this time and shadows are shortest. During the day, the shadow of the 'V' is seen to move across the surface of the SAD. If this shadow is marked every few minutes (and the time of each mark recorded), the solar noon time can be determined later by finding the time when the shadow was shortest. The angle (8) between the Sun and the zenith is calculated using 8 =arctan(:), (2) where a is the height of the vertical mast and b is the distance of the shadow of the 'V' from the zenith mark. 22-2 Example 2: The shadow cast by the Sun of the 'V' atop a 50. em high vertical mast is 20. em north of the zenith mark at solar noon. What is the altitude and azimuth of the Sun? The angle of the Sun from the zenith is 2 8 = arctan( 0.-cm) = 22°. 50.-cm Since this shadow is measured at solar noon and the shadow is north of the zenith mark, the azimuth of the Sun is 180° (i.e., the Sun is south of the zenith). The zenith is +90° in altitude, so the Sun must be at +68° in altitude. The Sun's position in the sky depends on the location of the observer, the time and date, and the axial tilt ofEarth. Earth's rotational axis tilts with respect to the axis of the plane of its orbit (the ecliptic) by about 23.5°. On the summer solstice, the Sun appears overhead at solar noon only for people located at 23.5°N. People north of this latitude see the Sun south of the zenith and people south of this latitude see the Sun north of the zenith. After the summer solstice, the Sun's position at solar noon appears to move southward each day. On the autumnal equinox, the Sun is overhead as viewed from the equator at solar noon. On the winter solstice at solar noon, the Sun is 23.5° south of the plane ofEarth's equator and can be seen at the zenith from 23.5°S latitude. The Sun then appears to move to the north again, passing the equator on the vernal equinox. Figure 22-2 shows the changing position of the Sun in the sky during the year. The Sun is closest to the north celestial pole on the summer solstice (Figure 22-2.a) and is farthest on the winter solstice (Figure 22-2.b ). north celestial pole to zenith Figure 22-2(a): The position of Sun on the summer solstice. to ztnitl1 north cele:stial pole equator Figure 22-2(b ): The position of Sun on the winter solstice. 22- 3 The angular distance between the Sun and the zenith for a given location can be measured using the Solar Angle Device, but the latitude of the location and the axial tilt of Earth can not be measured directly. However, these values can be determined from the position of the Sun in the sky. At solar noon on the summer solstice (Figure 22-2.a), the Sun's angular distance from the zenith (8sum) is given by 8Sum = 8Lat - 8Tilt' (3) where 8Lat is the latitude angle ofthe observer's location and 8Tilt is the axial tilt ofEarth. On the winter solstice (Figure 22-2. b), the Sun's angular distance from the zenith at solar noon (8win) is given by e Win = e Lat + e Tilt · ( 4) Solving these two equations simultaneously, gives 8 = eWin + eSum (5) Lat 2 and 8 _ eWin- eSum Tilt- (6) 2 Example 3 : The angular distance of the Sun from the zenith is measured at solar noon on the winter solstice and on the summer solstice to be 58.5° and 11.5°, respectively. The Sun was south of the zenith on both occasions. Determine the latitude from which the measurements were made and the axial tilt of Earth. e = ss.so+ 11.50 = 35 oo Lat · 2 e . = 58.50-11.50 = 23 so T1lt · 2 Thus, Earth's axis tilts 23.5° and these measurements were taken from a latitude of35.0°N. The time of solar noon is different for different dates and for different locations on Earth. The daily variation in the time of solar noon is expressed by the equation of time (EOT). The equation of time gives the number of minutes that the Sun is early or late in reaching the meridian. Three factors affect the equation of time: the position ofEarth along its elliptical orbit, the axial tilt of Earth, and the location of the observer. If Earth had no axial tilt and traveled in a circular orbit, solar noon would always occur at 1200 hours for a location on a time zone line. However, Earth travels in an elliptical orbit about the Sun.
Load more

Recommended publications
  • Astrodynamics
    Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities
    [Show full text]
  • View and Print This Publication
    @ SOUTHWEST FOREST SERVICE Forest and R U. S.DEPARTMENT OF AGRICULTURE P.0. BOX 245, BERKELEY, CALIFORNIA 94701 Experime Computation of times of sunrise, sunset, and twilight in or near mountainous terrain Bill 6. Ryan Times of sunrise and sunset at specific mountain- ous locations often are important influences on for- estry operations. The change of heating of slopes and terrain at sunrise and sunset affects temperature, air density, and wind. The times of the changes in heat- ing are related to the times of reversal of slope and valley flows, surfacing of strong winds aloft, and the USDA Forest Service penetration inland of the sea breeze. The times when Research NO& PSW- 322 these meteorological reactions occur must be known 1977 if we are to predict fire behavior, smolce dispersion and trajectory, fallout patterns of airborne seeding and spraying, and prescribed burn results. ICnowledge of times of different levels of illumination, such as the beginning and ending of twilight, is necessary for scheduling operations or recreational endeavors that require natural light. The times of sunrise, sunset, and twilight at any particular location depend on such factors as latitude, longitude, time of year, elevation, and heights of the surrounding terrain. Use of the tables (such as The 1 Air Almanac1) to determine times is inconvenient Ryan, Bill C. because each table is applicable to only one location. 1977. Computation of times of sunrise, sunset, and hvilight in or near mountainous tersain. USDA Different tables are needed for each location and Forest Serv. Res. Note PSW-322, 4 p. Pacific corrections must then be made to the tables to ac- Southwest Forest and Range Exp.
    [Show full text]
  • Qiao Et Al., Sosigenes Pit Crater Age 1/51
    Qiao et al., Sosigenes pit crater age 1 2 The role of substrate characteristics in producing anomalously young crater 3 retention ages in volcanic deposits on the Moon: Morphology, topography, 4 sub-resolution roughness and mode of emplacement of the Sosigenes Lunar 5 Irregular Mare Patch (IMP) 6 7 Le QIAO1,2,*, James W. HEAD2, Long XIAO1, Lionel WILSON3, and Josef D. 8 DUFEK4 9 1Planetary Science Institute, School of Earth Sciences, China University of 10 Geosciences, Wuhan 430074, China. 11 2Department of Earth, Environmental and Planetary Sciences, Brown University, 12 Providence, RI 02912, USA. 13 3Lancaster Environment Centre, Lancaster University, Lancaster LA1 4YQ, UK. 14 4School of Earth and Atmospheric Sciences, Georgia Institute of Technology, Atlanta, 15 Georgia 30332, USA. 16 *Corresponding author E-mail: [email protected] 17 18 19 20 Key words: Lunar/Moon, Sosigenes, irregular mare patches, mare volcanism, 21 magmatic foam, lava lake, dike emplacement 22 23 24 25 1/51 Qiao et al., Sosigenes pit crater age 26 Abstract: Lunar Irregular Mare Patches (IMPs) are comprised of dozens of small, 27 distinctive and enigmatic lunar mare features. Characterized by their irregular shapes, 28 well-preserved state of relief, apparent optical immaturity and few superposed impact 29 craters, IMPs are interpreted to have been formed or modified geologically very 30 recently (<~100 Ma; Braden et al. 2014). However, their apparent relatively recent 31 formation/modification dates and emplacement mechanisms are debated. We focus in 32 detail on one of the major IMPs, Sosigenes, located in western Mare Tranquillitatis, 33 and dated by Braden et al.
    [Show full text]
  • Hunting Hours Time Zone A
    WHEN AND WHERE TO HUNT WHEN AND WHERE Hunting Hours Time Zone A. Hunting Hours for Bear, Deer, Fall Wild Turkey, Furbearers, Shown is a map of the hunting-hour time zones. Actual legal hunting hours for and Small Game bear, deer, fall wild turkey, furbearer, and small game for Time Zone A are shown One-half hour before sunrise to one-half hour after sunset (adjusted for in the table at right. Hunting hours for migratory game birds are different and are daylight saving time). For hunt dates not listed in the table, please consult your published in the current-year Waterfowl Digest. local newspaper. 2016 Sept. Oct. Nov. Dec. To determine the opening (a.m.) and closing (p.m.) time for any day in another Note: time zone, add the minutes shown below to the times listed in the Time Zone A • Woodcock and teal Date AM PM AM PM AM PM AM PM Hunting Hours Table. hunting hours are 1 6:28 8:35 7:00 7:43 7:36 6:55 7:12 5:31 The hunting hours listed in the table reflect Eastern Standard Time, with an sunrise to sunset. 2 6:29 8:34 7:01 7:41 7:38 6:54 7:14 5:30 adjustment for daylight saving time. If you are hunting in Gogebic, Iron, Dickinson, • Spring turkey hunting 3 6:30 8:32 7:02 7:39 7:39 6:52 7:15 5:30 or Menominee counties (Central Standard Time), you must make an additional hours are one-half 4 6:31 8:30 7:03 7:38 7:40 6:51 7:16 5:30 adjustment to the printed time by subtracting one hour.
    [Show full text]
  • DTA Scoring Form
    Daytime Astronomy SHADOWS Score Form Date ____/____/____ Student _______________________________________ Rater _________________ Problem I. (Page 3) Accuracy of results Draw a dot on this map to show where you think Tower C is. Tower C is in Eastern US Tower C is in North Eastern US Tower C is somewhere in between Pennsylvania and Maine Modeling/reasoning/observation How did you figure out where Tower C is? Matched shadow lengths of towers A and B/ pointed flashlight to Equator Tried different locations for tower C/ inferred location of tower C Matched length of shadow C/considered Latitude (distance from Equator) Matched angle of shadow C/ considered Longitude (East-West direction) Problem II. (Page 4) Accuracy of results How does the shadow of Tower A look at 10 AM and 3 PM?... Which direction is the shadow moving? 10 AM shadow points to NNW 10 AM shadow is shorter than noon shadow 3 PM shadow points to NE 3 PM shadow is longer than noon shadow Clockwise motion of shadows Modeling/reasoning/observation How did you figure out what the shadow of Tower A looks like at 10 AM and 3 PM? Earth rotation/ "Sun motion" Sunlight coming from East projects a shadow oriented to West Sunlight coming from West projects a shadow oriented to East Sunlight coming from above us projects a shadow oriented to North Sun shadows are longer in the morning than at noon Morning Sun shadows become shorter and shorter until its noon The shortest Sun shadow is at noon Sun shadows are longer in the afternoon than at noon Afternoon Sun shadows become longer and longer until it gets dark (Over, please) - 1 - 6/95 Problem III.
    [Show full text]
  • Daylight Saving Time (DST)
    Daylight Saving Time (DST) Updated September 30, 2020 Congressional Research Service https://crsreports.congress.gov R45208 Daylight Saving Time (DST) Summary Daylight Saving Time (DST) is a period of the year between spring and fall when clocks in most parts of the United States are set one hour ahead of standard time. DST begins on the second Sunday in March and ends on the first Sunday in November. The beginning and ending dates are set in statute. Congressional interest in the potential benefits and costs of DST has resulted in changes to DST observance since it was first adopted in the United States in 1918. The United States established standard time zones and DST through the Calder Act, also known as the Standard Time Act of 1918. The issue of consistency in time observance was further clarified by the Uniform Time Act of 1966. These laws as amended allow a state to exempt itself—or parts of the state that lie within a different time zone—from DST observance. These laws as amended also authorize the Department of Transportation (DOT) to regulate standard time zone boundaries and DST. The time period for DST was changed most recently in the Energy Policy Act of 2005 (EPACT 2005; P.L. 109-58). Congress has required several agencies to study the effects of changes in DST observance. In 1974, DOT reported that the potential benefits to energy conservation, traffic safety, and reductions in violent crime were minimal. In 2008, the Department of Energy assessed the effects to national energy consumption of extending DST as changed in EPACT 2005 and found a reduction in total primary energy consumption of 0.02%.
    [Show full text]
  • Impact of Extended Daylight Saving Time on National Energy Consumption
    Impact of Extended Daylight Saving Time on National Energy Consumption TECHNICAL DOCUMENTATION FOR REPORT TO CONGRESS Energy Policy Act of 2005, Section 110 Prepared for U.S. Department of Energy Office of Energy Efficiency and Renewable Energy By David B. Belzer (Pacific Northwest National Laboratory), Stanton W. Hadley (Oak Ridge National Laboratory), and Shih-Miao Chin (Oak Ridge National Laboratory) October 2008 U.S. Department of Energy Energy Efficiency and Renewable Energy Page Intentionally Left Blank Acknowledgements The Department of Energy (DOE) acknowledges the important contributions made to this study by the principal investigators and primary authors—David B. Belzer, Ph.D (Pacific Northwest National Laboratory), Stanton W. Hadley (Oak Ridge National Laboratory), and Shih-Miao Chin, Ph.D (Oak Ridge National Laboratory). Jeff Dowd (DOE Office of Energy Efficiency and Renewable Energy) was the DOE project manager, and Margaret Mann (National Renewable Energy Laboratory) provided technical and project management assistance. Two expert panels provided review comments on the study methodologies and made important and generous contributions. 1. Electricity and Daylight Saving Time Panel – technical review of electricity econometric modeling: • Randy Barcus (Avista Corp) • Adrienne Kandel, Ph.D (California Energy Commission) • Hendrik Wolff, Ph.D (University of Washington) 2. Transportation Sector Panel – technical review of analytical methods: • Harshad Desai (Federal Highway Administration) • Paul Leiby, Ph.D (Oak Ridge National Laboratory) • John Maples (DOE Energy Information Administration) • Art Rypinski (Department of Transportation) • Tom White (DOE Office of Policy and International Affairs) The project team also thanks Darrell Beschen (DOE Office of Energy Efficiency and Renewable Energy), Doug Arent, Ph.D (National Renewable Energy Laboratory), and Bill Babiuch, Ph.D (National Renewable Energy Laboratory) for their helpful management review.
    [Show full text]
  • Special Catalogue Milestones of Lunar Mapping and Photography Four Centuries of Selenography on the Occasion of the 50Th Anniversary of Apollo 11 Moon Landing
    Special Catalogue Milestones of Lunar Mapping and Photography Four Centuries of Selenography On the occasion of the 50th anniversary of Apollo 11 moon landing Please note: A specific item in this catalogue may be sold or is on hold if the provided link to our online inventory (by clicking on the blue-highlighted author name) doesn't work! Milestones of Science Books phone +49 (0) 177 – 2 41 0006 www.milestone-books.de [email protected] Member of ILAB and VDA Catalogue 07-2019 Copyright © 2019 Milestones of Science Books. All rights reserved Page 2 of 71 Authors in Chronological Order Author Year No. Author Year No. BIRT, William 1869 7 SCHEINER, Christoph 1614 72 PROCTOR, Richard 1873 66 WILKINS, John 1640 87 NASMYTH, James 1874 58, 59, 60, 61 SCHYRLEUS DE RHEITA, Anton 1645 77 NEISON, Edmund 1876 62, 63 HEVELIUS, Johannes 1647 29 LOHRMANN, Wilhelm 1878 42, 43, 44 RICCIOLI, Giambattista 1651 67 SCHMIDT, Johann 1878 75 GALILEI, Galileo 1653 22 WEINEK, Ladislaus 1885 84 KIRCHER, Athanasius 1660 31 PRINZ, Wilhelm 1894 65 CHERUBIN D'ORLEANS, Capuchin 1671 8 ELGER, Thomas Gwyn 1895 15 EIMMART, Georg Christoph 1696 14 FAUTH, Philipp 1895 17 KEILL, John 1718 30 KRIEGER, Johann 1898 33 BIANCHINI, Francesco 1728 6 LOEWY, Maurice 1899 39, 40 DOPPELMAYR, Johann Gabriel 1730 11 FRANZ, Julius Heinrich 1901 21 MAUPERTUIS, Pierre Louis 1741 50 PICKERING, William 1904 64 WOLFF, Christian von 1747 88 FAUTH, Philipp 1907 18 CLAIRAUT, Alexis-Claude 1765 9 GOODACRE, Walter 1910 23 MAYER, Johann Tobias 1770 51 KRIEGER, Johann 1912 34 SAVOY, Gaspare 1770 71 LE MORVAN, Charles 1914 37 EULER, Leonhard 1772 16 WEGENER, Alfred 1921 83 MAYER, Johann Tobias 1775 52 GOODACRE, Walter 1931 24 SCHRÖTER, Johann Hieronymus 1791 76 FAUTH, Philipp 1932 19 GRUITHUISEN, Franz von Paula 1825 25 WILKINS, Hugh Percy 1937 86 LOHRMANN, Wilhelm Gotthelf 1824 41 USSR ACADEMY 1959 1 BEER, Wilhelm 1834 4 ARTHUR, David 1960 3 BEER, Wilhelm 1837 5 HACKMAN, Robert 1960 27 MÄDLER, Johann Heinrich 1837 49 KUIPER Gerard P.
    [Show full text]
  • Schedule Book
    Monday Morning, April 26, 2021 Live Session Room Live - Session LI-MoM1 Coatings for Flexible Electronics and Bio Applications Live Session Moderators: Dr. Jean Geringer, Ecole Nationale Superieure des Mines, France, Dr. Grzegorz (Greg) Greczynski, Linköping University, Sweden, Dr. Christopher Muratore, University of Dayton, USA, Dr. Barbara Putz, Empa, Switzerland 10:00am LI-MoM1-1 ICMCTF Chairs' Welcome Address, G. Greczynski, Linköping University, Sweden; C. Muratore, University of Dayton, USA 10:15am INVITED: LI-MoM1-2 Plenary Lecture: Organic Bioelectronics – Nature Connected, M. Berggren, Linköping University, Norrköping, Sweden 10:30am 10:45am 11:00am BREAK 11:15am INVITED: LI-MoM1-6 Flexible Printed Sensors for Biomechanical Measurements, T. Ng, University of California San Diego, USA 11:30am 11:45am INVITED: LI-MoM1-8 Flexible Electronics: From Interactive Smart Skins to In vivo Applications, D. Makarov, Helmholtz-Zentrum Dresden-Rossendorf e. V. (HZDR), Institute of Ion Beam Physics and Materials Research, Germany 12:00pm 12:15pm INVITED: LI-MoM1-10 Biomimetic Extracellular Matrix Coating for Titanium Implant Surfaces to Improve Osteointegration, S. Ravindran, P. Gajendrareddy, J. Hassan, C. Huang, University of Illinois at Chicago, USA 12:30pm 12:45pm LI-MoM1-12 Closing Remarks & Thank You!, C. Muratore, University of Dayton, USA; G. Greczynski, Linköping University, Sweden, USA Monday Morning, April 26, 2021 1 10:00 AM Monday Morning, April 26, 2021 Live Session Room Live - Session LI-MoM2 New Horizons in Boron-Containing Coatings Live Session Moderators: Mr. Marcus Hans, RWTH Aachen University, Germany, Dr. Helmut Riedl, TU Wien, Institute of Materials Science and Technology, Austria 11:00am LI-MoM2-1 Welcome & Thank You to Sponsors, M.
    [Show full text]
  • Trajectory Coordinate System Information We Have Calculated the New Horizons Trajectory and Full State Vector Information in 11 Different Coordinate Systems
    Trajectory Coordinate System Information We have calculated the New Horizons trajectory and full state vector information in 11 different coordinate systems. Below we describe the coordinate systems, and in the next section we describe the trajectory file format. Heliographic Inertial (HGI) This system is Sun centered with the X-axis along the intersection line of the ecliptic (zero longitude occurs at the +X-axis) and solar equatorial planes. The Z-axis is perpendicular to the solar equator, and the Y-axis completes the right-handed system. This coordinate system is also referred to as the Heliocentric Inertial (HCI) system. Heliocentric Aries Ecliptic Date (HAE-DATE) This coordinate system is heliocentric system with the Z-axis normal to the ecliptic plane and the X-axis pointes toward the first point of Aries on the Vernal Equinox, and the Y- axis completes the right-handed system. This coordinate system is also referred to as the Solar Ecliptic (SE) coordinate system. The word “Date” refers to the time at which one defines the Vernal Equinox. In this case the date observation is used. Heliocentric Aries Ecliptic J2000 (HAE-J2000) This coordinate system is heliocentric system with the Z-axis normal to the ecliptic plane and the X-axis pointes toward the first point of Aries on the Vernal Equinox, and the Y- axis completes the right-handed system. This coordinate system is also referred to as the Solar Ecliptic (SE) coordinate system. The label “J2000” refers to the time at which one defines the Vernal Equinox. In this case it is defined at the J2000 date, which is January 1, 2000 at noon.
    [Show full text]
  • Geodetic Position Computations
    GEODETIC POSITION COMPUTATIONS E. J. KRAKIWSKY D. B. THOMSON February 1974 TECHNICALLECTURE NOTES REPORT NO.NO. 21739 PREFACE In order to make our extensive series of lecture notes more readily available, we have scanned the old master copies and produced electronic versions in Portable Document Format. The quality of the images varies depending on the quality of the originals. The images have not been converted to searchable text. GEODETIC POSITION COMPUTATIONS E.J. Krakiwsky D.B. Thomson Department of Geodesy and Geomatics Engineering University of New Brunswick P.O. Box 4400 Fredericton. N .B. Canada E3B5A3 February 197 4 Latest Reprinting December 1995 PREFACE The purpose of these notes is to give the theory and use of some methods of computing the geodetic positions of points on a reference ellipsoid and on the terrain. Justification for the first three sections o{ these lecture notes, which are concerned with the classical problem of "cCDputation of geodetic positions on the surface of an ellipsoid" is not easy to come by. It can onl.y be stated that the attempt has been to produce a self contained package , cont8.i.ning the complete development of same representative methods that exist in the literature. The last section is an introduction to three dimensional computation methods , and is offered as an alternative to the classical approach. Several problems, and their respective solutions, are presented. The approach t~en herein is to perform complete derivations, thus stqing awrq f'rcm the practice of giving a list of for11111lae to use in the solution of' a problem.
    [Show full text]
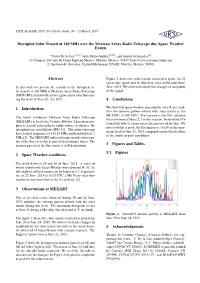
  • Disrupted Solar Transit at 140 Mhz Over the Mexican Array Radio Telescope Due Space Weather Events
    URSI AP-RASC 2019, New Delhi, India; 09 - 15 March 2019 Disrupted Solar Transit at 140 MHz over the Mexican Array Radio Telescope due Space Weather Events *Victor De la Luz(1)(2), Julio Mejia-Ambriz(1)(2), and Americo Gonzalez(2) (1) Conacyt, Servicio de Clima Espacial Mexico, Morelia, Mexico. 58190. http://www.sciesmex.unam.mx (2) Instituto de Geofisica, Unidad Michoacan, UNAM, Morelia, Mexico. 58190. Abstract Figure 2 show two solar transits centered at peak, for 22 (green line, quiet) and 26 (blue line, close to the solar flare) In this work we present the records of the disrupted so- June, 2015. We observed clearly the changes of amplitude lar transits at 140 MHz at Mexican Array Radio Telescope of the signal. (MEXART) related with active regionsand a solar flare dur- ing the week of June 20 - 26, 2015. 4 Conclusions 1 Introduction We show that space weather, in particular solar flares, mod- ifies the antenna pattern related with solar transit in the MEXART at 140 MHz. The increase in the flux saturated The transit instrument Mexican Array Radio Telescope the instrument at June 22. For this reasson, we used the 5Th (MEXART) is located in Coeneo, Mexico. Their main pro- lateral left lobe to characterize the increase of the flux. We pose is record extra-galactic radio source to observe the observed that at peak, the flux increases 16 mV in the max- interplanetary scintillation (IPS) [3]. The radio telescope imum level at June 22, 2015 compared against the baseline have central frequency of 139.65 MHz and bandwidth of 2 of the transit in quiet conditions.
    [Show full text]