Crystalline Silicon Solar Cells
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Life Cycle Analysis of High-Performance Monocrystalline Silicon Photovoltaic Systems: Energy Payback Times and Net Energy Production Value
27th European Photovoltaic Solar Energy Conference and Exhibition LIFE CYCLE ANALYSIS OF HIGH-PERFORMANCE MONOCRYSTALLINE SILICON PHOTOVOLTAIC SYSTEMS: ENERGY PAYBACK TIMES AND NET ENERGY PRODUCTION VALUE Vasilis Fthenakis1,2, Rick Betita2, Mark Shields3, Rob Vinje3, Julie Blunden3 1 Brookhaven National Laboratory, Upton, NY, USA, tel. 631-344-2830, fax. 631-344-3957, [email protected] 2Center for Life Cycle Analysis, Columbia University, New York, NY 10027, USA 3SunPower Corporation, San Jose, CA, USA ABSTRACT: This paper summarizes a comprehensive life cycle analysis based on actual process data from the manufacturing of Sunpower 20.1% efficient modules in the Philippines and other countries. Higher efficiencies are produced by innovative cell designs and material and energy inventories that are different from those in the production of average crystalline silicon panels. On the other hand, higher efficiencies result to lower system environmental footprints as the system area on a kW basis is smaller. It was found that high efficiencies result to a net gain in environmental metrics (i.e., Energy Payback Times, GHG emissions) in comparison to average efficiency c-Si modules. The EPBT for the Sunpower modules produced in the Philippines and installed in average US or South European insolation is only 1.4 years, whereas the lowest EPBT from average efficiency c-Si systems is ~1.7 yrs. To capture the advantage of high performance systems beyond their Energy Payback Times, we introduced the metric of Net Energy Production Value (NEPV), which shows the solar electricity production after the system has “paid-off” the energy used in its life-cycle. The SunPower modules are shown to produce 45% more electricity than average efficiency (i.e., 14%) c-Si PV modules. -

New Challenges and Possibilities for Silicon Based Solar Cells
1 New challenges and possibilities for silicon based solar cells Marisa Di Sabatino Dept of Materials Science and Engineering NTNU 2 Outline -What is a solar cell? -How does it work? -Silicon based solar cells manufacturing -Challenges and Possibilities -Concluding remarks 3 What is a solar cell? • It is a device that converts the energy of the sunlight directly into electricity. CB PHOTON Eph=hc/λ VB Electron-hole pair 4 How does a solar cell work? 5 How does a solar cell work? Current Semiconductor Eg + - P-n junction Metallic contacts Turid Worren Reenaas 6 How does a solar cell work? - Charge generation (electron-hole pairs) - Charge separation (electric field) - Charge transport 7 - Charge generation (electron-hole pairs) - Charge separation (electric field) - Charge transport Eph>>Eg Eph<<Eg Eph>Eg Eg CB Eph VB 8 - Charge generation (electron-hole pairs) - Charge separation (electric field) - Charge transport p-type C - - - - Fermi level - + + + + + n-type n-p junction v + - Electric field 9 - Charge generation (electron-hole pairs) - Charge separation (electric field) - Charge transport Back and front side of a silicon solar cell 10 Semiconductors Materials for solar cells 11 Why Silicon? Silicon: abundant, cheap, well-known technology 12 Silicon solar cell value chain 13 Silicon solar cells value chain From sand to solar cells… Raw Materials Efficiency Crystallization Isc, Voc, FF Feedstock Solar cell process Photo: Melinda Gaal 14 Multicrystalline silicon solar cells Directional solidification 15 Monocrystalline silicon solar cells Czochralski process 16 Crystallization methods for PV silicon • Multicrystalline silicon ingots: – Lower cost than monocrystalline – More defects (dislocations and impurities) • Monocrystalline silicon ingots: – Higher cost and lower yield – Oxygen related defects – Structure loss 17 Czochralski PV single crystal growth • Dominating process for single crystals • Both p (B-doped) and n (P-doped) type crystals • Growth rate 60 mm/h Challenges: •Productivity low due to slow growth, long cycle time.. -

15Th Workshop on Crystalline Silicon Solar Cells and Modules: Materials and Processes
A national laboratory of the U.S. Department of Energy Office of Energy Efficiency & Renewable Energy National Renewable Energy Laboratory Innovation for Our Energy Future th Proceedings 15 Workshop on Crystalline NREL/BK-520-38573 Silicon Solar Cells and Modules: November 2005 Materials and Processes Extended Abstracts and Papers Workshop Chairman/Editor: B.L. Sopori Program Committee: M. Al-Jassim, J. Kalejs, J. Rand, T. Saitoh, R. Sinton, M. Stavola, R. Swanson, T. Tan, E. Weber, J. Werner, and B. Sopori Vail Cascade Resort Vail, Colorado August 7–10, 2005 NREL is operated by Midwest Research Institute ● Battelle Contract No. DE-AC36-99-GO10337 th Proceedings 15 Workshop on Crystalline NREL/BK-520-38573 Silicon Solar Cells and Modules: November 2005 Materials and Processes Extended Abstracts and Papers Workshop Chairman/Editor: B.L. Sopori Program Committee: M. Al-Jassim, J. Kalejs, J. Rand, T. Saitoh, R. Sinton, M. Stavola, R. Swanson, T. Tan, E. Weber, J. Werner, and B. Sopori Vail Cascade Resort Vail, Colorado August 7–10, 2005 Prepared under Task No. WO97G400 National Renewable Energy Laboratory 1617 Cole Boulevard, Golden, Colorado 80401-3393 303-275-3000 • www.nrel.gov Operated for the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy by Midwest Research Institute • Battelle Contract No. DE-AC36-99-GO10337 NOTICE This report was prepared as an account of work sponsored by an agency of the United States government. Neither the United States government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or `process disclosed, or represents that its use would not infringe privately owned rights. -

Research Into Fabrication and Popularization of Organic Thin Film Solar Cells, Chemical Engineering Transactions, 55, 25-30 DOI:10.3303/CET1655005 26
25 A publication of CHEMICAL ENGINEERING TRANSACTIONS VOL. 55, 2016 The Italian Association of Chemical Engineering Online at www.aidic.it/cet Guest Editors: Tichun Wang, Hongyang Zhang, Lei Tian Copyright © 2016, AIDIC Servizi S.r.l., ISBN 978-88-95608-46-4; ISSN 2283-9216 DOI: 10.3303/CET1655005 Research into Fabrication and Popularization of Organic Thin Film Solar Cells Bin Zhang*a, Yan Lia, Shanlin Qiaob, Le Lic, Zhanwen Wanga a Hebei Chemical & Pharmaceutical College, No. 88 Fangxing Road, Shijiazhuang, Hebei Province, China; b Qingdao Institute of Bioenergy and Bioprocess Technology, Chinese Academy of Sciences, No. 189 Songling Road, Qingdao, Shandong Province, China c Shijiazhuang Naienph Chemical Technology Co., Ltd, No. 12 Shifang Road, Shijiazhuang, Hebei Province, China. [email protected] An analysis was conducted herein on the research status of several popular solar cells at the present stage, including silicon solar cell, thin film photovoltaic cell, and dye-sensitized solar cell (DSSC). In doing so, we concluded that the current situations provide a favorable objective environment for the popularization of organic thin film solar cells. Finally, we reviewed the merits and demerits of the organic thin film solar cell together with the major research focus on and progress of it, and summarized obstacles to and development trails of the popularization of organic thin film solar cells. 1. Introduction As the energy crisis further deepens in the 21st century, the existing development level for solar cells has already failed to satisfy increasing social demands for energy. This phenomenon is mainly reflected in the costly high-purity silicon solar panels, in the defects at new amorphous silicon (a-Si) during energy conversion, and in the limited theoretical energy conversion efficiency (around 25%) of silicon solar panels as well. -
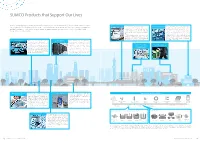
SUMCO Products That Support Our Lives
SUMCO Products that Support Our Lives SUMCO manufactures silicon wafers, a key material in semiconductor devices. Semiconductor devices that use SUMCO’s silicon Trains, Bullet Trains Devices called power semiconductors are Medical Equipments In the medical field, medical equipment has wafers support our lives in a variety of ways, from electronic devices around us such as mobile phones, computers, smartphones used to control electric power. These devices continued to evolve, with the advent of high- and digital appliances to automobiles, medical equipment, industrial machinery control units, as well as the control of public are technically complex and require reliable precision diagnostic imaging equipment and transportation and infrastructure. control of large amounts of power and power surgery robots capable of precise control. saving performance, making this a specialized A large number of silicon wafers are used field. in these medical devices, and the silicon Power supply control for heavy electric wafers that serve as their substrates require machinery, in particular, such as electric trains high reliability, especially as human lives are that use power of over 1000V, requires special involved. SUMCO’s silicon wafers contribute to know-how for the silicon wafers, as well. the advance of medicine. Automobiles Numerous semiconductor devices Data Centers With smartphones and computers are at work inside motor vehicles. An (Server Rooms) becoming increasingly sophisticated, extremely high level of quality and vast quantities of data in the form of Power Generation reliability is required for silicon wafers high-quality photographs and vid- Smart Card Devices Facilities and Public to be used for motor control in electric eos are being processed in the cloud vehicles (EV) and hybrid vehicles (HV/ and stored in data centers. -

A New Slicing Method of Monocrystalline Silicon Ingot by Wire EDM
cf~ Paper International Journal of Electrical Machining, No. 8, January 2003 A New Slicing Method of Monocrystalline Silicon Ingot by Wire EDM Akira OKADA *, Yoshiyuki UNO *, Yasuhiro OKAMOTO*, Hisashi ITOH* and Tameyoshi HlRANO** (Received May 28, 2002) * Department of Mechanical Engineering, Okayama University, Okayama 700-8530, Japan ** Toyo Advanced Technologies Co., Ltd., Hiroshima 734-8501, Japan Abstract Monocrystalline silicon is one of the most important materials in the semiconductor industry because of its many excellent properties as a semiconductor. In the manufacturing process of silicon wafers, inner diameter(lD) blade and multi wire saw have conventionally been used for slicing silicon ingots. However, some problems in efficiency, accuracy, slurry treatment and contamination are experienced when applying this method to large scale wafers of 12 or 16 inch diameter expected to be used in the near future. Thus, the improvement of conventional methods or a new slicing method is strongly required. In this study, the possibility of slicing a silicon ingot by wire EDM was discussed and the machining properties were experimentally investigated. A silicon wafer used as substrate for epitaxial film growth has low resistivity in the order of 0.01 g .cm, which makes it possible to cut silicon ingots by wire EDM. It was clarified that the new wire EDM has potential for application as a new slicing method, and that the surface roughness using this method is as small as that using the conventional multi wire saw method. Moreover, it was pointed out that the contamination due to the adhesion and diffusion of wire electrode material into the machined surface can be reduced by wire EDM under the condition of low current and long discharge duration. -

A Study on the Countermeasures and Suggestions of Technology
4th International Education, Economics, Social Science, Arts, Sports and Management Engineering Conference (IEESASM 2016) A Study on the Countermeasures and Suggestions of Technology Transfer in the Solar Cells Industry in China Lvcheng Lia, Guoping Chengb School of Management, Wuhan University of Technology, Wuhan 430070, China [email protected], [email protected] Keywords: solar cells; technology transfer; countermeasures and suggestions Abstract. This paper analyzes the development and industrialization of solar cells of three generations: mono-crystalline silicon and polycrystalline silicon solar cell, thin-film solar cell and nanocrystalline solar cell. It is believed that technology transfer and university-industry collaboration play important roles in the solar cells industry; and put forward reasonable suggestions for improvements from the aspects of financial subsidies, intellectual property, risk compensation system, technology transfer intermediary and cultivation of talents. 1. Introduction New energy technology is one of the most important topics for human's development in the 21st century. The traditional energy sources such as oil and natural gas, have some serious problems like pollution and storage, which cannot satisfy the requirements of human beings and conflict with the sustainable development. As an important component of new energy, solar energy exhibits the advantages of low carbon emission, clean production, flexibility and renewability, which is ideal to be applied as a new alternative energy and has become the focus of the scientific community and industry. Presently, the solar cells have already been used in national defense, communications, computers, transportation and many other fields. Due to China's unique geographical advantages, to develop the solar energy is the trend of the time. -

Crystalline Silicon Photovoltaic Module Manufacturing
Crystalline Silicon Photovoltaic Module Manufacturing Costs and Sustainable Pricing: 1H 2018 Benchmark and Cost Reduction Road Map Michael Woodhouse, Brittany Smith, Ashwin Ramdas, and Robert Margolis National Renewable Energy Laboratory NREL is a national laboratory of the U.S. Department of Energy Technical Report Office of Energy Efficiency & Renewable Energy NREL/TP-6A20-72134 Operated by the Alliance for Sustainable Energy, LLC Revised February 2020 This report is available at no cost from the National Renewable Energy Laboratory (NREL) at www.nrel.gov/publications. Contract No. DE-AC36-08GO28308 Crystalline Silicon Photovoltaic Module Manufacturing Costs and Sustainable Pricing: 1H 2018 Benchmark and Cost Reduction Road Map Michael Woodhouse, Brittany Smith, Ashwin Ramdas, and Robert Margolis National Renewable Energy Laboratory Suggested Citation Woodhouse, Michael. Brittany Smith, Ashwin Ramdas, and Robert Margolis. 2019. Crystalline Silicon Photovoltaic Module Manufacturing Costs and Sustainable Pricing: 1H 2018 Benchmark and Cost Reduction Roadmap. Golden, CO: National Renewable Energy Laboratory. https://www.nrel.gov/docs/fy19osti/72134.pdf. NREL is a national laboratory of the U.S. Department of Energy Technical Report Office of Energy Efficiency & Renewable Energy NREL/TP-6A20-72134 Operated by the Alliance for Sustainable Energy, LLC Revised February 2020 This report is available at no cost from the National Renewable Energy National Renewable Energy Laboratory Laboratory (NREL) at www.nrel.gov/publications. 15013 Denver West Parkway Golden, CO 80401 Contract No. DE-AC36-08GO28308 303-275-3000 • www.nrel.gov NOTICE This work was authored by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. -

Thin Crystalline Silicon Solar Cells Based on Epitaxial Films Grown at 165 °C by RF-PECVD Romain Cariou, Martin Labrune, Pere Roca I Cabarrocas
Thin crystalline silicon solar cells based on epitaxial films grown at 165 °C by RF-PECVD Romain Cariou, Martin Labrune, Pere Roca I Cabarrocas To cite this version: Romain Cariou, Martin Labrune, Pere Roca I Cabarrocas. Thin crystalline silicon solar cells based on epitaxial films grown at 165 °C by RF-PECVD. Solar Energy Materials and Solar Cells, Elsevier, 2011, 95 (8), pp.2260-2263. 10.1016/j.solmat.2011.03.038. hal-00749873v3 HAL Id: hal-00749873 https://hal-polytechnique.archives-ouvertes.fr/hal-00749873v3 Submitted on 14 May 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Thin crystalline silicon solar cells based on epitaxial films grown at 165°C by RF-PECVD Romain Carioua),*, Martin Labrunea),b), P. Roca i Cabarrocasa) aLPICM-CNRS, Ecole Polytechnique, 91128 Palaiseau, France bTOTAL S.A., Gas & Power, R&D Division, Tour La Fayette, 2 Place des Vosges, La Défense 6, 92 400 Courbevoie, France Keywords Low temperature, Epitaxy; PECVD; Si thin film; Solar cell Abstract We report on heterojunction solar cells whose thin intrinsic crystalline absorber layer has been obtained by plasma enhanced chemical vapor deposition at 165°C on highly doped p-type (100) crystalline silicon substrates. -

Sliver Cells in Thermophotovoltaic Systems
Sliver Cells in Thermophotovoltaic Systems Niraj Lal A thesis submitted for the degree of Bachelor of Science with Honours in Physics at The Australian National University May, 2007 ii Declaration This thesis is an account of research undertaken between July 2006 and May 2007 at the Centre for Sustainable Energy Systems and the Department of Physics, The Australian National University, Canberra, Australia. Except where acknowledged in the customary manner, the material presented in this thesis is, to the best of my knowledge, original and has not been submitted in whole or part for a degree in any university. Niraj Lal May, 2007 iii iv Acknowledgements There are a number of many people without whom this thesis would not have been possible. First and foremost I would like to thank my supervisor Professor Andrew Blakers, for giving me the freedom to go ‘where the science took me’, for being extremely generous with his knowledge, and for his advice to go for a run when writing got difficult. Learning about solar energy from Andrew has been an inspiring experience. I would also like to acknowledge the support of the ANU Angus Nicholson Honours Scholarship for passion in science. I hope that this work can, in some way, honour the memory and passion of Dr. Nicholson. Thankyou to all of the friendly solar community at ANU, in particular Dr. Evan Franklin who introduced me to the wonderful world of programming. To the DE PhD students, thankyou (I think) for making me a better kicker player. Thanks also to my friendly Swiss officemate Lukas who helped me with Matlab. -

Silicon Epitaxy on Textured Double Layer Porous Silicon by LPCVD
Physica B 405 (2010) 3852–3856 Contents lists available at ScienceDirect Physica B journal homepage: www.elsevier.com/locate/physb Silicon epitaxy on textured double layer porous silicon by LPCVD Hong Cai a, Honglie Shen a,n, Lei Zhang a, Haibin Huang a, Linfeng Lu a, Zhengxia Tang a, Jiancang Shen b a College of Materials Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China b National Laboratory of Solid State Microstructure and Department of Physics, Nanjing University, Nanjing 210093, China article info abstract Article history: Epitaxial silicon thin film on textured double layer porous silicon (DLPS) was demonstrated. The Received 2 April 2010 textured DLPS was formed by electrochemical etching using two different current densities on the Received in revised form silicon wafer that are randomly textured with upright pyramids. Silicon thin films were then grown on 13 May 2010 the annealed DLPS, using low-pressure chemical vapor deposition (LPCVD). The reflectance of the DLPS Accepted 7 June 2010 and the grown silicon thin films were studied by a spectrophotometer. The crystallinity and topography of the grown silicon thin films were studied by Raman spectroscopy and SEM. The reflectance results Keywords: show that the reflectance of the silicon wafer decreases from 24.7% to 11.7% after texturing, and after Porous silicon the deposition of silicon thin film the surface reflectance is about 13.8%. SEM images show that the Surface texture epitaxial silicon film on textured DLPS exhibits random pyramids. The Raman spectrum peaks near Silicon epitaxy 521 cmÀ1 have a width of 7.8 cmÀ1, which reveals the high crystalline quality of the silicon epitaxy. -

Solar Power for Ham Radio
Solar Power for Ham Radio KK4LTQ [email protected] http://kk4ltq.com/solar/SolarPower.zip The key facts about each type of solar cell: Monocrystalline Overview and Appearance This is the oldest and most developed of the three technologies. Monocrystalline panels as the name suggests are created from a single continuous crystal structure. A Monocrystalline panel can be identified from the solar cells which all appear as a single flat color. Construction They are made through the Czochralski method where a silicon crystal ‘seed’ is placed in a vat of molten silicon. The seed is then slowly drawn up with the molten silicon forming a solid crystal structure around the seed known as an ingot. The ingot of solid crystal silicon that is formed is then finely sliced ingot what is known as a silicon wafer. This is then made into a cell. The Czochralski process results in large cylindrical ingots. Four sides are cut out of the ingots to make silicon wafers. A significant amount of the original silicon ends up as waste. The key facts about each type of solar cell: Polycrystalline Overview and Appearance Polycrystalline or Multicrystalline are a newer technology and vary in the manufacturing process. Construction Polycrystalline also start as a silicon crystal ‘seed’ placed in a vat of molten silicon. However, rather than draw the silicon crystal seed up as with Monocrystalline the vat of silicon is simply allowed to cool. This is what forms the distinctive edges and grains in the solar cell . Polycrystalline cells were previously thought to be inferior to Monocrystalline because they were slightly less efficient, however, because of the cheaper method by which they can be produced coupled with only slightly lower efficiencies they have become the dominant technology on the residential solar panels market.