DOCSLIB.ORG

Linear Regression and the Bias Variance Tradeoff

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Linear Regression and the Bias Variance Tradeoff Linear Regression and the Bias Variance Tradeoff Guest Lecturer Joseph E. Gonzalez slides available here: h"p://;nyurl.com/re1lecture Simple Linear Regression Y X Response Variable Covariate Linear Model: Y = mX + b Slope Intercept (bias) MoHvaon • Ine of t.e most widely used tec.niMues • Nundamental to many larger models – 4enerali:ed Linear Codels – Collaborave filtering • Easy to interpret • EPcient to solve CulHple Linear Regression 2.e Regression Codel • Nor a single data point (x,y): Endependent 0ariable Response 0ariable F0ector) FScalar) Ibserve: FCondiHon) R y x ∈ Rp y ∈ R • 6oint Probability: Siscriminave p(x, y)=p(x)p(y|x) Model The Linear Model Vector of Parameters Vector of Covariates T Scalar Real Value Response y = ✓ x + ✏ Noise + b p Noise Model: ∼ 2 Linear Combina;on ✏ N(0, σ ) θixi of Covariates X i=1 What about bias/intercept term? Define: xp+1 =1 Then redefine p := p+1 for notaonal simplicity CondiHonal Likeli.ood pFy|R) • CondiHoned on R: Constant Normal Sistribuon T 2 y = ✓ x + ✏ ∼ N(0, σ ) Mean 0ariance • CondiHonal distribuHon of Y: T 2 Y ∼ N(θ x, σ ) 1 (y θT x)2 p(y x)= exp − 2 | σ√2π ✓− 2σ ◆ Parameters and Random Variables Parameters T 2 y ∼ N(θ x, σ ) • CondiHonal distribuHon of y: – /ayesian: parameters as random variables 2 p(y|x, θ, σ ) – NreMuenHst: parameters as Funknown) constants pθ,σ2 (y|x) So far _ A E’m lonely * B2 B1 Independent and IdenHcally Sistributed Fiid) Sata • Nor n data points: D = {(x1,y1),...,(xn,yn)} n = {(xi,yi)}i=1 Plate Diagram Endependent 0ariable Response 0ariable F0ector) FScalar) Ri yi p xi ∈ R yi ∈ R i ∈ {1,...,n} Joint Probability x y i i n • For n data points independent and iden;cally distributed (iid): n p(D)=Y p(xi,yi) i=1 n = Y p(xi)p(yi|xi) i=1 RewriHng wit. CatriR Totaon n • Represent data D = {(xi,yi)}i=1 as: Covariate FSesign) Response Matrix 0ector n x1 n y1 x2 y2 X = ∈ Rnp Y = ∈ Rn ... Assume X . xn .as rank p Fnot degenerate) yn p 1 RewriHng wit. CatriR Totaon • RewriHng t.e model using matrix operaons: Y = X✓ + ✏ Y X Y X θ ✏ p n n n 1 1 p EsHmang t.e Codel • 4iven data .ow can we esHmate aW Y = X✓ + ✏ • Construct maximum likeli.ood esHmator FCLE): – Serive t.e lo)blikeli.ood – Nind aMLE t.at maximi:es lo)blikeli.ood • AnalyHcally: Take derivave and set X c • Eteravely: FStoc.asHc) gradient descent Joint Probability x y i i n • For n data points: n p(D)=Y p(xi,yi) i=1 n “1” i i i Discriminave = Y p(x )p(y |x ) Model i=1 Defining the Likelihood pθ(y x)= | T 2 xi yi 1 (y θ x) exp − 2 n σ√2π ✓− 2σ ◆ n L(θ|D)=Y pθ(yi|xi) i=1 n T 2 1 (yi θ xi) = exp − √ 2σ2 iY=1 σ 2π ✓− ◆ n 1 1 T 2 = n exp − (yi − θ xi) n 2 2 σ (2π) 2σ i=1 ! X Maximizing the Likelihood • Want to compute: θˆMLE = arg max L(θ|D) θ∈Rp • To simplify the calculaons we take the log: 1 θˆMLE = arg max log L(θ|D) 1 2 3 4 5 θ∈Rp -1 -2 which does not affect the maximizaon because log is a monotone funcHon. n θ 1 1 θT 2 L( |D)= n exp − 2 (yi − xi) σn π 2 σ (2 ) 2 i=1 ! X • Take the log: n n n 1 T 2 θ σ π 2 θ log L( |D)=− log( (2 ) ) − σ2 X(yi − xi) 2 i=1 • Removing constant terms with respect to θ: n T 2 log L(θ)=− X(yi − θ xi) i=1 Monotone FuncHon FEasy to maximize) n T 2 log L(θ)=− X(yi − θ xi) i=1 • Want to compute: θˆMLE = arg max log L(θ|D) θ∈Rp • Plugging in log‐likelihood: n T 2 θˆMLE = arg max − (yi − θ xi) θ∈Rp X i=1 n T 2 θˆMLE = arg max − (yi − θ xi) θ∈Rp X i=1 • Dropping the sign and flipping from maximizaon to minimizaon: n T 2 θˆMLE = arg min (yi − θ xi) θ∈Rp X i=1 Minimize Sum (Error)2 • Gaussian Noise Model Squared Loss – Least Squares Regression Pictorial Interpretaon of Squared Error y x Maximizing the Likelihood (Minimizing the Squared Error) n T 2 θˆMLE = arg min (yi − θ xi) θ∈Rp X i=1 − log L(θ) Convex FuncHon Slope = 0 θ ˆ θMLE • Take the gradient and set it equal to zero Minimizing the Squared Error n T 2 θˆMLE = arg min (yi − θ xi) θ∈Rp X i=1 • Taking the gradient n T 2 −rθ log L(θ)=rθ X(yi − θ xi) i=1 n T Chain Rule = −2 X(yi − θ xi)xi i=1 n n T = −2 X yixi +2X(θ xi)xi i=1 i=1 • RewriHng t.e gradient in matrix form: n n T −rθ log L(θ)=−2 X yixi +2X(θ xi)xi i=1 i=1 T T = −2X Y +2X Xθ • To make sure t.e lo)blikeli.ood is convex compute t.e second derivave Fgessian) 2 T −r log L(θ)=2X X • Ef X is full rank t.en XTX is posiHve definite and t.erefore aMLE is t.e minimum – Address t.e degenerate cases wit. regulari:aon T T −rθ log L(θ)=−2X y +2X Xθ =0 • Sehng gradient eMual to c and solve for aMLE: T T (X X)θˆMLE = X Y Normal Equaons T −1 T (Write on θˆMLE =(X X) X Y board) n p b1 n 1 p X Geometric Interpretaon • View the MLE as finding a projecHon on colFB) – Sefine t.e esHmator: Yˆ = Xθ – Ibserve t.at j is in colFB) • linear combinaon of cols of B – Uant to j closest to Y • Emplies FAbjG normal to B T T X (Y − Yˆ )=X (Y − Xθ)=0 ⇒ XT Xθ = XT Y ConnecHon to PseudobEnverse T −1 T θˆMLE =(X X) X Y CoorebPenrose X† Psuedoinverse • 4enerali:aon of t.e inverse: – Consider t.e case w.en B is sMuare and inverHble: T 1 T 1 T 1 T 1 X† =(X X)− X = X− (X )− X = X− ‐1 – U.ic. implies aMLEX X Y t.e soluHon to B a X Y w.en X is sMuare and inverHble CompuHng t.e CLE T −1 T θˆMLE =(X X) X Y • Not typically solved by inverHng XTX • Solved using direct met.ods: C.olesky factori:aon: – or use the • n7 to a factor of 2 faster built‐in solver – oR factori:aon: in your math library. • More numerically stable R: solve(Xt %*% X, Xt %*% y) • Solved using various iterave met.ods: – prylov subspace met.ods – FStoc.asHc) 4radient Sescent .qp://www.seas.ucla.edu/rvandenbe/1cs/lectures/qr.pdf Cholesky Factorizaon T T solve (X X)θˆMLE = X Y ˆ θMLE C d 2 • Compute symm. matrix C = XT X O(np ) • Compute vector d = XT Y O(np) T • Cholesky Factorizaon LL = C O(p3) – L is lower triangular 2 • Forward subs. to solve: Lz = d O(p ) T ˆ 2 • Backward subs. to solve: L θMLE = z O(p ) ConnecHons to graphical model inference: .qp://ssg.mit.edu/rwillsky/publ_pdfs/1uvtpub_MLR.pdf and .qp://yaroslavvb.blogspot.com/2c11/c2/iuncHon‐treesbin‐numericalbanalysis.html wit. illustraons Solving 2riangular System A11 A12 A1s A1w R1 b1 A22 A2s A2w R2 b2 l X Ass Asw Rs bs Aww Rw bw Solving 2riangular System A11R1 A12R2 A1sRs A1wRw b1 R1Xb1bA12R2bA1sRsbA1wRw A11 A22R2 A2sRs A2wRw b2 R2Xb2bA2sRsbA2wRw A22 AssRs AswRw bs RsXFbsbAswRw) Ass AwwRw bw RwXbw /Aww Distributed Direct SoluHon FCapbReduce) T −1 T θˆMLE =(X X) X Y • SistribuHon computaons of sums: p n = T = T 2 p C X X X xixi O(np ) i=1 1 n T p d = X y = X xiyi O(np) i=1 3 • Solve system C aMLE X d on master. O(p ) Gradient Descent: What if p is large? (e.g., n/2) • The cost of O(np2) = O(n3) could by prohibiHve • SoluHon: Eterave Cet.ods – 4radient Sescent: For τ from 0 until convergence τ τ τ θ( +1) = θ( ) − ρ(τ)r log L(θ( )|D) Learning rate 4radient Sescent Ellustrated: − log L(θ) θ(0) Slope X c θ(1) θ(2)θ(3) (3) ˆ θ = θMLE ConveR NuncHon θ Gradient Descent: What if p is large? (e.g., n/2) • The cost of O(np2) = O(n3) could by prohibiHve • SoluHon: Eterave Cet.ods – 4radient Sescent: For τ from 0 until convergence τ τ τ θ( +1) = θ( ) − ρ(τ)r log L(θ( )|D) n (τ) 1 (τ)T = θ + ρ(τ) (yi − θ xi)xi O(np) n X i=1 • Can we do beSerW EsHmate of t.e 4radient StochasHc 4radient Sescent • Construct noisy esHmate of t.e gradient: For τ from 0 until convergence 1) pick a random i 2) (τ+1) (τ) (τ)T θ = θ + ρ(τ)(yi − θ xi)xi O(p) • SensiHve to c.oice of xFy) typically FxFy)X1/y) • Also known as LeastbCeanbSMuares FLCS) • Applies to streaming data O(p) storage Nihng Tonblinear Sata • U.at if Y .as a nonblinear responseW 2.0 1.5 1.0 0.5 1 2 3 4 5 6 -0.5 -1.0 -1.5 • Can we sHll use a linear modelW Transforming the Feature Space • Transform features xi xi =(Xi,1,Xi,2,...,Xi,p) • By applying non‐linear transformaon ϕ: φ : Rp → Rk • Example: 2 k φ(x)={1,x,x ,...,x } – others: splines, radial basis funcHonsm _ – Expert engineered features Fmodeling) UnderbOhng 81.< 81., x< 2 2 1 1 1 2 3 4 5 6 1 2 3 4 5 6 -1 -1 -2 -2 Out[380]= 2 3 2 3 4 5 91., x, x , x = 91., x, x , x , x , x = 2 2 1 1 1 2 3 4 5 6 1 2 3 4 5 6 -1 -1 -2 -2 OverbOhng Really IverbOhn)z 2 3 4 5 6 7 8 9 10 11 12 13 14 91., x, x , x , x , x , x , x , x , x , x , x , x , x , x = 2 1 1 2 3 4 5 6 -1 -2 • Errors on training data are small • /ut errors on new points are likely to be large What if I train on different data? Low Variability: 2 3 2 3 2 3 91., x, x , x = 91., x, x , x = 91., x, x , x = 2 2 2 1 1 1 1 2 3 4 5 6 -1 1 2 3 4 5 6 1 2 3 4 5 6 -1 -1 -1 -2 -2 -2 High Variability 2 3 4 5 6 7 8 9 10 11 12 13 14 2 3 4 5 6 7 8 9 10 11 12 13 14 2 3 4 5 6 7 8 9 10 11 12 13 14 91., x, x , x , x , x , x , x , x , x , x , x , x , x , x = 91., x, x , x , x , x , x , x , x , x , x , x , x , x , x = 91., x, x , x , x , x , x , x , x , x , x , x , x , x , x = 2 2 2 1 1 1 1 2 3 4 5 6 -1 1 2 3 4 5 6 1 2 3 4 5 6 -1 -1 -1 -2 -2 -2 Bias‐Variance Tradeoff • So far we have minimized the error (loss) with respect to training data – Low training error does not imply good expected performance: over‐fiAn1 • We would like to reason about the eBpected loss (Credic;on RisE) over: – Training Data: {(y1, x1), …, (yn, xn)} – Test point: (y*, x*) • We will decompose the expected loss into: E 2 2 D,(y∗,x∗) ⇥(y∗ − f(x∗|D)) ⇤ = Noise + Bias + Variance • Define (unobserved) the true model (h): Assume 0 mean noise y∗ = h(x∗)+✏∗ [bias goes in h(x*)] • Completed the squares with: h(x∗)=h∗ E 2 D,(y∗,x∗) ⇥(y∗ − f(x∗|D)) ⇤ Expected Loss E 2 = D,(y∗,x∗) ⇥(y∗ − h(x∗)+h(x∗) − f(x∗|D)) ⇤ a b 2 2 2 (a + b) = a + b +2ab E 2 E 2 = ✏∗ ⇥(y∗ − h(x∗)) ⇤ + D ⇥(h(x∗) − f(x∗|D)) ⇤ E +2 D,(y∗,x∗) [y∗h∗ − y∗f∗ − h∗h∗ + h∗f∗] • Define (unobserved) the true model (h): y∗ = h(x∗)+✏∗ • Completed the squares with: h(x∗)=h∗ E 2 D,(y∗,x∗) ⇥(y∗ − f(x∗|D)) ⇤ Expected Loss E 2 = D,(y∗,x∗) ⇥(y∗ − h(x∗)+h(x∗) − f(x∗|D)) ⇤ E 2 E 2 = ✏∗ ⇥(y∗ − h(x∗)) ⇤ + D ⇥(h(x∗) − f(x∗|D)) ⇤ E +2 D,(y∗,x∗) [y∗h∗ − y∗f∗ − h∗h∗ + h∗f∗] SubsHtute defn.
Load more

Recommended publications
  • A Generalized Linear Model for Principal Component Analysis of Binary Data
    A Generalized Linear Model for Principal Component Analysis of Binary Data Andrew I. Schein Lawrence K. Saul Lyle H. Ungar Department of Computer and Information Science University of Pennsylvania Moore School Building 200 South 33rd Street Philadelphia, PA 19104-6389 {ais,lsaul,ungar}@cis.upenn.edu Abstract they are not generally appropriate for other data types. Recently, Collins et al.[5] derived generalized criteria We investigate a generalized linear model for for dimensionality reduction by appealing to proper- dimensionality reduction of binary data. The ties of distributions in the exponential family. In their model is related to principal component anal- framework, the conventional PCA of real-valued data ysis (PCA) in the same way that logistic re- emerges naturally from assuming a Gaussian distribu- gression is related to linear regression. Thus tion over a set of observations, while generalized ver- we refer to the model as logistic PCA. In this sions of PCA for binary and nonnegative data emerge paper, we derive an alternating least squares respectively by substituting the Bernoulli and Pois- method to estimate the basis vectors and gen- son distributions for the Gaussian. For binary data, eralized linear coefficients of the logistic PCA the generalized model's relationship to PCA is anal- model. The resulting updates have a simple ogous to the relationship between logistic and linear closed form and are guaranteed at each iter- regression[12]. In particular, the model exploits the ation to improve the model's likelihood. We log-odds as the natural parameter of the Bernoulli dis- evaluate the performance of logistic PCA|as tribution and the logistic function as its canonical link.
    [Show full text]
  • Linear, Ridge Regression, and Principal Component Analysis
    Linear, Ridge Regression, and Principal Component Analysis Linear, Ridge Regression, and Principal Component Analysis Jia Li Department of Statistics The Pennsylvania State University Email: [email protected] http://www.stat.psu.edu/∼jiali Jia Li http://www.stat.psu.edu/∼jiali Linear, Ridge Regression, and Principal Component Analysis Introduction to Regression I Input vector: X = (X1, X2, ..., Xp). I Output Y is real-valued. I Predict Y from X by f (X ) so that the expected loss function E(L(Y , f (X ))) is minimized. I Square loss: L(Y , f (X )) = (Y − f (X ))2 . I The optimal predictor ∗ 2 f (X ) = argminf (X )E(Y − f (X )) = E(Y | X ) . I The function E(Y | X ) is the regression function. Jia Li http://www.stat.psu.edu/∼jiali Linear, Ridge Regression, and Principal Component Analysis Example The number of active physicians in a Standard Metropolitan Statistical Area (SMSA), denoted by Y , is expected to be related to total population (X1, measured in thousands), land area (X2, measured in square miles), and total personal income (X3, measured in millions of dollars). Data are collected for 141 SMSAs, as shown in the following table. i : 1 2 3 ... 139 140 141 X1 9387 7031 7017 ... 233 232 231 X2 1348 4069 3719 ... 1011 813 654 X3 72100 52737 54542 ... 1337 1589 1148 Y 25627 15389 13326 ... 264 371 140 Goal: Predict Y from X1, X2, and X3. Jia Li http://www.stat.psu.edu/∼jiali Linear, Ridge Regression, and Principal Component Analysis Linear Methods I The linear regression model p X f (X ) = β0 + Xj βj .
    [Show full text]
  • Simple Linear Regression with Least Square Estimation: an Overview
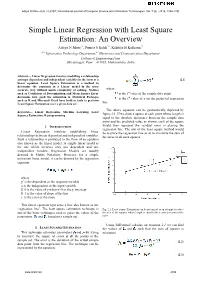
    Aditya N More et al, / (IJCSIT) International Journal of Computer Science and Information Technologies, Vol. 7 (6) , 2016, 2394-2396 Simple Linear Regression with Least Square Estimation: An Overview Aditya N More#1, Puneet S Kohli*2, Kshitija H Kulkarni#3 #1-2Information Technology Department,#3 Electronics and Communication Department College of Engineering Pune Shivajinagar, Pune – 411005, Maharashtra, India Abstract— Linear Regression involves modelling a relationship amongst dependent and independent variables in the form of a (2.1) linear equation. Least Square Estimation is a method to determine the constants in a Linear model in the most accurate way without much complexity of solving. Metrics where such as Coefficient of Determination and Mean Square Error is the ith value of the sample data point determine how good the estimation is. Statistical Packages is the ith value of y on the predicted regression such as R and Microsoft Excel have built in tools to perform Least Square Estimation over a given data set. line The above equation can be geometrically depicted by Keywords— Linear Regression, Machine Learning, Least Squares Estimation, R programming figure 2.1. If we draw a square at each point whose length is equal to the absolute difference between the sample data point and the predicted value as shown, each of the square would then represent the residual error in placing the I. INTRODUCTION regression line. The aim of the least square method would Linear Regression involves establishing linear be to place the regression line so as to minimize the sum of relationships between dependent and independent variables.
    [Show full text]
  • Principal Component Analysis (PCA) As a Statistical Tool for Identifying Key Indicators of Nuclear Power Plant Cable Insulation
    Iowa State University Capstones, Theses and Graduate Theses and Dissertations Dissertations 2017 Principal component analysis (PCA) as a statistical tool for identifying key indicators of nuclear power plant cable insulation degradation Chamila Chandima De Silva Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/etd Part of the Materials Science and Engineering Commons, Mechanics of Materials Commons, and the Statistics and Probability Commons Recommended Citation De Silva, Chamila Chandima, "Principal component analysis (PCA) as a statistical tool for identifying key indicators of nuclear power plant cable insulation degradation" (2017). Graduate Theses and Dissertations. 16120. https://lib.dr.iastate.edu/etd/16120 This Thesis is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Principal component analysis (PCA) as a statistical tool for identifying key indicators of nuclear power plant cable insulation degradation by Chamila C. De Silva A thesis submitted to the graduate faculty in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Major: Materials Science and Engineering Program of Study Committee: Nicola Bowler, Major Professor Richard LeSar Steve Martin The student author and the program of study committee are solely responsible for the content of this thesis. The Graduate College will ensure this thesis is globally accessible and will not permit alterations after a degree is conferred.
    [Show full text]
  • Generalized Linear Models
    CHAPTER 6 Generalized linear models 6.1 Introduction Generalized linear modeling is a framework for statistical analysis that includes linear and logistic regression as special cases. Linear regression directly predicts continuous data y from a linear predictor Xβ = β0 + X1β1 + + Xkβk.Logistic regression predicts Pr(y =1)forbinarydatafromalinearpredictorwithaninverse-··· logit transformation. A generalized linear model involves: 1. A data vector y =(y1,...,yn) 2. Predictors X and coefficients β,formingalinearpredictorXβ 1 3. A link function g,yieldingavectoroftransformeddataˆy = g− (Xβ)thatare used to model the data 4. A data distribution, p(y yˆ) | 5. Possibly other parameters, such as variances, overdispersions, and cutpoints, involved in the predictors, link function, and data distribution. The options in a generalized linear model are the transformation g and the data distribution p. In linear regression,thetransformationistheidentity(thatis,g(u) u)and • the data distribution is normal, with standard deviation σ estimated from≡ data. 1 1 In logistic regression,thetransformationistheinverse-logit,g− (u)=logit− (u) • (see Figure 5.2a on page 80) and the data distribution is defined by the proba- bility for binary data: Pr(y =1)=y ˆ. This chapter discusses several other classes of generalized linear model, which we list here for convenience: The Poisson model (Section 6.2) is used for count data; that is, where each • data point yi can equal 0, 1, 2, ....Theusualtransformationg used here is the logarithmic, so that g(u)=exp(u)transformsacontinuouslinearpredictorXiβ to a positivey ˆi.ThedatadistributionisPoisson. It is usually a good idea to add a parameter to this model to capture overdis- persion,thatis,variationinthedatabeyondwhatwouldbepredictedfromthe Poisson distribution alone.
    [Show full text]
  • Generalized Linear Models
    Generalized Linear Models Advanced Methods for Data Analysis (36-402/36-608) Spring 2014 1 Generalized linear models 1.1 Introduction: two regressions • So far we've seen two canonical settings for regression. Let X 2 Rp be a vector of predictors. In linear regression, we observe Y 2 R, and assume a linear model: T E(Y jX) = β X; for some coefficients β 2 Rp. In logistic regression, we observe Y 2 f0; 1g, and we assume a logistic model (Y = 1jX) log P = βT X: 1 − P(Y = 1jX) • What's the similarity here? Note that in the logistic regression setting, P(Y = 1jX) = E(Y jX). Therefore, in both settings, we are assuming that a transformation of the conditional expec- tation E(Y jX) is a linear function of X, i.e., T g E(Y jX) = β X; for some function g. In linear regression, this transformation was the identity transformation g(u) = u; in logistic regression, it was the logit transformation g(u) = log(u=(1 − u)) • Different transformations might be appropriate for different types of data. E.g., the identity transformation g(u) = u is not really appropriate for logistic regression (why?), and the logit transformation g(u) = log(u=(1 − u)) not appropriate for linear regression (why?), but each is appropriate in their own intended domain • For a third data type, it is entirely possible that transformation neither is really appropriate. What to do then? We think of another transformation g that is in fact appropriate, and this is the basic idea behind a generalized linear model 1.2 Generalized linear models • Given predictors X 2 Rp and an outcome Y , a generalized linear model is defined by three components: a random component, that specifies a distribution for Y jX; a systematic compo- nent, that relates a parameter η to the predictors X; and a link function, that connects the random and systematic components • The random component specifies a distribution for the outcome variable (conditional on X).
    [Show full text]
  • Time-Series Regression and Generalized Least Squares in R*
    Time-Series Regression and Generalized Least Squares in R* An Appendix to An R Companion to Applied Regression, third edition John Fox & Sanford Weisberg last revision: 2018-09-26 Abstract Generalized least-squares (GLS) regression extends ordinary least-squares (OLS) estimation of the normal linear model by providing for possibly unequal error variances and for correlations between different errors. A common application of GLS estimation is to time-series regression, in which it is generally implausible to assume that errors are independent. This appendix to Fox and Weisberg (2019) briefly reviews GLS estimation and demonstrates its application to time-series data using the gls() function in the nlme package, which is part of the standard R distribution. 1 Generalized Least Squares In the standard linear model (for example, in Chapter 4 of the R Companion), E(yjX) = Xβ or, equivalently y = Xβ + " where y is the n×1 response vector; X is an n×k +1 model matrix, typically with an initial column of 1s for the regression constant; β is a k + 1 ×1 vector of regression coefficients to estimate; and " is 2 an n×1 vector of errors. Assuming that " ∼ Nn(0; σ In), or at least that the errors are uncorrelated and equally variable, leads to the familiar ordinary-least-squares (OLS) estimator of β, 0 −1 0 bOLS = (X X) X y with covariance matrix 2 0 −1 Var(bOLS) = σ (X X) More generally, we can assume that " ∼ Nn(0; Σ), where the error covariance matrix Σ is sym- metric and positive-definite. Different diagonal entries in Σ error variances that are not necessarily all equal, while nonzero off-diagonal entries correspond to correlated errors.
    [Show full text]
  • Simple Linear Regression: Straight Line Regression Between an Outcome Variable (Y ) and a Single Explanatory Or Predictor Variable (X)
    1 Introduction to Regression \Regression" is a generic term for statistical methods that attempt to fit a model to data, in order to quantify the relationship between the dependent (outcome) variable and the predictor (independent) variable(s). Assuming it fits the data reasonable well, the estimated model may then be used either to merely describe the relationship between the two groups of variables (explanatory), or to predict new values (prediction). There are many types of regression models, here are a few most common to epidemiology: Simple Linear Regression: Straight line regression between an outcome variable (Y ) and a single explanatory or predictor variable (X). E(Y ) = α + β × X Multiple Linear Regression: Same as Simple Linear Regression, but now with possibly multiple explanatory or predictor variables. E(Y ) = α + β1 × X1 + β2 × X2 + β3 × X3 + ::: A special case is polynomial regression. 2 3 E(Y ) = α + β1 × X + β2 × X + β3 × X + ::: Generalized Linear Model: Same as Multiple Linear Regression, but with a possibly transformed Y variable. This introduces considerable flexibil- ity, as non-linear and non-normal situations can be easily handled. G(E(Y )) = α + β1 × X1 + β2 × X2 + β3 × X3 + ::: In general, the transformation function G(Y ) can take any form, but a few forms are especially common: • Taking G(Y ) = logit(Y ) describes a logistic regression model: E(Y ) log( ) = α + β × X + β × X + β × X + ::: 1 − E(Y ) 1 1 2 2 3 3 2 • Taking G(Y ) = log(Y ) is also very common, leading to Poisson regression for count data, and other so called \log-linear" models.
    [Show full text]
  • Lecture 18: Regression in Practice
    Regression in Practice Regression in Practice ● Regression Errors ● Regression Diagnostics ● Data Transformations Regression Errors Ice Cream Sales vs. Temperature Image source Linear Regression in R > summary(lm(sales ~ temp)) Call: lm(formula = sales ~ temp) Residuals: Min 1Q Median 3Q Max -74.467 -17.359 3.085 23.180 42.040 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -122.988 54.761 -2.246 0.0513 . temp 28.427 2.816 10.096 3.31e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 35.07 on 9 degrees of freedom Multiple R-squared: 0.9189, Adjusted R-squared: 0.9098 F-statistic: 101.9 on 1 and 9 DF, p-value: 3.306e-06 Some Goodness-of-fit Statistics ● Residual standard error ● R2 and adjusted R2 ● F statistic Anatomy of Regression Errors Image Source Residual Standard Error ● A residual is a difference between a fitted value and an observed value. ● The total residual error (RSS) is the sum of the squared residuals. ○ Intuitively, RSS is the error that the model does not explain. ● It is a measure of how far the data are from the regression line (i.e., the model), on average, expressed in the units of the dependent variable. ● The standard error of the residuals is roughly the square root of the average residual error (RSS / n). ○ Technically, it’s not √(RSS / n), it’s √(RSS / (n - 2)); it’s adjusted by degrees of freedom. R2: Coefficient of Determination ● R2 = ESS / TSS ● Interpretations: ○ The proportion of the variance in the dependent variable that the model explains.
    [Show full text]
  • Chapter 2 Simple Linear Regression Analysis the Simple
    Chapter 2 Simple Linear Regression Analysis The simple linear regression model We consider the modelling between the dependent and one independent variable. When there is only one independent variable in the linear regression model, the model is generally termed as a simple linear regression model. When there are more than one independent variables in the model, then the linear model is termed as the multiple linear regression model. The linear model Consider a simple linear regression model yX01 where y is termed as the dependent or study variable and X is termed as the independent or explanatory variable. The terms 0 and 1 are the parameters of the model. The parameter 0 is termed as an intercept term, and the parameter 1 is termed as the slope parameter. These parameters are usually called as regression coefficients. The unobservable error component accounts for the failure of data to lie on the straight line and represents the difference between the true and observed realization of y . There can be several reasons for such difference, e.g., the effect of all deleted variables in the model, variables may be qualitative, inherent randomness in the observations etc. We assume that is observed as independent and identically distributed random variable with mean zero and constant variance 2 . Later, we will additionally assume that is normally distributed. The independent variables are viewed as controlled by the experimenter, so it is considered as non-stochastic whereas y is viewed as a random variable with Ey()01 X and Var() y 2 . Sometimes X can also be a random variable.
    [Show full text]
  • Week 7: Multiple Regression
    Week 7: Multiple Regression Brandon Stewart1 Princeton October 24, 26, 2016 1These slides are heavily influenced by Matt Blackwell, Adam Glynn, Jens Hainmueller and Danny Hidalgo. Stewart (Princeton) Week 7: Multiple Regression October 24, 26, 2016 1 / 145 Where We've Been and Where We're Going... Last Week I regression with two variables I omitted variables, multicollinearity, interactions This Week I Monday: F matrix form of linear regression I Wednesday: F hypothesis tests Next Week I break! I then ::: regression in social science Long Run I probability ! inference ! regression Questions? Stewart (Princeton) Week 7: Multiple Regression October 24, 26, 2016 2 / 145 1 Matrix Algebra Refresher 2 OLS in matrix form 3 OLS inference in matrix form 4 Inference via the Bootstrap 5 Some Technical Details 6 Fun With Weights 7 Appendix 8 Testing Hypotheses about Individual Coefficients 9 Testing Linear Hypotheses: A Simple Case 10 Testing Joint Significance 11 Testing Linear Hypotheses: The General Case 12 Fun With(out) Weights Stewart (Princeton) Week 7: Multiple Regression October 24, 26, 2016 3 / 145 Why Matrices and Vectors? Here's one way to write the full multiple regression model: yi = β0 + xi1β1 + xi2β2 + ··· + xiK βK + ui Notation is going to get needlessly messy as we add variables Matrices are clean, but they are like a foreign language You need to build intuitions over a long period of time (and they will return in Soc504) Reminder of Parameter Interpretation: β1 is the effect of a one-unit change in xi1 conditional on all other xik . We are going to review the key points quite quickly just to refresh the basics.
    [Show full text]
  • 1 Simple Linear Regression I – Least Squares Estimation
    1 Simple Linear Regression I – Least Squares Estimation Textbook Sections: 18.1–18.3 Previously, we have worked with a random variable x that comes from a population that is normally distributed with mean µ and variance σ2. We have seen that we can write x in terms of µ and a random error component ε, that is, x = µ + ε. For the time being, we are going to change our notation for our random variable from x to y. So, we now write y = µ + ε. We will now find it useful to call the random variable y a dependent or response variable. Many times, the response variable of interest may be related to the value(s) of one or more known or controllable independent or predictor variables. Consider the following situations: LR1 A college recruiter would like to be able to predict a potential incoming student’s first–year GPA (y) based on known information concerning high school GPA (x1) and college entrance examination score (x2). She feels that the student’s first–year GPA will be related to the values of these two known variables. LR2 A marketer is interested in the effect of changing shelf height (x1) and shelf width (x2)on the weekly sales (y) of her brand of laundry detergent in a grocery store. LR3 A psychologist is interested in testing whether the amount of time to become proficient in a foreign language (y) is related to the child’s age (x). In each case we have at least one variable that is known (in some cases it is controllable), and a response variable that is a random variable.
    [Show full text]