Flood Frequency Analysis of Tel Basin of Mahanadi River System, India Using Annual Maximum and POT Flood Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

PANCHAYAT SAMITI, KESINGA Letter No.335 Date.01.02.2019
PANCHAYAT SAMITI, KESINGA Letter No.335 Date.01.02.2019 TENDER CALL NOTICE NO Sealed tenders in single cover system are invited from manufacturer/suppliers of Solar PV System Stand Alone street lighting system having valid test certificates from MNRE authorized test centers for their products, GST certificate, PAN Card, other relevant documents for supply, installation, commissioning and maintenance of Integrated Solar Street Lighting System-17 Watt LED Lamp including all accessories with five years warranty & five years CMC in different Gram Panchayats of Utkela Rurban cluster in the district of Kalahandi duly self attesting all the pages.The intended bidders need to submit the bids separately for each Gram Panchayat as mentioned below. For details, please visit to the district web site www.kalahandi.nic.in or BDO, Panchayat Samiti, Kesinga. Estimated EMD Cost of bid Sl. Name of the Completion Item cost (Rs. (Rs. in document (Rs. No. GP period in Lakh) Lakh) in Thousand) Utkela 3 Calendar 01. 49.63 0.496 6.00 Integrated Solar (Part-A) months Street Lighting Utkela 3 Calendar 02. 28.37 0.284 6.00 System - 17 (Part-B) months Watt LED Lamp 3 Calendar 03. including all Kikia 46.8 0.468 6.00 months accessories with 3 Calendar 04. five years Gokuleswar 27.6 0.276 6.00 months warranty & five 3 Calendar 05. years CMC. Chancher 46.8 0.468 6.00 months The bid documents can be obtained from the district web site www.kalahandi.nic.in or BDO, Panchayat Samiti, Kesinga from 1st to 10th Feb. -

Brief Industrial Profile of Kalahandi District
Contents S. No. Topic Page No. 1. General Characteristics of the District 3 1.1 Location & Geographical Area 3 1.2 Topography 3 1.3 Availability of Minerals. 4 1.4 Forest 5 1.5 Administrative set up 5 2. District at a glance 6 2.1 Existing Status of Industrial Area in the District of Kalahandi 9 3. Industrial Scenario Of Kalahandi 10 3.1 Industry at a Glance 9 3.2 Year Wise Trend Of Units Registered 11 3.3 Details Of Existing Micro & Small Enterprises & Artisan Units In The 10 District 3.4 Large Scale Industries / Public Sector undertakings 11 3.5 Major Exportable Item 12 3.6 Growth Trend 12 3.7 Vendorisation / Ancillarisation of the Industry 12 3.8 Medium Scale Enterprises 12 3.8.1 List of the units in Kalahandi & near by Area 11 3.8.2 Major Exportable Item 12 3.9 Service Enterprises 12 3.9.1 Potentials areas for service industry 13 3.10 Potential for new MSMEs 13 4. Existing Clusters of Micro & Small Enterprise 14 4.1 Detail Of Major Clusters 14 4.1.1 Manufacturing Sector 14 4.1.2 Service Sector 14 4.2 Details of Identified cluster 14 5. General issues raised by industry association during the course of 14 meeting 6 Steps to set up MSMEs 15 2 Brief Industrial Profile of Kalahandi District 1. General Characteristics of the District The present district of Kalahandi was in ancient times a part of South Kosala. It was a princely state. After independence of the country, merger of princely states took place on 1st January, 1948. -

Pollution Mapping with Reference to Transmission System in Eastern Region 1
POLLUTION MAPPING WITH REFERENCE TO TRANSMISSION SYSTEM IN EASTERN REGION 1. Introduction Electricity, in the 21st century, plays a significant role in the socio-economic development of any country. With rapid advancement in the industrial sector and urbanization, per capita electrical energy consumption becomes a unit of measurement for the development of a country. Countries worldwide move for electrification all over its terrain. In order to have a reliable power supply, it is necessary to have a proper coordination between generation, transmission and distribution systems [1-3]. In general, the generating stations are located near the available energy resources. The transmission systems provide a bulk transportation path for the efficient transfer of electrical power from the generating station to the load centres with the larger geographical area. Distribution system distributes the electrical power from the load centre to the consumers with the smaller geographical area. In order to electrify load centres located at the larger distance and to transfer electrical power in an efficient manner, it becomes necessary to have a higher system voltage in the transmission network. Utilities all over the world are moving towards higher transmission voltages in their power lines and the system voltage up to 1200 kV has been adopted quite recently [4-5]. 2. The Pollution Problem Porcelain insulators play many vital roles in the power system such as bearing suspension and tension loads in the transmission line, as a supporting structure in substations, providing an optimal electrical insulation as indoor and outdoor insulators, provides the proper housing and grounding for live conductor by serving as bushings etc., Outdoor insulators, as the name suggests, are exposed to both man-made and natural pollution throughout their operation. -

2011-Dshb-Kalahandi.Pdf
GOVERNMENT OF ODISHA DISTRICT STATISTICAL HANDBOOK KALAHANDI 2011 DISTRICT PLANNING AND MONITORING UNIT KALAHANDI ( Price : Rs.25.00 ) CONTENTS Table No. SUBJECT PAGE ( 1 ) ( 2 ) ( 3 ) Socio-Economic Profile : Kalahandi … 1 Administrative set up … 4 I POSITION OF DISTRICT IN THE STATE 1.01 Geographical Area … 5 District wise Population with Rural & Urban and their proportion of 1.02 … 6 Odisha. District-wise SC & ST Population with percentage to total population of 1.03 … 8 Odisha. 1.04 Population by Sex, Density & Growth rate … 10 1.05 District wise sex ratio among all category, SC & ST by residence of Odisha. … 11 1.06 District wise Literacy rate, 2011 Census … 12 Child population in the age Group 0-6 in different district of Odisha. 1.07 … 13 II AREA AND POPULATION Geographical Area, Households and Number of Census Villages in different 2.01 … 14 Blocks and ULBs of the District. 2.02 Classification of workers (Main+ Marginal) … 15 2.03 Total workers and work participation by residence … 17 III CLIMATE 3.01 Month wise Actual Rainfall in different Rain gauge Stations in the District. … 18 3.02 Month wise Temperature and Relative Humidity of the district. … 20 IV AGRICULTURE 4.01 Block wise Land Utilisation pattern of the district. … 21 Season wise Estimated Area, Yield rate and Production of Paddy in 4.02 … 23 different Blocks and ULBs of the district. Estimated Area, Yield rate and Production of different Major crops in the 4.03 … 25 district. 4.04 Source- wise Irrigation Potential Created in different Blocks of the district … 26 Achievement of Pani Panchayat programme of different Blocks of the 4.05 … 27 district 4.06 Consumption of Chemical Fertiliser in different Blocks of the district. -

Kalahandi Family Planning Plan 2011 12
DRAFT 2011 -12 District Family Planning Plan District: KALAHANDI District Family Welfare Bureau Zilla Swasthya Samiti KALAHANDI DISTRICT FAMILY PLANNING PLAN 2011 -12 1 KALAHANDI DISTRICT FAMILY PLANNING PLAN 2011-12 2 KALAHANDI DISTRICT FAMILY PLANNING PLAN 2011-12 3 Table of Contents Chapter Topics Chapter – 1 Background Chapter – 2 Situational Analyses a. Contraceptive Use b. Service Delivery c. Quality Assurance Mechanism d. Logistic and Supply System e. Human Resource Development f. Communication Activities g. Private Sector Partnership h. Monitoring and Evaluation Chapter – 3 District Priorities as per the situations with respect to the State mandate. Chapter – 4 Family Planning Plan for the year 2011-12 a. Service Delivery b. Human Resource Development & Training c. Logistics and supply chain with requirement & distribution plan d. Communication Activities e. Private Sector Partnership f. Monitoring and Evaluation g. Any other (Innovations, Dist/Block/Sector specific) IEC, new plans etc. Chapter – 5 Resource Requirements KALAHANDI DISTRICT FAMILY PLANNING PLAN 2011-12 4 Executive Summary – Kalahandi district is situated in the southwestern portion of Orissa. Geographically this district lies between 19º 8’ N 20º 25’ N latitudes and 82 0 32 ’ E and 83 0 47’ E longitudes with geographical area of 7920 sq Km. The population of the Kalahandi district as per the 2011 census is 157305; the sex ratio is 1003 per one thousand male. It has 13 blocks, 273 Grampanchayats, 2236 Rev villages (including 137 uninhabited villages), 13 Tahsils, and 2 Subdivisions. It has 4 towns Bhawanipatna Municipality, Junagarh & Kesinga NAC and Dharamgarh. Out of 13 blocks two are Tribal blocks1-Biswanathpur 2.Thuamulrampur. -

List of Candidates ( Kalahandi) for Document
LIST OF CANDIDATES ( KALAHANDI) FOR DOCUMENT VERIFICATION & CBST THE POST OF ANM-MHU (ADVT NO 4288/21.08.2018) UNDER NHM, KALAHANDI (VENUE-ANMTC, BHAWANIPATNA) CASTE DATE OF SL. APPL. NAME OF THE FATHER'S/ DOMICILE SEX (UR/SC/ DOB DOCUMENT PRESENT ADDRESS NO. NO. CANDIDATE HUSBAND'S NAME DISTRICT (M/F) ST/SEBC/ (DD-MM-YYYY) VERIFICATION SEBC) & CBST UR-CATEGORY AT- TUJUNG, PO- M.RAMPUR, KALAHANDI, 1 559 PRATIMA NAG BRUNDABAN NAG KALAHANDI F SC 20/10/1993 15-Dec-18 766102 AT-DEWANSAHEB PADA, PO- 2 679 NILEEMA BHATI JAGADISH BHATI BHAWANIPATNA, DIST-KALAHANDI, PIN- KALAHANDI F SEBC 15/05/1995 15-Dec-18 766001 AT-GHUGURBAHALI,PO-SANTPUR,VIA- 3 8 ASHA LATA SAHU TIKARAM SAHU KALAHANDI F SEBC 01/05/1997 15-Dec-18 NARLA, KALAHANDI-766110 AT/PO-BRUNDABAHAL,VIA- 4 269 LILI RAUT RAHASA RAUT KALAHANDI F SEBC 10/18/1992 15-Dec-18 GOLAMUNDA,DIST-KALAHANDI,PIN-766016 AT- KANTAMAL, PO- KUHURA, VIA- BORDA, 5 650 HEMALATA SAHU SANYASI SAHU KEGAON, GOLAMUNDA, KALAHANDI, KALAHANDI F SEBC 24/11/1995 15-Dec-18 766036 AT- LIMSER, PO- BRUNDABAHAL, VIA- 6 82 LILABATI MEHER GUNAKARA MEHER GOLAMUNDA, DIST- KALAHANDI, PIN- KALAHANDI F SEBC 5/16/1996 15-Dec-18 766016 AT- LAKHAGUDA, PO- RUPRARPAD, PS- 7 552 SEEMA BHOI BASANTA BHOI KALAHANDI F SEBC 01/05/1995 15-Dec-18 NARLA, KALAHANDI, 766101 AT/PO- NAKTIKANI, VIA- GOLAMUNDA, DIST- 8 432 KAMINI SENAPATI PREM SENAPATI KALAHANDI F SEBC 11/07/1991 15-Dec-18 KALAHANDI, PIN- 766016 PRAKASH CH. AT/PO-JUNAGARH,TALABANDHAPADA ,DIST- 9 344 MANISHA GHADEI KALAHANDI F SEBC 03/11/1994 15-Dec-18 GHADEI KALAHANDI-766014 AT/PO- -
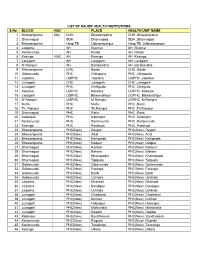
LIST of MAJOR HEALTH INSTITUTIONS S.No BLOCK NAC
LIST OF MAJOR HEALTH INSTITUTIONS S.No BLOCK NAC PLACE HEALTH UNIT NAME 1 Bhawanipatna Mty DHH Bhawanipatna DHH ,Bhawanipatna 2 Dharmagad SDH Dharmagad SDH ,Dharmagad 3 Bhawanipatna Hosp TB Uditnarayanpur Hosp TB ,Uditnarayanpur 4 Jaipatna AH Ranmal AH ,Ranmal 5 Karlamunda AH Risida AH ,Risida 6 Kesinga NAC AH Kesinga AH ,Kesinga 7 Lanjigarh AH Lanjigarh AH ,Lanjigarh 8 M Rampur AH Barabandha AH ,Barabandha 9 Bhawanipatna CHC Borda CHC ,Borda 10 Golamunda PHC Chhapuria PHC ,Chhapuria 11 Jaipatna UGPHC Jaipatna UGPHC ,Jaipatna 12 Junagarh CHC Junagarh CHC ,Junagarh 13 Junagarh PHC Chilliguda PHC ,Chiliguda 14 Koksara UGPHC Koksara UGPHC ,Koksara 15 Lanjigarh UGPHC Biswanathpur UGPHC ,Biswanathpur 16 M Rampur UGPHC M.Rampur UGPHC ,M.Rampur 17 Narla PHC Narla PHC ,Narla 18 Th. Rampur PHC Th.Rampur PHC ,Th.Rampur 19 Dharmagad PHC Parla PHC ,Parla 20 Kalampur PHC Kalampur PHC ,Kalampur 21 Karlamunda PHC Karlamunda PHC ,Karlamunda 22 Kesinga PHC Pastikudi PHC ,Pastikudi 23 Bhawanipatna PHC(New) Deypur PHC(New) ,Deypur 24 Bhawanipatna PHC(New) Artal PHC(New) ,Artal 25 Bhawanipatna PHC(New) Karlapada PHC(New) ,Karlapada 26 Bhawanipatna PHC(New) Dadpur PHC(New) ,Dadpur 27 Dharmagad PHC(New) Kankeri PHC(New) ,Kankeri 28 Dharmagad PHC(New) Behera PHC(New) ,Behera 29 Dharmagad PHC(New) Khairapadar PHC(New) ,Khairapadar 30 Dharmagad PHC(New) Tipiguda PHC(New) ,Tipiguda 31 Golamunda PHC(New) Golamunda PHC(New) ,Golamunda 32 Golamunda PHC(New) Faranga PHC(New) ,Faranga 33 Golamunda PHC(New) Bordi PHC(New) ,Bordi 34 Golamunda PHC(New) Uchhala PHC(New) -

M.I.Division Kalahandi.Xlsx
STATUS OF IRRIGATION SUPPLIED DURING KHARIFF AS ON SEPTEMBER 2015 IN KALAHANDI DISTRICT Length of canal system in Ayacut in Ha. Reason for less/ Km excess of ayacut Sl Name of Ayacut Name of Block Name of MIP Actual length in Actual irrigated/ Reason No. District Design Designed irrigated upto which water Potential for not reaching length Ayacut 30th Sept' supplied Created tail end 2015 1 2 3 4 5 6 7 8 9 10 1 Kalahandi Bhawanipatna Artal MIP 2.21 1.75 81.00 81.00 65.00 Shortage of Water 2 Kalahandi Bhawanipatna Ashasagar MIP 2.50 2.50 121.00 121.00 50.00 Shortage of Water 3 Kalahandi Bhawanipatna Balipati MIP 1.00 1.00 40.00 40.00 40.00 Full Ayacut 4 Kalahandi Bhawanipatna Devisagar MIP 4.60 4.05 132.00 132.00 95.00 Shortage of Water 5 Kalahandi Bhawanipatna Haldi MIP 1.10 0.85 49.00 49.00 40.00 Shortage of Water 6 Kalahandi Bhawanipatna Jamunasagar MIP 4.31 3.80 180.00 180.00 160.00 Shortage of Water 7 Kalahandi Bhawanipatna Karlapada MIP 0.83 0.83 40.00 40.00 40.00 Full Ayacut 8 Kalahandi Bhawanipatna Kasakendu MIP 0.70 0.50 40.00 40.00 30.00 Shortage of Water Kharsanpur MIP 9 Kalahandi Bhawanipatna 0.55 0.40 49.00 49.00 35.00 Shortage of Water (D/W) 10 Kalahandi Bhawanipatna Kusumsila MIP 0.98 0.98 114.00 114.00 90.00 Shortage of Water Mahijore MIP 11 Kalahandi Bhawanipatna 1.08 0.85 67.00 67.00 40.00 Shortage of Water (D/W) Medinipur MIP 12 Kalahandi Bhawanipatna 5.41 4.25 396.00 396.00 240.00 Shortage of Water (D/W) 13 Kalahandi Bhawanipatna Pipalnalla MIP 14.00 13.20 809.00 809.00 750.00 Shortage of Water 14 Kalahandi Bhawanipatna -
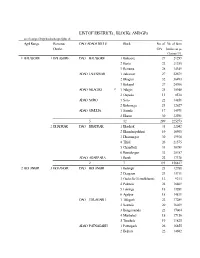
LIST of Districts, Blocks and Gps User1/Compcell/Mpr/Databank/Apr-Gplist Sh
LIST OF DISTRICTs, BLOCKs AND GPs user1/compcell/mpr/databank/apr-Gplist sh. Agril Range Revenue DAO/ ADAO CIRCLE Block No. of No. of farm District GPs families as per Census '91 1 BALASORE 1 BALASORE DAO BALASORE 1 Balasore 27 21299 2 Basta 22 21255 3 Remuna 28 14349 ADAO JALESWAR 1 Jaleswar 27 22679 2 Bhograi 32 36493 3 Baliapal 27 24700 ADAO NILAGIRI * 1 Nilagiri 25 10948 2 Oupada 11 8510 ADAO SORO 1 Soro 22 14851 2 Bahanaga 21 12627 ADAO SIMULIA 1 Simulia 17 14971 2 Khaira 30 22591 5 12 289 225273 2 BHADRAK DAO BHADRAK 1 Bhadrak 31 22042 2 Bhandaripokhari 19 16900 3 Dhamnagar 30 19936 4 Tihidi 26 21575 5 Chandbali 33 30799 6 Basudevpur 32 28187 ADAO AGARPARA 1 Bonth 22 17378 2 7 193 156817 2 BOLANGIR 3 BOLANGIR DAO BOLANGIR 1 Bolangir 23 12780 2 Deogaon 23 13711 3 Gudvella (Tentulikhunti) 12 9213 4 Puintala 24 16409 5 Loisinga 18 13281 6 Agalpur 18 14811 DAO TITLAGARH 1 Titlagarh 22 17289 2 Saintala 20 16029 3 Bangamunda 22 17004 4 Muribahal 18 17156 5 Tureikela 19 11825 ADAO PATNAGARH 1 Patnagarh 26 16855 2 Belpara 22 14682 3 Khaprakhol 18 15343 3 14 285 206388 4 SONEPUR DAO SONEPUR 1 Sonepur 13 10422 2 Tarva 18 11032 ADAO BIRMAHARAJPUR 1 Biramaharajpur 13 13968 2 Ullunda 16 11756 ADAO DUNGRIPALI 1 Dunguripalli 21 19477 2 Binka 15 15104 3 6 96 81759 3 CUTTACK 5 CUTTACK DAO CUTTACK 1 Cuttack 21 6976 2 Barang 16 4824 3 Niali 23 17916 4 Kantapada 14 8153 ADAO SALIPUR 1 Salipur 32 11669 2 Nischintakoili 40 15184 3 Mahanga 34 19207 4 Tangi-Choudwar 20 11840 DAO ATHGARH 1 Athgarh 29 14011 2 Tigiria 10 6482 3 Badamba 36 15323 4 Narsinghpur -

District Census Handbook, Kalahandi, Orissa
CENSUS OF INDIA, 1961 ORISSA DISTRICT CENSUS HANDBOOK KALAHANDI - M. AHMED, I.A.B. Superintendent of Census Operations Orissa CENSUS -OF INDIA, 1961 DISTRICT CENSUS HANDBOOK KALAHANDI PRINTED AND PUBLISHED BY SUPERINTENDENT. ORISSA GOVERNMENT PRESS CUTTACK, 1965 RAJBHAVAN BHUBANESWAR Tfl!,_9t1!;Augl.lst, 1965 GOVERNOR, ORISSA FOREWORD THE State of Orissa represents 4·9 per cent of the area and 4·02 per cent ;'f th~ p(;pul:tion of India. Nature has been generous in providing the State with untold wealth in minerals, :water, fertile land and forests. The rich alluvial soil in the deltaic areas as well as along the river basins, as also most of the uplands, are capable of producing a large variety of crops. The water-shed areas of the major rivers and hill tracts are covered with vast forests of great economic value. The State has roughly half the mineral wealth of India hidden underground awaiting exploitation. Vast quantities of water flow down the rivers which, fortunately for Orissa, are strategically dispersed over the entire State, and, if harnessed properly, will banish the twin spectre of floods and droughts haunting vast areas of culturable lands, and at the same time provide water for irrigating millions of acres in the coastal areas and upland and for generating large quantities of hydro-electric power for use in industry, and also make available hundreds of miles of irrigation-cum-navigation waterways for inland transport, and large areas for fish culture, recreation and tourism. These bounties of nature, the variety of picturesque landscapes and the long seacoast have attracted people from different parts of the country so that through the centuries a fine blend of human material and culture has developed. -

Kalahandi District
Govt. of India MINISTRY OF WATER RESOURCES CENTRAL GROUND WATER BOARD OF KALAHANDI DISTRICT SOUTH EASTERN REGION BHUBANESWAR MAY, 2013 1 KALAHANDI DISTRICT AT A GLANCE Sl ITEMS Statistics No 1. GENERAL INFORMATION i. Geographical Area (Sq. Km.) 7920 ii. Administrative Divisions as on 31.03.2011 Number of Tehsil / Block 7 Tehsils, 13 Blocks Number of Panchayat / Villages 273 Panchayats 2099- Inhabited Villages, 137-Inhabited Villages, iii Population (As on 2011 Census) 13,35,494 iv Average Annual Rainfall (mm) 1378.2 2. GEOMORPHOLOGY Major physiographic units Gently undulating terrain, Isolated Mounds & Hills Major Drainages Indra, Udanti, Hatti, Sagada, Jonk 3. LAND USE (Sq. Km.) a) Forest Area 64271 b) Net Sown Area 290901 c) Cultivable Area 4. MAJOR SOIL TYPES Inceptisols, Alfisols, Vertisols, Histosols, Entisols 5. AREA UNDER PRINCIPAL CROPS Paddy 265642Ha, Pulses etc. 16892 Ha, Oilseeds 4976 Ha 6. IRRIGATION BY DIFFERENT SOURCES (Areas and Number of Structures) Dugwells, Tube wells / Borewells 28968Ha, Major/Medium Irrigation Projects 62,814 Ha (Kharif)27,993 Ha (Rabi) Minor Irrigation Projects 21579 Ha (Kharif)3880 Ha (Rabi) Minor Irrigation Projects(Lift) 8660 Ha (Kharif)5196 Ha (Rabi) Other sources 829Ha Net irrigated area 159919 Ha Gross irrigated area 188058 Ha 7. NUMBERS OF GROUND WATER MONITORING WELLS OF CGWB ( As on 31-3-2011) No of Dugwells 54 No of Piezometers 4 10. PREDOMINANT GEOLOGICAL Granites, Granite Gneiss & its variants, FORMATIONS Khondalite, 11. HYDROGEOLOGY Major Water bearing formation 1.3 – 9.4 mbgl Pre-monsoon Depth to water level during 2011 Post-monsoon Depth to water level during 0.84 – 4.47 mbgl 2011 Long term water level trend in 10 yrs (2001- Pre-monsoon 63.04 % show rising and 36.96% 2011) in m/yr show declining trend. -
NAME of ELECTED CHAIRMAN and VICE CHAIRMAN Sl
24 NAME OF ELECTED CHAIRMAN AND VICE CHAIRMAN Sl. Name of the Sl. Name of Panchayat Elected Chairman Elected Vice Chairman NO District NO Samiti 1 Angul 1 Angul Niranjan Dehuri Mamata Pradhan 2 Athamalik Minakshee Dalei Babita Karna 3 Kaniha Namita Sahu Tripurari Pradhan 4 Kishorenagar Babita Pradhan Sunil Kumar Pradhan 5 Chendipada Ashok Kumar Pradhan Susama Roul 6 Talcher Brundaban Behera Subarna Sahu 7 Pallahara Mukesh Kumar Pal Lili Pradhan 8 Banarpal Anjali Bhoi Prasanta Kumar Behera 2 Bolangir 1 Agalpur Sunita Majhi Man Mohan Patel 2 Khaprakhol Purnamasi Bariha Prakash Chandra Mehera 3 Gudvela Ashok Chandra Dora Nalini Seth 4 Titilagarh Ramakanti Putel Bhudhara Majhi 5 Turekela Anu Bhue Naukeshi Sipka 6 Deogaon Reena Meher Raju Bag 7 Patnagarh Bhaktabandhu Naik Padmini Sahu 8 Puintala Jamuna Biswal Raghunath Gurandi 9 Bangomunda Ranjubala Behera Mamraj Jain 10 Balangir Golap Bag Jasobanti Baghar 11 Muribahal Hansraj Jain Sundamati Bag 12 Saintala Ahalya Mallik Pramod Kumar Bhoi 13 Loisingha Kanti Seth Jatindra Kumar Patel 3 Balasore 1 Simulia Dharitri Maharana Gouranga Chandra Patri 2 Balasore Narayan Pradhan Supriti Giri 3 Nilgiri Janaki Singh Ramesh Ch. Mohanty 4 Bahanaga Saraswati Mohallik Sanjay Kumar Nayak 5 Khaira Abhilipsa Sahu Jayanta Kumar Rout 6 Soro Attashi Mohapatra Ratikanta Mohanty 7 Jaleswar Sabita Rani Dalei Brajamohan Pradhan 8 Oupada Nirmala Biswal Tilottama Parida 9 Baliapal Bijan Nayak Kabita Das 10 Remuna Sushant Pattnayak Manjulata Das 11 Basta Laxmidhara Das Ranjana Das 12 Bhograi Manju Rani Behera Deepak